A rectangle has a length of 2 miles and a width of 6 miles. What is the area in square kilometers? Round your answer to theHow many liters of paint are in a 5-gallon bucket? Round your answer to the nearest liter.
Answers
The area of a rectangle is the total space it would cover in a two-dimensional plane. Thus, the required answers are:
i. The area of the rectangle is 31.1 \(km^{2}\).
ii. There are 18.9 liters of paint in the 5-gallon bucket.
Plane figures are bounded by straight sides. Thus examples are triangle, rectangle, square, trapezium, rhombus, etc.
A rectangle is a plane shape that has four sides. In this figure, two opposite sides have equal lengths.
The area of a rectangle = length x width
So in the given question, we have:
1) 1 mile = 1.60934 Kilometres
Thus;
2 miles = 3.21869 km
6 miles = 9.65606 km
Area of the given rectangle = 3.21869 x 9.65606
= 31.0799
The area of the rectangle is 31.1 \(km^{2}\).
2) Given a 5-gallon bucket, then:
1 gallon = 3.78541 liters
So that;
5 gallons = 18.9271 liters
= 18.9 liters
Thus there are 18.9 liters of paint in the 5-gallon bucket.
For more clarifications on the area of a rectangle, visit: https://brainly.com/question/20968176
#SPJ1
Related Questions
Order cube root of eighty-eight, twenty-eight ninths, square root of nineteen from greatest to least.
cube root of eighty-eight, twenty-eight ninths, square root of nineteen
twenty-eight ninths, square root of nineteen, cube root of eighty-eight
twenty-eight ninths, cube root of eighty-eight, square root of nineteen
cube root of eighty-eight, square root of nineteen, twenty-eight ninths
Answers
Answer:
(a) twenty-eight ninths, square root of nineteen, cube root of eighty-eight
Step-by-step explanation:
When ordering a list of numbers by hand, it is convenient to convert them to the same form. Decimal equivalents are easily found using a calculator.
OrderThe attachment shows the ordering, least to greatest, to be ...
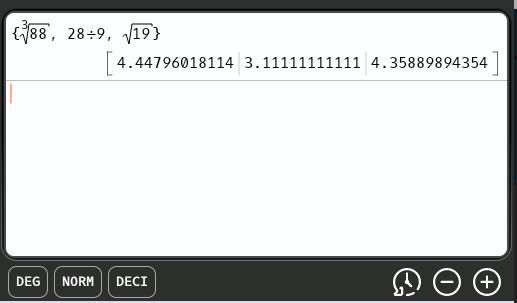
\(\dfrac{28}{9}.\ \sqrt{19},\ \sqrt[3]{88}\)
__
Additional comment
We know that √19 > √16 = 4, and ∛88 > ∛64 = 4, so the fraction 28/9 will be the smallest. That leaves us to compare √19 and ∛88, both of which are near the same value between 4 and 5.
One way to do the comparison is to convert these to values that need to have the same root:
√19 = 19^(1/2) = 19^(3/6) = sixthroot(19³)
∛88 = 88^(1/3) = 88^(2/6) = sixthroot(88²)
The roots will have the same ordering as 19³ and 88².
Of course, these values can be found easily using a calculator, as can the original roots. By hand, we might compute them as ...
19³ = (20 -1)³ = 20³ -3(20²) +3(20) -1 = 8000 -1200 +60 -1 = 6859
88² = (90 -2)² = 90² -2(2)(90) +2² = 8100 -360 +4 = 7744
Then the ordering is ...
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Answer:
the ordering is
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Step-by-step explanation:
If Carol pays $62.90 to fill the 17-gallon gas tank in her vehicle and she can drive 330
miles on one tank of gas, about how much does she pay per mile to drive her vehicle?
Answers
Answer:
Step-by-step explanation:10
The wholesale price for a chair is $165. A certain fumiture store marks up the wholesale price by 14%. Find the price of the chair in the furniture store. Round your answer to the nearest cent, as necessary.
Answers
Let g(x) be the indicated transformation of f(x) = −|3x| − 4. Stretch the graph of f(x) = −|3x| − 4 vertically by a factor of 3 and reflect it across the x-axis. Identify the rule and graph of g(x).
Answers
The final rule for g(x) is g(x) = 3|3x| + 12.
To stretch the graph of f(x) = −|3x| − 4 vertically by a factor of 3, we multiply the function by 3. This will result in a vertical stretching of the graph.
So, the rule for g(x) is g(x) = 3f(x).
Now, let's find the expression for g(x) using the given function f(x) = −|3x| − 4:
g(x) = 3f(x)
g(x) = 3(-|3x| - 4)
g(x) = -3|3x| - 12
This is the expression for g(x), which represents the transformed graph.
To reflect the graph of g(x) across the x-axis, we change the sign of the function. This means that the negative sign in front of the absolute value will become positive, and the positive sign in front of the constant term will become negative.
Therefore, the final rule for g(x) is g(x) = 3|3x| + 12.
Now, let's consider the graph of g(x). The graph will have the same shape as f(x), but it will be stretched vertically by a factor of 3 and reflected across the x-axis.
The original graph of f(x) = −|3x| − 4 is a V-shaped graph that opens downward and passes through the point (0, -4). The transformed graph of g(x) will have a steeper V-shape, opening downward, and passing through the point (0, 12) instead of (0, -4).
For more such questions on final rule visit:
https://brainly.com/question/30396691
#SPJ8
explain why the statement x < 3 or > 5 cannot be written 5 < x < 3
Answers
Answer:
This formula has no values, it is a false inequality. X can not be greater than 5, and less than 3.
Step-by-step explanation:
x < 3 or x > 5
This means, x is less than 3, but greater than 5.
Technically, you would write this as 5 < x < 3, however, this is a false inequality, and does not work.
any local College 63 of the male students are smokers in 147 or non-smokers the female students 70 or smokers and 130 are non-smokers a male student and a female student from the college are randomly selected for a survey what is the probability that both are smokers
Answers
Answer:
To find the probability that both a randomly selected male student and a randomly selected female student are smokers, we can use the formula for conditional probability: P(A and B) = P(A) * P(B|A), where A is the event that the male student is a smoker and B is the event that the female student is a smoker.
First, we need to find the probability that a randomly selected male student is a smoker:
P(A) = (number of male smokers) / (total number of male students) = 63 / (63 + 147) = 63/210
Next, we need to find the probability that a randomly selected female student is a smoker, given that the male student is a smoker:
P(B|A) = (number of female smokers and male smokers) / (number of male smokers) = 70 / 63
Finally, we can find the probability that both students are smokers by multiplying these two probabilities together:
P(A and B) = P(A) * P(B|A) = (63/210) * (70/63) = 0.09
So the probability that both a randomly selected male student and a randomly selected female student are smokers is 0.09 or 9%.
Step-by-step explanation:
PLEASE HELP ME
The function f(x) = -2(4)^x+1 +140
represents the number of tokens a child has x hours after arriving at an arcade.
What is the practical domain and range of the function?
If necessary, round to the nearest hundredth.
The practical domain of the situation is ?
The practical range of the situation is ?
PLEASE SEE PHOTO FOR FUNCTION

Answers
The function f(x) = -2(4)ˣ⁺¹ +140 represents the number of tokens a child has x hours after arriving at an arcade. The practical domain and range of the function are x ≥ 0 and The practical range of the situation is [140, ∞).
The given function is f(x) = -2(4)ˣ⁺¹+ 140, which represents the number of tokens a child has x hours after arriving at an arcade.
To determine the practical domain and range of the function, we need to consider the constraints and limitations of the situation.
For the practical domain, we need to identify the valid values for x, which in this case represents the number of hours the child has been at the arcade. Since time cannot be negative in this context, the practical domain is x ≥ 0, meaning x is a non-negative number or zero.
Therefore, the practical domain of the situation is x ≥ 0.
For the practical range, we need to determine the possible values for the number of tokens the child can have. Looking at the given function, we can see that the term -2(4)ˣ⁺¹represents a decreasing exponential function as x increases. The constant term +140 is added to shift the graph upward.
Since the exponential term decreases as x increases, the function will have a maximum value at x = 0 and approach negative infinity as x approaches infinity. However, due to the presence of the +140 term, the actual range will be shifted upward by 140 units.
Therefore, the practical range of the situation will be all real numbers greater than or equal to 140. In interval notation, we can express it as [140, ∞).
To summarize:
- The practical domain of the situation is x ≥ 0.
- The practical range of the situation is [140, ∞).
Know more about the domain here:
https://brainly.com/question/30096754
#SPJ8
a study of long-distance phone calls made from general electric reveled the length of the calls, in minutes, follows the normal probability distribution. the mean length of time per call was 4.5 minutes and the standard deviation was 0.70 minutes. what is the probability that calls last between 4.0 and 6.0 minutes?
Answers
The probability that calls last between 4.0 and 4.6 minutes will be around 0.4332.
we have to standardize the values and utilize the standard typical dispersion table or calculator.
To discover the z-scores for 4.0 and 6.0 minutes:
z1 = (4.0 - 6.0 ) / 0.70 = 2.8
z2 = (4.5 - 6.0 ) / 0.70= 2.1
Since Employing a standard ordinary conveyance table, we are able to discover the likelihood of the calls enduring between 4.0 and 4.6 minutes:
P(0 ≤ Z ≤ 2.1) = 0.4332
However the likelihood that calls final between 4.0 and 4.6 minutes is 0.4332, or around 0.4332.
To know more about probability refer to this :
brainly.com/question/24756209
#SPJ1
Solve for TV and SV. Select BOTH correct answers.
tv=8
sv=8√2
tv=8√2
sv-8

Answers
Answer:
TV = 8 , SV = 8\(\sqrt{2}\)
Step-by-step explanation:
given ST = TV , then
TV = 8
using Pythagoras' identity in the right triangle
SV² = ST² + TV² = 8² + 8² = 64 + 64 = 128 ( take square root of both sides )
SV = \(\sqrt{128}\) = \(\sqrt{64(2)}\) = \(\sqrt{64}\) × \(\sqrt{2}\) = 8\(\sqrt{2}\)
Simplify the expression 2³ × 2² A. 4⁵ B. 2⁶ C. 4⁶ D. 2⁵
Answers
Answer:
2^5
Step-by-step explanation:
The base is the same
2^3 * 2^2
We are multiplying, so we can add the exponents
2^3 * 2^2 = 2^(3+2) = 2^5
Answer: \(2^{5}\)
Explanation: I have written this problem on the whiteboard.
For the problem on the board, since our two powers have like bases of 2, we can multiply them together by simply adding their exponents.
So 2³ · 2² is just \(2^{5}\).
A common mistake in this problem would
be for students to say that 2³ · 2² is \(4^{5}\).
It's important to understand however that when applying your
exponent rules, your base in this case 2 will not change.

PLEASE SHOW YOUR WORK ON HOW TO SOLVE THIS PROBLEM!! BEST ANSWER ILL GET MARKED BRAINIEST!
4x+5/x+7
Answers
Answer:
x = 2.4
Step-by-step explanation:
4x + 5 / x + 7
combine like terms
X + 4x = 5x
5 + 7= 12
12/ 5x
Divide
12 /5= 2.4
X= 2.4
JKLM is a rhombus.
m/JMN = (-x+69)*
mZLMJ = (-6x +166)
K
N
M
Find the mZLKN.
label optional

Answers
The angle LKN in the rhombus is 62 degrees.
How to find angles in a rhombus?A rhombus is a quadrilateral that has 4 sides equal to each other. The sum of angles in a rhombus is 360 degrees.
Opposite angles are equal in a rhombus. The diagonals bisect each other at 90 degrees. Adjacent angles add up to 180 degrees.
Therefore, let's find ∠LKN as follows:
m∠JMN = (-x + 69)
m∠LMJ = (-6x + 166)
Therefore,
1 / 2 (-6x + 166) = -x + 69
-3x + 83 = -x + 69
-3x + x = 69 - 83
-2x = -14
x = -14 / -2
x = 7
Therefore,
∠LKN = 1 / 2 (-6x + 166)
∠LKN = 1 / 2 (-6(7) + 166)
∠LKN = 1 / 2 (-42 + 166)
∠LKN = 62 degrees
learn more on rhombus here: https://brainly.com/question/30995617
#SPJ1
Question 2 The current report quantitatively analyzes three variables - load factors, revenue passenger mile, and available seat miles for American Airlines. The data retrieved for the analysis was extracted from the Bureau of Transportation Statistics, focusing on domestic flights from January 2006 to December 2012. The quantitative analysis focused on finding critical statistical values like mean, median, mode, standard deviation, variance, and minimum/maximum variables. Table 2: Summary Statistics of American Airlines (Domestic) Revenue Passenger Miles Mean 6,624,897 Median 6,522,230 Mode NONE Minimum 5,208,159 Maximum 8,277,155 Standard Dev 720,158.571 Variance 518,628,367,282.42 Load Factors Mean 82.934 Median 83.355 Mode 84.56 Minimum 74.91 Maximum 89.94 Standard Dev 3.972 Variance 15.762 Revenue Passenger Miles 9000000 8000000 7000000 6000000 5000000 4000000 3000000 2000000 1000000 0 0 10 American Airlines (Domestic) Performance 20 30 ● Revenue Passenger Miles 40 50 Load Factors Available Seat Miles 60 Mean 7,984,735 Median 7,753,372 Mode NONE Minimum 6,734,620 Maximum 9,424,489 Standard Dev 744,469.8849 Variance 554,235,409,510.06 70 80 Linear (Revenue Passenger Miles) 90 100 Figure 1: American Airlines (Domestic) Performance Write a report based on the given data. Please include additional tests such as hypothesis testing, skewness, z statistic, level of significance, and other necessary tests, as well as a discussion of the results obtained.
Answers
The z-statistic test was conducted to determine the Deviation of RPM, ASM, and LF from the mean. The test indicates that RPM, ASM, and LF significantly deviate from the mean.
Report on the Analysis of American Airlines (Domestic) PerformanceThe quantitative analysis focused on three variables- load factors, revenue passenger miles, and available seat miles for American Airlines.
The Bureau of Transportation Statistics data for domestic flights from January 2006 to December 2012 was retrieved for the analysis. The quantitative analysis also focused on finding critical statistical values like mean, median, mode, standard deviation, variance, and minimum/maximum variables. The results of the data are summarized in Table 2. Revenue Passenger Miles (RPM) mean is 6,624,897, the median is 6,522,230, and mode is NONE. The minimum is 5,208,159 and the maximum is 8,277,155. The standard deviation is 720,158.571, and the variance is 518,628,367,282.42.
Load Factors (LF) mean is 82.934, the median is 83.355, and mode is 84.56. The minimum is 74.91, and the maximum is 89.94. The standard deviation is 3.972, and the variance is 15.762. The Available Seat Miles (ASM) mean is 7,984,735, the median is 7,753,372, and mode is NONE. The minimum is 6,734,620, and the maximum is 9,424,489. The standard deviation is 744,469.8849, and the variance is 554,235,409,510.06.Figure 1 above displays the performance of American Airlines (Domestic).
The mean RPM is 7,984,735, and the linear regression line is y = 50584x - 2.53E+8. The linear regression line indicates a positive relationship between RPM and year, with a coefficient of determination, R² = 0.6806. A coefficient of determination indicates the proportion of the variance in the dependent variable that is predictable from the independent variable. Therefore, 68.06% of the variance in RPM is predictable from the year. A one-way ANOVA analysis of variance test was conducted to determine the equality of means of three groups of variables; RPM, ASM, and LF. The null hypothesis is that the means of RPM, ASM, and LF are equal.
The alternative hypothesis is that the means of RPM, ASM, and LF are not equal. The level of significance is 0.05. The ANOVA results indicate that there is a significant difference in means of RPM, ASM, and LF (F = 17335.276, p < 0.05). Furthermore, a post-hoc Tukey's test was conducted to determine which variable means differ significantly. The test indicates that RPM, ASM, and LF means differ significantly.
The skewness test was conducted to determine the symmetry of the distribution of RPM, ASM, and LF. The test indicates that the distribution of RPM, ASM, and LF is not symmetrical (Skewness > 0).
Additionally, the z-statistic test was conducted to determine the deviation of RPM, ASM, and LF from the mean. The test indicates that RPM, ASM, and LF significantly deviate from the mean.
For more questions on Deviation .
https://brainly.com/question/24298037
#SPJ8
a can complete a piece of work in 10 days B can do it in 12 days C can do it in 15 days in how many days will they finish the work if they work together
Answers
hope it helps you

If 9% of a number is 75, find 3% of that number.
Delta math again.
Answers
Answer:
25
Step-by-step explanation:
\(0.09a=75\\a=\frac{75}{0.09} \\0.03*a=0.03*\frac{75}{0.09} =25\)
Find the value of X from the photo

Answers

Wyatt was out at a restaurant for dinner when the bill came. He wanted to leave a tip of 19%. What number should he multiply the cost of the meal by to find the total plus tip in one step?
Answers
Answer:
The cost of the meal should be multiplied by 1.19.---------------------------------------
Let the cost of the meal be x.
Adding a tip of 19%:
x + 19% = x + 0.19x = x (1 + 0.19) = 1.19xAnswer:
Wyatt should multiply with 1.19.
Step-by-step explanation:
Forming the expression,
→ 1 + (19% of 1)
Now the required number is,
→ 1 + (19% of 1)
→ 1 + ((19/100) × 1)
→ 1 + (19/100)
→ 1 + 0.19 = 1.19
Hence, required number is 1.19.
How many pounds of butterfat are in one gallon of whole milk that weighs approximately 8.6 lb. And contains about 4% butterfat
Answers
Answer:
Below
Step-by-step explanation:
8.6 lb x 4 % fat = 8.6 x .04 = .344 lb fat
_____
which two integers is between /-83
Answers
The two integers that are between -83 and +83 are -82 and +82.
What is integers ?
In mathematics, integers are a set of whole numbers that include positive numbers, negative numbers, and zero. Integers do not include fractional or decimal parts, they are the numbers in the set {..., -3, -2, -1, 0, 1, 2, 3, ...}. Integers are commonly used in many areas of mathematics, including arithmetic, algebra, and number theory.
There are multiple pairs of integers that are between -83 and 83.
Here are two examples:
-50 and 50: These are integers that are between -83 and 83. Any integer between -83 and -50, or between 50 and 83, is also between -83 and 83. We can represent this range on a number line as follows:
-83 -50 0 50 83
|----------------|----------------|----------------|----------------|
The integers between -83 and 83 are represented by the shaded portion of the number line.
-75 and 75: These are also integers that are between -83 and 83. Any integer between -83 and -75, or between 75 and 83, is also between -83 and 83. We can represent this range on a number line as follows:
-83 -75 0 75 83
|----------------|----------------|----------------|----------------|
The integers between -83 and 83 are represented by the shaded portion of the number line.
In general, any pair of integers that are equidistant from 0 and within a range of 83 from 0 will be between -83 and 83.
Learn more about Integers click here:
https://brainly.com/question/17695139
#SPJ1
Solve the system by using any method. If a system does not have one unique solution, state whether the system is inconsistent or whether the equations are
dependent.
2x+y=6
x+1/2y=3
Answers
The simultaneous equations 2x + y = 6 and x + y/2 = 3 are dependent because both equations are the same and they have an infinite number of solutions that satisfy both equations.
What are dependent simultaneous equations?A system of simultaneous equations is called dependent if it has infinitely many solutions. In other words, one equation in the system can be obtained by adding or subtracting multiples of the other equation(s), or if all the equations represent the same line or plane in higher dimension.
We can write the equations as:
2x + y = 6...(1)
x + y/2 = 3...(2)
equation (2) can be rewritten as follows:
(2x + y)/2 = 3 {simplifying the left hand side to a single denominator}
2x + y = 2 × 3 {cross multiplication}
2x + y = 6
We can observe that equations (1) and (2) are the same. Any value of x and y that satisfies the equation 2x + y = 6 will also satisfy the second equation, x + y/2 = 3.
In conclusion, the simultaneous equations 2x + y = 6 and x + y/2 = 3 are dependent because both equations are the same, hence they have an infinite number of solutions that satisfy both equations.
Know more about equation here:https://brainly.com/question/26523945
#SPJ1
Lucy is riding on a bike course that is 25 miles long. So far, she has ridden 24 miles of the course. What percentage of the course has Lucy ridden so far
Answers
Answer:
96%
Step-by-step explanation:
The fraction is converted to a percentage by multiplying it by 100%.
Lucy has ridden 24 of 25 miles.
(24/25) × 100% = 96%
She has ridden 96% of the course so far.
To make a big batch of cookies for her father, Annmarie needs 1 1/4 pounds of chocolate chips, 3/4 pounds of walnuts, and 12 ounces of raisins. How many ounces of these three ingredients does she need in all?
A. 28ounces
B. 44ounces
C. 48ounces
D. 76ounces
Answers
Answer: B. 44 ounces
Answer:
what was it ??
Step-by-step explanation: i taking the test
test test test test test test test test test test
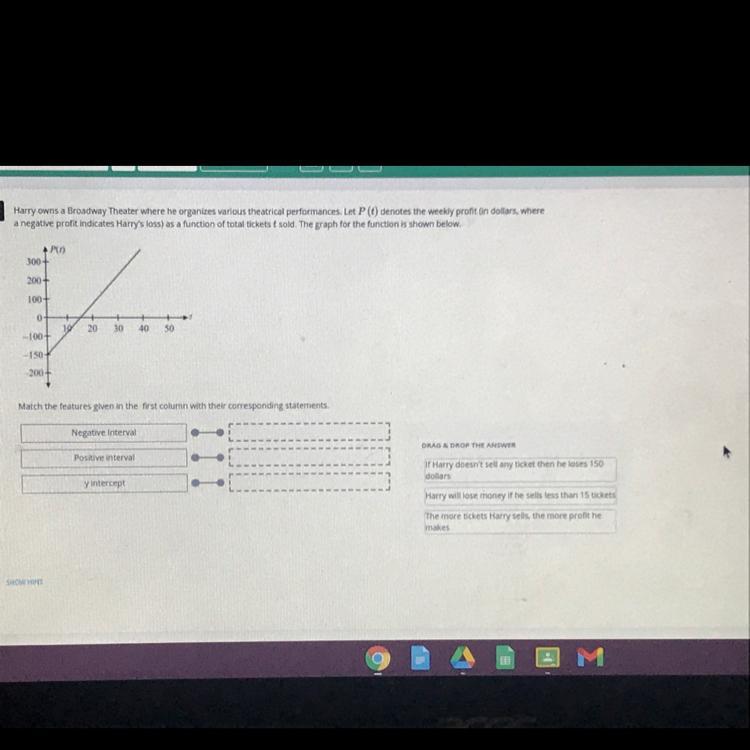
Match the features given in the first column with their corresponding statements
Answers
given the line that represents P(t) which represent the profit of Harry
We will match the features given in the first column with their corresponding statements
Negative interval:
Harry will lose money if he sells less than 15 tickets
Positive interval:
The more tickets Harry sell, the more profit he makes
The triangular faces of the prism shown are equilateral triangles with perimeter 30 cm. Use a net to find the surface area of the prism.

Answers
Explanation:
\(\begin{gathered} The\text{ surface area is made up of the two equilateral triangles shown above as well as the three rectangles.} \\ Area\text{ of Triangles = 2\lparen}\frac{1}{2}b*h) \\ If\text{ the perimeter of the triangle is 30cm, the length of one side = 30/3 = 10 = base} \\ Area\text{ = 2\lparen}\frac{1}{2}*10*8.7) \\ \text{ =87} \\ Area\text{ of the three rectangles = 3\lparen length*width\rparen } \\ \text{ =3\lparen10*12\rparen} \\ \text{ =360} \\ Total\text{ Surface Area = 360 + 87 = 447} \end{gathered}\)Surface Area of the two triangles in the net = 2*(0.5*b*h)
= 2*(0.5*10*8.7)
=87
Surface Area of three rectangles in the net = 3(l*b)
= 3*12*10
=360
Answer: Total Surface area = 360 + 87 = 447

Please someone help me

Answers
Answer:
C) <BAC ≈ <QPR and BC ≈ QR
Step-by-step explanation:
C) <BAC ≈ <QPR and BC ≈ QR
How do u convert kilometres into minutes
Example 0.8kilometer what till ut b in minutes woukd u times by 70
Answers
Answer:
It is not possible
Step-by-step explanation:
Given
0.8km
Required
Convert to minutes
In conversion, only units of the same metric can be converted.
i.e.
You can convert meters to miles (they both measure distance)
You can convert seconds to hours (they both measure time)
You can convert kilogram to pounds (they both measure weight)
But in the given question, you attempt to convert from distance to time.
This is not possible, because time and distance are different measurements
The marketing manager for an automobile manufacturer is interested in determining the proportion of new compact-car owners who would have purchased a GPS navigation system if it had been available for an additional cost of $300. The manager believes from previous information that the proportion is 0.30. Suppose that a survey of 200 new compact-car owners is selected and 79 indicate that they would have purchased the GPS navigation system. If you were to conduct a test to determine whether there is evidence that the proportion is different from 0.30, which test would you use
Answers
Answer:
Two-tailed test.
Step-by-step explanation:
There are two types of tests:
One-tailed tests and two-tailed tests.
When we only test if the mean is less or more than a value, we have a one-tailed test.
When we test if the mean is different from a value, we have a two-tailed test.
If you were to conduct a test to determine whether there is evidence that the proportion is different from 0.30, which test would you use?
Test if it is different, so a two-tailed test.
(Diversifying Portfolios MC)
Two investment portfolios are shown with the amount of money placed in each investment and the ROR.
Investment
Tech Company Stock $2,800
Government Bond $3,200
Junk Bond
$950
Common Stock
$1,500
Portfolio 1 Portfolio 2
$1,275
$2,200
$865
$1,700
O Portfolio 2 earns $38.17 more.
Which portfolio earns the most, and by how much?
O Portfolio 1 earns $38.17 more.
O Portfolio 1 earns $76.20 more.
ROR
-3.75%
2.95%
4.56%
O Portfolio 2 earns $76.20 more..
7.18%
Answers
Answer: Portfolio 1:
Tech Company Stock: $2,800 * 2.95% = $82.60
Government Bond: $3,200 * 4.56% = $145.92
Total return for Portfolio 1 = $82.60 + $145.92 = $228.52
Portfolio 2:
Junk Bond: $950 * (-3.75%) = -$35.63
Common Stock: $1,500 * 7.18% = $107.70
Total return for Portfolio 2 = -$35.63 + $107.70 = $72.07
From the calculations, we can see that Portfolio 1 earns $228.52 in returns, while Portfolio 2 earns $72.07. Therefore, Portfolio 1 earns $228.52 - $72.07 = $156.45 more than Portfolio 2.
Step-by-step explanation:
22. a) Out of 30 students in a class, two-third were successful to get A grade in Maths test. Among these successful students, one-quarter got A grade even in science also. (i) What fraction of the successful students got A+ grade in science? (ii) How many students were successful to get A+ grade in science? (iii) How many students got other than A+ grade in these two subjects?
Answers
Answer:
i) 1/6
ii) 5 students
iii) maths 10
science 25
Step-by-step explanation:
total=30
A grade in mathts =2/3x30.
=20 students
i) 1/4of successful got A in science
= 1/4x20 = 5 students
fraction = 5/30
=1/6
those who got other grades
maths 30-20= 10
science 30-5=25
Use properties of operations to generate an expression that is equivalent to the given expression. −4(2x−5)+12−3x
Answers
Using properties of operations the equivalence of the expression
−4(2x − 5) + 12 − 3x is generated to be -11x + 32
How to generate the equivalence of the expressionThe math question is solved using the idea of PEMDAS which is an acronym for order of arrangement of mathematical operations as
the full meaning include
P - parenthesis
E - exponents
M - multiplication
D - division
A - addition
S - subtraction
Parenthesis
= −4(2x − 5) + 12 − 3x
= -8x + 20 + 12 - 3x
collecting like terms and addition
= -8x + 20 + 12 - 3x
= -8x - 3x + 20 + 12
= -11x + 32
the equivalence expression is -11x + 32
Learn more about PEMDAS here:
https://brainly.com/question/29393553
#SPJ1