A research study investigated differences between male and female students. Based on the study results, we can assume the population mean and standard deviation for the GPA of male students are µ = 3. 5 and Ď = 0. 5. Suppose a random sample of 100 male students is selected and the GPA for each student is calculated. Find the interval that contains 95. 44 percent of the sample means for male students.
Answers
Using the normal distribution and the central limit theorem, it is found that the interval that contains 99.44% of the sample means for male students is (3.4, 3.6).
In a normal distribution with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
It measures how many standard deviations the measure is from the mean. After finding the z-score, we look at the z-score table and find the p-value associated with this z-score, which is the percentile of X. By the Central Limit Theorem, the sampling distribution of sample means of size n has standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).In this problem:
The mean is of \(\mu = 3.5\).The standard deviation is of \(\sigma = 0.5\).Sample of 100, hence \(n = 100, s = \frac{0.5}{\sqrt{100}} = 0.05\)The interval that contains 95.44% of the sample means for male students is between Z = -2 and Z = 2, as the subtraction of their p-values is 0.9544, hence:
Z = -2:
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(-2 = \frac{X - 3.5}{0.05}\)
\(X - 3.5 = -0.1\)
\(X = 3.4\)
Z = 2:
\(Z = \frac{X - \mu}{s}\)
\(2 = \frac{X - 3.5}{0.05}\)
\(X - 3.5 = 0.1\)
\(X = 3.6\)
The interval that contains 99.44% of the sample means for male students is (3.4, 3.6).
You can learn more about the normal distribution and the central limit theorem at https://brainly.com/question/24663213
Related Questions
What is the value of 4 in the following numbers( a)43. ( b)4631
Answers
The value of 4 in this number is 4 units or 4 ones and the value of 4 in this number is 4 hundreds or 400.
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words.
A number is an arithmetic value used for representing the quantity and used in making calculations. A written symbol like “3” which represents a number is known as numerals. A number system is a writing system for denoting numbers using digits or symbols in a logical manner.
The value of 4 in the following numbers is as follows:a) 43 - The value of 4 in this number is 4 units or 4 ones.b) 4631 - The value of 4 in this number is 4 hundreds or 400.
To know more about numbers:
https://brainly.com/question/24908711
#SPJ11
4.The profit on a watch is 25% of the cost price. If the profit is $200, find:
a. The cost price of the watch
b. The selling price of the watch
Answers
Answer:
A.) $800
B.) $1,000
help me please
i need help lol

Answers
Answer:
<3 and <4 are supplementary
Step-by-step explanation:
<3 and <4 form a linear pair, so they are supplementary (=180 degrees)
In a group of 25 boys , 8 are in the Science League team and 13 in the math League team and 6 in both the teams. How many are not in any team?
Answers
first subtract 6 from 8 to get 2 (since it's easier) because those 6 girls are on the math league team as well
next add 2 and 13 to get 15
last subtract 15 from 25 to get 10
What is the equation that can be used to find a percent of a number?
Answers
Answer:
Percent · Base = Amount.
Step-by-step explanation:
Use n for the unknown (percent).
Divide to undo the multiplication of n times 72.
Move the decimal point two places to the right to write the decimal as a percent.
Hope this helps!(:
Answer:
part = percent • whole
Step-by-step explanation:
an interesting question is: which questions/problems have algorithms that can be applied to compute solutions? we know there are questions with ""yes or no"" answers for which there is no algorithm.
Answers
There are many questions and problems for which efficient algorithms exist, but there are also many others for which no efficient algorithm is currently known, and some for which it has been proven that no algorithm can exist.
The field of computer science and mathematics known as computational complexity theory studies which problems can be solved by algorithms and how efficient those algorithms are. The theory classifies problems into different complexity classes based on the resources required to solve them, such as time, space, or the number of processors.
There are certain classes of problems for which efficient algorithms are known to exist. For example, sorting a list of numbers or searching for an item in a database can be done in polynomial time, which means that the time required to solve the problem grows at most as a polynomial function of the size of the input.
On the other hand, there are problems for which no efficient algorithm is currently known. One famous example is the traveling salesman problem, which asks for the shortest possible route that visits a set of cities and returns to the starting point. While algorithms exist to solve this problem, they have an exponential running time, meaning that the time required to solve the problem grows exponentially with the size of the input, making them infeasible for large inputs.
There are also problems for which it has been proven that no algorithm can exist that solves them efficiently. For example, the halting problem asks whether a given program will eventually stop or run forever. It has been proven that there is no algorithm that can solve this problem for all possible programs.
In summary, there are many questions and problems for which efficient algorithms exist, but there are also many others for which no efficient algorithm is currently known, and some for which it has been proven that no algorithm can exist.
To know more about computational complexity refer to
https://brainly.com/question/30546818
#SPJ11
A backpack that normally sells for $39 is on sale for $25. Find the
percent of change.
Answers
Answer: To find the discount, simply multiply the original selling price by the %discount:
ie: 39 x 33/100= $12.87
So, the discount is $12.87.
Step-by-step explanation: To find the sale price, simply minus the discount from the original selling price:
ie: 39- 12. 87= 26.13
So, the sale price is $26.13
Use the Remainder Theorem to determine whether or not x + 3 is a divisor of p (x) = 2x^3 + 4x^2 - 2x + 12
PLEASE SHOW WORK.

Answers
Step-by-step explanation:
This is answer. I'm sri lankan. But our a/l exam have this mathematics questions

The remainder when the polynomial p(x) = 2x³ + 4x² - 2x + 12 is divided by x + 3 is -6.
A polynomial is an expression consisting of the operations of addition, subtraction, multiplication of variables.
The remainder theorem states that for a polynomial, f(x) divided by a linear polynomial , x - a, the remainder is equal to f(a).
Given the polynomial; p(x) = 2x³ + 4x² - 2x + 12, since it is divided by x + 3, hence:
x + 3 = 0
x = -3
p(-3) = 2(-3)³ + 4(-3)² - 2(-3) + 12 = -6
Hence the remainder when the polynomial p(x) = 2x³ + 4x² - 2x + 12 is divided by x + 3 is -6.
Find out more at: https://brainly.com/question/13416073
6. Write the parametric equations of the line through the point P (-6, 4, 3), that is perpendicular to both the lines with equations: [3 marks]
L1: (x, y, z) = (0, -10, -2) + s(4,6,-3)
L2: (x, y, z)=(5, 5, -5) + t(3, 2, 4)
Answers
The parametric equations of the line through the point P (-6, 4, 3), that is perpendicular to both the lines with equations L1: (x, y, z) = (0, -10, -2) + s(4,6,-3) and L2: (x, y, z)=(5, 5, -5) + t(3, 2, 4) is given by: x= -6 + 18t,y= 4 - 39t, and z= 3 - 10t.
Let us first find the direction vector of the lines L1 and L2.
From line L1, the direction vector is given by:
d1= 4i + 6j - 3k
From line L2, the direction vector is given by:
d2= 3i + 2j + 4k
Now, let us find the vector that is perpendicular to both d1 and d2 by taking their cross product:
n= d1×d2= (4i + 6j - 3k)×(3i + 2j + 4k)
Simplifying this gives:
n= 18i - 39j - 10k
This is the normal vector of the plane that contains both lines L1 and L2.
Now, we want to find a line that passes through the point P(-6, 4, 3) and is perpendicular to this plane.
A line that is perpendicular to this plane is parallel to the normal vector.
So we can use this normal vector as the direction vector of the line we want to find.
The parametric equations of the line are:
x= -6 + 18t,y= 4 - 39t,z= 3 - 10t,where t is a parameter.
Thus, the answer is that the parametric equations of the line through the point P (-6, 4, 3), that is perpendicular to both the lines with equations:
L1: (x, y, z) = (0, -10, -2) + s(4,6,-3) and
L2: (x, y, z)=(5, 5, -5) + t(3, 2, 4) is given by:
x= -6 + 18t,y= 4 - 39t, and z= 3 - 10t.
To know more about parametric equations visit:
https://brainly.com/question/29275326
#SPJ11
The equation of the hyperbola that has a center at ( 6 , 9 ) , a focus at ( 11 , 9 ) , and a vertex at ( 9 , 9 ) (x−C)^2/A^2−(y−D)^2/B^2=1
Answers
Answer:
\(A=-3\)
\(C=6\)
\(B=4\)
\(D=9\)
Step-by-step explanation:
From the question we are told that:
Center of hyperbola at ( 6 , 9 )
Focus of hyperbola at ( 11 , 9 )
Vertex of hyperbola at ( 9 , 9)
Equation of hyperbola \(\frac{(x-C)^2}{A^2} -\frac{(y-D)^2}{B^2}=1\)
Generally the C and D of the hyperbola equation is mathematically given by
\(Centers (6,9)\)
\(C=6\)
\(D=9\)
Generally the A and B a of the hyperbola equation is mathematically given by
\(A=x_c-x_v\)
\(A=6-9\)
\(A=-3\)
\(C'=x_c-x_f\)
\(C'=6-11\)
\(C'=-5\)
Therefore with Center,Focus ,Vertex on the same line
\(B^2=C'^2-A^2\)
\(B^2=(-5^2)-(-3^2)^2\)
\(B^2=(25)-(9)\)
\(B^2=16\)
\(B=4\)
write the equation of a line given its slope m=6 and its y intercept b= -5 . What would the answer be ?
Answers
Answer:
y= 6x-5
Step-by-step explanation:
So you can plug it into the equation
y= mx + b
y= 6x-5
hope that helps
Q3 Estimate the monthly average daily radiation on a horizontal surface \( \mathrm{H} \) in June in Amman given the following : Monthly average hours per day of sunshine in June 10 hours Climate type:
Answers
The estimated monthly average daily radiation on a horizontal surface in June in Amman is approximately 7.35 kWh/m(^2)/day.
To estimate the monthly average daily radiation on a horizontal surface H in June in Amman, we can use the following equation:
\([H = S \times H_s \times \frac{\sin(\phi)\sin(\delta)+\cos(\phi)\cos(\delta)\cos(H_a)}{\pi}]\)
where:
S is the solar constant, which is approximately equal to 1367 W/m(^2);
\(H(_s)\) is the average number of sunshine hours per day in Amman in June, which is given as 10 hours;
(\(\phi\)) is the latitude of the location, which for Amman is approximately 31.9 degrees North;
(\(\delta\)) is the solar declination angle, which is a function of the day of the year and can be calculated using various methods such as the one given in the answer to Q1;
\(H(_a)\) is the hour angle, which is the difference between the local solar time and solar noon, and can also be calculated using various methods such as the one given in the answer to Q1.
Substituting the given values, we get:
\([H = 1367 \times 10 \times \frac{\sin(31.9)\sin(\delta)+\cos(31.9)\cos(\delta)\cos(H_a)}{\pi}]\)
Since we are only interested in the monthly average daily radiation, we can assume an average value for the solar declination angle and the hour angle over the month of June. For simplicity, we can assume that the solar declination angle (\(\delta\)) is constant at the value it has on June 21, which is approximately 23.5 degrees North. We can also assume that the hour angle \(H(_a)\) varies linearly from -15 degrees at sunrise to +15 degrees at sunset, with an average value of 0 degrees over the day.
Substituting these values, we get:
\([H = 1367 \times 10 \times \frac{\sin(31.9)\sin(23.5)+\cos(31.9)\cos(23.5)\cos(0)}{\pi}]\)
Simplifying the equation, we get:
\([H \approx 7.35 \text{ kWh/m}^2\text{/day}]\)
Therefore, the estimated monthly average daily radiation on a horizontal surface in June in Amman is approximately 7.35 kWh/m(^2)/day.
Learn more about "average daily radiation " : https://brainly.com/question/32911494
#SPJ11
A cinema screens two different short films at two separate rooms at regular intervals throughout the day. The first film lasts for $$50 minutes, while the second film lasts for $$30 minutes. There are $$10-minute breaks between the screening of a film in each room. If the cinema starts screening both films at $$2:45 pm when it opens for the day, what is the next time that both films will start screening at the same time?
Answers
Answer:
4: 45pm
Step-by-step explanation:
First Film = 50 minutes
Second Film = 30 minutes
Cinema start screening time = 2:45 pm
- Both Film start screening
At 3: 15 pm
- Second film ends
- First film is till screening ( 20 minutes left)
- Break Commences
3: 25
- First film is till screening ( 10 minutes left)
- Break Ends
- Second film starts screening
3 : 35 pm
- First film ends
- Break Commences
- Second film is till screening ( 20 minutes left)
3 : 45
- Second film is till screening ( 10 minutes left)
- Break Ends
- First film starts screening
3 : 55 pm
- Second film ends
- First film is till screening ( 40 minutes left)
- Break Commences
4 : 05 pm
- Break Ends
- First Film is till screening ( 30 minutes left)
- Second film starts screening
4: 35 pm
- Both Film ends
- Break Commences
4: 45pm
- Break Ends
- Both Films start screening
PLEASEEE HELP ILL GIVE BRAINLIEST btw there are 2 attachments so u could see all the answer choices

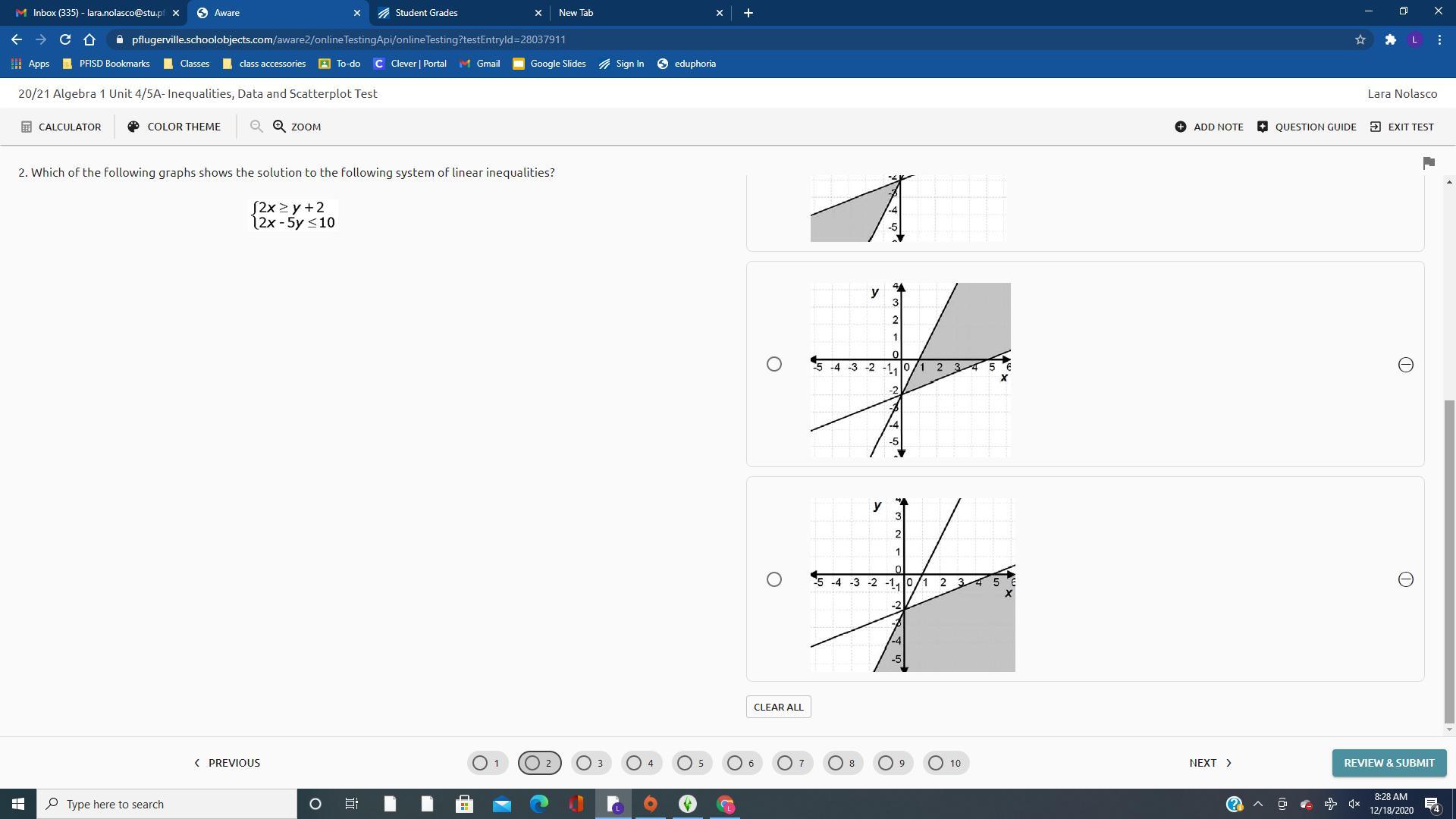
Answers
Answer:
1) C
Step-by-step explanation:
Step 1)
First we have to plot ↓
2x ≥ y + 2
And that looks like Image 1
Step 2)
Second we have to plot ↓
2x - 5y ≤ 10
and that looks like Image 2


This is lines , functions and systems. Graphing a line through a given point with a given slope.

Answers
The slope of the line is given as -2/3.
We are also given the point (1, 1) in which this line passes through.
Before we can plot the graph of the line, we need to know the equation of the line first.
The values given are more than enough to find the equation of the line.
The formula used to get the equation of the line is given below:
\(\begin{gathered} m=\frac{y-y_1}{x-x_1} \\ \text{where,} \\ m=\text{slope} \\ _{} \\ x_1,y_1=\text{ The given point} \end{gathered}\)Now, with this formula, let us find the equation of the line.
\(\begin{gathered} y_1=1,x_1=1,m=-\frac{2}{3} \\ m=\frac{y-y_1}{x-x_1} \\ \\ -\frac{2}{3}=\frac{y-1}{x-1}\text{ (Cross multiply)} \\ \\ -2\times(x-1)=3(y-1) \\ -2x+2=3y-3 \\ \text{add 3 to both sides} \\ -2x+2+3=3y-3+3 \\ 3y=-2x+5 \end{gathered}\)Thus, the equation of the line is:
\(3y=-2x+5\)Now, using a graph calculator, let us plot this equation.
After doing this, the following is the result:

five cards each are to be dealt to two players. if one player has the ace of spades, what is the probability that the other player has the ace of hearts?
Answers
The probability that the other player has the ace of hearts is 25/102.
There are a total of 52 cards in a standard deck, and since one player has the Ace of Spades, that leaves 51 cards remaining.
Of those remaining 51 cards, there is only one Ace of Hearts,
So, the probability of the other player having the Ace of Hearts is 1/51.
However, there are 4 suits in a deck of cards, and since we don't know the suit of the Ace of Spades, we must account for the possibility that the Ace of Hearts has already been dealt. If the Ace of Hearts has been dealt, then there are only 50 cards remaining, and the probability of the other player having the Ace of Hearts is 0.
So the overall probability is the probability that the Ace of Hearts hasn't been dealt, which is 50/51, multiplied by the probability that the Ace of Hearts is in the same suit as the Ace of Spades, which is 3/12.
(since there are 3 Aces remaining in the same suit as the Ace of Spades, out of 12 remaining cards of that suit)
So the overall probability is:
(50/51) * (3/12) = 25/102
To know more about the "probability": https://brainly.com/question/25688842
#SPJ11
Fatima is taking a test that is 45 minutes long.
She finishes the test at 10:50 a.m.
What time did she start the test?
Answers
Answer:10:05
Step-by-step explanation:
subtract 45 from 50!
Answer:
She started the test at 10:05 am
Step-by-step explanation:
Take the end time and subtract the time of the test
10:50-45 = 10:05
She started the test at 10:05 am
Please please help me with this question please
1. Define theoretical probability
2. What is the probability of each of the following?
a) picking the 9 of clubs from a deck of cards————- (fraction)
b) flipping heads with a coin ————-(decimal)
c) picking a diamond from a deck of cards
———-—-(percent)
d) rolling a 3 with 1 die ———(fraction)
e) rolling an even number with 1 die ———————(decimal)
f) flipping heads or tails with a coin —————(percent)
3. Define experimental probability.
Answers
Answer:
1. Theoretical probability is the probability or likelihood something will happen based on reasoning and expectations.
3. Experimental probability is the probability that something actually happened based on an experiment being done multiple times.
2.
a) 1/52
b) 0.5
c) 25%
d) 1/6
e) 50%
f) 100%
Step-by-step explanation:
2.
a) There are 52 cards in a deck of cards, and you are pulling one specific card. There is only one 9 of clubs in the deck of 52 cards. 1/52
b) There are only two options for flipping a coin, heads and tails. 1/2 = 0.5
c) 1/4 of the deck of cards are diamonds, and 1/4 = 25/100 = 25%
d) one die has 1, 2, 3, 4, 5, 6 as options. Rolling a 3 is a 1 out of 6 chance = 1/6
e) Again, our options are 1, 2, 3, 4, 5, 6. Of those, 2, 4, 6 are even. 3 out of 6 chance it is even. 3/6 = 1/2 = 0.5
f) There are only two options, heads or tails. Landing on either heads or tails is guaranteed...so 100%
Please let me know if you have questions.
do anybody know the answer to dis
53.9 - 5.07
Answers
Answer:
48.83
Step-by-step explanation
This is an example of an Undamped Forced Oscillation where the phenomenon of Pure Resonance Occurs. Find the solution of the initial value problem: x" + 9x = 12 sin(3t), x(0) = x'(0) = 0 x(t) = Graph the solution to confirm the phenomenon of Pure Resonance
Answers
The solution to the initial value problem is x(t) = 4/27 sin(3t).
We have solved the initial value problem x" + 9x = 12 sin(3t), x(0) = x'(0) = 0 and graphed the solution to confirm the phenomenon of pure resonance.
First, we need to solve the differential equation x" + 9x = 12 sin(3t) using standard techniques from differential equations. We can begin by assuming a solution of the form x(t) = A sin(3t) + B cos(3t), where A and B are constants to be determined. Taking the first and second derivatives of x(t), we find
=> x'(t) = 3A cos(3t) - 3B sin(3t) and x''(t) = -9A sin(3t) - 9B cos(3t).
Substituting these expressions into the differential equation, we obtain
=> -9A sin(3t) - 9B cos(3t) + 9A sin(3t) + 9B cos(3t) = 12 sin(3t).
Simplifying, we get 0 = 12 sin(3t), which implies that sin(3t) = 0.
This has solutions at t = 0, pi/3, 2pi/3, pi, etc.
These are the resonant frequencies of the system, where the external force is in phase with the natural frequency of the system.
To find the constants A and B, we can use the initial conditions x(0) = 0 and x'(0) = 0. Substituting t = 0 into the expressions for x(t) and x'(t), we get A = 0 and B = 0.
Therefore, the solution to the initial value problem is x(t) = 4/27 sin(3t).
Now let's graph the solution to confirm the phenomenon of pure resonance. We can use a graphing calculator or software to plot the function x(t) = 4/27 sin(3t) over a suitable range of t. We can also graph the external force 12 sin(3t) to see how it compares to the motion of the system.
To know more about graph here
https://brainly.com/question/17267403
#SPJ4

There are
windows for every 3penguins.
There are
windows for every 11 penguin.
Answers
in the first 18 and the second 6
x intercepts of -12x^2+108x=h and the y intercept
Answers
Answer:
x: 0 or 9
y-int: 0
Q5) A hot air balloon has a velocity of 50 feet per minute and is flying at a constant height of 500 feet. An observer on the ground is watching the balloon approach. How fast is the distance between the balloon and the observer changing when the balloon is 1000 feet from the observer?
Answers
When the balloon is 1000 feet away from the observer, the rate of change in that distance is roughly 1/103 feet per minute.
Let x be the horizontal distance between the balloon and the observer.
Using Pythagoras Theorem;
(x²) + (500²) = (1000²)
x² = (1000²) - (500²)
x² = 750000x = √750000x = 500√3
Then, the rate of change of x with respect to time (t) is;dx/dt = velocity of the balloon / (dx/dt)2 = 50 / 500√3= 1/10√3 ft/min.
Thus, the rate of change of the distance between the balloon and the observer when the balloon is 1000 feet from the observer is approximately 1/10√3 ft/min.
To know more about distance click on below link :
https://brainly.com/question/29146836#
#SPJ11
Susan won $2000 and invested it into an account with an annual interest rate of 3.2%. If her investment were compounded monthly, which expression best represents the value of her investment after t years
Answers
Answer:
FV= PV*(1+i)^t
Step-by-step explanation:
Giving the following information:
Initial investment (PV)= $2,000
Interest rate (i)= 3.2% = 0.032
Number of periods= t
To calculate the future value (FV) of the investment, we need to use the following formula:
FV= PV*(1+i)^t
For example, Susan invests for 4 years:
FV= 2,000*(1.032^4)
FV= $2,268.55
The expression best represents the value of her investment after t years is \(FV= PV\times (1+i)^t\)
Calculation of the expression:Since
Susan won $2000 and invested it into an account with an annual interest rate of 3.2%.
Here Number of periods= t
Therefore we can conclude that The expression best represents the value of her investment after t years is \(FV= PV\times (1+i)^t\)
Learn more about an account here:https://brainly.com/question/3096424
someone answer this correctly please, I’ll give you brainliest and your getting 50 points someone answer this no fraud answers don’t be weird.

Answers
The proof of the congruent sides RU and TS is given below.
What is congruent triangles?
In any orientation, two triangles are said to be congruent if their three sides and three angles are equal.
Therefore, if two triangles have the same number of sides on each side, they are said to be congruent. Additionally, we can determine that they are congruent if we have a side, an angle between the sides, and then another side that is congruent, in that order: side, angle, side.
Let the given figure is a rectangle RSTU.
Since the all four angles of rectangle are of 90 degree.
So, each angle of rectangle RSTU is 90 degree.
Let, US divides the angle RUT and angle RST and form two new triangles, ΔSRU and ΔSTU.
Both the triangles having same measure of angles and sides.
⇒ ΔSRU ≅ ΔSTU
As the triangles are congruent so their sides are congruent.
Hence, RU is congruent to TS.
To know more about congruent triangles, click on the link
https://brainly.com/question/29789999
#SPJ1
Marcus bought a booklet of tickets to use at the amusement park. He used 25% of the tickets on rides, 1 2 of the tickets on video games, and the rest of the tickets in the batting cage. Marcus says he used 23% of the tickets in the batting cage. Do you agree? Complete the explanation.
Answers
Answer: Do not agree.
Step-by-step explanation:
To determine if we agree with Marcus, we need to verify if the percentages he used on rides, video games, and batting cage add up to 100%.
Marcus used 25% of the tickets on rides and 1/2 on video games. So, the total percentage of tickets he used is:
25% + 1/2 × 100% = 25% + 50% = 75%
This means that Marcus should have used 25% of the tickets in the batting cage. If he said he used 23% of the tickets in the batting cage, then we do not agree with him.
Which number line represents the solution to the inequality
1
+
2
x
<
−
7
?

Answers
Answer:
\(\boxed {x < -4}\) (Choice D)
Step-by-step explanation:
You first need to solve the following inequality in order to get the actual answer and find the actual graph:
\(1 + 2x < -7\)
-Subtract \(1\) to both sides:
\(1 - 1 + 2x < -7 - 1\)
\(2x < -8\)
-Divide both sides by \(2\):
\(\frac{2x}{2} < \frac{-8}{2}\)
\(\boxed {x < -4}\)
The number line graphed:

-2/3(3 2/3) I'm not sureeeee
Answers
Hope I helped!
During summer vacation,julie read 45 pages each day. her brother bret read 15 pages each day complete the tables to show how many pages each of them read after 5 days, what relationship do you notice between the terms and pattern?
Answers
After 5 days of summer vacation, Julie would have read 225 pages (45 pages x 5 days) and Bret would have read 75 pages (15 pages x 5 days). Therefore, ulie reads at a faster pace than Bret and both of their reading rates remain consistent over the course of 5 days.
Looking at the terms and pattern, we can see that Julie's daily reading rate is three times that of Bret's (45 pages compared to 15 pages). This means that Julie reads at a faster pace than Bret.
Additionally, we can see that both Julie and Bret's total number of pages read after 5 days is a multiple of their daily reading rate. Julie's total pages read is a multiple of 45 and Bret's total pages read is a multiple of 15. This shows that their daily reading rate is consistent over the 5 day period.
Overall, we can conclude that Julie reads at a faster pace than Bret and both of their reading rates remain consistent over the course of 5 days.
To know more about Vacation visit:
https://brainly.com/question/7593109
#SPJ11
1. The distance between two cities on the map was 6.5 cm. If the scale of the picture is 1:5000000, find the distance between the two cities.
2. How many centimeters can be used to represent a distance of 650 km on a map with a scale of 1:1500000?
3. If the distance between Ulaanbaatar and Choibalsan is 630 km, and the distance between these cities is shown on the map as 7 cm, find the scale of the map.
Answers
Considering the given scale, it is found that:
1. The distance between the two cities is of 325 km.
2. 43.3 cm should be used to represent the distance.
3. The scale of the map is of 1:9000000.
What is a scale?A scale is how much each unit in the drawing represents in actual distance.
For item 1, the scale of 1:5000000 means that each unit on the graph represents 5,000,000 units of actual distance.
The distance on the map is of 6.5 cm, hence the actual distance is of:
6.5 x 5000000 = 32,500,000 cm = 325 km.
For item 2, the scale is of 1:1500000, meaning that each cm of drawing is equivalent to 1,500,000 cm of real distance = 15 km.
Hence, the number of centimeters to represent a distance of 650 km is given by:
650/15 = 43.3 cm.
For item 3, we have that 7 cm represent 630 km = 63,000,000 cm, hence:
63,000,000/7 = 9000000.
Meaning that the scale is given by:
1:9000000.
More can be learned about scales at https://brainly.com/question/13036238
#SPJ1