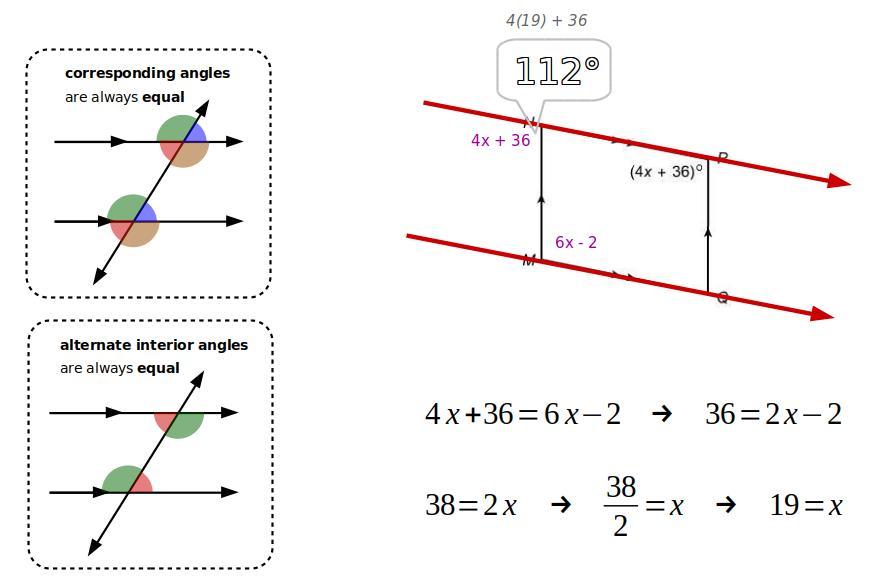
A research study variable that is believed to be related to the study's variable of interest is accurately described by each of the following terms except ___________.

3/2=1.5 hour=5400 second

Hope it helps you

Answer:

5,400 seconds.

The standard form of 5004200 is \(5.0042\times10^6\).

The standard form of a number is a way of writing the numbers in a form that follows a certain rule.

According to the given question.

We have a number 5004200.

The standard form of 5004200 is given by

\(5.0042\times10^6\)

Hence, the standard form of 5004200 is \(5.0042\times10^6\).

Find out more information about standard form of a number here:

brainly.com/question/13139379

Answer:The standard from of a number is introduced to avoid the difficulity of reading the large number

Step-by-step explanation:The given number is 50042000

5 million,4 thousands and 2 hundred in the standard form 5,004,200

el estudiante necesitará esperar aproximadamente 1.25 meses o alrededor de 1 mes y 8 días antes de su siguiente visita al peluquero.

Si el cabello corto crece a una tasa aproximada de 2 cm por mes, y el estudiante se cortó el cabello a un largo de 1 centímetro, podemos calcular cuánto tiempo llevará que el cabello crezca hasta los 3.5 centímetros.

La diferencia de longitud entre el largo actual del cabello y el largo deseado es de 3.5 cm - 1 cm = 2.5 centímetros.

Dado que el cabello crece a una tasa de 2 cm por mes, el tiempo requerido para que crezca 2.5 centímetros sería:

Tiempo = Longitud / Tasa de crecimiento

Tiempo = 2.5 cm / 2 cm/mes

Realizando la división, obtenemos:

Tiempo = 1.25 meses

Por lo tanto, el estudiante necesitará esperar aproximadamente 1.25 meses o alrededor de 1 mes y 8 días antes de su siguiente visita al peluquero.

For more such questions on esperar,click on

https://brainly.com/question/17382118

#SPJ8

\((\stackrel{x_1}{-1}~,~\stackrel{y_1}{-1})\hspace{10em} \stackrel{slope}{m} ~=~ - 4 \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-1)}=\stackrel{m}{- 4}(x-\stackrel{x_1}{(-1)}) \implies y +1= -4 (x +1) \\\\\\ y+1=-4x-4\implies {\LARGE \begin{array}{llll} y=-4x-5 \end{array}}\)

all sets are equal because all the sets contains only three elements in it that elements are 6,7,8

What is a set?

A set is a mathematical model for a collection of items; it comprises elements or members, which may be any mathematical object: numbers, symbols, points in space, lines, other geometrical structures, variables, or even other sets.

a = {6, 7, 8}

b = {x is in r| 5 ≤ x < 9}

c = {x is in r| 5 < x < 9}

d = {x is in z| 5 < x < 9}

e = {x is in z | 5 < x < 9}

Hence all sets are equal because all the sets contains only three elements in it that elements are 6,7,8

learn more about of sets here

https://brainly.com/question/13782700

#SPJ4

Equation of the line is -1/4x-5

From the question, we have

the given points (-8,-3) and (-12,-2) .

\(y-y_1=(y_2-y_1)/(x_2-x_1 ) (x-x_1 )\\y+3=(-2+3)/(-12+8)(x+8)\\y+3=1/(-4)(x+8)\\y=-1/4 x-2-3\\f(x)=-1/4 x-5\)

Slope:

A line's slope in mathematics is defined as the ratio of the change in the y coordinate to the change in the x coordinate.

Both the net change in the y-coordinate and the net change in the x-coordinate are denoted by y and x, respectively.

Consequently, the formula for the change in y-coordinate with respect to the change in x-coordinate is

m = y/x = y/x = change in y/change in x

where "m" represents a line's slope.

Slope, m = Change in y-coordinates/Change in x-coordinates

m = (y2 – y1)/(x2 – x1)

To learn more about slope visit: https://brainly.com/question/16180119

#SPJ9

Check the picture below.

Answer:

8 to 22

Step-by-step explanation:

if there are 22 people that have a pet whens there is 30 students in total, you have to do, 30-22, and 30-22=8 meaning there are 8 students who don't have pets.

And if already says 22 students have pets, therefore the answer is

8 to 22

8:22

Answer:

12.71 and

Step-by-step explanation:

The food truck sold 122 hamburgers that day.

Let's assume that x is the number of hamburgers that were sold that day..

A food truck sells hamburgers for 5.5 dollars each and drinks for 2 dollars each.

The food truck's revenue from selling a total of 203 hamburgers and drinks in one day was 834 dollars.

Now, as per the given conditions, x + y = 203 where y is the number of drinks sold that day.

The cost of a single hamburger is $5.5The cost of a single drink is $2

The revenue from the sale of 203 hamburgers and drinks is $834.

Thus, we can form another equation as 5.5x + 2y = 834So, we have to solve these two equations to find the value of x. Here, we will use the elimination method to solve the equations.

To eliminate y, we will multiply the first equation by 2, and we get:2x + 2y = 4065.5x + 2y = 834

Now, subtract the two equations:3.5x = 428x = 122

Hence, 122 hamburgers were sold that day.

Therefore, Total revenue = $834.

Number of hamburgers sold = x,

number of drinks sold = y.

We have the following system of equations:

                                x + y = 203 (1)

                                5.5x + 2y = 834 (2)

To solve the system, we will use the elimination method.

Multiplying equation (1) by 2, we get:2x + 2y = 4065.5x + 2y = 834

Now, subtracting equation (1) from equation (2), we get:3.5x = 428x = 122

Hence, the food truck sold 122 hamburgers that day.

Learn more about equation

brainly.com/question/29657983

#SPJ11

The most likely cause of the change in population mean in year 6 is an increase in the amount of land available, which allowed for an increase in the number of rabbits.

The most likely cause of the change in population size in year 6 shown in the graph is an increase in the amount of land available. The graph shows the population size of rabbits over different years, beginning at year 4 and ending at year 7. At the beginning of year 4, the population size of rabbits is 95, and the population size increases and decreases slightly through year 6. After year 6, the population size increases greatly, ending at 275. This suggests that there was an increase in the amount of land available, which allowed for an increase in the population size of rabbits. This increase in the available land could have been due to any number of factors, such as increased human settlement, a decrease in the number of predators, or improved access to food sources. All of these factors could have led to an increase in the number of rabbits, and the resulting change in population size in year 6.

Learn more about population mean here

https://brainly.com/question/19538277

#SPJ4

Answer:

C is the answerrrr

Step-by-step explanation:

The corresponding CDF is:F(x) = 1 - cos(x) for 0 < x < π/2F(x) = 1 for x ≥ π/2c. The expected value or mean of the given random variable X is 2. d. The variance of the given random variable X is π²/4 + 2π - 6.

The value of the constant A can be obtained by using the normalization condition that the integral of the PDF function over the entire possible range of X must be equal to 1. So, we can write the following integral to solve for

A:(∫f(x) dx) from 0 to π/2=∫A sin(x) dx= A [-cos(x)] evaluated at π/2 and 0= -A(cos(π/2) - cos(0))= A (1 - 0) =1. Therefore, the value of the constant A is 1. b. The CDF of the given random variable X is given as follows:

F(x)=∫f(x)dx from 0 to x, for 0 < x < π/2=∫sin(x) dx from 0 to x= [-cos(x)] evaluated at x and 0= -cos(x) - (-cos(0))= 1 - cos(x) for 0 < x < π/2=1 for x ≥ π/2. So, the corresponding CDF is as follows:

F(x) = 1 - cos(x) for 0 < x < π/2F(x) = 1 for x ≥ π/2c. The expected value or mean of the given random variable X can be obtained using the following formula:

E(X) = ∫xf(x)dx from 0 to π/2=∫x sin(x) dx from 0 to π/2= [-x cos(x)] evaluated at π/2 and 0 - ∫-cos(x) dx from 0 to π/2= -0 + cos(0) - ([-cos(x)] evaluated at π/2 and 0)= 0 + 1 - (-1)= 2. So, the expected value of the given random variable X is 2.

d. The variance of the given random variable X can be obtained using the following formula:

Var(X) = E(X²) - [E(X)]²=∫x² f(x)dx from 0 to π/2 - [E(X)]²=∫x² sin(x)dx from 0 to π/2 - (2)²= [-x² cos(x)] evaluated at π/2 and 0 + ∫2x cos(x)dx from 0 to π/2 - 4= -0 + π²/4 - 4 + (2 sin(x) + 2x cos(x)) evaluated at π/2 and 0= π²/4 - 2 - 4 + 2 + 2π= π²/4 + 2π - 6. So, the variance of the given random variable X is π²/4 + 2π - 6

Hence, the answer is: a. The value of the constant A is 1.b. The corresponding CDF is : F(x) = 1 - cos(x) for 0 < x < π/2F(x) = 1 for x ≥ π/2c. The expected value or mean of the given random variable X is 2. d. The variance of the given random variable X is π²/4 + 2π - 6

To know more about corresponding  visit:

brainly.com/question/31493107

#SPJ11

Answer:

1. The circle’s radius is approximately 14 cm.

2. The circle’s radius is approximately 7 cm.

3. The circle’s area is approximately  154 cm2

Question:a circled circumference is approximately 44cm

Complete each statement using one of these values : 7,11,14,22,88,138,154,196,380,616, Answers without letters: 1. 14cm  2. 7cm 3. 154 cm2

The number of arrangements of 6 balls with 2 red balls and 2 blue balls, we need to consider the number of ways to choose 2 red balls from the 4 available red balls and the number of ways to choose 2 blue balls from the 4 available blue balls.

These are both combinations, and we can use the formula for combinations to calculate them:

C(n, k) = n! / (k! (n-k)!).

For the red balls, C(4, 2) = 4! / (2! (4-2)!) = 6.

For the blue balls, C(4, 2) = 4! / (2! (4-2)!) = 6.

The total number of arrangements of 6 balls with 2 red balls and 2 blue balls is the product of the number of arrangements for each type of ball:

C(4, 2) * C(4, 2) = 6 * 6 = 36

So, there are 36 arrangements of 6 balls with 2 red balls and 2 blue balls.

For such more question on arrangements

https://brainly.com/question/1427391

#SPJ4

Answer:

x = 8°

y = 21°

Step-by-step explanation:

27 + 3y = 90

3y = 63

y = 21°

x + 8x + 18 = 90

9x = 72

x = 8°

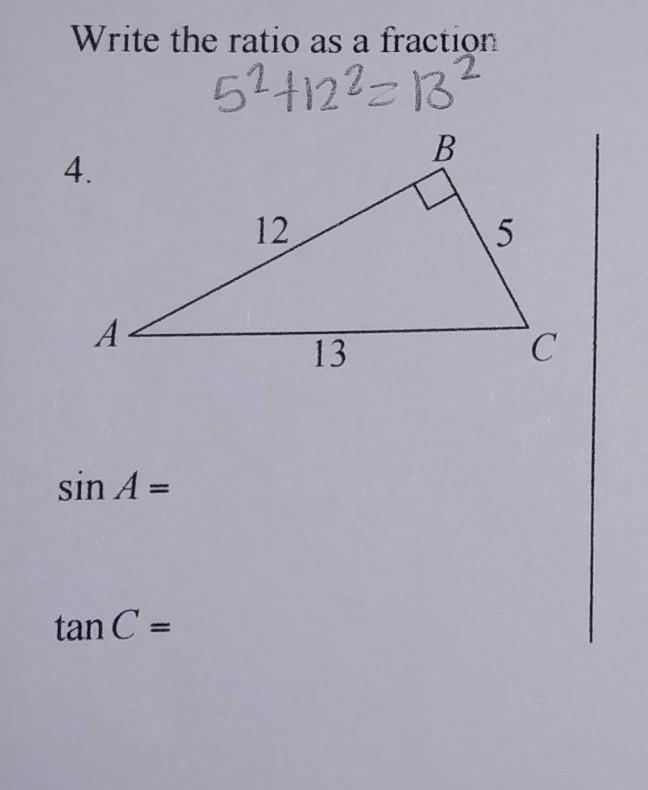
Answer:

Sin A = 5/13; tan C = 12/5

Step-by-step explanation:

Sin = opposite / hypotenuse. The opposite of A is 5, and the hypotenuse is 13, therefore Sin A = 5/13.

Tan = opposite / adjacent. The opposite of C is 12, and the adjacent is 5, so tan C = 12 / 5

Answer:

\(5\frac{1}{4}\)

Step-by-step explanation:

\(3\frac{1}{2} *1\frac{1}{2}\)

3*2+1/2 * 2*1+1/2

7/2 * 3/2

7*3/2*2

21/4

\(5\frac{1}{4}\)

Based on the given information, the function g has a domain of -18 ≤ x ≤ 13.9 and a range of -10 ≤ g(x) ≤ 6.

The given information provides details about the function g's values at specific points, as well as the domain and range of the function. Let's break down the solution based on the given information:

1. Domain:

The domain of the function g is determined by the range of values of x for which the function is defined. According to the given information, the domain is -18 ≤ x ≤ 13.9.

2. Range:

The range of the function g is determined by the range of values of g(x) for the corresponding values of x within the defined domain. According to the given information, the range is -10 ≤ g(x) ≤ 6.

3. Specific Function Values:

We are also given specific values of the function g at x = 4 and x = -3. We know that g(4) = 1 and g(-3) = -10. These values provide additional information about the behavior of the function at those points.

In summary, based on the given information, the function g has a domain of -18 ≤ x ≤ 13.9, indicating the range of valid input values. The range of the function g is -10 ≤ g(x) ≤ 6, indicating the range of output values. Additionally, the function values g(4) = 1 and g(-3) = -10 provide specific information about the behavior of the function at those points.


To learn more about function click here: brainly.com/question/28599653

#SPJ11

The equation is separable. The solution to the initial value problem is y(t) = e^(4 * e^t) , therefore option A is correct.

To determine whether the given equation is separable and solve the initial value problem:

We will follow these steps:

STEP 1: Identify the given differential equation: y'(t) = 4y * e^t
STEP 2: Rewrite the equation in terms of dy/dt: dy/dt = 4y * e^t
STEP 3:Rearrange the terms to separate variables: (1/y) dy = 4 * e^t dt
STEP 4:Integrate both sides: ∫(1/y) dy = ∫4 * e^t dt
STEP 5:Evaluate the integrals: ln|y| = 4 * e^t + C1 (we can drop the absolute value since y > 0)
STEP 6:Solve for y: y = e^(4 * e^t + C1)
STEP 7:Apply the initial condition y(0) = 1: 1 = e^(4 * e^0 + C1)
STEP 8:Solve for C1: C1 = 0
STEP 9:Substitute C1 back into the solution: y(t) = e^(4 * e^t)

The equation is separable. The solution to the initial value problem is y(t) = e^(4 * e^t) (Type an exact answer in terms of e).

To know more about Separable:

https://brainly.com/question/27928263

#SPJ11

The perimeter or circumference is 42 ft and area is 68 ft.

From the figure:

The figure represents a rectangle so opposite sides are equal.

Length l = 17 ft

width w = 4 ft

we know that:

Perimeter of rectangle = 2(l+w)

= 2(17+4)

= 2*21

= 42 ft

Area of rectangle = l*w

= 17*4

= 68 ft.

Learn more about the rectangle here:

https://brainly.com/question/15019502

#SPJ1

When we express the equation 2x - y = 12 in slope intercept form, the result obtained is y = 2x - 12 (2nd option)

The slope intercept form for an equation is written as illustrated below:

y = mx + c

Where

With the above information, we can obtain the slope intercept form of the equation. Details below:

2x - y = 12

Rearrange to make y the subject of the expression, we have

2x = 12 + y

y = 2x - 12

Thus, we can conclude that the equation in the slope intercept form is

y = 2x - 12 (2nd option)

Learn more about coordinate geometry:

https://brainly.com/question/21298390

#SPJ4

Complete question:

Given the equation 2x - y = 12, which equation is written in slope intercept form?

y = -2x + 12

y = 2x - 12

y = 2x + 12

y = -2x - 12

Answer:

you didn't add options for the sentences, but

x-5 =-10 (add 5 to both sides to get x alone)

x= -5

so anything that has to do with x equaling - 5 would be correct

after reading through the sentences, the correct answer is:

a number subtracted from five is equal to negative ten

because that sentence is saying " 5 - n = - 10 " and that's not what's happening

Step-by-step explanation:

the 81% confidence interval for the average iron level of the sample is approximately 2.605 to 4.323.

To find the 81% confidence interval for the average iron level of a sample of 12 men, we can use the formula:
Confidence Interval = Sample Mean ± (Critical Value × Standard Error)
First, we need to calculate the critical value. Since the sample size is small (n < 30), we'll use a t-distribution. For an 81% confidence level with 12 degrees of freedom (n - 1), the critical value is approximately 1.372.
Next, we calculate the standard error using the formula:
Standard Error = Standard Deviation / √(Sample Size)
In this case, the standard deviation is 2.04 and the sample size is 12, so the standard error is approximately 0.589.
Now we can plug these values into the confidence interval formula:
Confidence Interval = 3.464 ± (1.372 × 0.589)
Calculating the upper and lower limits:
Upper Limit = 3.464 + (1.372 × 0.589) ≈ 4.323
Lower Limit = 3.464 - (1.372 × 0.589) ≈ 2.605

To know more about average visit:

brainly.com/question/14543163

#SPJ11

We need to calculate the 8% of $45

The total charge will be

ANSWER

The total charge is $48.60

Answer:

$1,061.21

Step-by-step explanation:

According to the scenario, computation of the given data are as follows,

Present value (PV) = $1,000

Rate of interest compounded yearly (r) = 2%

Time period (n) = 3

So, we can calculate the future value (FV) by using following formula,

Future Value = PV(1 + r)^n

By putting the value, we get

FV = $1,000 ( 1 + 0.02)^3

= $1,000 ( 1.02)^3

= $1,000 ( 1.061208)

= $1,061.21

Answer:

The line x + y = 6 can be written in slope-intercept form (y = mx + b) by solving for y:

y = -x + 6

So the slope of this line is -1.

Since the line we want is parallel to this line, it must also have a slope of -1.

Now we can use the point-slope form of a line to find the equation of the line we want:

y - y1 = m(x - x1)

where m is the slope and (x1, y1) is the given point.

Plugging in the values we know, we get:

y - 8 = -1(x - (-4))

Simplifying:

y - 8 = -x - 4

y = -x + 4

So the equation of the line that passes through the point (-4, 8) and is parallel to the line x + y = 6 is y = -x + 4.

The distribution of IQ is approximately normal in shape with a mean of 100 and a standard deviation of 20. According to the standard deviation rule, 95% of people have an IQ between 60 and 140.

The IQ distribution follows a normal distribution, also known as a bell curve, with a mean of 100 and a standard deviation of 20. This means that the majority of individuals fall close to the average IQ score of 100, and the further away from the mean, the fewer people there are with those IQ scores.

The standard deviation rule, also known as the empirical rule or the 68-95-99.7 rule, is a statistical guideline for normal distributions. It states that approximately 68% of values fall within one standard deviation of the mean, approximately 95% fall within two standard deviations, and approximately 99.7% fall within three standard deviations.

In this case, we are interested in the percentage of people who have an IQ between 60 and 140. Since the mean is 100 and the standard deviation is 20, we can calculate the distance from the mean to each boundary as follows:

Lower boundary: (60 - 100) / 20 = -2 standard deviations

Upper boundary: (140 - 100) / 20 = 2 standard deviations

According to the standard deviation rule, approximately 95% of values fall within two standard deviations of the mean. Therefore, approximately 95% of people have an IQ between 60 and 140.

Learn more about the Standard deviation rule

brainly.com/question/8466426

#SPJ11

Answer:

A, \(\sqrt{17}\)

Step-by-step explanation:

a^2 + b^2 = c^2

8^2 + b^2 = 9^2

64 + b^2 = 81

b^2 = 17

b = \(\sqrt{17}\)

Answer:

by pythagoras theorem

9² = 8² + x²

x² = 81 - 64

x² = 17

x = root 17

option A

Answer: You add 4+2/5 then multiply it times 2.5

Step-by-step explanation:

If you Evaluate it your answer will be: 11 = -13