A study found that 8% of dog owners brush their dog's teeth. Of 25 dog owners, about how many would be expected to brush their dog's teeth? *
10 points
(1) 8
(2) 25
(3) 2
(4) 17
Answers
Related Questions
Write an exponential function f so that the slope of a line from the point (0, f(0)) to the point (2, f(2)) is equal to 12.
Answers
The exponential function f so that the slope of a line from the point (0, f(0)) to the point (2, f(2)) is equal to 12 is defined as follows:
f(x) = 5^x.
How to define the exponential function?The general format of an exponential function is given as follows:
y = ab^x.
In which:
a is the initial value.b is the rate of change.The slope of a line, given two points, is given by the division of the change in the output by the change in the input of these two points.
Considering that the slope of points (0, f(0)) and (2, f(2)) is equals to 12, we have that:
[f(2) - f(0)]/(2 - 0) = 12
f(2) - f(0) = 24.
One case that satisfies this involves these two following points.
(0,1) -> f(0) = 1.(2,25) -> f(2) = 25.Hence the parameter a is given as follows:
a = 1.
When x = 2, y = 25, meaning that the parameter b is calculated as follows:
b² = 25
b = 5.
Hence the exponential function is:
f(x) = 5^x.
More can be learned about exponential functions at https://brainly.com/question/25537936
#SPJ1
The sum of two numbers is 8. The difference of the same two numbers is 4. What are the two numbers?
Answers
Answer:
2 and 6
Step-by-step explanation:
2+6=8. 6-2=4.
Answer:
2 and 6
Step-by-step explanation:
What is the missing angle?

Answers
3x + 27 =180
-27
3x = 153
÷3
x = 51
a=142
(vertically opposite angles are equal)
Reflex angles adds up to 360
360 - (142x2) = 76
76/2 = 38
t & c = 38
Hope this helps!
Answer:
Here you go :) if you need anything tell me!

Geometry. Math nation section 3

Answers
∠g and ∠h are complementary angles and ∠g and ∠h are acute angles are true statements from the given information
Two angles are given.
∠g = (2x-90)°
∠h = (180-2x)°
We have to find the statement which is true about the angles g and h.
If both angles are greater than zero.
Complementary angles add up to 90 degrees
i.e., ∠g and ∠h are complementary if ∠g + ∠h = 90°.
Substituting the given values:
∠g + ∠h
= (2x-90)° + (180-2x)° = 90°
Thus, ∠g and ∠h are complementary angles.
and both the angles are less than 90 degrees so we can tell that angles ∠g and ∠h are acute.
So the statement ∠g and ∠h are acute angles is also true
Hence, ∠g and ∠h are complementary angles and ∠g and ∠h are acute angles are true statements
To learn more on Angles click:
https://brainly.com/question/28451077
#SPJ1
4.364923697 in radical form
Answers
Answer:
i hope u can round other wise its this 4 3649237 / 10000000
Step-by-step explanation:
the dash is the fraction symbol
Use the method of this example to calculate f · dr,c wheref(x, y) = 2xyi (y2 − x2)j(x2 y2)2 and c is any positively oriented simple closed curve that encloses the origin. f · dr
Answers
The area around the given curve according to the green theorem is \(F. dr = 0\).
According to the statement
we have to find the area enclosed by the simple closed curve that encloses the origin.
So, We know that the
The given equation is
\(f(x,y) = \frac{2xyi + (y^{2} - x^{2} ) j}{(x^{2} + y^{2} )^{2} }\)
and
If function is in form of,
\(F = Pi + Qj\)
and C is any positively oriented simple closed curve that encloses the origin.
Then,by use of Green's theorem
Do the partial differentiation of the given function
Then
\(\frac{dQ}{dx} = \frac{2x^{3} - 6xy^{2}}{(x^{2} + y^{2} )^{3}}\)
and
\(\frac{dP}{dy} = \frac{2x^{3} - 6xy^{2}}{(x^{2} + y^{2} )^{3}}\)
On substitution in Green's theorem,
We get the value
\(F. dr = 0\)
From this it is clear that the area around the given curve is zero.
So, The area around the given curve according to the green theorem is \(F. dr = 0\).
Learn more about Green theorem here
https://brainly.com/question/23265902
#SPJ4
is y=1/2x+10 a linear equation
Answers
A grocery store has only one checkout counter. Customers arrive at this checkout at random from 1 to 8 minutes apart Each possible value of inter-arrival time has the same probability of occurrence as given below. Analyze the system by simulating the arrival of 20 customers using the random numbers 913, 727, 15, 948, 309, 922, 753, 235, 302, 109, 93, 607, 738, 359, 888, 106, 212, 493 and 535. Also, calculate the average time between arrival.
Distribution of time between arrivals
Time Arrivals (Minutes) Probability
1 0.125
2 0.125
3 0.125
4 0.125
5 0.125
6 0.125
7 0.125
8 0.125
Answers
Therefore, the average time between arrivals is approximately 2.421 minutes.
To simulate the arrival of 20 customers and calculate the average time between arrivals, we will use the given random numbers and the probabilities associated with each possible inter-arrival time.
Here's how we can proceed:
Initialize variables:
Set the initial time to 0.
Create an empty list to store the arrival times.
Iterate 20 times for each customer:
Generate a random number between 0 and 1.
Determine the inter-arrival time based on the random number and the given probabilities.
Add the inter-arrival time to the current time to get the arrival time for the customer.
Append the arrival time to the list of arrival times.
Update the current time to the arrival time.
Calculate the average time between arrivals:
Compute the difference between each consecutive arrival time.
Sum up all the differences.
Divide the sum by the total number of differences (19 in this case) to get the average time between arrivals.
Using the given random numbers 913, 727, 15, 948, 309, 922, 753, 235, 302, 109, 93, 607, 738, 359, 888, 106, 212, 493, and 535, we can proceed with the simulation.
Here is the step-by-step calculation:
Initialize variables:
Initial time: 0
List of arrival times: []
Iterate 20 times for each customer:
For each random number, calculate the corresponding inter-arrival time based on the probabilities:
For 913: inter-arrival time = 3 (probability of 0.125 for 3 minutes)
For 727: inter-arrival time = 2 (probability of 0.125 for 2 minutes)
For 15: inter-arrival time = 1 (probability of 0.125 for 1 minute)
For 948: inter-arrival time = 3 (probability of 0.125 for 3 minutes)
For 309: inter-arrival time = 2 (probability of 0.125 for 2 minutes)
For 922: inter-arrival time = 3 (probability of 0.125 for 3 minutes)
For 753: inter-arrival time = 3 (probability of 0.125 for 3 minutes)
For 235: inter-arrival time = 2 (probability of 0.125 for 2 minutes)
For 302: inter-arrival time = 2 (probability of 0.125 for 2 minutes)
For 109: inter-arrival time = 1 (probability of 0.125 for 1 minute)
For 93: inter-arrival time = 1 (probability of 0.125 for 1 minute)
For 607: inter-arrival time = 2 (probability of 0.125 for 2 minutes)
For 738: inter-arrival time = 3 (probability of 0.125 for 3 minutes)
For 359: inter-arrival time = 2 (probability of 0.125 for 2 minutes)
For 888: inter-arrival time = 3 (probability of 0.125 for 3 minutes)
For 106: inter-arrival time = 1 (probability of 0.125 for 1 minute)
For 212: inter-arrival time = 2 (probability of 0.125 for 2 minutes)
For 493: inter-arrival time = 3 (probability of 0.125 for 3 minutes)
For 535: inter-arrival time = 3 (probability of 0.125 for 3 minutes)
Calculate the arrival time for each customer:
Arrival time for customer 1: 0 + 3 = 3
Arrival time for customer 2: 3 + 2 = 5
Arrival time for customer 3: 5 + 1 = 6
Arrival time for customer 4: 6 + 3 = 9
Arrival time for customer 5: 9 + 2 = 11
Arrival time for customer 6: 11 + 3 = 14
Arrival time for customer 7: 14 + 3 = 17
Arrival time for customer 8: 17 + 2 = 19
Arrival time for customer 9: 19 + 2 = 21
Arrival time for customer 10: 21 + 1 = 22
Arrival time for customer 11: 22 + 1 = 23
Arrival time for customer 12: 23 + 2 = 25
Arrival time for customer 13: 25 + 3 = 28
Arrival time for customer 14: 28 + 2 = 30
Arrival time for customer 15: 30 + 3 = 33
Arrival time for customer 16: 33 + 1 = 34
Arrival time for customer 17: 34 + 2 = 36
Arrival time for customer 18: 36 + 3 = 39
Arrival time for customer 19: 39 + 3 = 42
Arrival time for customer 20: 42 + 3 = 45
Append the arrival times to the list: [3, 5, 6, 9, 11, 14, 17, 19, 21, 22, 23, 25, 28, 30, 33, 34, 36, 39, 42, 45]
Calculate the average time between arrivals:
Calculate the differences between consecutive arrival times:
Difference 1: 5 - 3 = 2
Difference 2: 6 - 5 = 1
Difference 3: 9 - 6 = 3
Difference 4: 11 - 9 = 2
Difference 5: 14 - 11 = 3
Difference 6: 17 - 14 = 3
Difference 7: 19 - 17 = 2
Difference 8: 21 - 19 = 2
Difference 9: 22 - 21 = 1
Difference 10: 23 - 22 = 1
Difference 11: 25 - 23 = 2
Difference 12: 28 - 25 = 3
Difference 13: 30 - 28 = 2
Difference 14: 33 - 30 = 3
Difference 15: 34 - 33 = 1
Difference 16: 36 - 34 = 2
Difference 17: 39 - 36 = 3
Difference 18: 42 - 39 = 3
Difference 19: 45 - 42 = 3
Sum up all the differences: 2 + 1 + 3 + 2 + 3 + 3 + 2 + 2 + 1 + 1 + 2 + 3 + 2 + 3 + 1 + 2 + 3 + 3 + 3 = 46
Divide the sum by the total number of differences: 46 / 19 = 2.421
To know more about average time,
https://brainly.com/question/14521655
#SPJ11
Find the indicated one-sided limits, if they exist. (if an answer does not exist, enter dne.)
Answers
The limit doesn't exist.
What is a limit?
The value that a function (or sequence) approaches when the input (or index) gets closer to a particular value is known as a limit. Calculus and mathematical analysis are impossible without limits, which are also required to determine continuity, derivatives, and integrals.
In addition to being closely related to limit and direct limit in category theory, the idea of a limit of a sequence is further generalized to include the concept of a limit of a topological net.
A function's limit is typically expressed in formulas as
\(\lim_{x \to c } F(x) = L\)
It is typically used to assign values to specific functions at locations where none are defined while maintaining consistency with existing values.
\(F(x) = -x+8 ,x\leq 0\)
\(F(x) = 4x+9 , if x > 0\)
\(\lim_{x \to 0^{+} } F(x) = \lim_{n \to 0^{+} } (4x+9) = 9\)
\(\lim_{x \to 0^{-} } F(x) = \lim_{x \to 0^{-} } (-x+8) =8\)
\(\lim_{x \to 0^{+} } F(x) \neq \lim_{x \to 0^{-} } F(x)\)
So limit doesn't exist
For limit to exist
\(\lim_{x \to 0^{+} } F(x) = \lim_{x \to 0^{-} } F(x) = \lim_{x \to 0} f(x)\)
must be satisfied
To learn more about Limit, visit:
https://brainly.com/question/24067291
#SPJ4
The product of this number and 10 is equal to the square of this number
Answers
Answer:
___ x 10 = ____^2
Step-by-step explanation:
what do u need to know in order to find velocity
Answers
Answer:
you need to divide the distance by the time it takes to travel that same distance, then you add your direction to it.
Step-by-step explanation:
Candice has a dog walking business. It takes her 40 minutes to complete her route with 2 dogs. For each additional dog walked at the same time, it takes her 5 more minutes to complete her route. If x represents the total number of dogs she walks at the same time, which of the following equations can be used to find out how long it takes Candice to complete her route?
A. y = 40x + 5
B. y = 5(x - 2) + 40
C. y = 5x + 40
D. y = 40(x - 2) + 5
Answers
Answer:
The answer is B
Step-by-step explanation:
Candice takes 40 minutes to walk two dogs and B is the only equation that lets you get 40 minutes when x equals 2 dogs
Determine if line AB is tangent to the circle.

Answers
Answer:
Is a tangent
Step-by-step explanation:
~ By definition, a tangent to circle is a straight line, presently perpendicular to a radius if one. In this case tangent AB should be perpendicular to the radius. If we were to call the center O, we would say AB should be perpendicular to OA. ~
1. Now let us say at the moment that AB is a tangent. If that is so, it should be that m∠A = 90 degrees ( ° ), provided AB is ⊥ to OA by definition.
2. Now the triangle ABO is a right triangle, and with that is should be that Pythagorean Theorem is applied. This can help us prove if AB is a tangent or not. If Pythagorean Theorem is not applicable it would mean ABO is not a right angle triangle, that AB is not ⊥ to OA, and thus can't be a tangent.
3. Let us say x ⇒ side OA, and that side BO = 9 + 8 + 17:
AB^2 + OA^2 = BO^2,
15^2 + x^2 = 17^2,
x = 8
4. Now there are two radii present, OA is only one of them. As radii are ≅, OA = other radii, 8 = 8
5. This proves that Pythagorean Theorem is applicable, that ABO is a right triangle, that m∠A = 90°, and that by definition AB is a tangent
* I have already answered this question before *
Two irrational numbers that equal to 2. What are they?
Answers
The two irrational numbers that sum up to 2 are (√5 - 2) and (4 - √5)
What are irrational numbers?Irrational numbers are numbers that cannot be expressed or written as a quotient of integers.
Example of irrational numbers are; √5 , √7, √3, etc
Irrational numbers that can add up to 2
(√5 - 2) + (4 - √5)
expand the bracket
√5-2 + 4-√5
collect like terms
√5 - √5 -2 + 4
-2 + 4
2
Hence, the two irrational numbers that sum up to 2 are (√5 - 2) and (4 - √5)
Learn more about irrational numbers here:
https://brainly.com/question/20400557
#SPJ1
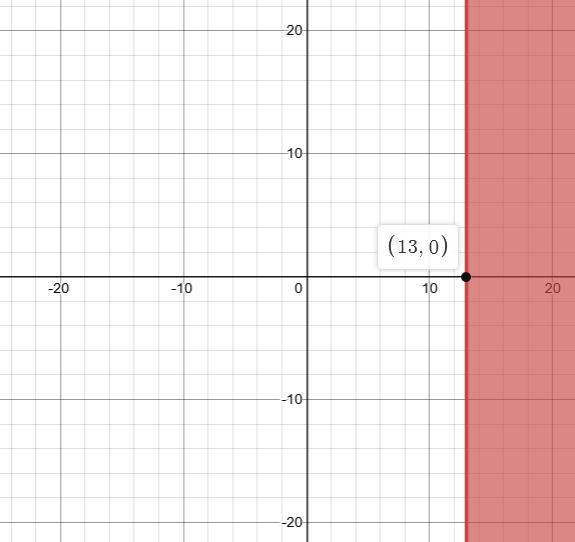
thx in advance for the help

Answers
Answer: \(x\geq 13\)
Step-by-step explanation:
Given
The inequality is \(2x-7\geq 19\)
adding both side 7
\(2x-7+7\geq 19+7\\2x\geq 26\)
Multiply both sides by \(\frac{1}{2}\)
\(\dfrac{1}{2}\times 2x\geq 26\times \dfrac{1}{2}\\\\x\geq 13\)
the shaded region in the figure indicates the solution set.
the surface area of a sphere is 110.25 sqaure feet .find the diameter of the shpere

Answers
Mrs. Buchanan gave her two daughters $5 to share equally at the carnival. How much money will each daughter have to spend?
Answers
Answer: $2 and 5 cents each
Step-by-step explanation:
Each daughter will equally split up the 5 dollars, so 5 divided by 2, you will get 2.5
ALGEBRA Simplify 4(3 x-2)(2 x+4)+3x² + 5x-6
F 9x² + 3x - 14
H 27x² + 37x - 38
G 9x² + 13x - 14
J 27x² + 27x - 26
Answers
The simplified form of the given equation 4(3x-2)(2x+4) +\(3x^{2}\) + 5x - 6 is \(27x^{2} + 37x - 38\).
The branch of mathematics that deal with the study of mathematical symbols and the rules for manipulating those symbols is known as Algebra. Elementary Algebra, Abstract Algebra, Advanced Algebra, Linear Algebra, and Commutative Algebra are sub-branches of Algebra.
Algebra forms the basis for advanced studies in many fields, including science, mathematics, medicine, engineering, and economics.
The given equation is 4(3x-2)(2x+4) +\(3x^{2}\) + 5x - 6. The step wise simplification of this algebraic equation is as follows :
4(3x-2)(2x+4) +\(3x^{2}\) + 5x - 6
= (12x - 8)(2x+4) +\(3x^{2}\) + 5x - 6
= \(24x^{2} - 16x + 48x - 32 + 3x^{2} + 5x -6\)
= \(27x^{2} + 37x -38\)
The simplified form of the given equation 4(3x-2)(2x+4) +\(3x^{2}\) + 5x - 6 is \(27x^{2} + 37x - 38\).
To know more about Algebraic Expressions refer to the link:
https://brainly.com/question/4344214
#SPJ4
Using R, construct and store a 4 x 2 matrix that is filled row-wise with the following values: 4.3, 3.1, 8.2, 9.2, 3.2, 0.9, 1.6, and 6.5, in that order. Using R, overwrite the second column of the matrix you have created in Q6 with the following numbers: 8, 9, 11, and 17 in that order. Save your updated matrix to an object named BruceLee.
Answers
To construct and store a 4 x 2 matrix filled row-wise with the given values in R, you can use the following code:
# Create the matrix
myMatrix <- matrix(c(4.3, 3.1, 8.2, 9.2, 3.2, 0.9, 1.6, 6.5), nrow = 4, ncol = 2, byrow = TRUE)
This code creates a matrix called "myMatrix" with 4 rows and 2 columns, filled row-wise with the provided values.
To overwrite the second column of the matrix with the numbers 8, 9, 11, and 17 in that order, you can use the following code:
# Overwrite the second column
myMatrix[, 2] <- c(8, 9, 11, 17)
This code selects the second column of the matrix using the indexing notation [, 2] and assigns the new values using the c() function. The second column is replaced with the numbers 8, 9, 11, and 17.
Finally, to save the updated matrix to an object named "BruceLee", you can use the following code:
# Save the updated matrix
BruceLee <- myMatrix
Now the updated matrix with the overwritten second column is stored in the object "BruceLee" for further use.
Learn more about indexing notation here:
brainly.com/question/15521685
#SPJ11
Please, let me get the answers in 15 mins. Explain what a
strategy canvas is and how it is used
Answers
A strategy canvas is a visual framework used to analyze and compare the strategic positioning of different companies or products within an industry.
It is a tool developed by W. Chan Kim and Renée Mauborgne, the creators of the Blue Ocean Strategy, to help organizations identify and create new market spaces by differentiating their offerings.
The strategy canvas consists of two axes: the horizontal axis represents the key factors that the industry competes on, and the vertical axis represents the offering level or degree of offering provided for each factor. By plotting the current state of competing products or companies on the canvas, organizations can gain insights into the competitive landscape and identify areas of opportunity for innovation and differentiation.
The strategy canvas helps visualize the competitive factors that are driving the industry and highlights areas of convergence or similarity among existing offerings. It allows organizations to identify untapped market spaces where they can create unique value propositions and redefine the competitive boundaries.
To use a strategy canvas effectively, organizations need to analyze the key factors that customers value in the industry and assess the relative performance of their offerings compared to competitors. By identifying the factors where they are underperforming and overperforming, organizations can focus on enhancing their value proposition by reallocating resources, investing in areas of differentiation, and eliminating or reducing elements that do not create significant customer value.
A strategy canvas is a powerful tool for strategic analysis and innovation. It helps organizations visualize the competitive landscape, identify areas for differentiation, and create new market spaces by providing a clear understanding of customer preferences and the competitive factors that drive industry success.
Learn more about differentiating here:
https://brainly.com/question/24898810
#SPJ11
Find the points on the ellipse 64x² + y² = 64 that are farthest away from the point (1.0). List them as a list of points, such as "(1.2).(3,4)". List of points :
Answers
The points on the ellipse 64x² + y² = 64 that are farthest away from the point (1,0) is the list of points: (-1, 0) and (3, 0).
1. First, rewrite the equation of the ellipse in standard form: (x² / 1) + (y² / 64) = 1.
2. Use the distance formula between points (x, y) and (1, 0): D = √((x - 1)² + y²).
3. To maximize D, maximize D²: F(x, y) = (x - 1)² + y².
4. Use the constraint of the ellipse equation to substitute y²: F(x, y) = (x - 1)² + 64(1 - x²).
5. Differentiate F(x, y) with respect to x and set it to 0: dF/dx = -4x³ + 4x² + 4x - 4 = 0.
6. Solve the cubic equation: x ≈ -1, 1, 3 (discard x = 1 as it's the given point).
7. Substitute the x values back into the ellipse equation to find the corresponding y values: y² = 64 - 64x².
8. For x = -1 and x = 3, y² = 0, which means y = 0.
9. The farthest points are (-1, 0) and (3, 0).
To know more about distance formula click on below link:
https://brainly.com/question/25841655#
#SPJ11
O is the center of a regular nonagon with a radius of 19. Find its perimeter. Round to the nearest tenth if necessary.
Answers
The perimeter of the regular nonagon with a radius of 19 is 58.3 units.
How do we calculate?The nonagon's center, designated by the letter O, has a radius of 19; the distance from O to any vertex is therefore equal to the radius:
sin(20) = s / 19
We then solve for s:
s = 19 * sin(20)
s = 6.4807
We find the length of one side by multiplying it by 9:
Perimeter = 9 * s
perimeter= 9 * 6.4807
perimeter = 58.3263
In conclusion, a nonagon is described as a nine sided polygon and it is also called an Enneagon or 9-gon.
Learn more about nonagon at:
https://brainly.com/question/30193360
#SPJ1
in an isosceles triangle two sides are equal. the third side is 2 less than twice the length of the sum of the two sides. the perimeter is 40. what are the lengths of the 3 sides
Answers
Answer:
s for length of either equal side
b for the unequal side
b=-2+2*(s+s) and 2s+b=40
b=2*2s-2
b=4s-2
2s+4s-2=40
6s-2=40
6s=42
s=7
b=4*7-2
b=28-2
b=26
Blank divided by 10 =800
Answers
Answer:
(8,000/10)=800
What is the equation of this line?
A: y=-2x
B: y = ½x
C: y = -½x
D: y = 2x

Answers
Answer:
D
Step-by-step explanation:
when x=1, y should = 2
2(1)=2
so y=2x is correct
what is the distance between these points
(1,-2),(9,13)
Answers
Answer:
17 units
Step-by-step explanation:
calculate the distance d using the distance formula
d = \(\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2 }\)
with (x₁, y₁ ) = (1, - 2 ) and (x₂, y₂ ) = (9, 13 )
d = \(\sqrt{(9-1)^2+(13-(-2))^2}\)
= \(\sqrt{8^2+(13+2)^2}\)
= \(\sqrt{64+15^2}\)
= \(\sqrt{64+225}\)
= \(\sqrt{289}\)
= 17
Instructions: Find the missing side of the triangle.
48
50

Answers
Answer:
x = 14
Step-by-step explanation:
Since this is a right triangle, we can use the Pythagorean theorem
a^2 + b^2 = c^2 where a and b are the legs and c is the hypotenuse
48 ^2 + x^2 = 50^2
2304+x^2=2500
x^2 = 2500-2304
x^2 =196
Taking the square root of each side
sqrt(x^2) = sqrt(196)
x = 14
Answer:
14
Step-by-step explanation:
Use A^2+B^2=C^2
A=48
C=50
So B=sqrt(C^2-A^2)
B=sqrt(50^2-48^2)
B=sqrt(2500-2304)
B=sqrt(196)
B=14
To solve the equation below by completing the square, what is your first step?
3x2 + 18x = 21
Add 9 to each side of the equation.
Divide both sides of the equation by 3
Multiply both sides of the equation by 3
Add 81 to each side of the equation.
Answers
Step-by-step explanation:
well, for that I want the equation as simple a possible. especially do I want to have a pure "x²" term with "1" as the factor.
so, as I see that all terms in the equation are multiples of 3, my first step will be to divide both sides by 3.
leading to
x² + 6x = 7
Answer:
Answer:
The first step to solve the equation by completing the square 3x²+ 18x= 21 is multiply both sides of the equation by .
The factors of the equations 3x²+ 18x= 21 are 1 ,-7 .
Step-by-step explanation:
As given the equations
3x² + 18x = 21
Multiply both sides of the equation by .
Thus the equation becomes
Simplify the above
x² + 6x = 7
Adding 9 on both sides of the above equation
x² + 6x + 9 = 7 + 9
x² + 6x + 9 = 16
(As (a +b)² = a² + b² + 2ab
Thus (x+3)² = x² + 6x + 9 )
Put in the above
(x+3)² = 16
Taking square root on both side
√16 = ± 4
First take
(x + 3) = 4
x = 4 -3
x = 1
Second take
(x+ 3) = -4
x = - 4 -3
x = -7
Therefore the first step to solve the equation by completing the square 3x²+ 18x= 21 is multiply both sides of the equation by .
The factors of the equations 3x²+ 18x= 21 are 1 ,-7 .
how to know if a function has a vertical asymptote
Answers
To determine if a function has a vertical asymptote, you need to consider its behavior as the input approaches certain values.
A vertical asymptote occurs when the function approaches positive or negative infinity as the input approaches a specific value. Here's how you can determine if a function has a vertical asymptote:
Check for restrictions in the domain: Look for values of the input variable where the function is undefined or has a division by zero. These can indicate potential vertical asymptotes.
Evaluate the limit as the input approaches the suspected values: Calculate the limit of the function as the input approaches the suspected values from both sides (approaching from the left and right). If the limit approaches positive or negative infinity, a vertical asymptote exists at that value.
For example, if a rational function has a denominator that becomes zero at a certain value, such as x = 2, evaluate the limits of the function as x approaches 2 from the left and right. If the limits are positive or negative infinity, then there is a vertical asymptote at x = 2.
In summary, to determine if a function has a vertical asymptote, check for restrictions in the domain and evaluate the limits as the input approaches suspected values. If the limits approach positive or negative infinity, there is a vertical asymptote at that value.
know more about vertical asymptote.
https://brainly.com/question/29260395
#SPJ11
in a starch analysis, a magazine ad for absolute vodka received a score of 140. what does this mean?
Answers
There are 5 possibilities:
a. That particular ad scored 140 percent above comparable ads.
b. That particular ad scored 40 percent above comparable ads.
c. The percentage of respondents who read half or more of the written material in the ad was 40 percent.
d. The percentage of respondents who recalled seeing the ad was 40 percent.
e. That particular ad is capable of generating market share gains of 40 percent.
The purpose of the Starch Service is to report to what extent a client's magazine advertisements are seen and read. Using Starch, a client can compare the readership of current advertisements with past advertisements, or competitors advertisements. One use for the service is that it provides information as to how advertisements can be presented so that readership can be increased by the manipulation of various elements of magazine advertising included in the reports.
The answer is option (b): That particular ad scored 40 percent above comparable ads.
To learn more about market, visit the link:
brainly.com/question/13414268
#SPJ4