A survey found that 11 out of 100 randomly selected people had a pet lizard. On the basis of this survey, how many people in a group of 1,300 people are likely to have a pet lizard? a) 143 people b) 90 people c) 130 people d) 89 people
Answers
143 People
Given:
11 out of 100 like lizards
then
1300 out from ?
so
here increase of persons= 13
then
11 x 13 = 143
hence answers
Related Questions
I need to show you the picture to much to right down.
Answers
Answer:
The multiplication fraction that matches the model is;
\(\frac{1}{3}\times\frac{2}{5}=\frac{2}{15}\)Explanation:
Given the model shown in the attached image;
The model is divided into 3 columns, and the shaded part is only contained in one column, which gives;
\(\frac{1}{3}\)Also the model id divided into 5 rows, and only two rows of the 5 rows of the last column was shaded.
So, we have the multiplication fraction as;
\(\frac{1}{3}\times\frac{2}{5}=\frac{2}{15}\)Therefore, the multiplication fraction that matches the model is;
\(\frac{1}{3}\times\frac{2}{5}=\frac{2}{15}\)x + 3(2x - 5) = 4x – 12
Answers
Answer:
X is 9
X+6x-15=4x+12
3x-15=12
3x=27
x=9
SO x is 9
Answer:
x=9
Step-by-step explanation:
x + 3(2x - 5) = 4x – 12
distrubute left side
3 times 2x; 3 times -5
x+6x-15=4x-12
add like terms
x+6x
7x-15=4x-12
get all variables on the same side
7x-15=4x-12
-4x -4x
3x-15=12
add 15 to both sides
3x-15=12
+15 +15
3x=27
divide by 3 on both sides
3x/3=27/3
x=9
A 20 inch ribbon is cut into eighths, and 3 of the pieces are taped end-to-end. What is the total length. (I know how to answer it but I don’t know how to show my work)
Answers
Answer:
Step-by-step explanation:
Length of one piece = 20/8 inches = 2.5 inches.
3 pieces × (2.5 inches)/piece = 7.5 inches
To prove that a conjecture is true, you must show that it is true __________. for all possible situations most of the time in several examples. in just one example.
Answers
A valid proof requires showing that the conjecture holds true for all possible situations or providing evidence from multiple examples.
To prove that a conjecture is true, it is not sufficient to demonstrate its truth in just one example.
In mathematics, a conjecture is a statement that is believed to be true but has not been proven. To establish the validity of a conjecture, it is essential to provide evidence that supports its truth in all possible situations or through a rigorous proof.
Proving a conjecture true for all possible situations is a strong form of evidence. It means that the statement holds true regardless of any specific conditions or instances. By considering all possible cases, one can demonstrate the conjecture's validity across the entire domain of interest.
While a single example can provide some evidence and intuition towards the truth of a conjecture, it is not sufficient to establish its validity in general. A single example may be an exception or an instance that coincidentally satisfies the conjecture. Without further evidence or a systematic approach, relying on just one example can lead to incorrect conclusions.
To ensure the accuracy and reliability of a proof, mathematicians employ various techniques such as induction, contradiction, direct proof, and counterexamples. These methods allow for a comprehensive analysis of the conjecture's truth in multiple instances and generalizing the results to all possible situations.
In conclusion, proving a conjecture true requires demonstrating its validity in all possible situations or providing rigorous evidence from multiple examples. One example alone is insufficient as it does not account for all potential cases and may not represent the entire range of possibilities. A comprehensive and systematic approach is necessary to establish the truth of a conjecture.
Learn more about conjecture here:
brainly.com/question/29381242
#SPJ11
determine the expression -7c^3d is a polynomial or not. if it is a polynomial, state the type and degree of the polynomial
Answers
-7c^3d is a polynomial.
The expression can be written as - 7 c^3 dpolynomial is a combination of terms separated using + or − signs. Polynomials cannot contain any of the following:i)Variables raised to a negative or fractional exponent.i)Variables in the denominator.iii)Variables under a radical.iv)Special features. (trig functions, absolute values, logarithms, … ).-7c^3d is a polynomial.
3. College logo T-Shirts priced at $15 sell at a rate of 25t-shirts per week, but when the bookstore marks them down to $10, it finds that it can sell 50 t-shirts per week. What is the price elasticity of demand for the logo Tshirts? Is it elastic, inelastic or unit elastic and WHY? Did the t-shirt make a good decision in lowering the price of t-shirts? WHY OR WHY NOT? Explain by calculating total revenue for each price at $15 and $10 and then use the price-total revenue test format to see if t-shirts are elastic, inelastic or unit elastic and WHY.
Answers
The price elasticity of demand (PED) for the logo T-shirts is 1.67, indicating that the demand for T-shirts is elastic. Lowering the price from $15 to $10 increased the total revenue, suggesting that the T-shirt made a good decision in lowering the price. This is because the price change led to a significant increase in quantity demanded and overall revenue.
To calculate the price elasticity of demand (PED), we can use the following formula:
PED = ((Q2 - Q1) / ((Q2 + Q1) / 2)) / ((P2 - P1) / ((P2 + P1) / 2))
Given that Q1 = 25, Q2 = 50, P1 = $15, and P2 = $10, we can substitute these values into the formula:
PED = ((50 - 25) / ((50 + 25) / 2)) / (($10 - $15) / (($10 + $15) / 2))
Simplifying this expression:
PED = (25 / 37.5) / (-5 / 12.5)
PED = (-2/3) * (-2.5) = 1.67
The price elasticity of demand (PED) for the logo T-shirts is 1.67.
Since PED is greater than 1, it indicates that the demand for T-shirts is elastic. This means that a decrease in price by 1% will result in a greater than 1% increase in quantity demanded. To determine if lowering the price was a good decision, we can analyze the effect on total revenue. The price-total revenue test states that:
If PED is elastic (greater than 1), a decrease in price will lead to an increase in total revenue.
If PED is inelastic (less than 1), a decrease in price will lead to a decrease in total revenue.
If PED is unit elastic (equal to 1), a change in price will have no effect on total revenue.
Let's calculate the total revenue at both prices:
Total Revenue at $15 = $15 * 25 = $375
Total Revenue at $10 = $10 * 50 = $500
Comparing the total revenue at each price, we can see that lowering the price from $15 to $10 increased the total revenue from $375 to $500. Therefore, the T-shirt made a good decision in lowering the price because it led to an increase in total revenue.
To know more about price elasticity,
https://brainly.com/question/26309888
#SPJ11
plsss answer i'll give 50

Answers
Step-by-step explanation:
I know it not all but this is what I have

I will mark someone brainliest
The snack that smiles back ____
Answers
Answer:
goldfish
Step-by-step explanation:
Please help 30 extra points
Select only the rational numbers
3/4
6
0.863
1.5
103
Answers
Everything is rational
Answer:
the rational numbers are 6, 3/4, 1.5, 103, 0.863 so all of them.
Step-by-step explanation:
Any number that can be written, numbers like 2.3373648489 with no pattern or rationality are not rational.
However number like 2.3333 are rational because you can predict the pattern.
1) Determine the discriminant of the 2nd degree equation below:
3x 2 − 2x − 1 = 0
a = 3, b = −2, c = −1
Discriminant → ∆= b 2 − 4 a c
2) Solve the following 2nd degree equations using Bháskara's formula:
Δ = b² - 4.a.c
x = - b ± √Δ
__________
2a
a) x 2 + 5x + 6 = 0
b)x 2 + 2x + 1 = 0
c) x2 - x - 20 = 0
d) x2 - 3x -4 = 0
Answers
\( \LARGE{ \boxed{ \mathbb{ \color{purple}{SOLUTION:}}}}\)
We have, Discriminant formula for finding roots:
\( \large{ \boxed{ \rm{x = \frac{ - b \pm \: \sqrt{ {b}^{2} - 4ac} }{2a} }}}\)
Here,
x is the root of the equation.a is the coefficient of x^2b is the coefficient of xc is the constant term1) Given,
3x^2 - 2x - 1
Finding the discriminant,
➝ D = b^2 - 4ac
➝ D = (-2)^2 - 4 × 3 × (-1)
➝ D = 4 - (-12)
➝ D = 4 + 12
➝ D = 16
2) Solving by using Bhaskar formula,
❒ p(x) = x^2 + 5x + 6 = 0
\( \large{ \rm{ \longrightarrow \: x = \dfrac{ - 5\pm \sqrt{( - 5) {}^{2} - 4 \times 1 \times 6 }} {2 \times 1}}}\)
\(\large{ \rm{ \longrightarrow \: x = \dfrac{ - 5 \pm \sqrt{25 - 24} }{2 \times 1} }}\)
\( \large{ \rm{ \longrightarrow \: x = \dfrac{ - 5 \pm 1}{2} }}\)
So here,
\(\large{\boxed{ \rm{ \longrightarrow \: x = - 2 \: or - 3}}}\)
❒ p(x) = x^2 + 2x + 1 = 0
\(\large{ \rm{ \longrightarrow \: x = \dfrac{ - 2 \pm \sqrt{ {2}^{2} - 4 \times 1 \times 1} }{2 \times 1} }}\)
\(\large{ \rm{ \longrightarrow \: x = \dfrac{ - 2 \pm \sqrt{4 - 4} }{2} }}\)
\(\large{ \rm{ \longrightarrow \: x = \dfrac{ - 2 \pm 0}{2} }}\)
So here,
\(\large{\boxed{ \rm{ \longrightarrow \: x = - 1 \: or \: - 1}}}\)
❒ p(x) = x^2 - x - 20 = 0
\(\large{ \rm{ \longrightarrow \: x = \dfrac{ - ( - 1) \pm \sqrt{( - 1) {}^{2} - 4 \times 1 \times ( - 20) } }{2 \times 1} }}\)
\(\large{ \rm{ \longrightarrow \: x = \dfrac{ 1 \pm \sqrt{1 + 80} }{2} }}\)
\(\large{ \rm{ \longrightarrow \: x = \dfrac{1 \pm 9}{2} }}\)
So here,
\(\large{\boxed{ \rm{ \longrightarrow \: x = 5 \: or \: - 4}}}\)
❒ p(x) = x^2 - 3x - 4 = 0
\(\large{ \rm{ \longrightarrow \: x = \dfrac{ - ( - 3) \pm \sqrt{( - 3) {}^{2} - 4 \times 1 \times ( - 4) } }{2 \times 1} }}\)
\(\large{ \rm{ \longrightarrow \: x = \dfrac{3 \pm \sqrt{9 + 16} }{2 \times 1} }}\)
\(\large{ \rm{ \longrightarrow \: x = \dfrac{3 \pm 5}{2} }}\)
So here,
\(\large{\boxed{ \rm{ \longrightarrow \: x = 4 \: or \: - 1}}}\)
━━━━━━━━━━━━━━━━━━━━
Step-by-step explanation:
a)
given: a = 1, b = 5, c = 6
1) Discriminant → ∆= b² − (4*a*c)
∆= b² - (4*a*c)
∆= 5² - (4*1*6)
∆=25 - ( 24 )
∆= 25 - 24
∆= 1
2)
Solve x = (- b ± √Δ ) / 2a
x = ( 5 ± √25 ) / 2*1
x = ( 2 ± 5 ) / 2
x = ( 2 + 5 ) / 2 or x = ( 2 - 5 ) / 2
x = ( 7 ) / 2 or x = ( - 3 ) / 2
x = 3.5 or x = -1.5
b)
given: a = 1, b = 2, c = 1
1) Discriminant → ∆= b² − (4*a*c)
∆= b² - (4*a*c)
∆= 2² - (4*1*1)
∆= 4 - (4)
∆= 4 - 4
∆= 0
2)
Solve x = (- b ± √Δ ) / 2a
x = ( -2 ± √0) / 2*1
x = ( 2 ± 0 ) / 2
x = ( 2 + 0) / 2 or x = ( 2 - 0 ) / 2
x = ( 2 ) / 2 or x = ( 2 ) / 2
x = 1 or x = 1
x = 1 (only one solution)
c)
given: a = 1, b = -1, c = -20
1) Discriminant → ∆= b² − (4*a*c)
∆= b² - (4*a*c)
∆= -1² - (4*1*-20)
∆= 1 - ( -80 )
∆= 1 + 80
∆= 81
2)
Solve x = (- b ± √Δ ) / 2a
x = ( 2 ± √81 ) / 2*1
x = ( 2 ± 9 ) / 2
x = ( 2 + 9 ) / 2 or x = ( 2 - 9 ) / 2
x = ( 11 ) / 2 or x = ( - 7 ) / 2
x = 5.5 or x = -3.5
d)
given: a = 1, b = -3, c = -4
1) Discriminant → ∆= b² − (4*a*c)
∆= b² - (4*a*c)
∆= -3² - (4*1*-4)
∆= 9 - ( -16)
∆= 9 + 16
∆= 25
2)
Solve x = (- b ± √Δ ) / 2a
x = ( 3 ± √25 ) / 2*1
x = ( 3 ± 5 ) / 2
x = ( 3 + 5 ) / 2 or x = ( 3 - 5 ) / 2
x = ( 8 ) / 2 or x = ( - 2 ) / 2
x = 4 or x = -1
Use substitution to write an equivalent quadratic equation. (3x 2)2 7(3x 2) â€"" 8 = 0
Answers
Answer: We on da same question i do not know
Step-by-step explanation:
Please help as soon as possible

Answers
The domain of the given function g(x) = (x - 1)² is (−∞,∞), {x|x∈R} which is shown in the graph and is defined by the set of values x.
What are the domain and range of the function?The domain of the function includes all possible x values of a function, and the range includes all possible y values of the function.
We have been given the function below as
g(x) = (x - 1)²
We have to determine the domain of the given function.
The domain of the function shown in the graph is given by the set of values x that has a point on the graph.
As per the given graph, the range is the set of values that correspond with the domain.
Domain: (−∞,∞), {x|x∈R}
and the function shows that values of x are real numbers.
Thus, the required domain of the given function is (−∞,∞), {x|x∈R}
Learn more about the domain of the function here:
brainly.com/question/21027387
#SPJ1

HELLPPPP WILL GIVE BRAINLIEST

Answers
Answer:
\(\frac{-1+-\sqrt{41} }{4}\) (Third Option)
Step-by-step explanation:
Step 1: Use quadratic formula with a = 2, b = 1, c = -5.
\(x = \frac{-b+-\sqrt{b^2-4ac} }{2a}\) \(x = \frac{-(1)+-\sqrt{(1)^2-4(2)(-5)} }{2(2)}\) \(x = \frac{-1+-\sqrt{1-8(5)}}{4}\) \(x = \frac{-1+-\sqrt{1-40} }{4}\) \(x = \frac{-1+-\sqrt{41} }{4}\)Therefore, the answer is the third option, \(\frac{-1+-\sqrt{41} }{4}\).
Given circle C: x² + y² = 20, a straight line passes point P(6,4) and cuts the circle. The length of the chord cut by the line is 6√2. Find the equation of the straight line.
Answers
The equation of the straight line passing through point P(6,4) and cutting the circle x² + y² = 20 is y = 2x/3 - 4/3.
Let's denote the equation of the straight line as y = mx + c, where m represents the slope and c represents the y-intercept. We need to find the values of m and c that satisfy the given conditions.
Since the line passes through point P(6,4), we can substitute these coordinates into the equation:
4 = 6m + c ---(1)
The line also cuts the circle x² + y² = 20. The length of the chord cut by the line is given as 6√2. We know that the perpendicular distance between the line and the center of the circle is equal to the radius of the circle, which is √20 = 2√5. Using the formula for the distance between a point and a line, we have
|6m + c - 0| / √(m² + 1) = 2√5 ---(2)
Simplifying equation (2), we get:
(6m + c)² = 20(m² + 1)
36m² + 12mc + c² = 20m² + 20
16m² - 12mc + c² = 20
Substituting the value of c from equation (1) into equation (2), we get:
16m² - 12m(4 - 6m) + (4 - 6m)² = 20
Simplifying the equation above, we find:
12m² - 24m + 4 = 0
Solving this quadratic equation, we get two solutions: m = 1/2 and m = 1/3. Substituting these values back into equation (1), we can find the corresponding values of c:
For m = 1/2: c = -1
For m = 1/3: c = -4/3
Therefore, the equations of the straight line that passes through P(6,4) and cuts the circle are:
y = (1/2)x - 1 and y = (1/3)x - 4/3
Hence, the equation of the straight line is y = 2x/3 - 4/3.
Learn more about quadratic equation here: brainly.com/question/30098550
#SPJ11
ccording to the Texas Water Development Board, the average per capita per day water usage in this same area is 89 gallons. What are some reasons that the per capita per day water consumption be higher than the wastewater generated
Answers
There are several possible reasons why per capita per day water consumption could be higher than the wastewater generated:
Non-domestic water use: Per capita water usage includes not only water used in households but also water used for commercial, industrial, and agricultural purposes. Wastewater, on the other hand, only includes water that has been used in households and is discharged into the sewer system. Therefore, if there is significant non-domestic water use in the area, per capita water usage could be higher than wastewater generated.
Inefficient water use: Even though per capita water usage is high, some of the water used may not end up in the wastewater stream. For example, water may be used for landscaping or irrigation, and much of it could evaporate or soak into the ground before it reaches the sewer system. This would result in higher water usage than wastewater generated.
Water loss: The water distribution system may experience leaks or other losses, resulting in some of the water being lost before it reaches households or other water users. This would result in higher water usage than wastewater generated.
Infiltration and inflow: In some cases, rainwater or groundwater can infiltrate into the sewer system or inflow into wastewater treatment plants, increasing the volume of wastewater generated. This could result in lower wastewater generated than per capita water usage.
Time lag: There may be a time lag between water usage and wastewater generated, especially in areas with septic systems. It is possible that some of the water used today may not be discharged into the sewer system for several days or even weeks, resulting in higher per capita water usage than wastewater generated on any given day.
To learn more about wastewater here
https://brainly.com/question/30939874
#SPJ4
the length of a rectangle is 4 centimeters less than twice its width. find the dimensions if the area of the rectangle is 96 square centimeters.
Answers
The length=12cm and width=8cm of the rectangle.
What is area of rectangle?
The territory a rectangle occupies inside its four sides or limits is known as its area. A rectangle's sides determine its area. Basically, the area formula is equal to the rectangle's product of its length and width.
Here length = l ans width = w.
The length of rectangle is 4 cm less than twice its width.
=> l = 2w - 4
Then area of rectangle A= 96 sqaure centimeters.
=> A = l*w
=> 96 = (2w-4)w
=> 96= 2\(w^{2}\)-4w
=> 2\(w^{2}\)-4w = 96
=> 2\(w^{2}\)-4w-96=0
=> \(w^{2}\)-2w -48 =0
=> \(w^2\)-8w+6w-48=0
=> w(w-8)+6(w-8)=0
=> (w+6)(w-8)=0
=> w= -6,8
Then width w = 8 cm
Now l = 16-4 =12 cm.
Therefore the length = 12cm and width=8 cm.
To learn more about Area of rectangle
https://brainly.com/question/25292087
#SPJ4
a standard six-sided die is rolled. what is the probability of rolling a number equal to 1 ? express your answer as a simplified fraction or a decimal rounded to four decimal places.
Answers
Answer:
1/6 = 0.1667
Step-by-step explanation:
sample space = 6
the probability of rolling a number equal to 1 = 1/6
Consider the number pattern with general term Tn = 56 – 4n.
(i) Write the first three terms of this number pattern.
(ii) Show that 18 is not a term of this number pattern.
Answers
Answer:
for first three terms of this pattern
n=1,2,3
Tn= 52,48,44
Step-by-step explanation:
18 is not the term because let's say
18=56-4n
4n=56-18
4n= 38
n=9.5
but n should be a whole no. that's why 18 is not the term of this sequence
A line passes through the points (-2, 8) and
(5,-20). Which points lie on the same line?
Select all that apply.
(-6, -2)
(-3, 12)
(4, 16)
(0, 6)
(-1, 4)
(7,5)
Answers
The points that lies on the same line are (-3, 12), and, (-1, 4).
Here, we have,
The given coordinate points are (-2, 8) and (5,-20).
Here, slope (m)= 8+20/-2-5
= 28/-7
=-4
Substitute m= -4 and (x, y)=(-2,8) in y=mx+c, we get
8 = 8+c
or, c = 0
So, the equation of a line is y= -4 x
Now,
(-6, -2) in the given equation is -2=-4 (-6)
-2≠ 24
(-3, 12) in the given equation is y= -4 x
12 = 12
(4, 16) in the given equation is y= -4 x
16 ≠ -16
(0, 6) in the given equation is y= -4 x
6 ≠ 0
(-1, 4) in the given equation is y= -4 x
4 = 4
(7,5) in the given equation is y= -4 x
5 ≠ -28
Therefore, the points that lies on the same line are (-3, 12), and, (-1, 4).
To learn more about the equation of a line visit:
brainly.com/question/2564656.
#SPJ1
Can y’all help me ?

Answers
Answer:
-2 is 4
Step-by-step explanation:
Complete the statements to find the measurements of ∠a and ∠b

Answers
The measurements of <a is 105^o, and <b is 75^o.
What are supplementary angles?Two or more angles are said to be supplementary if their measures add up to 180^o.
In the given diagram, we have;
a. To find the measure of <a;
m<a + 40 + 35 = 180
m<a + 75 = 180
m<a = 180 - 75
= 105
m<a = 105^o
b. To find the measure of <b;
m<b + m<a = 180
m<b + 105 = 180
m<b = 180 - 105
= 75
m<b = 75^o
Learn more about supplementary angles at https://brainly.com/question/26760105
#SPJ1
Solve this question with full working and explanation and I will mark you as brainliest.

Answers
Answer:
The hand moved \(\bf \frac{3}{4}\) of a complete turn.
Step-by-step explanation:
The hand moved from 3 to 12, that is, it moved:
12 - 3 = 9 hours
In a clock, 12 hours represent a complete turn.
∴ Using the unitary method:
12 hours ⇒ 1 turn
1 hour ⇒ \(\frac{1}{12}\) turns
9 hours ⇒ \(\frac{1}{12}\) × 9 = \(\frac{9}{12}\)
= \(\bf \frac{3}{4}\) turns (simplified)
∴ The hand moved \(\bf \frac{3}{4}\) of a complete turn.
The answer is \(\boxed{\frac{3}{4}}\).
To find the fraction of a complete turn it moved in this case, take the ratio between hours covered between 3 and 12, and the hours covered in a complete turn.
Hours covered between 3 and 12 : 12 - 3 = 9Hours covered in a complete turn = 12Fraction of a complete turn it moved : 9/12 = 3/4- 5/6 * 1/8
Practice and problem solving
Answers
Answer:
- 6 and ?/6
Step-by-step explanation:
Just look at my pictute Haha. And btw it is negative because the fractions did not have the same sign as in one was positive and one was negative! Hope I helped! Please give me brainliest! Have a great day Adios. :)
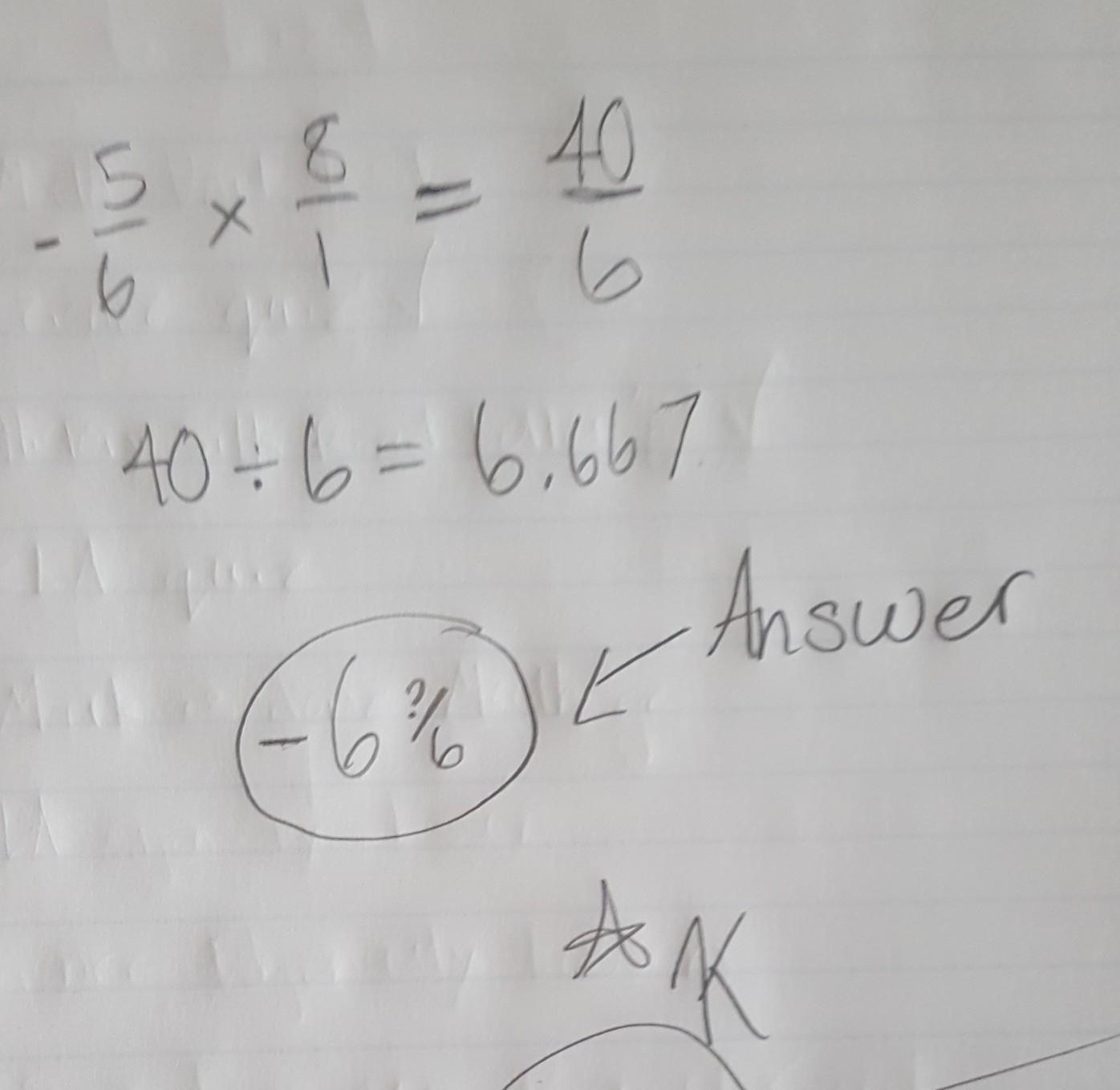
-5x+ 8y = 10
-4x+ y = -19
Answers
Answer:
(6, 5)
Step-by-step explanation:
find the volume of a pyramid with a square base, where the perimeter of the base is 5.7 cm 5.7 cm and the height of the pyramid is 8.6 cm 8.6 cm. round your answer to the nearest tenth of a cubic centimeter.
Answers
The volume of the pyramid is approximately 5.9 cm³.
What is the volume of pyramid?To find the volume of a pyramid with a square base, you can use the formula:
Volume = (1/3) * base area * height
First, let's find the area of the square base. The perimeter of the base is given as 5.7 cm, which means each side of the square has a length of 5.7 cm / 4 = 1.425 cm.
The area of a square is given by the formula:
Area = side length * side length
Substituting the side length, we have:
Area = 1.425 cm * 1.425 cm = 2.030625 cm²
Now, we can calculate the volume of the pyramid:
Volume = (1/3) * base area * height
= (1/3) * 2.030625 cm² * 8.6 cm
= 5.91834375 cm³
Rounding to the nearest tenth of a cubic centimeter, the volume of the pyramid is approximately 5.9 cm³.
Learn more about pyramid
brainly.com/question/13057463
#SPJ11
the ogive shown is based on u.s. census data and shows the average annual personal income per capita for each of the 50 states. the data are rounded to the nearest thousand dollars. ogive showing cumulative percentage of data webassign plot what percentage of the states have average per capita income more than 32.5 thousand dollars?
Answers
The estimated percentage of states with an average per capita income greater than 32.5 k is:we need to use the ogive (cumulative frequency curve) to determine the percentage of states with an average per capita income greater than 32.5k.
Assuming that the ogive is a continuous curve, we can estimate the percentage by finding the value on the horizontal axis corresponding to the 50% mark on the vertical axis, and then subtracting it from 100%. From the graph, we can see that the 50% mark corresponds to a value of around 30 k, which is between the values for Oklahoma and Pennsylvania. To get a more accurate estimate, we can use linear interpolation between these two data points.
Let's assume that the values for Oklahoma and Pennsylvania are
(x₁,y₁) = (25k,40%) and (x₂,y₂) = (35k,60%)
respectively. Then the equation of the straight line connecting these two points is:
(y-y₁) =(y₂-y₁) / (x₂-x₁) * (x-x₁)
Substituting in the values gives:
y - 40 = (0.6 - 0.4)/(35 - 25) * (x - 25)
y - 40 = 0.02(x - 25)
y = 0.02x - 0.5
To find the value of x that corresponds to the 50% mark, we can set y = 50% and solve for x:
50 = 0.02x - 0.5
0.02x = 50.5
x = 2525
So the estimated value for x is 25.25k. Therefore, the estimated percentage of states with an average per capita income greater than 32.5k is:
scss
Copy code
100% - 40% - (10% * (32.5 - 25.25)/(30 - 25))
= 50.5%
Therefore, we estimate that about 50.5% of the states have an average per capita income greater than 32.5k.
Find out more about ogive (cumulative frequency curve)
brainly.com/question/15902905
#SPJ4
Convert the rectangular equation to polar form
2x - y =3
Answers
Answer:
\(\dfrac{3}{2\cos\theta - r\sin\theta}\)
Step-by-step explanation:
The polar coordinate system uses two parameters r and θ where r is the magnitude of the radius of the circle in polar form(also known as the radial coordinate) and θ the angle which the which the radius makes relative to the x=axis
The following equations are used to convert from cartesian coordinate to polar coordinates
\(r = \sqrt{x^2 + y^2}\\\\\\x = r\cos\theta\\\\y= r\sin\theta\\\\\)
Substituting for x and y in terms of r and θ into the equation 2x - 3y = 3 gives
\(2x - y = 3\\\\2r\cos\theta - r\sin\theta = 3\\\\r(2\cos\theta - r\sin\theta = 3\\\\r = \dfrac{3}{2\cos\theta - r\sin\theta}\)
Give an example of an exponential function that includes the following transformations: o Vertical Compression o Reflection in the y-axis o Horizontal Stretch o Horizontal Translation to the left o Vertical Translation down
Answers
Step-by-step explanation:
A transformation may be defined as taking a basic function and then changing it slightly with the predetermined methods. This changes will cause the required graph of that function to shift, move or stretch, which depends on the type of the transformation.
For example:
Let a function be : \($f(x)= B^x$\)
For any constants m and n, the function \($f(x)= B^{x+m}+n$\) shifts the parent function.
- vertically n units and in same direction of the sign of n.
- horizontally m units and towards the opposite direction of the sign of m.
- The y-intercept becomes (\($0, b^m+n$\))
- The horizontal asymptote becomes y = n.
- the reflection about x -axis becomes \($f(x)=- B^x$\)
cos (2x) - cos(x) = 0
Answers
Answer:
x = 4πn/3 x = 2π/3 4πn/3
Step-by-step explanation:
Bob bought 40 gumboils from a quarter machine. The number of each flavor he got is shown in the table. If there are 140 gumboils remaining in the machine, what is a reasonable prediction for the number of cola flavored gumboils left?
Flavors: Amount:
Grape 4
Cherry 12
Cola 16
Orange 8
Answers
Answer:
56 cola flavored gumboils
Step-by-step explanation:
Bob's 40 count of gumballs has 16 cola gumballs
Therefore the probability of a gumball being cola based on the sample size of Bob's purchase = 16/40 = 2/5
There are 140 gumballs left in the machine so we can expect that, on an average, 2/5 of them should be cola gumballs
So number of cola gumballs left is expected to be 2/5 x 140 = 56
This is only a prediction based on Bob's sample of 40 cola gumballs