a varies jointly as the square root of the product of b and c. if a = 24 when b = 8 and c= 2 , find v when a = 48 and c = 4
Answers
Answer:
b = 16
Step-by-step explanation:
× stands for varies
a × √bc,
a = k√bc,
when a = 24, b = 8, c= 2
a = k√bc
24 = k√8•2
24 = k√16
24 = 4k
dividing both sides by 4
k = 24/4
k = 6
a = 6√bc (standard equation)
find b when a = 48 and c = 4
a = 6√bc
48 = 6√b•4
dividing both sides by 6
48/6 = √b•4
8 = √b•4
squaring both sides
8^2 = b•4
64 = b•4
b = 64/4
b= 16.
Thrrefore when a = 48, c = 4, b = 16.
Related Questions
Solve the following systems of equations using Gaussian Elimination. 2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Find the inner product of two vectors A = (2, -3,0) and B = = (-1,0,5)
Answers
The inner product of two vectors A = (2, -3,0) and B = (-1,0,5) is -2 / √(13×26).
Solving the given system of equations using Gaussian elimination:
2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Matrix form of the system is
[A] = [B] 2 3 1 | 2 0 5 | 20 -1 2 3 | 13
Divide row 1 by 2 and replace row 1 by the new row 1: 1 3/2 1/2 | 1
Divide row 2 by 5 and replace row 2 by the new row 2: 0 1 1 | 4
Divide row 3 by -1 and replace row 3 by the new row 3: 0 0 1 | 5
Back substitution, replace z = 5 into second equation to solve for y, y + 5(5) = 20 y = -5
Back substitution, replace z = 5 and y = -5 into the first equation to solve for x, 2x + 3(-5) + 5 = 2 2x - 15 + 5 = 2 2x = 12 x = 6
The solution is (x,y,z) = (6,-5,5)
Therefore, the solution to the given system of equations using Gaussian elimination is (x,y,z) = (6,-5,5).
The given two vectors are A = (2, -3,0) and B = = (-1,0,5). The inner product of two vectors A and B is given by
A·B = |A||B|cosθ
Given,A = (2, -3,0) and B = (-1,0,5)
Magnitude of A is |A| = √(2²+(-3)²+0²) = √13
Magnitude of B is |B| = √((-1)²+0²+5²) = √26
Dot product of A and B is A·B = 2(-1) + (-3)(0) + 0(5) = -2
Cosine of the angle between A and B is
cosθ = A·B / (|A||B|)
cosθ = -2 / (√13×√26)
cosθ = -2 / √(13×26)
Learn more about equation at
https://brainly.com/question/12998758
#SPJ11
In Raphael"s class there are 14 boys and 10 girls select whether each statment is true or false
\
Answers
Answer:
I can't see the statement
Step-by-step explanation:
Find the Volume of the Prism.
Height= 3cm
Length=8cm
Width=5cm
Please help

Answers
Step-by-step explanation:
To find the volume of a rectangular prism, multiply its 3 dimensions: length x width x height. The volume is expressed in cubic units.
Marc is filling 1-cup containers with juice.
He has 5 gallons of juice. How many 1-cup
containers can he fill? (1 gallon = 16 cups)
Answers
Answer:
80
Step-by-step explanation:
5*16 = 80
Hence, the Marc has the number of cups are \(80\).
What is the equation?
An equation can be defined as a mathematical statement consisting of an equal symbol between two algebraic expressions that have the same value.
The most basic and common algebraic equations in math consist of one or more variables.
Here given that,
Marc is filling one-cup containers with juice. He has five gallons of juice.
As we know,
\(1gallon=16cups\)
So, it would be \(5(16)=80\).
Hence, the Marc has the number of cups are \(80\).
To know more about the equation
https://brainly.com/question/12788590
#SPJ2
Directions: Find the specified term of the geometric sequences given the first term and the common ratio.

Answers
Step-by-step explanation:
As you know
\( a_{n} = a_{1} \times {r}^{n - 1} \)
1.
\(3 \times {3}^{4} = {3}^{5} \\ 3 \times {3}^{6} = {3}^{7} \\ 3 \times {3}^{8} = {3}^{9}\)
2.
\(2 \times {2}^{4} = {2}^{5} \\ 2 \times {2}^{6} = {2}^{7} \\ 2 \times {2}^{8} = {2}^{9}\)
3.
\( - \frac{1}{2} \times {( - 6)}^{4} = { \frac{ - 1}{2} } \times {6}^{4} \\ - \frac{1}{2} \times {( - 6)}^{6} = { \frac{ - 1}{2} } \times {6}^{6} \\ - \frac{ 1}{2} \times {( - 6)}^{8} = { \frac{ - 1}{2} } \times {6}^{8} \)
A family has two children. What is the probability that both the children are boys given that at least one of them is a boy?
Answers
Answer:
the probability is 1/2
Step-by-step explanation:
the probability of a child being a boy is 1/2, if at least one of them is already a boy, then the probability of both being boys, which amounts to saying that the other is also a boy, is 1/2
y−5=23(x+4) what is the slope of this equation please
Answers
Answer:
The slope of the equation is 23
Step-by-step explanation:
First, we must simplify/solve the equation in order to find the slope
Let's get rid of the parentheses
y - 5 = 23x + 92
Then, combine like terms by moving 5 to the right side of the equation
y - 5 + 5 = 23x + 92 + 5
y = 23x + 97
The slope is always the number that is paired with "x"
need help with math problem if do 5 star
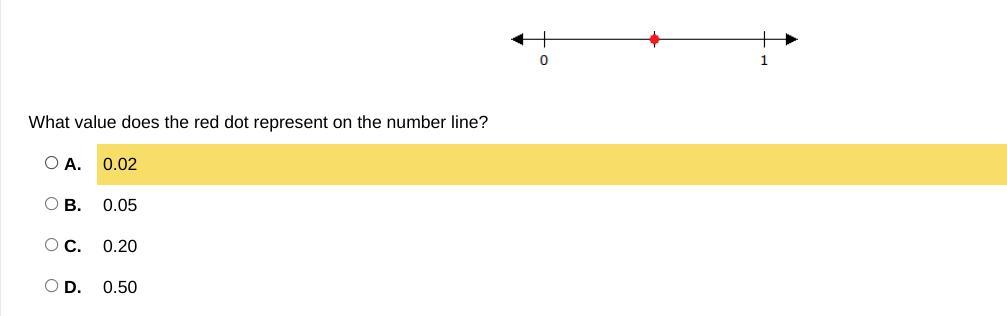
Answers
Answer:
D.
Step-by-step explanation:
the dot is right in between zero and one, which makes it 0.50
Answer:
D. 0.50
Between 0 and 1 is 0.50 or 0.5 or \(\frac{1}{2}\)
1.Find the period of the following functions. a) f(t) = (7 cos t)² b) f(t) = cos (2φt²/m)
Answers
Period of the functions: The period of the function f(t) = (7 cos t)² is given by 2π/b where b is the period of cos t.The period of the function f(t) = cos (2φt²/m) is given by T = √(4πm/φ). The period of the function f(t) = (7 cos t)² is given by 2π/b where b is the period of cos t.
We know that cos (t) is periodic and has a period of 2π.∴ b = 2π∴ The period of the function f(t) =
(7 cos t)² = 2π/b = 2π/2π = 1.
The period of the function f(t) = cos (2φt²/m) is given by T = √(4πm/φ) Hence, the period of the function f(t) =
cos (2φt²/m) is √(4πm/φ).
The function f(t) = (7 cos t)² is a trigonometric function and it is periodic. The period of the function is given by 2π/b where b is the period of cos t. As cos (t) is periodic and has a period of 2π, the period of the function f(t) = (7 cos t)² is 2π/2π = 1. Hence, the period of the function f(t) = (7 cos t)² is 1.The function f(t) = cos (2φt²/m) is also a trigonometric function and is periodic. The period of this function is given by T = √(4πm/φ). Therefore, the period of the function f(t) = cos (2φt²/m) is √(4πm/φ).
The period of the function f(t) = (7 cos t)² is 1, and the period of the function f(t) = cos (2φt²/m) is √(4πm/φ).
To learn more about trigonometric function visit:
brainly.com/question/25618616
#SPJ11
Suppose that a linear system of equations in unknowns x, y, and z has the following augmented matrix.
Use Gauss-Jordan elimination to solve the system for x, y, and z.
Answers
Given a linear system of equations in unknowns x, y, and z with the following augmented matrix:{[1, -1, 0, 0, -7], [-2, 3, 0, 0, 2], [0, 0, 4, -2, 2]}Use Gauss-Jordan elimination to solve the system for x, y, and z.Solution:Step 1. The first step in solving this linear system of equations is to write the matrix in the form of an augmented matrix. In the following, we list the system of equations associated with the augmented matrix: 1x−1y=−72x+3y=24z−y=1 We begin by focusing on the first equation, which is:1x−1y=−7.
To get rid of the x-coefficient, we add one time the first equation to the second equation. This operation is written as follows:{[1, -1, 0, 0, -7], [-2, 3, 0, 0, 2], [0, 0, 4, -2, 2]}We add row1 to row2. -2r1 + r2 = r2{-2, 2, 0, 0, 14}r3 = r3This gives us the new augmented matrix.{[1, -1, 0, 0, -7], [0, 1, 0, 0, -5], [0, 0, 4, -2, 2]}Step 2Next, we focus on the second equation:0x+1y=−5.
The y-variable is isolated, and we now look at the third equation.4z−2y=1We can isolate the variable z by dividing the entire equation by 4 as follows:z−0.5y=0.25In order to eliminate y in the third row, we add 0.5 times the second row to the third row. This operation is written as follows:{[1, -1, 0, 0, -7], [0, 1, 0, 0, -5], [0, 0, 4, -2, 2]}We add 0.5 r2 to r3. r3 + 0.5r2 = r3{[1, -1, 0, 0, -7], [0, 1, 0, 0, -5], [0, 0, 4, -1, -1]}Step 3We can now solve for z using the third equation:4z−1y=−1z = (-1 + y) / 4.
Substituting this into the second equation gives:-2((1 - y) / 4) + 3y = 2y - 1 = 2y - 1Thus, y = 1/2.Substituting the value of y = 1/2 into the first equation gives:x - (1/2) = -7, so x = -13/2.Finally, we can substitute the values of x and y into the third equation to get the value of z: 4z - 1(1/2) = -1, so z = -3/2.The solution to the system of linear equations is: x = -13/2, y = 1/2, and z = -3/2.
Learn more about linear system of equations:
https://brainly.com/question/13729904
#SPJ11
a culture initially has 6,000 bacteria, and its size increases by 3% every hour. how many bacteria are present at the end of 6 hours? (round your answer to the nearest whole number.)
Answers
The number of bacteria present at the end of 6 hours is approximately 8,247.
To solve this problem, we need to use the formula for exponential growth, which is: N = N0 * e^(rt) where N is the final number of bacteria, N0 is the initial number of bacteria, r is the growth rate (in this case, 0.03), t is the time (in hours).
Using the given values, we can plug them into the formula: N = 6,000 * e^(0.03*6) Simplifying this expression, we get: N ≈ 8,247 Therefore, at the end of 6 hours, there will be approximately 8,247 bacteria in the culture.
Learn more about exponential growth here:
https://brainly.com/question/29160729
#SPJ11
State whether the indicated angles are Complementary, Supplementary, adjacent, vertical, or form a linear Pair.

Answers
Answer:
Attached is the image to help you find the answer.

PLease help, (last Mistake) -_-

Answers
Answer:
B.61kg
Step-by-step explanation:
use the formula
force÷acceleration=mass
183÷3=61kg
If output grows by 21.6% over 7 years, what is the annualized (or annual) growth rate? Write the answer in percent terms with up to two decimals (e.g., 10.22 for 10.22%, or 2.33 for 2.33%)
Answers
The annual growth rate is 23.81%
The annual growth rate is the percentage increase of the production or an investment over a year. It's the annualized growth rate of the output.The formula for the annual growth rate is given as:
Annual Growth Rate = (1 + r)^(1 / n) - 1
Where,‘r’ is the growth rate, and‘n’ is the number of periods considered.
The percentage increase in the output over seven years is given as 21.6%.
The annual growth rate can be calculated as:
(1 + r)^(1 / n) - 1 = 21.6 / 7Or (1 + r)^(1 / 7) - 1 = 0.031
Therefore, (1 + r)^(1 / 7) = 1 + 0.031r = [(1 + 0.031)^(7)] - 1 = 0.2381
The annual growth rate is 23.81% (approx) in percent terms.
Therefore, the answer is "The annualized growth rate is 23.81%."
Know more about growth rate here,
https://brainly.com/question/13870574
#SPJ11
PLS HELP ME ASAP!
The amount of money in an account may increase due to rising stock prices and decrease due to falling stock prices. Maggie is studying the change in the amount of money in two accounts, A and B, over time.
The amount f(x), in dollars, in account A after x years is represented by the function below:
f(x) = 9,628(0.92)x
Part A: Is the amount of money in account A increasing or decreasing and by what percentage per year? Justify your answer. (5 points)
Part B: The table below shows the amount g(r), in dollars, of money in account B after r years.
r (number of years) 1 2 3 4
g(r) (amount in dollars) 8,972 8,074.80 7,267.32 6,540.59
Which account recorded a greater percentage change in amount of money over the previous year? Justify your answer. (5 points)
(10 points)
Answers
Account A: Decreasing at 8 % per year
Account B: Decreasing at 10.00 % per year
Account B shows the greater percentage change
What is Exponential Function?Exponential function, in mathematics, a relation of the form y = \(a^x\), with the independent variable x ranging over the entire real number line as the exponent of a positive number a.
Given:
f(x) = 9628(0.92)ˣ
A)The general formula for an exponential function is
y = a\(b^x\), where b = the base of the exponential function.
if b < 1, we have an exponential decay function.
So, ƒ(x) decreases as x increases.
Thus, Account A is decreasing each year.
B) Now, the formula for an exponential decay function as:
y = a(1 – b)ˣ, where
1 – b = the decay factor
If we compare the two formulas, we find
0.92 = 1 - b
b = 1 - 0.92 = 0.08
b = 8 %
The account is decreasing at an annual rate of 8 %.
The account is decreasing at an annual rate of 10.00 %.
Account B recorded a greater percentage change in the amount of money over the previous year.
Learn more about Exponential Function here:
https://brainly.com/question/14355665
#SPJ1
use the Pythagorean theorem to find L

Answers
Answer:
l = Square root of 10
Help!!! Carla earns $6.25 per hour working at a store. When she gets her paycheck she repays her brother $40. She has at least $120 left over. Rounding to the nearest hour, which is the minimum number of hours Carla worked?
Answers
Each marble bag sold by Chau's Marble Company contains 2 red marbles for every 3 blue marbles. If a bag has 18blue marbles, how many red marbles does it contain?
Answers
Answer:
12 red marbles.
Step-by-step explanation:
No step by step explanation.
Collen and Maureen get paid per project. Collen is paid a project fee of $44 plus $12 per hour. Maureen is paid a project fee of $35 plus $15 per hour. Write an expression to represent how much a company will pay to hire both to work the same number of hours on a project.
Let h represent the number of hours.
Answers
Answer:
Collen: 12h+44
Maureen: 15h+35
Step-by-step explanation:
For Collen, 44 dollars is the initial pay per project, then $12 every hour
For Maureen, 35 dollars is the initial pay per project, then $15 every hour
Hope this helps! If you found my answer helpful, please consider marking me brainliest. Thank you!
Answer:
79 +27h
Step-by-step explanation:
If both contractors are hired, the company will pay the sum of their costs.
cost for Collen: 44 +12h
cost for Maureen: 35 +15h
cost for both: (44 +12h) +(35 +15h) = 79 +27h
Hi again so this problem I got stuck on can someone help me with this thank u so much and also I hope everyone had a good thanksgiving ❤️

Answers
Step by step:
A:
2x+8=-3.5x+19
2x+3.5x=19-8
5.5x=11
x=2
B:
9(x-2)=7x+5
9x-18=7x+5
9x-7x=5+18
2x=23
x=11.5
C:
3(3x+2)-2x=7x+6
9x+6-2x=7x+6
7x+6=7x+6
No solution
4 minus (2X -3) = 3 what is x
Answers
Given the following equation:
\(4-(2x-3)=3\)You can solve for "x" by following these steps:
1. You must distribute the negative sign of the left side of the equation:
\(4-2x+3=3\)2. Now you need to add the like terms of the left side of the equation:
\(7-2x=3\)3. Apply the Subtraction property of equality by subtracting 7 from both sides of the equation:
\(\begin{gathered} 7-2x-(7)=3-(7) \\ -2x=-4 \end{gathered}\)4. Finally, you can apply the Division property of equality by dividing both sides of the equation by -2:
\(\begin{gathered} \frac{-2x}{-2}=\frac{-4}{-2} \\ \\ x=2 \end{gathered}\)The answer is:
\(x=2\)The points (2,3) and (6,11) lie on a line.What is the slope of the line?
Answers
Answer: the slope is 2!
Step-by-step explanation:
Answer:
slope: 2
Step-by-step explanation:
use this formula: 11- 3/6-2 = 2

I need help fast I’m trying to get all my work in for school today

Answers
Answer:
\(b+3+60\) → \(No\)
\(-30-24z\) → \(No\)
\(27n+66p\) → \(Yes\)
\(36-9j+3k\) → \(Yes\)
\(---------\)
hope it helps...
have a great day!!
Penny walked 50 yards in 30 seconds. At this pace, how many miles would she walk
in one hour? Show all calculations to get full credit.
CONVERSIONS:
1 yard = 3 feet
5,280 feet = 1 mile
1 hour = 60 minutes
1 minute = 60 seconds
Answers
50 yards x 200 = 10,000
10,000 divided by 3 = 3,333.3 feet
3,333.3 feet divided by 5,280 = 0.63 mile
Estimation: Penney will walk one mile and a quarter of another mile in one hour.
From a well shuffled deck of 52 playing cards, all diamond cards are removed. Now, a card is drawn from the remaining pack at random. Find the probability that the selected card is a king.
Answers
King , queen and jack of diamond are removed from a deck of 52 cards Remaning=52−3=49
1. Total card of diamond =13
King , queen and jack in removed
Then card =13−3=10
P(E)=P(Diamondcard
49
10
2. P(Jack)=
Totalcard
TotalJackinDeck
=
49
3
lost-time accidents occur in a company at a mean rate of 0.5 per day. what is the probability that the number of lost-time accidents occurring over a period of 8 days will be no more than 2? round your answer to four decimal places.
Answers
The required the probability that accidents occur no more than 2 days in 8 days is 0.144.
What is Probability?Probability is tied in with assessing or computing how likely or 'plausible' something is to occur. The opportunity of an occasion happening can be depicted in words, for instance 'certain', 'unimaginable' or 'logical'. In math, probabilities are constantly composed as portions , decimals or rates with values somewhere in the range of 0 and 1.
According to question:We have,
Probability(p) of lost-time accidents occur in a company at a mean rate of 0.5 per day.
Then, the Probability(q) of accident is not occur is 1 - 0.5 = 0.5.
The likelihood that a mishap doesn't happen (q) is then determined utilizing the accompanying supplement rule.
p =0.5 , q = 0.5
Each probability is calculated using:
P = ⁿCₐpᵃqⁿ⁻ᵃ
The probability that accidents occur no more than 2 days in 8 days is
P(x≤2) = P(0) + P(1) + P(2)
P(x≤2) = ⁸C₀p₀p⁰q⁸⁻⁰ + ⁸C₁p¹q⁸⁻¹ + ⁸C₂p²q⁸⁻²
P(x≤2) = (0.5)^8 + 8(0.5)(0.5)^7 + 28(0.5)^2(0.5)^6
P(x≤2) = 37(0.5)^8
P(x≤2) = 37(0.00390625) = 0.144
Hence, the probability that accidents occur no more than 2 days in 8 days is 0.144.
To know more about Probability visit:
brainly.com/question/15124899
#SPJ4
HELP ME!!!!!!!!!!! ANSWER 6-10





Answers
Answer:
LOOK BELOW!
Step-by-step explanation:
6#
6. (-3, 0)
7. (-1, -2)
8. (-5, -3)
9. (1, -1)
10. (1, -2)
how did I get these answers? I used a app called math - way, you can take a photo of the problem youre tryna do an it solves it, yw! :)
\(\huge\underline\mathbb\purple{ANSWER\::}\\\\\)
6. (-3,0)
7. (-1,-2)
8. (-5,-3)
9. (1,-1)
10. (1,-2)
\(\\\\\\\)
HOPE IT HELPS
PLEASE MARK ME BRAINLIEST ☺️
Which is the approximate measure of angle yzx? 34.8° 39.4° 50.6° 55.2°
Answers
The approximate measure of angle YZX is 39.4°. Option(B) is the correct answer.
we know that
In the right triangle XYZ
\(tan(Y Z X)= \frac{opposite side angle YZX}{adjacent side angle YZX}\)
In this problem,
Opposite side angle YZX= XY = 12.4cm
Adjacent side angle YZX= YZ = 15.1cm
substitute the values,
\(tan ( Y Z X) = \frac{12.4}{15.1}\)
\(Angle ( Y Z X) = arc tan( \frac{12.4}{15.1} )\)
Angle ( Y Z X) = 39.4°
So, the approximate measure of angle YZX is 39.4°.
Read more about the right triangle:
https://brainly.com/question/2437195
#SPJ4
The complete question is:
In right triangle XYZ, the right angle is located at vertex Y. The length of line segment XY is 12.4 cm. The length of line segment YZ is 15.1 cm. Which is the approximate measure of angle YZX?
A .34.8°
B .39.4°
C .50.6°
D. 55.2°
consider the expression\[x^2 18x \boxed{\phantom{00}}.\] find all possible values for the missing number that make this expression the square of a binomial.
Answers
The missing number is 81.
Consider the expression\[x^2 18x \boxed{\phantom{00}}.\]
We have to find all the possible values of the missing number that makes this expression a square of a binomial. To find the value of the missing number we have to divide the coefficient of the x term by 2 and then square it. The value that we obtain will be the value of the missing term.
So, the coefficient of x is 18.
Let's use the formula now:\[\text{Missing term }= \left( {\frac{{18}}{2}} \right)^2 = 9^2 = 81\]
Therefore, the missing number is 81.
Learn more about binomial here:
https://brainly.com/question/30339327
#SPJ11
Select the correct answer. Let f(x) and g(x) be polynomials as shown below. Which of the following is true about f(x) and g(x)? f(x) and g(x) are closed under multiplication because when multiplied, the result will be a polynomial. f(x) and g(x) are closed under multiplication because when multiplied, the result will not be a polynomial. f(x) and g(x) are not closed under multiplication because when multiplied, the result will be a polynomial. f(x) and g(x) are not closed under multiplication because when multiplied, the result will not be a polynomial.
Answers
f(x) and g(x) are not closed under subtraction because when subtracted, the result will be a polynomial, the correct option is B.
What is Polynomial?A polynomial is a mathematical equation that solely uses the operations addition, subtraction, multiplication, and non-negative integer exponentiation of variables. Variables are sometimes known as indeterminate in mathematics. Majorly used polynomials are binomial and trinomial.
Given f(x) and g(x) two polynomial functions in the standard form of the polynomial,
According to Closure Property, when something is closed, the output will be the same as the input.
The polynomials f(x) and g(x) can be seen in the image.
On subtracting the two polynomials, the output will be a polynomial and so it is closed under subtraction.
Therefore, The reason why f(x) and g(x) are not closed under subtraction is that the outcome of subtraction will be a polynomial, making option B the best choice.
Learn more about Polynomials here:
https://brainly.com/question/11536910
#SPJ1
Complete question:
