ABCDE is a convex pentagon. Given AB = 5, BC = 12, AE = 13, DE = 8, CD = 6, and m∠B=m∠D=90°. Find the area of ABCDE.
Answers
The diagonals AC and EC of the pentagon forms two right
triangles and on isosceles triangle, together which gives the
area of the pentagon.
Correct response:
The area of the convex pentagon is 104 square units.Which is the methods used to finding the area of a pentagonThe area of the convex polygon is found by the sum of the
areas of the three triangles that are formed by drawing two
diagonals facing the two 90° angles.
The given parameters are;
AB = 5
BC = 12
AE = 13
DE = 8
CD = 6
m∠B = m∠D = 90°
Required:
The area of the convex pentagon ABCDE
Solution:
The area of pentagon ABCDE = Right ΔABC + Right ΔCDE + ΔACE
Area of right triangle ΔABC = \(\frac{1}{2}\) × 5 × 12 = 30
Area of right triangle ΔCDE = \(\frac{1}{2}\) × 6 × 8 = 24
Length of AC = \(\mathbf{\sqrt{\overline{AB}^2 + \overline{BC}^2}}\)
Which gives; AC = \(\mathbf{\sqrt{5^2 + 12^2}}\) = 13
Length of EC = \(\mathbf{\sqrt{\overline{CD}^2+ \overline{DE}^2}}\)
Which gives; EC = \(\mathbf{\sqrt{6^2 + 8^2}}\) = 10
Therefore, ΔACE is an isosceles triangle
Base of ΔACE = EC
Therefore;
Height of isosceles triangle ΔACE = \(\mathbf{\sqrt{13^2 - 5^2}}\) = 12
Area of ΔACE = \(\mathbf{\frac{1}{2}}\) × 10 × 12 = 60
Therefore;
Area of the convex pentagon ABCDE = 30 + 24 + 60 = 104Learn more about finding the area of geometric figures here:
https://brainly.com/question/2279661
Related Questions
the length of the segment between the points $(2a, a-4)$ and $(4, -1)$ is $2\sqrt{10}$ units. what is the product of all possible values for $a$?
Answers
To find the length of the segment between the given points, we can use the distance formula. The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
\[d = \sqrt{{(x_2 - x_1)^2 + (y_2 - y_1)^2}}\]
Let's apply this formula to the given points: $(2a, a-4)$ and $(4, -1)$.
The distance between these two points is $2\sqrt{10}$ units. So we have:
\[2\sqrt{10} = \sqrt{{(4 - 2a)^2 + (-1 - (a-4))^2}}\]
Simplifying the equation, we get:
\[4\sqrt{10} = \sqrt{{(4 - 2a)^2 + (-5 - a)^2}}\]
Squaring both sides of the equation, we have:
\[160 = (4 - 2a)^2 + (-5 - a)^2\]
Expanding the equation, we get:
\[160 = 16 - 16a + 4a^2 + 25 + 10a + a^2\]
Combining like terms, we have:
\[0 = 5a^2 - 6a + 1\]
Now, we can solve this quadratic equation for the possible values of $a$.
Factoring the equation, we have:
\[0 = (5a - 1)(a - 1)\]
Setting each factor equal to zero and solving for $a$, we get:
\[5a - 1 = 0 \quad \Rightarrow \quad a = \frac{1}{5}\]
\[a - 1 = 0 \quad \Rightarrow \quad a = 1\]
Therefore, the possible values for $a$ are $\frac{1}{5}$ and $1$. The product of these values is:
\[\left(\frac{1}{5}\right) \cdot 1 = \frac{1}{5}\]
So, the product of all possible values for $a$ is $\frac{1}{5}$.
Learn more about distance formula here : brainly.com/question/25841655
#SPJ11
The sum of the relative frequencies for all classes will always equal
a. the sample size
b. the number of classes
c. one
d. 100
Answers
The sum of the relative frequencies for all classes will always equal (c) one
How to complete the statement?To start with, the relative frequency of a class is the frequency of the class divided by the total frequency of the of all classes
Mathematically, this is represented as
Relative frequency of class A = Frequency of class A/Total frequency of all classes
When the relative frequencies are summed up, they will always equal to 1
This is so because they have a part-whole ratio
Hence, the correct option is (c) one
Read more about relative frequency at
https://brainly.com/question/16148316
#SPJ1
Which choices are equivalent to the fraction below

Answers
Answer:
E and F
Step-by-step explanation:
(16/20 = 0.80)
14/8 = 1.75
9/10 = 0.90
8/5 =1.60
13/10 = 1.30
4/5 = 0.80
8/10 = 0.80
You have to to put the reduce the fractions and then put them in to decimal form then see if they are the same as the one you want it to be.
Which of the following best describes ethics?
it is a set of thoughts that are made about kinds of individuals
or their manners of conducting activities
it is a set of values that define r
Answers
Answer:
the second
Step-by-step explanation:
refers to well-founded standards of right and wrong that prescribe what humans should do, usually in terms of rights, obligations, benefits to society, justice
The inverse of the function f(x) = 1/2x + 10is shown.
h(x) = 2x-0
What is the missing value?
Answers
Answer:
20
Step-by-step explanation:
the inverse of
y=1/2x + 10
is
x=1/2y+10
from here you just solve for y
x-10 = 1/2y
2(x-10) = y
2x-20 = y
WILL MARK BRAINLIEST HELP ASAP ASAP

Answers
Answer:
B
Step-by-step explanation:
I got this answer correct on a test
Sally saved 65% of her pay check. If she made $500, how much did she save?
Answers
Answer: 325 dollars
Step-by-step explanation:
In order to find out a percentage of somethin, you can simply multiply and divide
\(500*65=32500\)
32500÷100= 325
Multiply 5c(9 − 4c).

Answers
Answer:
45c−20c2
Step-by-step explanation:
have great day
helpppppp fjekdjdjdj

Answers
Answer:
GIVE BRAINLEST PLZ :)
a) 3
b) 24
Step-by-step explanation:
Two right angle triangles that share two lines have a common angle.
Because of this the ratio of dimensions will remain the same, since this inner angle cannot change
This means we can look at the ratio of the lengths (questions calls it widths)
convention is to go from big to small. The easiest way is to use the large side and divide by the small
RATIO : =
With this ratio we can convert a small dimension into the relative big one.
W = w * R = 8 * 3 = 24m
EXTRA: Easyier way is to just realize the ratio of both dims must be equal
\(\frac{w}{l} = \frac{W}{L} => \frac{8}{10} = \frac{W}{30}\\Rearrange and solve :)\)
working with a manufacturing process which produces compsites having a fiber volume fraction a (msi) and a matrix with a matrix modulus b (msi). determine the fiber modulus required to produce a composite with longitudinal modulus of c (msi).
Answers
The fiber modulus required to produce a composite with longitudinal modulus of c is 56.93.
What is manufacturing process?
Manufacturing process management is a group of tools and techniques that specify how goods should be produced. MPM is distinct from ERP/MRP, which is used to schedule manufacturing, gather cost information, and organize the ordering of supplies and other resources.
What is matrix?
A matrix, which is used to represent a mathematical object or an attribute of one, is a rectangular array or table containing numbers, symbols, or expressions that are organized in rows and columns. is a matrix having two rows and three columns, for instance.
As a result, if we look at the formula for the relationship between the fiber modulus and the matrix's volume fraction, composite modulus, and fiber vol fraction, we have:
C = (M x B) / [(1-A)M + A x B]
where M denotes the fiber's modulus.
If you provide the corresponding letter values,
40 = M X 0.5 / [(1-0.7)M + 0.7 X 0.5]
M = 56.93
Hence,the fiber modulus required to produce a composite with longitudinal modulus of c (msi) is 56.93
Learn more about fiber modulus click here:
https://brainly.com/question/15060560
#SPJ4
Which equation represents the horizontal line passing through (-1,2)?
A. x = -1
B. y = -1
C. x = 2
D. y = 2
Answers
D. y = 2
Find the coordinates of point I so Δ I K L is the indicated type of triangle. Point J has coordinates (0,0) and point K has coordinates (2 a, 2 b) .
isosceles triangle
Answers
The coordinate of the point L is such that ΔL K L is an isosceles triangle that will be either (0,y) or (2a,y).
It is given that in ΔL K L , J has coordinates (0,0) and K has coordinates (2 a, 2 b) .
We have to find the coordinates of point L so that , ΔL K L is an isosceles triangle.
What is a triangle ?
A triangle is a 3-sided shape. There are three sides and three angles in every triangle, some of which may be the same.
As per the question ;
The ΔL K L is an isosceles triangle,
J has coordinates (0,0)
K has coordinates (2 a, 2 b) .
The possible coordinate of the point L will be (0,y) or (2a,y).
Let's check it.
Using the distance formula ;
JK = \(\sqrt{(2a-0)^2 + (2b -0)^2}\)
JK = \(\sqrt{(4a^2 + 4b^2)}\)
JK = \(2\sqrt{a^2 + b^2}\)
Similarly ;
JL = \(\sqrt{0^2 + y^2}\)
JL = y
And
KL = \(\sqrt{4a^2 + (2b - y)^2}\)
Let's say two sides JK and KL are equal at any value of a , b and y.
Then ;
The two sides are of equal length , so , we can conclude that this is an isosceles triangle.
Thus , the coordinate of the point L is such that ΔL K L is an isosceles triangle that will be either (0,y) or (2a,y).
To learn more about triangles click here ;
https://brainly.com/question/2773823
#SPJ4
4. When solving an equation, Henry gets to
the last line of his work and is left with "2 = 3".
What does this mean?
A. The solution is 3.
B. There is only one solution.
C. There is no solution.
D. There are infinite solutions.
1pt
Answers
3n + 19 = 28
How do I solve this
Answers
Answer:
to solve this you need to find out what number n is to make it equal 28.
Step-by-step explanation:
19+3 =22 so 3 is not it
19+9=28
answer is 9
hopefully this is right and this gets to you on time
Answer:
err Im not sure if this is a multiple-choice but n=3
Step-by-step explanation:
3(n) + 19 is 28 meaning you have to find what multiplies with 3 to get 9 because 19+9 is 28
Hope this helps
What is the range of the function g(x) = |x – 12| – 2?
{y | y > –2}
{y | y > –2}
{y | y > 12}
{y | y > 12}
Answers
The range of the function g(x) = |x - 12| - 2 is {y | y > -2}, indicating that the function can take any value greater than -2.
To find the range of the function g(x) = |x - 12| - 2, we need to determine the set of all possible values that the function can take.
The absolute value function |x - 12| represents the distance between x and 12 on the number line. Since the absolute value always results in a non-negative value, the expression |x - 12| will always be greater than or equal to 0.
By subtracting 2 from |x - 12|, we shift the entire range downward by 2 units. This means that the minimum value of g(x) will be -2.
Therefore, the range of g(x) can be written as {y | y > -2}, which means that the function can take any value greater than -2. In other words, the range includes all real numbers greater than -2.
Visually, if we were to plot the graph of g(x), it would be a V-shaped graph with the vertex at (12, -2) and the arms extending upward infinitely. The function will never be less than -2 since we are subtracting 2 from the absolute value.
for similar questions on range of the function.
https://brainly.com/question/29017978
#SPJ8
What made the American "Declaration of Independence" document - and later the
French counterpart of the "Declaration of the Rights of Man" - so radically influential in
the late 18th century?
1. It was the first time a group of subjects challenged the absolute authority of a king and
ultimately obtained their independence. The French case also echoed that challenge against
established rule of absolute monarchy.
2. It constituted the first instance where propaganda was used to rally the people behind a cause
for change. These documents were pamphlets that were circulated among the populace, but
nothing more after the revolution.
3. It was a popular call for support of the status quo in the form of absolute monarchy - through
King George III in England and King Louis XIV in France. The people sought to reinforce their
monarchs' powers in order to protect their country from foreign invasion.
Answers
The American "Declaration of Independence" and French "Declaration of the Rights of Man" were so radically influential in the late 18th century because it was the first time a group of subjects challenged the absolute authority of a king.
In the 18th century, many countries were still under absolute monarchy. The monarchy involved a king who had absolute authorities a group of noblemen who rule with the king.
However, the American "Declaration of Independence" and the French "Declaration of the Rights of Man" were so radically influential in the late 18th century because it was the first time a group of subjects challenged the absolute authority of a king and ultimately obtained their independence. The French case also echoed that challenge against established rule of absolute monarchy.
Learn more about American declaration of independence: https://brainly.com/question/24938419
when a function is invoked with a list argument, the references of the list is passed to the functiontrue/false
Answers
The answer is true. When a function is invoked with a list argument in Python, the reference to the list is passed to the function.
Is it true that when a list is passed as an argument to a function its reference is passed to the function?This means that any changes made to the list within the function will affect the original list outside of the function as well.
Here's an example to illustrate this behavior:
def add_element(lst, element):
lst.append(element)
my_list = [1, 2, 3]
add_element(my_list, 4)
print(my_list) # Output: [1, 2, 3, 4]
In this example, the add_element function takes a list (lst) and an element (element) as arguments and appends the element to the end of the list.
When the function is called with my_list as the first argument, the reference to my_list is passed to the function.
Therefore, when the function modifies lst by appending element to it, the original my_list list is also modified. The output of the program confirms that the original list has been changed.
It's important to keep this behavior in mind when working with functions that take list arguments, as unexpected modifications to the original list can lead to bugs and errors in your code.
Learn more about function
brainly.com/question/12431044
#SPJ11
Tyler’s cell phone has a $50 charge each month, but no initial fee. On the same coordinate plane, graph the cost of Tyler’s cell phone plan over a period of two years. Then describe how the two graphs are the same and how they are different
Answers
use the values of the vertex and point to write the equation of the graph in standard form

Answers
The vertex form of a quadratic function is:
\(\begin{gathered} y=a(x-h)^2+k \\ \text{ Where} \\ (h,k)\text{ is the vertex of the parabola } \end{gathered}\)The standard form of a quadratic function is:
\(y=ax^2+bx+c\)We can do the following steps to solve the exercise.
Step 1: We replace the values of h,k, x, and y into the vertex form of a quadratic equation, and we solve for a.
\(\begin{gathered} h=1 \\ k=-5 \\ x=3 \\ y=-1 \end{gathered}\)\(\begin{gathered} y=a(x-h)^{2}+k \\ -1=a(3-1)^2-5 \\ -1=a(2)^2-5 \\ -1=4a-5 \\ \text{ Add 5 from both sides} \\ -1+5=4a-5+5 \\ 4=4a \\ \text{ Divide by 4 from both sides} \\ \frac{4}{4}=\frac{4a}{4} \\ 1=a \end{gathered}\)Step 2: We replace the values of a,h, and k into the vertex form of a quadratic equation.
\(\begin{gathered} y=a(x-h)^{2}+k \\ y=1(x-1)^2-5 \end{gathered}\)Step 3: We expand the expression inside the parentheses and combine like terms to convert the function into its standard form.
\(\begin{gathered} y=1(x-1)^{2}-5 \\ y=(x-1)^2-5 \\ y=(x-1)(x-1)-5 \\ \text{ Apply the distributive property} \\ y=x(x-1)-1(x-1)-5 \\ y=x*x-x*1-1*x-1*-1-5 \\ y=x^2-x-x+1-5 \\ y=x^2-2x-4 \end{gathered}\)AnswerThe equation of the graph in standard form is:
\(y=x^{2}-2x-4\)Find the set of values if x for which each of the following is increasing. I know that answer is supposed to be x<-1.75 but I’m not sure how to get that and need help is possible. Thank you.
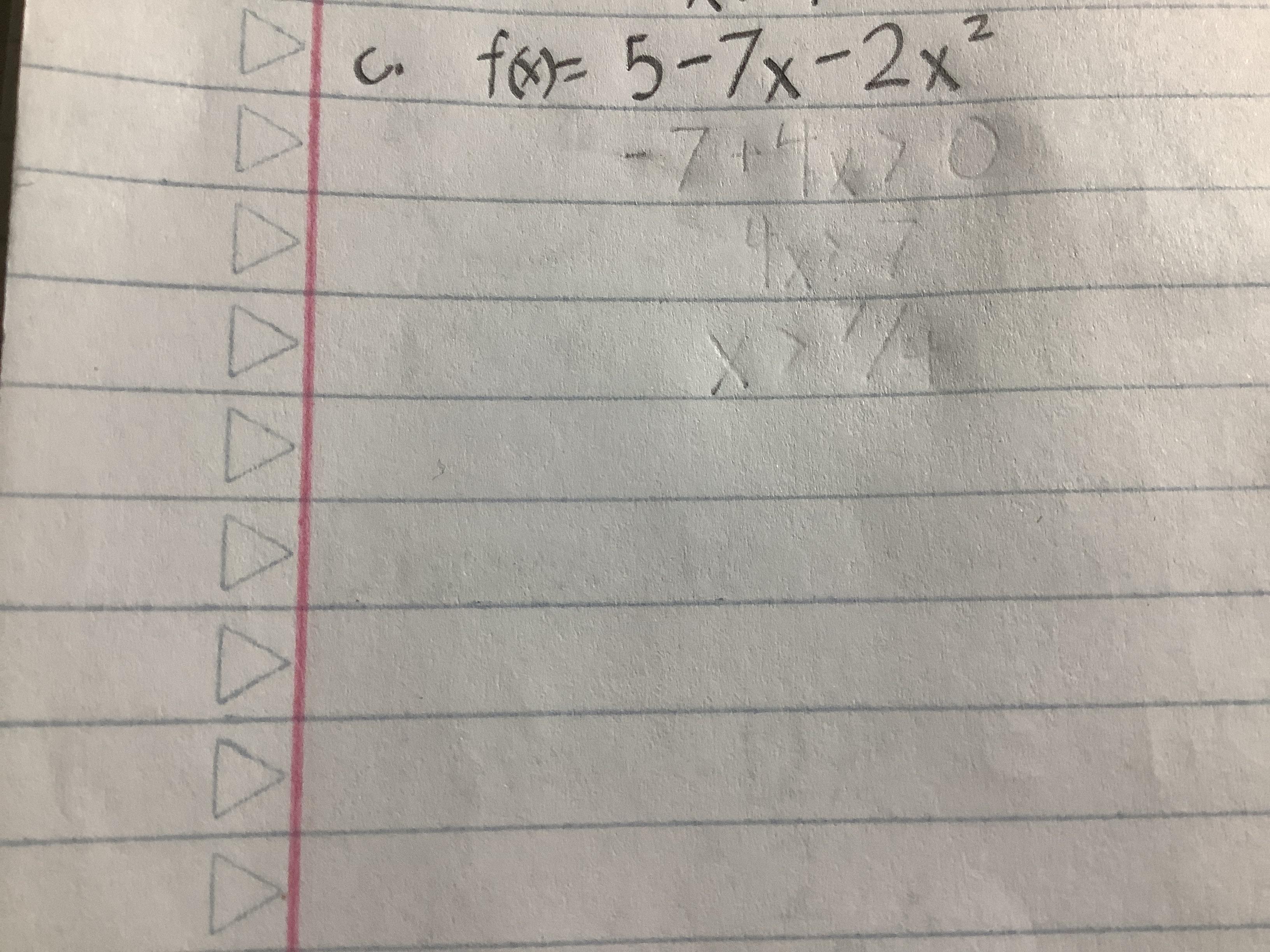
Answers
Answer:
The general form of a quadratic equation is ax^2 + bx + c = y. From the equation for c, our a is -2, our b is -7 and our c is 5.
When a < 0, the function opens downward and has a maximum for its vertex.
When a quadratic function has maximum, its x values will always be increasing from negative infinity to the x-coordinate of the maximum (You can also simply write x < x coordinate of the maximum as you've already done).
We can find the x-coordinate of the maximum using the equation
\(-b/2a\)
Thus, since b is -7 and a is -2, we have
\(-(-7)/2(-2)\\7/-4\\-7/4=-1.75\)
This is how you get that the function is increasing from x < -1.75.
The green line in the attached picture also highlights the same idea.

find the average value of f over the given rectangle. f(x, y) = 5ey x + ey , r = [0, 6] ⨯ [0, 1]
Answers
The average value of f over the rectangle [0,6] x [0,1] is approximately 3.427.
The average value of a function f over a rectangle R is given by:
avg(f) = (1/Area(R)) * double integral of f over R
Here, f(x,y) = 5e^(yx) + e^y and R = [0,6] x [0,1]
The area of R is given by:
Area(R) = (6 - 0) * (1 - 0) = 6
So, the average value of f over R is:
avg(f) = (1/6) * double integral of f over R
We can evaluate the double integral using iterated integration. First, we integrate f with respect to y from 0 to 1, and then integrate the result with respect to x from 0 to 6:
integral of f(x,y) dy = integral of (5e^(yx) + e^y) dy
= (5x/2)e^(yx) + e^y + C
where C is the constant of integration.
Now, we integrate this result with respect to x from 0 to 6:
integral of [(5x/2)e^(yx) + e^y] dx = [(5/2) * integral of xe^(yx) dx] + integral of e^y dx
= [(5/2) * (1/y)e^(yx) - (5/2)(1/y^2)(e^(yx) - 1)] + ey + C
where C is another constant of integration.
Therefore, the average value of f over R is:
avg(f) = (1/6) * [(5/2) * (1/y)e^(yx) - (5/2)(1/y^2)(e^(yx) - 1) + ey] evaluated from y=0 to y=1 and x=0 to x=6
avg(f) = (1/6) * [(5/2) * (1/e^6 - 1) - (5/2)(1/e - 1/e^6) + e - 1]
avg(f) = (1/6) * [(5/2) * (1 - e^-6) - (5/2)(e^-1 - e^-6) + e - 1]
avg(f) = (1/6) * [(5/2) * (1 - e^-6 - e^-1 + e^-6) + e - 1]
avg(f) = (1/6) * [(5/2) * (1 - e^-1) + e - 1]
avg(f) ≈ 3.427
Therefore, the average value of f over the rectangle [0,6] x [0,1] is approximately 3.427.
Learn more about average value here
https://brainly.com/question/30031427
#SPJ11
Determine whether the binomial (x-4) is a factor of the polynomial p(x) = 5x³ - 20x² - 5x+ 20-
Answers
Step-by-step explanation:
IF x-4 is a factor, then putting in x = + 4 will make the polynomial = 0
5 ( 4^3) - 20 (4^2) - 5(4) + 20 = 0 Yes...it is a factor
\(x - 4 = 0 \\ x = 4 \\ \)
substitute value of x in the function to see if it equals to zero , if not it won't be a factor of the function
\(5 {x}^{3} - 20 {x}^{2} - 5x + 20 = 0 \\ 5(4) ^{3} - 20( {4})^{2} - 5(4) + 20 = 0 \\ 5(64) - 20(16) - 20 + 20 = 0 \\ 320 - 320 - 20 + 20 = 0 \\ 0 = 0\)
so (x-4) is a factor for the function
A number is chosen at random from 1 to 50. Find the probability of selecting multiples of 12.
Answers
Answer:
P(multiples of 12)=1/25
Step-by-step explanation:
Multiples of 12: 12, 24, 36, 48
That is 4/50=1/25
2x + 3y = 1240
x = 2y - 10
Answers
Answer:
x = 350, y = 180Step-by-step explanation:
2x + 3y = 1240 and x = 2y - 10
so:
2(2y - 10) + 3y = 1240 4y - 20 + 3y = 1240+20 +20
7y = 1260÷7 ÷7
y = 180x = 2•180 - 10 = 360 - 10 = 350Solve the following first-order DEs: (e2y−ycos(xy))dx+(2xe2y−xcos(xy)+2y)dy=0 (8 pts) x(yy′−3)+y2=0
Answers
1. The solution to the first differential equation is given by e^2yx - ysin(xy) + y^2 + C = 0, where C is an arbitrary constant.
2. The general solution to the second differential equation is x(3x - y^2) = C, where C is a positive constant.
To solve the first-order differential equations, let's solve them one by one:
1. (e^2y - ycos(xy))dx + (2xe^2y - xcos(xy) + 2y)dy = 0
We notice that the given equation is not in standard form, so let's rearrange it:
(e^2y - ycos(xy))dx + (2xe^2y - xcos(xy))dy + 2ydy = 0
Comparing this with the standard form: P(x, y)dx + Q(x, y)dy = 0, we have:
P(x, y) = e^2y - ycos(xy)
Q(x, y) = 2xe^2y - xcos(xy) + 2y
To check if this equation is exact, we can compute the partial derivatives:
∂P/∂y = 2e^2y - xcos(xy) - sin(xy)
∂Q/∂x = 2e^2y - xcos(xy) - sin(xy)
Since ∂P/∂y = ∂Q/∂x, the equation is exact.
Now, we need to find a function f(x, y) such that ∂f/∂x = P(x, y) and ∂f/∂y = Q(x, y).
Integrating P(x, y) with respect to x, treating y as a constant:
f(x, y) = ∫(e^2y - ycos(xy))dx = e^2yx - y∫cos(xy)dx = e^2yx - ysin(xy) + g(y)
Here, g(y) is an arbitrary function of y since we treated it as a constant while integrating with respect to x.
Now, differentiate f(x, y) with respect to y to find Q(x, y):
∂f/∂y = e^2x - xcos(xy) + g'(y) = Q(x, y)
Comparing the coefficients of Q(x, y), we have:
g'(y) = 2y
Integrating g'(y) with respect to y, we get:
g(y) = y^2 + C
Therefore, f(x, y) = e^2yx - ysin(xy) + y^2 + C.
The general solution to the given differential equation is:
e^2yx - ysin(xy) + y^2 + C = 0, where C is an arbitrary constant.
2. x(yy' - 3) + y^2 = 0
Let's rearrange the equation:
xyy' + y^2 - 3x = 0
To solve this equation, we'll use the substitution u = y^2, which gives du/dx = 2yy'.
Substituting these values in the equation, we have:
x(du/dx) + u - 3x = 0
Now, let's rearrange the equation:
x du/dx = 3x - u
Dividing both sides by x(3x - u), we get:
du/(3x - u) = dx/x
To integrate both sides, we use the substitution v = 3x - u, which gives dv/dx = -du/dx.
Substituting these values, we have:
-dv/v = dx/x
Integrating both sides:
-ln|v| = ln|x| + c₁
Simplifying:
ln|v| = -ln|x| + c₁
ln|x| + ln|v| = c₁
ln
|xv| = c₁
Now, substitute back v = 3x - u:
ln|x(3x - u)| = c₁
Since v = 3x - u and u = y^2, we have:
ln|x(3x - y^2)| = c₁
Taking the exponential of both sides:
x(3x - y^2) = e^(c₁)
x(3x - y^2) = C, where C = e^(c₁) is a positive constant.
This is the general solution to the given differential equation.
To learn more about derivatives Click Here: brainly.com/question/29144258
#SPJ11
a group of 54 college students from a certain liberal arts college were randomly sampled and asked about the number of alcoholic drinks they have in a typical week. the purpose of this study was to compare the drinking habits of the students at the college to the drinking habits of college students in general. in particular, the dean of students, who initiated this study, would like to check whether the mean number of alcoholic drinks that students at his college in a typical week differs from the mean of u.s. college students in general, which is estimated to be 4.73. the group of 54 students in the study reported an average of 5.
Answers
We do not have sufficient evidence to conclude that the mean number of alcoholic drinks consumed by students at the liberal arts college is significantly different from the mean number consumed by college students in general.
We need to conduct a hypothesis test to determine whether the mean number of alcoholic drinks consumed by students at the liberal arts college is significantly different from the mean number consumed by college students in general.
To conduct the hypothesis test, we need to set up the null and alternative hypotheses.
Null Hypothesis: The mean number of alcoholic drinks consumed by students at the liberal arts college is equal to the mean number consumed by college students in general (μ = 4.73).
Alternative Hypothesis: The mean number of alcoholic drinks consumed by students at the liberal arts college is not equal to the mean number consumed by college students in general (μ ≠ 4.73).
We would then need to calculate the test statistic, which would be a t-score. This can be calculated using the formula:
t = (x bar - μ) / (s / √n)
where x bar is the sample mean (5), μ is the hypothesized population mean (4.73), s is the sample standard deviation, and n is the sample size (54).
Assuming that the sample standard deviation is unknown, we would need to estimate it using the sample data. This gives us:
s = √[Σ(xi - x bar)² / (n - 1)] = 3.05
Plugging in the values, we get:
t = (5 - 4.73) / (3.05 / √54) = 1.67
To determine the p-value, we would need to consult a t-distribution table with 53 degrees of freedom (n - 1). The p-value corresponding to a t-score of 1.67 with 53 degrees of freedom is approximately 0.102.
Since the p-value is greater than the level of significance (α) typically chosen (0.05), we fail to reject the null hypothesis. This means we do not have sufficient evidence to conclude that the mean number of alcoholic drinks consumed by students at the liberal arts college is significantly different from the mean number consumed by college students in general.
To learn more about null hypothesis, click here: brainly.com/question/4436370
#SPJ11
two cards are selected in a sequence from a standard deck. what is the probability that the second card is a jack given that the first card was a 2. (assume the 2 was not replaced.)
Answers
The probability that the second card is a jack given that the first card was a 2 is 52/51.
To calculate the probability that the second card is a jack given that the first card was a 2, we need to consider the remaining cards in the deck after the first card is drawn.
When the first card is drawn and it is a 2, there are 51 cards remaining in the deck, out of which there are 4 jacks.
The probability of drawing a jack as the second card, given that the first card was a 2, can be calculated using conditional probability:
P(Second card is a jack | First card is a 2) = P(Second card is a jack and First card is a 2) / P(First card is a 2)
Since the first card is already known to be a 2, the probability of the second card being a jack and the first card being a 2 is simply the probability of drawing a jack from the remaining 51 cards, which is 4/51.
The probability of the first card being a 2 is simply the probability of drawing a 2 from the initial deck, which is 4/52.
P(Second card is a jack | First card is a 2) = (4/51) / (4/52)
Simplifying the expression:
P(Second card is a jack | First card is a 2) = (4/51) * (52/4)
P(Second card is a jack | First card is a 2) = 52/51
To learn more about probability click here:
brainly.com/question/30736116
#SPJ11
put these fractions in order of size, smallest to largest 1/3 2/5 3/8
Answers
Answer:
3/8, 2/5, 1/3
Step-by-step explanation:
From smallest to largest is 3/8 2/5 1/3
40 fl oz = _ c 9 gal=__ qt
Answers
The spinner is equally likely to land on any of the five sections. a spinner contains 5 equals sections labeled 1, 2, 3, 4, 5. sections 2, 1, 5, 4 are shaded. what is the probability that the spinner lands on an even number or on the unshaded section?
Answers
Answer:
3/5
Step-by-step explanation:
the chance of landing on an even number (2 or 4) is 2/5
the chance of landing on the unshaded section (3) is 1/5
add the 2 together since the problem said "or" to get 3/5