According to the graph, what is the value of the constant in the equation below?
A. 2
B. 0.5
C. 1
D. 5

Answers
Answer:
A
Step-by-step explanation:
Take any point which lies on the line.
Let's take (2, 4).
Solving :
⇒ Height = Constant × Width
⇒ 4 = Constant × 2
⇒ Constant = 2
The constant value in the equation ss 2.
Option A is the correct answer.
What are coordinates in a graph?The coordinates in a graph indicate the location of a point with respect to the x-axis and y-axis.
The coordinates in a graph show the relationship between the information plotted on the given x-axis and y-axis.
We have,
Coordinates from the graph.
= (2, 4) and (3, 6)
Now,
Height = constant x width
(2, 4) = (width, height)
So,
4 = constant x 2
constant = 4/2
constant = 2
Thus,
The constant value is 2.
Learn more about coordinates here:
https://brainly.com/question/13118993
#SPJ2
Related Questions
The ceiling of victorias living room is a square that is 15⟌2 ft long on each side. to decorate for a party, she plans to hang crepe paper around the perimeter of the ceiling and then from each corner to the opposite corner. Victoria can buy rolls that each contain 30 ft of crepe paper. What is the minimum number of rolls she should buy? Show your work.
Answers
Answer:
5 rolls.
Step-by-step explanation:
The perimeter of a two-dimensional shape is the distance all the way around the outside.
Given the square ceiling has side lengths of 15√2 feet, and the side lengths of a square are equal, the perimeter of the ceiling is:
\(\implies 4 \times 15\sqrt{2}=60\sqrt{2}\;\; \sf ft\)
Diagonal of a square
\(d=\sqrt{2s^2}\)
where s is the side length.
Therefore, the length of the diagonal of the ceiling is:
\(\implies d=\sqrt{2(15\sqrt{2})^2}\)
\(\implies d=\sqrt{2\cdot 450}\)
\(\implies d=\sqrt{900}\)
\(\implies d=30\;\; \sf ft\)
Therefore, the total amount of crepe paper Victoria needs is:
\(\begin{aligned}\implies \sf Total\;length&=\sf Perimeter+2\;diagonals\\&=60\sqrt{2}+30+30\\&=144.8528137...\;\; \sf ft\end{aligned}\)
If each roll contains 30 ft, to calculate the minimum number of rolls Victoria should buy, divide the total amount of crepe paper by 30 and round up to the nearest whole number:
\(\implies \dfrac{144.8528137...}{30}=4.828427125...\)
Therefore, Victoria should buy a minimum of 5 rolls of crepe paper.
Answer:
5 rolls
Step-by-step explanation:
We are here given that the length of a ceiling which is square in shape is 15√2 ft .
She wants to decorate her ceiling with crepe paper around the perimeter and from each corner to the opposite corners ( this means along the diagonals of the wall ) For figure see attachment.
So from the figure th total length of crepe paper required will be ,
l = AB + BC + CD + DA + BD + AC . . . . . (i)
and here AC = BC = CD = DA = 15√2 ft .
Also BD = AC [ as the diagonals of a square are equal]
So , we can write (i) as ,
l = 4*AB + 2*AC
In right angled triangle BDC ,
BC² + CD² = BD² [ Pythagoras theorem]
(15√2ft)² + (15√2ft)² = BD²
450ft2 + 450ft² = BD²
900ft² = BD²
√900ft² = BD²
30ft = BD
So total length of crepe paper required will be,
l = 4*15√2 ft + 2*30ft
l = 60*1.4141ft + 60ft
l = 84.84ft + 60ft
l = 144.84ft
Now we are here given that the length of each roll is 30ft . So total number of such roles that will be required is ,
n = 144.84ft / 30ft
n = 4.828 rolls
n ≈ 5 rolls
and we are done!

How can you use a rectangle to calculate the slope of a line ?
Answers
Answer:
The slope is the inclination of a surface or a line with respect to the horizontal. It can be measured at an angle in degrees, radians or grades or even in percentage, that is to say according to the height to length ratio multiplied by 100.
Step-by-step explanation:
when u, v are nonzero vectors, then span{u, v} contains the line through u and the origin, as well as the line through v and the origin.
Answers
The span of the two vectors is the set of all linear combinations of the two vectors. This means that any point on the line through u and the origin, as well as any point on the line through v and the origin, can be written as a linear combination of u and v.
1. Start by taking two non-zero vectors u and v.
2. The span of the two vectors is the set of all linear combinations of the two vectors, which means that any point on the line through u and the origin, as well as any point on the line through v and the origin, can be written as a linear combination of u and v.
3. Therefore, span{u, v} contains the line through u and the origin, as well as the line through v and the origin.
The span of two non-zero vectors u and v contains the line through u and the origin, as well as the line through v and the origin. Any point on these two lines can be written as a linear combination of u and v.
Learn more about vector here
https://brainly.com/question/15709504
#SPJ4
6 3/4 divided by 4 1/2=
Answers
Answer:
1 1/2
Step-by-step explanation:
Hi there,
First convert your fractions to mixed numbers:
27/4 and 9/2
Then multiply
(remember to flip second fraction over)
27/4 x 2/9
You would get 54/36,
Now simplify 54/36
1 1/2
What is an example of "an enumeration of its range {aξ : ξ < α}"?

Answers
An example of "an enumeration of its range {aξ : ξ < α}" in this case would be the list of natural numbers {0, 1, 2, 3, ...}, which represents the ordinal numbers less than ω^2.
How to determine an example of "an enumeration of its range {aξ : ξ < α}"An example of "an enumeration of its range {aξ : ξ < α}" can be found in the context of ordinal numbers.
Let's consider the ordinal number α = ω^2, where ω represents the first infinite ordinal (the set of all natural numbers). In this case, the range {aξ : ξ < α} refers to the collection of all ordinal numbers that are less than α.
The ordinal numbers less than ω^2 can be enumerated as follows:
a0 = 0
a1 = 1
a2 = 2
...
an = n
...
Each natural number n corresponds to an ordinal number less than ω^2. The enumeration continues indefinitely, as there are infinitely many ordinal numbers less than ω^2.
So, an example of "an enumeration of its range {aξ : ξ < α}" in this case would be the list of natural numbers {0, 1, 2, 3, ...}, which represents the ordinal numbers less than ω^2.
Learn more about range at https://brainly.com/question/26098895
SPJ1
A young female lion was brought into the wildlife zoo weighing 53.5 pounds. After two years, she weighed 5.5 times
that amount. Which is the most logical estimated product for the weight of the lion after two years of captivity?
O 3 pounds
O 32 pounds
324 pounds
3240 pounds
Answers
Answer:
324
Step-by-step explanation:
This is because when rounding you multiply 55 by 6 that is equal to 330 which is near 324. However if you want the answer spot on it would be 294
Answer:
324
Step-by-step explanation:
so you would times 53.5 by 5.5 and you would get 294.25 so i rounded up and the most logical estimation there was is 324 pounds
wants to tile the surface of a rectangular storage case that is inches long, inches wide, and inches tall. If he uses all green tiles, how many tiles will he need?
Answers
The surface area of the rectangular prism is 396 square inches
He will need 504 tlles
What is the surface area of the rectangular prism?From the question, we have the following parameters that can be used in our computation:
7 in by 12 in by 6 in
The surface area of the rectangular prism is calculated as
Area = 2 * (7 * 12 + 7 * 6 + 12 * 6)
Evaluate
Area = 396
Hence, the area is 396 square inches
The number of tiles is 7 * 12 * 6 = 504
Read more about surface area at
brainly.com/question/26403859
#SPJ1
Question
wants to tile the surface of a rectangular storage case that is 7 inches long, 12 inches wide, and 6 inches tall. If he uses all green tiles, how many tiles will he need?
Verify the identity. Sin 4x= 2 sin 2x cos 2x
Answers
Answer:
2=4x/2x
2=2x
x=2/2
x=1
Answer:
Step-by-step explanation:
sin(a+b)=sin(a)cos(b)+cos(a)(sin(b)
sin(4x)=sin(2x+2x)
sin(2x+2x)=sin(2x)×cos(2x)+cos(2x)×sin(2x)
simplified to
2sin(2x)cos(2x)
Help me out here pleaseeeeeeee

Answers
Answer: \(3\frac{1}{5}\)
have: \(6\frac{1}{2}=6.5;\\\\3\frac{3}{10}=3.3\)
Syd ran than Jose: \(6.5-3.3=3.2=\frac{16}{5}=3\frac{1}{5}\) (miles)
Step-by-step explanation:
Answer:
\(3\frac{1}{5}\)
Step-by-step explanation:
First you want to find the least common denominator so we can figure out this problem.
We have \(3\frac{3}{10} , 6\frac{1}{2}\) so all we need to do is multiply ONLY the fraction next to the 6 so we can figure out what 1/2 and 3/10 correlates to which you will get
By multiplying by 5 you can get the same equation so the common denominator relates to one another.You get 5 by doing 10/2 which is 5.so your new question is
\(3\frac{3}{10} , 6\frac{5}{10}\)
Which is so much easier, all you need to do is subtraction between the two!
5/10-3/10 is 2/10
2/10=1/5
Then we got the whole numbers
6-3=3
so the answer is \(3\frac{1}{5}\)
consider the following statement. passing a comprehensive exam is a necessary condition for obtaining a master's degree. which of the following correctly expresses this statement in if-then form? (select all that apply.) if a person does not pass a comprehensive exam, then that person cannot obtain a master's degree. if a person obtained a master's degree, then that person passed a comprehensive exam. if a person does not pass a comprehensive exam, then that person can obtain a master's degree. if a person cannot obtain a master's degree, then that person passed a comprehensive exam. if a person passed a comprehensive exam, then that person obtained a master's degree.
Answers
The statements which correctly express the given statement in if-then form is “if a person does not pass a comprehensive exam, then that person cannot obtain a master's degree”, “if a person obtained a master's degree, then that person passed a comprehensive exam”, and “if a person passed a comprehensive exam, then that person obtained a master's degree.” (Option A, B, and E)
An if-then form of a statement, also called a conditional statement, refers to a statement in which a hypothesis is given followed by a conclusion. The statement read as “if p then q”.
The first part of the statement is the hypothesis or “if,” component of a conditional statement. The second part of the statement is the conclusion or “then,” component of a conditional statement.
Hence, the conclusion is the result of a hypothesis. The given statement is that passing a comprehensive exam is a necessary condition for obtaining a master's degree. Hence, passing a comprehensive exam and obtaining a master’s degree are connected to each other and either can be used as a hypothesis with the other as conclusion. Hence the statements which correctly express the given statement in if-then form are “if a person does not pass a comprehensive exam, then that person cannot obtain a master's degree”, “if a person obtained a master's degree, then that person passed a comprehensive exam”, and “if a person passed a comprehensive exam, then that person obtained a master's degree.”
Learn more about If-then form:
https://brainly.com/question/2397989
#SPJ4
What is the meaning of "unique"?

Answers
Answer:
In this context, unique means existence of only one value for that element and no more than one value
Step-by-step explanation:
3 bananas cost $0.33. At this rate, how much do 5 bananas cost?
Answers
One banana cost $0.11
0.11 * 5 = $0.55 for 5 bananas
Please help me I wanna get out this class
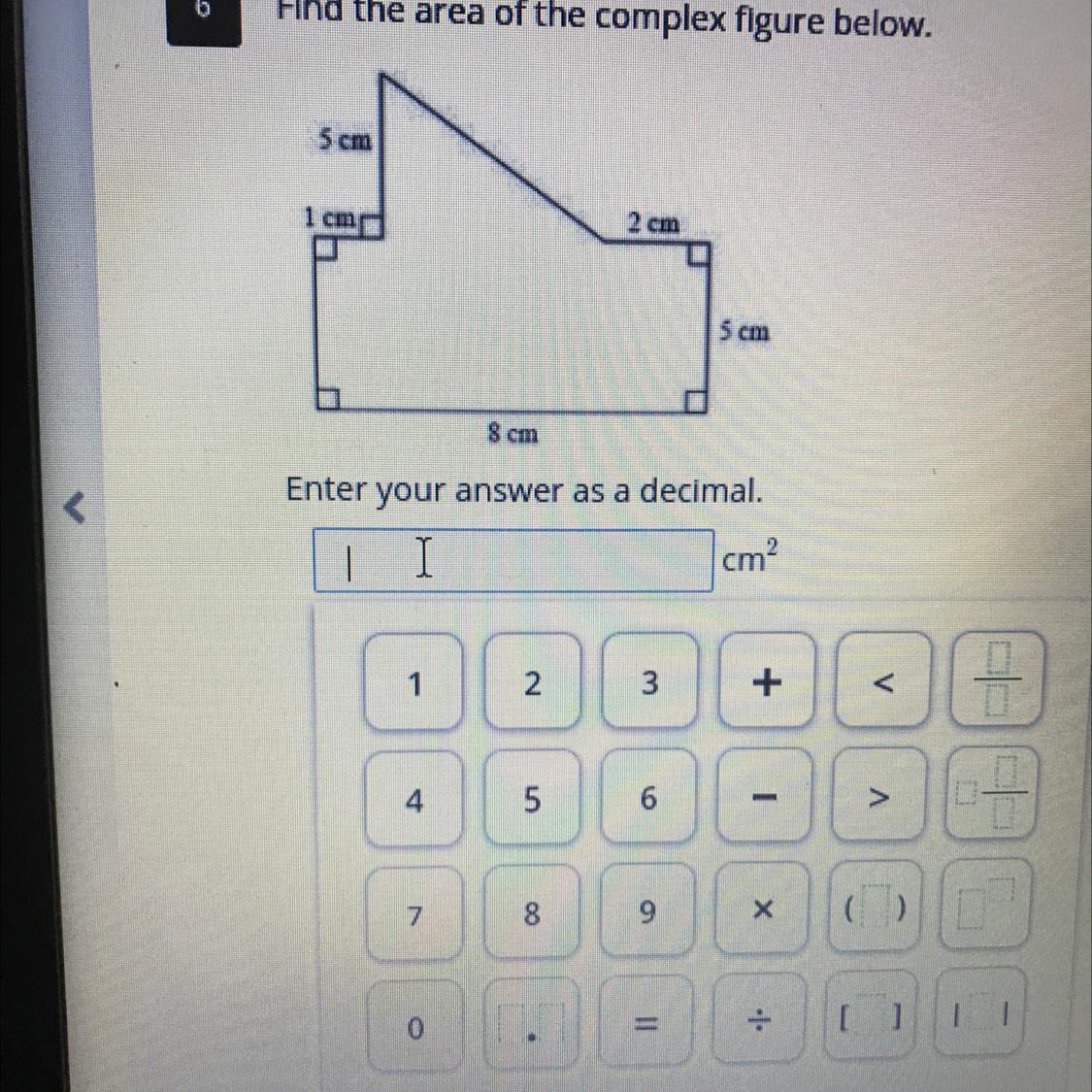
Answers
area of rectangle is length x width
8x5=40
area of triangle is base x height divide by 2
5x5=25
25 divide by 2 is 12.5
add them together
40+12.4 = 52.4
how do you find the total surface area of a pyramid
Answers
Answer:
To find the total surface area of a pyramid you do SURFACE AREA =B+12(P×l)
An NCAA study reported that the average salary of the 300 major college football coaches is $1.47 million. Using a random sample of 30 coaches and a population standard deviation of $300,000, what is the probability that the sample mean is between $1.4 million and $1.5 million per year?
Answers
Answer:
60.85% probability that the sample mean is between $1.4 million and $1.5 million per year
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal probability distribution
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
In this question, we have that:
In millions of dollars.
\(\mu = 1.47, \sigma = 0.3, n = 30, s = \frac{0.3}{\sqrt{30}} = 0.0548\)
What is the probability that the sample mean is between $1.4 million and $1.5 million per year?
This is the pvalue of Z when X = 1.5 subtracted by the pvalue of Z when X = 1.4. So
X = 1.5
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{1.5 - 1.47}{0.0548}\)
\(Z = 0.55\)
\(Z = 0.55\) has a pvalue of 0.7088
X = 1.4
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{1.4 - 1.47}{0.0548}\)
\(Z = -1.28\)
\(Z = -1.28\) has a pvalue of 0.1003
0.7088 - 0.1003 = 0.6085
60.85% probability that the sample mean is between $1.4 million and $1.5 million per year
Answer:
\( z= \frac{1.4-1.47}{\frac{0.3}{\sqrt{30}}}= -1.278\)
\( z= \frac{1.5-1.47}{\frac{0.3}{\sqrt{30}}}= 0.548\)
And we can find the probability with this difference:
\( P(-1.278<z<0.548) = P(z<0.548) -P(z<-1.278) =0.708-0.101= 0.607\)
So then the probability that the sample mean is between $1.4 million and $1.5 million per year is 0.607
Step-by-step explanation:
For this case we have the following info given:
\( \mu = 1.47\) the true mean for the problem
n =30 represent the sample size
\( \sigma = 0.3 millions\) represent the population deviation
And we want to find this probability
\( P(1.4< \bar X <1.5)\)
And we can use the z score given by:
\( z= \frac{\bar X -\mu}{\frac{\sigma}{\sqrt{n}}}\)
And if we find the z scores for the limits we got:
\( z= \frac{1.4-1.47}{\frac{0.3}{\sqrt{30}}}= -1.278\)
\( z= \frac{1.5-1.47}{\frac{0.3}{\sqrt{30}}}= 0.548\)
And we can find the probability with this difference:
\( P(-1.278<z<0.548) = P(z<0.548) -P(z<-1.278) =0.708-0.101= 0.607\)
So then the probability that the sample mean is between $1.4 million and $1.5 million per year is 0.607
Where is the central tendency located in a skewed left distribution?
to the left of the tallest bar
to the right of the smallest bar
to the left of the smallest bar
in the center of the graph
to the right of the tallest bar
Answers
The Central tendency is typically located to the right of the tallest bar.
In a skewed left distribution, the central tendency is typically located to the right of the tallest bar. Skewed left distributions, also known as negatively skewed distributions, are characterized by a tail that extends towards the left side of the distribution.
The central tendency refers to the measure that represents the center or average of a distribution. It provides information about the typical or central value around which the data points tend to cluster. Common measures of central tendency include the mean, median, and mode.
In a skewed left distribution, the mean is usually influenced by the long tail on the left side of the distribution. This tail pulls the mean towards lower values, resulting in a lower mean compared to the median. Therefore, the mean will typically be located to the left of the tallest bar in a skewed left distribution.
On the other hand, the median is less affected by the skewness of the distribution and is relatively robust to extreme values. It represents the value that separates the lower 50% of the data from the upper 50%. In a skewed left distribution, the median will be located closer to the tallest bar or even slightly to the right of it.
The mode, which represents the most frequently occurring value in a distribution, may or may not be influenced by the skewness depending on the shape of the distribution. It can be located anywhere along the distribution, and its position is not necessarily tied to the location of the tallest bar.
To summarize, in a skewed left distribution, the central tendency is typically located to the right of the tallest bar. The median is usually closer to the tallest bar or slightly to the right, while the mean is influenced by the skewness and tends to be located to the left of the tallest bar.
To know more about Central tendency.
https://brainly.com/question/1288901
#SPJ8
There are 15 pieces of fruit in a bowl and 6 of them are apples. What percentage of the pieces of fruit in the bowl are apples?
Answers
40%
6/15 is 0.4. Multiplied by 100, that makes 40%.
plz help me with these two questions ( show work plz)

Answers
Step-by-step explanation:
3. 7 = -2y + 4
2y = 4 - 7
2y = -3
y = -1.5
5. -3x - 2 = -17
17 - 2 = 3x
15 = 3x
3x = 15
x = 15/3
x = 5
A line Ax +3y-6=0 is perpendicular to the line 5x+7y-
k=0. If 5x+7y-k=0 passes through the point (4,3).
Determine the values of A and K
(4mks)
Answers
Answer:
ba
Step-by-step explanation:
ba
Select the correct answer. Joel and Kevin are each putting money in a savings account to buy a new bicycle. The amount, in dollars, in Joel's savings account, x weeks after the start of the year, is modeled by function j. The amount of money in Kevin's account, at the same time, is modeled by function k. j(x) = 25 + 3x k(x) = 15 + 2x Which function correctly represents how much more money, in dollars, is in Joel's account than in Kevin's account x weeks after the start of the year? O A. (j − k)(x) = 40 + 5x (j − k)(x) = 40 + x (j-k)(x) = 10 + 5x (j-k)(x) = 10 + x O B. C. O D. Reset dtry Next
Answers
The correct answer is (j - k)(x) = 10 + x.
To find the difference in the amount of money between Joel's and Kevin's accounts, we subtract the value of Kevin's account (k(x)) from Joel's account (j(x)).
(j - k)(x) = (25 + 3x) - (15 + 2x)
= 25 - 15 + 3x - 2x
= 10 + x
This expression represents how much more money is in Joel's account compared to Kevin's account after x weeks.
Therefore, the correct function is (j - k)(x) = 10 + x.
for such more question on Kevin's account
https://brainly.com/question/26866234
#SPJ11
y
8
2
16
4
32
8
Find the constant of proportionality (r) in the equation y=rn.
MY
T=
Co
Your Jinswer should be
a simplified proper fraction, like 3/5
a simplified improper fraction, like 74
Stucl
MY
Pro
Answers
Answer:
86
Step-by-step explanation:
Having trouble with this, help please?

Answers
Answer:
a) \(7x-15=20\)
b) \(\frac{20+15}{7}\)
c) \(5\)
Step-by-step explanation:

Find each value given the following function:

Answers
Answer:
Step-by-step explanation:
1) f(-4) --> if x < or equal to 3
2) 1/(-4)-4
3) The answer is - 1/8
Each side length of a triangle is 4 cm. What type of triangle is it?
☐ right
□acute
Equilateral
Isosceles
Answers
Answer: Equilateral
Step-by-step explanation:
It's equilateral because it says that each side of the triangle is 4cm. In simple words, all the sides of triangle are equal. Such a triangle is called an equilateral triangle.
Hope you understood.
HELP HELP
Tommy rides in a motorboat against a river current for 25 km. Then he returns to his starting point by floating down river on a raft. Tommy travels 10 hours less on the motorboat than on the raft. Find the speed of the river current if the speed of the motorboat in still water is 12 km/h.
Answers
The speed of current is \(\rm 2 \:km/h\).
What is the relation between distance,speed and time?The relationship between distance, time and speed can be presented as:
\(\begin{aligned} \rm Distance &= Speed \times Time\\\\Speed &= \dfrac{\rm Distance}{Time} \\\\\rm Time &= \dfrac{\rm Distance}{\rm Speed} \end\)
Calculations:
Given:
\(\begin{aligned} \rm Distance\: traveled\: on\: motorboat &= 25\:km\\\rm Speed\:of\:motorboat\:in\:still\:water &= 12\:km/h \end\)
Let the speed of the current be \(\rm x\)
The speed of the boat traveling against the current is \({(12 -\rm x) km/h}\)
Time spent on motorboat is 10 hours less than time spent on raft.
Therefore:
\(\rm \dfrac{25km}{x\:km/h} - \dfrac{25km}{(12 - x)km/h} = 10\)
The equation obtained will be:
\(\dfrac{25}{\rm x} - \dfrac{25}{(12-\rm x)} - = 10\)
Multiplying both sides of the equation by \(\rm x(12 - x )\)
\(\begin{aligned} \rm 25(12 - x) - 25x &= 10\times \rm x(12 - x)\\\\300 - 25x - 25x &= 120x - 10x^2\\\\300 - 50x &= 120x - 10x^2\\\\10x^2 - 120x - 50x + 300 &= 0\\\\10x^2 - 170x +300 &= 0\end\)
Dividing the equation by 10
\(\rm x^2 - 17x + 30 = 0\)
On factoring the equation,
\(\rm =x^2 - 2x -15x + 30 = 0\\\\=x(x - 2) -15(x - 2)\\\\=(x - 2)(x - 15)\)
The values of x is 2 and 15.
Since speed of current i.e \((12 -\rm x)km/h\) cannot be negative, \(\rm x = 2\) is the only acceptable value.
Therefore the speed of current is 2 km/h.
Learn more about the topic here:
https://brainly.com/question/2292310
•Mr. Jones and Mr. Thomas
entered into partnership
I with capital of $12600
and $19200 respectively.
after 3 months they!
were joined by Mr.Forson with a capital of $ 16200.It is agreed that the profit should be shared in proportion to their capitals.During the first 3 month of the year,………..
Answers
The profit should be shared in proportion to Mr Jones, Mr Thomas and Mr forson capitals in the ratio 21 : 32 : 27 respectively.
ProportionMr Jones capital = $12600Mr Thomas capital =$19200Mr forson capital = $16200Total capital = $12600 + $19200 + $16200
= $48,000
Mr Jones proportion = $12600 / $48,000
= 21/80
Mr Thomas proportion = $19200 / $48,000
= 32/80
Mr forson proportion = $16200 / $48000
= 27/80
Learn more about proportion:
https://brainly.com/question/1781657
#SPJ1
Select the correct answer.
If no denominator equals zero, which expression is equivalent to 15/x-6 + 7/x+6?
A.
OB.
OC.
OD.
22 +132
²36
22-48
236
22
C.36
22 +48
²36

Answers
The expression in the options which is equivalent to the given expression is D. (22x + 48) / (x² - 36).
Given expression is,
[15 / (x - 6)] + [7 / (x + 6)]
Cross multiplying the two fractional expressions,
= [15 (x + 6) + 7 (x - 6)] / [(x - 6) (x + 6)]
= [15x + 90 + 7x - 42] / [x² - 6²]
= (22x + 48) / (x² - 36)
Hence the equivalent expression is D.
Learn more about Expressions here :
https://brainly.com/question/28170201
#SPJ1
(9x-4)°
(3x+ 14)°
solve for x=
don’t understand how to find the answer

Answers
Answer:
x=3
Step-by-step explanation:
Simplifying
9x + -4 = 3x + 14
Reorder the terms:
-4 + 9x = 3x + 14
Reorder the terms:
-4 + 9x = 14 + 3x
Solving
-4 + 9x = 14 + 3x
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-3x' to each side of the equation.
-4 + 9x + -3x = 14 + 3x + -3x
Combine like terms: 9x + -3x = 6x
-4 + 6x = 14 + 3x + -3x
Combine like terms: 3x + -3x = 0
-4 + 6x = 14 + 0
-4 + 6x = 14
Add '4' to each side of the equation.
-4 + 4 + 6x = 14 + 4
Combine like terms: -4 + 4 = 0
0 + 6x = 14 + 4
6x = 14 + 4
Combine like terms: 14 + 4 = 18
6x = 18
Divide each side by '6'.
x = 3
Simplifying
x = 3
Answer:
x = 3Explanation:
Write your equation
(3x + 14) = (9x - 4)Subtract 9x from both sides
3x + 14 − 9x = 9x − 4 − 9x
−6x + 14 = −4
Subtract 14 from both sides
−6x + 14 − 14 = −4 − 14
−6x = −18
Divide both sides by -6
−6x / -6 = −18 / -6
x = 3[ zyxx ]
A sequence can be generated by using an= 3an-1, where a1 = 10 and n is a whole number greater than 1.
What are the first 3 terms in the sequence?
A. 3, 13, 23
B. 10, 30, 90
C. 10, 13, 16
D. 3, 30, 300

Answers
Answer:
B
Step-by-step explanation:
using the recursive rule \(a_{n}\) = 3\(a_{n-1}\) and a₁ = 10, then
a₁ = 10
a₂ = 3a₁ = 3 × 10 = 30
a₃ = 3a₂ = 3 × 30 = 90
the first 3 terms are 10 , 30 , 90
Find the equation of the line.
Use exact numbers.
y= __x+__

Answers
Answer:
y = -1/3x + 5
Step-by-step explanation:
y-intercept: 5
Slope: -1/3x