Alfonso uses a payroll deduction to deposit $120 into his
savings account each month. How much will he save in a year?
Please help
Answers
Alfonso will save $120 x 12 = $1,440 in a year. If Alfonso saves $120 each month, his savings after the first month will be $120. After the second month, he will have saved $240 ($120 + $120).
After the third month, he will have saved $360 ($120 + $120 + $120), and so on. After the twelfth month, he will have saved $1,440 ($120 x 12), which is the total amount he saves in a year. This calculation assumes that Alfonso does not withdraw any money from his savings account during the year.
In summary, Alfonso will save $1,440 in a year by depositing $120 into his savings account each month.
Learn more about savings accounts here:- brainly.com/question/29890420
#SPJ11
Related Questions
Parallel to y=−3x−2, through (-3, -3)
Answers
Answer:
Use the formula y-y1=m(x-x1) <---memorize this. The m here is the slope.
Step-by-step explanation:
The equation is in y=mx+b form
Remember mx=slope and b=y-intercept
The question wants you to find the equation that is Parallel to y=-3x-2 and passes through (-3,-3)=(x1,y1)
Parallel=same slope -3x
So now all that's left is to plug into the equation.
y-(-3)=-3(x-(-3))
y+3=-3(x+3) ----> positive - a negative = positive so x-(-x)=x+x
y+3=-3x-9 ----> distribute like terms(subtract 3 from 3 and 3 from -9)
y=-3x-12 - This is your answer, you can check by graphing it.
Could i get Brainlest? thx :)
The perimeter of a rectangular lawn i 50 meter. It' 16 meter long how wide i it?
Answers
The width of the rectangle is 9 meter.
Now, According to the question:
The perimeter of a rectangle is defined as the sum of all the sides of a rectangle. For any polygon, the perimeter formulas are the total distance around its sides. In case of a rectangle, the opposite sides of a rectangle are equal and so, the perimeter will be twice the width of the rectangle plus twice the length of the rectangle and it is denoted by the alphabet “p”.
Now, Solving the problem:
Perimeter of rectangle is 50 meter sq.
Length of the rectangle(L) is 16 meter.
We have to find the width (W) of the rectangle.
We know that,
Perimeter of rectangle is = 2 (L + W)
50 = 2(16 + W)
50 = 32 + 2W
2W = 50 - 32
2W = 18
W = 18/2
W = 9
Hence, The width of the rectangle is 9 meter.
Learn more about Perimeter of rectangle at:
https://brainly.com/question/22109593
#SPJ4
use differentials to estimate the amount of metal in a closed cylindrical can with diameter 10 cm and height 15 cm if the metal is 0.1 cm thick.
Answers
Use differentials to estimate the amount of metal in a closed cylindrical can with diameter 10 cm and height 15 cm if the metal is 0.1 cm thick.Therefore, the estimated amount of metal in the can is 0.001416.
To estimate the amount of metal in a closed cylindrical can with diameter 10 cm and height 15 cm if the metal is 0.1 cm thick, we can use differentials.
First, let's calculate the volume of the can. The volume of a cylinder is calculated by the formula
\(V = πr^{2} h,\)
where r is the radius of the cylinder, and h is its height.
In this case, the radius is 5 cm and the height is 15 cm, so the volume of the can is
\(V = π x (5 cm)^{2} x 15 cm = 707.1 cm^{3}\)
Next, we need to calculate the volume of the metal. The volume of a rectangular prism is
V = l x w x h,
where l is the length, w is the width, and h is the height. In this case, the length and width are both 10 cm, and the height is 0.1 cm, so the volume of the metal is
\(V = 10 cm x 10 cm x 0.1 cm = 1 cm^{3}\)
Finally, we can calculate the amount of metal in the can by dividing the volume of the metal by the volume of the can:
\(1 cm^{3} / 707.1 cm^{3} = 0.001416.\)
for such more question on diameter
https://brainly.com/question/390660
#SPJ11
Which statement about conduction is true?
1.Conduction uses electromagnetic waves.
2.Conduction transfers energy from one particle to another.
3.Conduction produces currents in a heated pot of water.
Answers
Answer:
statement 2, conduction is the transfer of heat through direct contact
In the diagram, AB is 6 units, BC is 30 units, and AE is 4 units. Triangle A C D is shown. Line segment B E is drawn from side C A to side D A to form triangle A B E. The length of C B is 30, the length of B A is 6, and the length of A E is 4. If by the SAS similarity theorem, what is AD?
Answers
Answer:
The length of line AD is 24 units.
Step-by-step explanation:
Got it right on edge2020. :)
Answer:
24
Step-by-step explanation:
got it right on edge
Sidney bought some treats for her puppy. She bought 5 packs of crunchy treats and 7 bags of soft treats. There were 6 crunchy treats in each pack and 8 soft treats in each bag. How many treats did Sidney buy in all?
Answers
There are 86 treats did Sidney buy in all.
We have to given that;
Sidney bought some treats for her puppy.
And, She bought 5 packs of crunchy treats and 7 bags of soft treats.
Since, There were 6 crunchy treats in each pack and 8 soft treats in each bag.
Hence, Total crunchy treats in 5 packs are,
= 5 x 6
= 30
And, Total soft treats in 7 bags are,
= 8 x 7
= 56
Therefore, Total number of treats did Sidney buy in all is,
⇒ 56 + 30
⇒ 86
Learn more about the addition visit:
https://brainly.com/question/25421984
#SPJ1
Nima used 2/3 cup peanuts, 1/2 cup cashews, 3/4cup pecans, and some raisins in a recipe that makes 2-1/4 cups of tiles mix. How many cups of peanuts are there per cup of trail mix?
Answers
Answer:
x = 8/27 of a cup
Step-by-step explanation:
Math: If f(x) = 2x^2 - 5x - 15, what is f(-3)? *
O
24
42
18
3
Answers
Step-by-step explanation:
1 rst. 2 x2-5x-15 da 18 rest
The ratio of c:d is 1:3. The ratio of d:e is 2:3. What is the ratio of c:d:e?
Answers
The ratio of c:d:e is 1:3:2.
How The answer was obtainedTo find the ratio, you can multiply the first ratio by the second ratio: 1 * 2 = 2 and 3 * 3 = 9, so the ratio becomes 2:9:6, which can be simplified to 1:3:2.
A ratio is a comparison between two values. To calculate a ratio, divide the first value by the second value. For example, if you have three apples and seven bananas, the ratio of apples to bananas would be 3/7.
You can also simplify a ratio by dividing both values by their greatest common divisor. For example, if the ratio of apples to bananas is 6/14, you could simplify it to 3/7.
It's also possible to express a ratio as a fraction, decimal, or percentage. To convert a ratio to a fraction, simply divide the two values. To convert a ratio to a decimal, divide the numerator by the denominator. To convert a ratio to a percentage, multiply the ratio by 100.
Learn more on calculations for ratio here https://brainly.com/question/2328454
#SPJ1
How many times bigger is the value of the digit 6 in 64.53 than the
value of the digit 6 in 0.367?
Answers
Step-by-step explanation:
the value of the digit 6 in 64.53 is 60.
the value of the digit 6 in 0.367 is 0.06 or 6/100.
60 = x × 6/100
6000 = 6x
x = 1000
so, the value of the first 6 is 1000 times bigger than the value of the second 6.
The value of the digit 6 in 64.53 is approximately 10010 times bigger than the value of the digit 6 in 0.367.
To find how many times bigger the value of the digit 6 is in 64.53 compared to 0.367, we need to determine the place value of the digit 6 in each number.
In 64.53:
The first 6 (6 before the decimal point) is in the tens place value, which represents 6 * 10 = 60.
The second 6 (6 after the decimal point) is in the hundredths place value, which represents 6 * (1/100) = 0.06.
So, the value of the digit 6 in 64.53 is 60 + 0.06 = 60.06.
In 0.367:
The 6 (6 after the decimal point) is in the thousandths place value, which represents 6 * (1/1000) = 0.006.
So, the value of the digit 6 in 0.367 is 0.006.
To find how many times bigger the value of the digit 6 is in 64.53 compared to 0.367, divide the value in 64.53 by the value in 0.367:
60.06 / 0.006 ≈ 10010
Therefore, the value of the digit 6 in 64.53 is approximately 10010 times bigger than the value of the digit 6 in 0.367.
To know more about digit:
https://brainly.com/question/30856511
#SPJ2
Method: Forty-eight preschoolers (age range =3 years 6 months to 4 years 5 months; 24 boys, 24 girls) watched a video featuring two female actors seated side by side. On each of four trials, one actor announced her intention to hide a ball under one of four cups; the other agreed, covered her eyes, and turned around to face the back wall. The hider placed a small barrier in front of the cups so that the children could watch as she hid the ball but could not see the particular cup she baited. She announced that she had finished and removed the barrier. Both actors faced the camera throughout the rest of the trial. The children were randomly assigned to three conditions. In the point condition (n=16; mean age =3 years 11 months), the two actors simultaneously pointed to different cups. In the grasp condition ( n=16; mean age =4 years 0 months), they simultaneously grasped the tops of different cups. We used grasping as a comparison gesture because young children understand that it, like pointing, is intentional and object-directed (Woodward, 1999). However, it is not often used communicatively, and so may not be as likely as pointing to lead to the misattribution of knowledge. In the baseline condition ( n=16; mean age =3 years 11 months), the two actors simply sat with their hands in their laps. After the actors gestured (or not), the experimenter paused the video and asked, "Who knows where the ball is?" One actor hid the ball on the first and fourth trials; the other actor did so on the middle two trials. Results: Children in the grasp and baseline conditions selected the actor who hid the ball as the one who knew its location more frequently than would be expected by chance, ts (15)>3.74, ps <.01,ds>0.94; specifically, children in the grasp location selected that actor on 3.13(SD=1.20) of the 4 trials, and children in the baseline condition selected her on 3.25(SD=1.06) of the 4 trials. Children in the point condition performed at chance level, t(15)<1, selecting the hider on just 2.13(SD=1.25) trials. An analysis of variance revealed a significant effect of condition, E(2,45)=4.38,p=.018,η2=.16. Children in the point condition were less likely to select the hider than were children in the grasp or baseline condition (Tukey's honestly significant difference, ps<.05 ); performance did not differ between the latter two conditions. Seeing the two actors point may have led children in the point condition to assume that both were knowledgeable. But it is also possible that these children ignored the test question: Rather than indicating which pointer was knowledgeable, perhaps they reflexively indicated where they would search for the ball, which would also lead to chance performance (Palmquist, Burns, \& Jaswal, 2012; Povinelli \& deBlois, 1992). One reason to doubt this possibility is that the children tended to respond to the test question by pointing to an actor's face rather than one of the cups (72\% vs. 28% of trials). However, to investigate this possibility directly, we conducted a control study with 8 different children (mean age =3 years 9 months, range =3 years 6 months to 4 years 1 month; 5 boys, 3 girls). The procedure was the same as in the point condition, but after the actors pointed, the experimenter asked, "Who hid the ball?" If pointing automatically triggers a search response, even when the test question does not ask children to indicate where they would search, they should select the two pointers equally (as they did in the point condition) when this procedure is followed. In fact, however, the children correctly indicated the hider on 3.89(SD=0.35) of the 4 trials, more often than expected by chance, t(7)=15.00,p<.001,d=7.59. Thus, children do not automatically respond to pointing by
Answers
The study found that preschoolers in the grasp and baseline conditions recognized the actor who hid the ball as the one with knowledge of its location, suggesting that pointing gestures influenced their judgments.
In this study, 48 preschoolers participated, ranging in age from 3 years 6 months to 4 years 5 months, with an equal distribution of 24 boys and 24 girls. The children watched a video featuring two female actors seated side by side.
The actors engaged in a task where they hid a ball under one of four cups, while the other actor covered her eyes and turned around. A small barrier was placed in front of the cups, preventing the children from seeing the specific cup where the ball was hidden.
In the grasp condition, the actors simultaneously grasped the tops of different cups.
The baseline condition served as a comparison, where the actors simply sat with their hands in their laps. After the actors performed the gestures or remained in the baseline condition, the video was paused, and the children were asked, "Who knows where the ball is?"
The results showed that children in the grasp and baseline conditions selected the actor who hid the ball as the one who knew its location more frequently than would be expected by chance.
In contrast, children in the point condition performed at chance level, indicating the hider on just 2.13 out of 4 trials
An analysis of variance revealed a significant effect of condition, suggesting that the pointing gesture influenced the children's judgments.
The possibility that children in the point condition ignored the test question and instead reflexively indicated where they would search for the ball was considered.
The results showed that children correctly indicated the hider more often than expected by chance, indicating that they were not simply responding to the pointing gesture.
Learn more about gestures from the given link:
https://brainly.com/question/18074431
#SPJ11
________ is an entire group under study as specified by the objectives of the research project. Select one: a. Study group b. Population c. Sample d. Census
Answers
Population is an entire group under study as specified by the objectives of the research project.
In research methodology, a population refers to the entire group of individuals or elements that are of interest to the researcher and are under study as specified by the objectives of the research project. It represents the larger group from which a sample is drawn. The population is the target group to which the research findings are intended to be generalized.
When conducting research, it is often impractical or impossible to study an entire population due to constraints such as time, cost, and accessibility. Therefore, researchers typically select a subset of the population called a sample. The sample is a smaller representative group that is selected from the population and is used to draw inferences and make generalizations about the population.
The selection of a sample is based on the principle of randomization and aims to ensure that the sample is representative of the population. By studying the sample, researchers can make statistical inferences about the population as a whole.
In summary, the population refers to the entire group under study, while a sample is a subset of the population that is selected for research purposes. The population is the broader target group of interest, and the sample is used to draw conclusions about the population.
To know more about populations, refer here:
https://brainly.com/question/15889243#
#SPJ11
which statement is true about the system of linear equations graphed in the coordinate plane below
Answers
Answer:
Step-by-step explanation:
The system of equations does not have one solution because the lines will never intersect.
the average number of days construction workers miss per year is 11. the standard deviation is 3.1. the average number of days factory workers miss per year is 10 with a standard deviation of 2.7. which class is more variable in terms of days missed?
Answers
The statistics for factory workers is more erratic and has a greater percentage.
The coefficient of variation is an equation that can be used to measure the dispersion of data points in a data set around the mean. It is possible to make the error of counting simply the standard deviation, as I had done in the past.
CV\(=\frac{\sigma}{\mu} *100\)where mu is the population's mean and sigma represents the population's standard deviation.
Construction workers miss per year is 11.
The standard deviation is 3.1.
Every year, factory workers lose 10 days on average.
The standard deviation of 2.7.
The greatest proportion of CV is thought to be more volatile.
Let's do the math:
Construction workers\(=\frac{\sigma}{\mu} =\frac{3.1}{11}= 0.281*100=28.1\)
Factory workers\(=\frac{\sigma}{\mu}=\frac{2.7}{10}=0.27*100=27\)
Since, the factory workers have a higher percentage, their data is more variable.
For more such questions on coefficient of variation
https://brainly.com/question/15563195
#SPJ4
Marshall spins a prize wheel with 4 segments of equal size, one of which is labeled "winner. "
Let X = the number of spins until Marshall wins a prize.
What is the probability that Marshall wins a prize on his 2nd spin?
Recall: P(X = k) = (1 – p)k–1p
Round to 4 decimal places
Answers
The probability that Marshall wins a prize on his second spin = 0.1875
Consider an event X = the number of spins until Marshall wins a prize.
Given that a prize wheel with 4 segments of equal size, one of which is labeled winner.
So, the sample space n = 4
For given event x, the possible outcomes = 1
Using the formula of probability,
p = x/n
p = 1/4
p = 0.25
So, the probability of success p = 0.25
q = 1 - p
q = 1 - 0.25
q = 0.75
To find the probability that Marshall wins a prize on his 2nd spin.
Using formula, \(P(X = k) = (1 - p)^{k-1}p\)
For k = 2,
\(P(X = 2) = (1 - 0.25)^{2-1}\times 0.25\)
P(X = 2) = 0.75 × 0.25
P(X = 2) = 0.1875
Thus, the required probability is 0.1875
Learn more about the probability here:
https://brainly.com/question/30034780
#SPJ4
suppose that professor degroot has a policy of giving as to the top 10% of student scores on his final, regardless of the actual scores. if the distribution of scores on his final exam turns out to be normal with mean 69 and standard deviation 9, how high does your score have to be to earn an a?
Answers
Your score must be greater than or equal to 81 in order to receive an A grade. The mean value comes out to be 80.52.
Here, we are given that professor Degroot has a policy of giving A grade to the top 10% of student scores on his final.
This means in order to earn an A grade, your score should be in the top 10%.
⇒ Z score should be 0.09
we can look at the z tables to find that this value is at z = 1.28
Now, we know z score is calculated as-
z = (X - μ)/ σ
where X = observed value
μ = sample mean
σ = standard deviation
substituting the given values in the formula we get-
1.28 = (X - 69)/ 9
1.28 × 9 = X - 69
11.52 = X - 69
X = 11.52 + 69
X = 80.52
Thus, your score must be greater than or equal to 81 in order to receive an A grade.
Learn more about z tables here-
https://brainly.com/question/25638875
#SPJ4
A thin wire is bent into the shape of a semicircle x2+y2=64,x>=0. If the linear density is a constant k, find the mass and center of mass of the wire.
mass = _____
center of mass (¯x,¯y)(x¯,y¯) = ( _____ )
Answers
The center of mass of the wire is (64/15, 0). To find the mass of the wire, we need to calculate its length first.
Since the wire is bent into the shape of a semicircle, its length is half the circumference of a circle with radius 8 units (since x>=0). Therefore, the length of the wire is πr = π(8) = 8π.
The linear density of the wire is given as k, which means that its mass per unit length is k. Thus, the mass of the wire is the product of its length and linear density: mass = k(8π) = 8kπ.
To find the center of mass, we need to locate the centroid of the semicircle. By symmetry, the centroid lies on the x-axis, and we only need to find its x-coordinate.
The x-coordinate of the centroid can be found using the formula:
x¯ = (1/M) ∫(x dM)
where M is the mass of the wire, and the integral is taken over the semicircle.
Using polar coordinates (x = rcosθ, y = rsinθ), we can rewrite the equation of the semicircle as y = (64-x^2)^0.5.
Then, we have:
dM = kds = k(sqrt(1+(dy/dx)^2))dx = k(1+(x^2/(64-x^2)))^(1/2) dx
Integrating from x=0 to x=8, we have:
x¯ = (1/M) ∫(x dM) = (1/8kπ) ∫(x (1+(x^2/(64-x^2)))^(1/2) dx) = 64/15
Therefore, the center of mass of the wire is (64/15, 0).
Learn more about length here:
https://brainly.com/question/32060888
#SPJ11
ryan rides his bike for 30 minutes and travels a distance of 4 miles. how fast was he traveling? 4 miles per hour 6 miles per hour 8 miles per hour none of these choices are correct.
Answers
Ryan rides his bike for 30 minutes and travels a distance of 4 miles. He was traveling 8 miles per hours.
Ryan rides his bike for 30 minutes and travels a distance of 4 miles.
We have to determine how fast he was traveling.
Time = 30 minutes
First we convert the minutes in hours.
As we know that;
1 hour = 60 minutes.
So 1 minute = 1/60 hours
30 minutes = 30/60 hours
30 minutes = 1/2 hours
Distance = 4 miles
The formula of speed is;
Speed = Distance/Time
Speed = 4/(1/2) miles per hours
Speed = 4 × 2 miles per hours
Speed = 8 miles per hours
To learn more about formula of speed link is here
brainly.com/question/3004254
#SPJ4
the best source for numerical data about life in the united states is
Answers
The best source for numerical data about life in the United States is the U.S. Census Bureau. The Census Bureau is responsible for collecting and analyzing data related to various aspects of life in the country, including population, economy, and demographics.
Firstly, the United States Census Bureau is a reliable source for various types of demographic and economic data. They conduct a national census every ten years and also provide regular surveys and reports on population, housing, employment, and other relevant topics. Another source for statistical data is the Bureau of Labor Statistics, which collects and publishes information on employment, wages, productivity, and other labor-related metrics.
The Census Bureau conducts surveys and gathers data every ten years through the decennial census, as well as through other sources such as the American Community Survey and the Current Population Survey. This information provides valuable insights for policymakers, researchers, and the general public. Their comprehensive data sets cover a wide range of topics and are frequently updated to reflect changes in the country's population and demographics.
To know more about demographics visit:-
https://brainly.com/question/13146758
#SPJ11
Find the x-intercept and the y-intercept.
3x-2y=6
Show work to get Brainliest
Answers
Answer:
There are several different ways to get the x-intercept and y-intercept of an equation. The way that I usually do it is setting one of the variables to zero and finding what the other variable is equal to. For example, if we set x to 0 that means that we are finding the y-intercept as the value of x is 0 which is the y-axis. This is also how it works when setting y to 0. First lets find the x intercept by setting y to 0.
\(3x - 2y = 6\)
\(3x - 2(0) = 6\)
\(\frac{3x}{3} = \frac{6}{3}\)
\(x = 2\)
We now know that the x-intercept is 2 and now we need to determine what the y-intercept is. Now we can just set the x to 0 and find the y-intercept.
\(3x - 2y = 6\)
\(3(0) - 2y = 6\)
\(\frac{-2y}{-2} = \frac{6}{-2}\)
\(y =- 3\)
Therefore, we know that our x-intercept is (2, 0) and our y-intercept is (0, -3) because the first spot in the coordinate pair is the x-value and the second one is the y-value.
Hope this helps
13. The company you work for has downsized and you have lost your job. You receive a severance package of $65 000 and decide to invest it for retirement, earning an average of 7% per year. It has been suggested that you should be able to retire comfortably with $500 000 in savings. If your investment can be modelled with the equation y = 65000(1.07)^x how many years will pass before you reach $500 000?
Answers
Answer:
31 years
Step-by-step explanation:
65000*(1.07) ^31 is around $529000
however, 65000*(1.07) ^30 is around $491000
so you would need 31 years to gain more than $500,000.
It will take approximately 30 years to reach $500,000 in savings with an investment that earns an average of 7% per year.
To determine the number of years it will take to reach $500,000 in savings with an investment that earns an average of 7% per year, we can use the given investment model equation: y = 65000(1.07)ˣ.
We need to find the value of x, which represents the number of years.
Setting y = $500,000, we can solve for x:
500,000 = 65,000(1.07)ˣ
500,000/65,000 = (1.07)ˣ
100/13 = (1.07)ˣ
To solve for x, we take the logarithm of both sides:
ln 100/13 = ln (1.07)ˣ
ln 100/13 = x ln (1.07)
x = (ln 100/13)/(ln (1.07))
x = 30
Therefore, it will take approximately 30 years to reach $500,000 in savings with an investment that earns an average of 7% per year.
Learn more about exponential function here:
brainly.com/question/11487261
#SPJ4
SL and SK are tangent to the circle find x
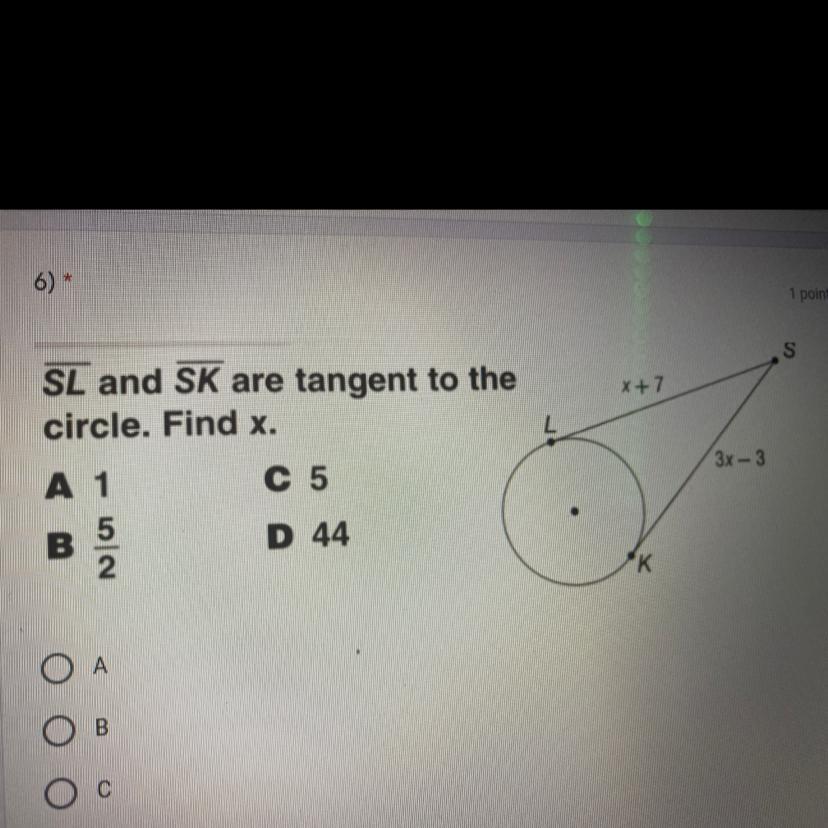
Answers
Answer:
B. 5/2
Step-by-step explanation:
ABC and XYZ are similar triangles with right angles at B and Y. AC=13 cm,
BC=5 cm. Find AB and XZ. (No links pls...)
Answers
Answer:
See belowStep-by-step explanation:
Since B is the right angle, AC is the opposite side - hypotenuse.
Use Pythagorean and find the missing side, AB:
\(AB = \sqrt{AC^2-BC^2} = \sqrt{13^2-5^2} =\sqrt{144} =12cm\)There is no info given to link the triangles ABC and XYZ and hence can't provide solution to any dimension of XYZ.
If the scale factor was given as k, then XZ would be:
XZ = k*BC = 5khola alguien habla español parece que en esta region hablan ingles
Answers
Answer:
yo si apenas me lo descargue
6. The quadratic functions f(x)=-x² + 2x+6 and g(x)=x² + 2x are shown graphed below. The positive
solution to f(x) = g(x) is closest to which of the following?
(1) x = 6.5
(3) x=1.7
(2) x = 3.7
(4) x=0.5
Answers
What is the value of 19 cubed? A: 22 B: 57 C: 361 D: 6,859
Answers
Hope this helps :)
Answer = D. 6,859
The value of 19 cubes is equal to 6859. The correct option is D.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that the number is 19. The cube of 19 will be calculated as:-
19³ = 19 x 19 x 19
19³ = 6859
The cube of 19 is calculated by multiplying the number three times. Hence, the cube of 19 is 6859.
To know more about an expression follow
https://brainly.com/question/1615668
#SPJ2
a farmer plans to enclose a rectangular pasture adjacent to a river (see figure). the pasture must contain 245,000 square meters in order to provide enough grass for the herd. no fencing is needed along the river. what dimensions will require the least amount of fencing?
Answers
X = 700 m and Y = 350 m will require the least amount of fencing.
Area of a rectangular field = length × breath = 245000 = XY
⇒ Y = 245000/X
Perimeter of a rectangular field = X + 2Y
⇒P = X+ 2Y
⇒P = X + 490000/X
⇒ X + 490000X⁻¹
⇒P [X] = X + 490000X⁻¹
⇒P'[X] = 1+[-490000X⁻²]
⇒0 = 1 - 490000/X²
⇒X²= 490000
⇒X = 700 unit
As XY = 245000 [ area of a rectangle ]
⇒700Y = 245000
⇒Y = 350 unit.
Hence , P is minimum [ fencing ] when X = 700 unit and Y = 350 unit.
To understand more about maxima and minima refer -
https://brainly.com/question/27958412
#SPJ4
Which weighs more: a watermelon that weighs 7.5 kilograms or a baby that weighs 12 pounds? Explain your reasoning. Note: 1 pound is about 0.45 kilograms.
Answers
Answer: The watermelon weighs more than the baby.
Step-by-step explanation:
I think that the watermelon that weighs 7.5 kilograms is more than a baby because 1 pound is 0.45 kilograms. So that means that 7.5 kilograms is 16.53 pounds which weighs more than 12 pounds.
The watermelon weight is more than baby weight.
What is Measurement unit?
A measurement unit is a standard quality used to express a physical quantity. Also it refers to the comparison between the unknown quantity with the known quantity.
Given that;
A watermelon weighs = 7.5 kilograms
And, A baby weighs = 12 pounds
Now,
Since, 1 kg = 2.2 pounds
Hence, The watermelon weight = 7.5 x 2.2 pounds
= 16.5 pounds
Thus, The watermelon weight is more than baby weight.
Learn more about the measurement unit visit:
https://brainly.com/question/777464
#SPJ2
Find the solution set for this inequality, -2x + 4 > -4x + 8
Answers
Answer:
The answer is
x > 2Step-by-step explanation:
- 2x + 4 > - 4x + 8
Add 4x to both sides of the inequality
That's
- 2x + 4x + 4 > - 4x + 4x + 8
2x + 4 > 8
Subtract 4 from both sides
That's
2x + 4 - 4 > 8 - 4
2x > 4
Divide both sides by 2
That's
\( \frac{2x}{2} > \frac{4}{2} \)
We have the final answer as
x > 2Hope this helps you
Can someone help me with questions 5&6 please

Answers
Answer:
5) B. -6
6) A. 2/3
Step-by-step explanation:
take two points (3, 2) and (12, 8) and use the equation y2- y1 / x2 - x1 to find the slope
(8-2) / (12-3)
6/9 simplified to 2/3