Alice gave Bob as many dollars as Bob had. Bob then gave Alice as many dollars Alice then had. At this point, each had 24 dollars. How much did Alice have at the beginning?
Please answer it step-by-step, and explained it very detailed. Thx.
Answers
Answer:
Alice started with $30
Step-by-step explanation:
Understanding the situation
There are 3 steps to the transactions:
the initial amounts, (before any transfers)the amounts after Alice first gives Bob money, andthe amounts after Bob gives Alice some money back.Organizing the variables
For organizational purposes, let's create variables for each person for each stage of the transaction, variables "a" for Alice, and "b" for Bob, with subscripts to denote which stage of the process we're talking about. For instance, \(a_1\) is the amount Alice has at step 1 (before any transfers), and \(b_3\) is the amount Bob has after Bob gives Alice some money back at the end.
Translating the sentences into equations
"Alice gave Bob as many dollars as Bob had."
This means that the magnitude of the change for Alice between her Step 1 and Step 2 was equal to the amount Bob had at the beginning (Step 1): \(a_1-a_2=b_1\)
This also means that Bob's money in Step 2 increased to double what it used to be in Step 1: \(b_2=2b_1\)
"Bob then gave Alice as many dollars Alice then had."
Similar to the last sentence, this means that the magnitude of the change for Bob between Step 2 and Step 3 was equal to the amount Alice had at Step 2: \(b_2-b_3=a_2\)
It also means that Alice's money in Step 3 increased to double what it used to be in Step 2: \(a_3=2a_2\)
"At this point, each had 24 dollars"
This means that both people had 24 dollars at Step 3: \(a_3=24\) and \(b_3=24\)
"How much did Alice have at the beginning?"
Solve for \(a_1\)
Solving the system of equations
We effectively have a system of 6 equations and 6 unknowns. To solve this system, we'll be using substitution. For ease of explanation, I'll number the equations below:
Eq1: \(a_1-a_2=b_1\)
Eq2: \(b_2=2b_1\)
Eq3: \(b_2-b_3=a_2\)
Eq4: \(a_3=2a_2\)
Eq5: \(a_3=24\)
Eq6: \(b_3=24\)
Substitute Eq6 (\(b_3=24\)) into Eq4
Eq4: \(a_3=2a_2\)
\((24)=2a_2\)
divide by 2
\(12=a_2\) ***(we'll need this later)
Substitute this (\(12=a_2\)) and Eq5 (\(a_3=24\)) into Eq3
Eq3: \(b_2-b_3=a_2\)
\(b_2-(24)=(12)\)
add 24
\(b_2=36\)
Substitute this (\(b_2=36\)) into Eq2
Eq2: \(b_2=2b_1\)
\((36)=2b_1\)
Divide by 2
\(18=b_1\)
Substitute this (\(18=b_1\)) and ***(\(12=a_2\)) into Eq1:
Eq1: \(a_1-a_2=b_1\)
\(a_1-(12)=(18)\)
Add 12
\(a_1=30\)
So, Alice had 30 dollars at Step 1, before she gave any to Bob.
Related Questions
so, i' m doing my homework and i came across this question and i was confused...so can u please help me out, the person that gives me the MOST DESCRIBED answer will get Brainliest!! <3

Answers
Answer:
20 22 28 32 33 65 159
median =32
mean= 51.285714285
What is the angle relationships

Answers
acceptance sampling, a sample of items is randomly selected without replacement and the entire batch is accepted if every item in the sample is okay. the abc electronics company has just manufactured 2100 write-rewrite cds, and 50 are defective. if 3 of these cds are randomly selected for testing, what is the probability that the entire batch will be accepted?
Answers
The probability that the entire batch will be accepted will be 9339
4000-90 = 3910 (non-defective) (non-defective)
If P(first not defective) = 3910/4000 and it is not changed (1 less to choose from and 1 less not defective)
P(second is not flawed if first is flawed) = 3909/3999 If the item is also not replaced (a total of 2 less to choose from and 2 less not defective)
P
(1st and 2nd are not defective, so the third is also not defective)) = 3908/3998
Simply multiply these three fractions to get the answer: 3910(3909>)(3908)) / (4000(3999)(3998)).
=9339
Know more about probability
https://brainly.com/question/24756209
#SPJ4
The graph represents revenue in dollars as a function of greeting cards sold.
A coordinate plane showing Greeting Card Revenue, Number of Cards Sold on the x-axis and Revenue in dollars on the y-axis. A line starts at (0. 0) and passes through (2, 8), (4, 16), and ends at (5, 20).
Which equation represents the function shown on the graph?
y = x
y = x
y = 2x
y = 4x
Answers
Answer: The equation that represents the graph is y=4x.
Step-by-step explanation: If you plug in just one coordinate in each equation, you will find that these are the following outcomes no matter which coordinate you pick(but I'm picking (2,8) for your view):
y=x , 8=2
y=x , 8=2
y=2x , 8=4
y=4x , 8=8(ONLY CORRECT STATEMENT)
Answer:
y= 4x
Step-by-step explanation:
Need help really quick look at the picture thank you soooooooo,, muchh

Answers
Answer:
The answer would be -7/12
Step-by-step explanation:
Use math.way itll help you tremendously :)
Write an equation in which the distributive property, commutative property, associative property, addition or subtraction property, and multiplication property can be used to find the solution. Then solve the equation. Justify each step.
Answers
Answer:
There are many times in algebra when you need to simplify an expression. The properties of real numbers provide tools to help you take a complicated expression and simplify it.
The associative, commutative, and distributive properties of algebra are the properties most often used to simplify algebraic expressions. You will want to have a good understanding of these properties to make the problems in algebra easier to work.
Step-by-step explanation:
Commutative Property of Multiplication
For any real numbers a and b, a · b = b · aOrder does not matter as long as the two quantities are being multiplied together. This property works for real numbers and for variables that represent real numbers.
just as subtraction is not commutative, neither is division commutative. 4 ÷ 2 does not have the same quotient as 2 ÷ 4.Associative Property of Addition
For any real numbers a, b, and c, (a + b) + c = a + (b + c).
Associative Property of Multiplication
For any real numbers a, b, and c, (a • b) • c = a • (b • c).Multiplication has an associative property that works exactly the same as the one for addition. The associative property of multiplication states that numbers in a multiplication expression can be regrouped using parentheses. For example, the expression below can be rewritten in two different ways using the associative property.
The parentheses do not affect the product, the product is the same regardless of where the parentheses are.
The distributive property of multiplication is a very useful property that lets you rewrite expressions in which you are multiplying a number by a sum or difference. The property states that the product of a sum or difference, such as 6(5 – 2), is equal to the sum or difference of products, in this case, 6(5) – 6(2).
6(5 – 2) = 6(3) = 18
65) – 6(2) = 30 – 12 = 18
The distributive property of multiplication can be used when you multiply a number by a sum. For example, suppose you want to multiply 3 by the sum of 10 + 2.3(10 + 2) = ?
According to this property, you can add the numbers 10 and 2 first and then multiply by 3, as shown here: 3(10 + 2) = 3(12) = 36. Alternatively, you can first multiply each addend by the 3 (this is called distributing the 3), and then you can add the products. This process is shown here.
3 (10 + 2) = 3(12) = 36
3(10) + 3(2) = 30 + 6 = 36
The products are the same.
since multiplication is commutative, you can use the distributive property regardless of the order of the factors.
What is the measure of angle BOC'?
A) 79 degrees
B) 35 degrees
C) 66 degrees
D) 114 degrees

Answers
If AB = 10 and B lies at -6, where could A be located?
Answers
Answer:
26
Step-by-step explanation:
AB to B is 16 units, so it's reasonable to assume that A to AB is 16 units as well.
The lifespans of gorillas in a particular zoo are normally distributed. The average gorilla lives 20. 820. 820, point, 8 years; the standard deviation is 3. 13. 13, point, 1 years.
Answers
A z-score of 23.9 years must be located in the gorillas' lifespans in a specific zoo's typical normal distribution.
Define the term normal distribution?A data collection with a normal distribution is put up so that the majority of the values cluster as in midpoint of the range and the remaining values taper off symmetrically in either direction.The equation can be used to determine the z score.
z = (x - μ)/σ
In which,
X is age 23.9.The typical gorilla life span is M. (20.8 years).The standard deviation is s. (3.1 years).Then,
z = (23.9 - 20.8)/3.1
z = 1
According to the empirical rule, 68% of lifespans are within one standard deviation of the mean.
Half of it, 68/2 = 34% %, is on the right side of the mean's standard deviation.
Given that the likelihood of a gorilla lasting less than 23.9 years is 50%.
A gorilla's lifespan being less than the norm means is;
50% + 34% = 84% sits below z-score 1.
Thus, the probability of a gorilla living less than 23.9 years is 84%.
To know more about the normal distribution, here
https://brainly.com/question/23418254
#SPJ4
The correct question is-
The lifespans of gorillas in a particular zoo are normally distributed. The average gorilla lives 20.8 years; the
standard deviation is 3.1 years.
Use the empirical rule (68 – 95 - 99.7%) to estimate the probability of a gorilla living less than 23.9 years.
The museum of natural history has an auditorium that can seat 200 people. A class of 45 students is seated in the auditorium for a lecture. What decimal represents the portion of the seats in the auditorium that are empty ?
Answers
Answer: 1.55
Step-by-step explanation:70 percent sure, might be .155
What is 5n = 185 what’s the n=__?
249 = 3y y=__?
-6w = 354 w=__?
Answers
1. n = 37
isolate n by dividing both sides by 5
2. y = 83
isolate y by dividing both sides by 3
3. w = -118
isolate w by dividing both sides by -6
Which choice shows a true conditional, with the hypothesis and conclusion identified correctly?
A:
If two lines intersect at right angles, then the two lines are perpendicular.
Hypothesis: Two lines are perpendicular.
Conclusion: Two lines intersect at right angles.
B:
If two lines intersect at right angles, then the two lines are perpendicular.
Hypothesis: Two lines are perpendicular.
Conclusion: Two lines do not intersect at right angles.
C:
Two lines are parallel if the lines intersect at right angles.
Hypothesis: Two lines intersect at right angles.
Conclusion: Two lines are parallel.
D:
Two lines are perpendicular if the lines intersect at right angles.
Hypothesis: Two lines intersect at right angles.
Conclusion: Two lines are perpendicular.
Answers
Answer:A:
If two lines intersect at right angles, then the two lines are perpendicular.
Hypothesis: Two lines are perpendicular.
Conclusion: Two lines intersect at right angles.
Step-by-step explanation:
The length of the hypotenuse of a right triangle is 7 feet, and the length of one leg is 4 feet. what is the length of the other leg to the nearest tenth of a foot
Answers
The length of the other leg to the nearest tenth of a foot is 5.7 feet.
What is Pythagorean theorem?
A theorem in geometry: the square of the length of the hypotenuse of a right triangle equals the sum of the squares of the lengths of the other two sides.The Pythagoras theorem equation is expressed as, \(c^{2} = a^{2} + b^{2}\), where 'c' = hypotenuse of the right triangle and 'a' and 'b' are the other two legs.We can use the Pythagorean Theorem to find the length of the other leg
\(a^{2} + b^{2} = c^{2}\)
"a" and "c" represent the two legs of the triangle and "b" represents the perpendicular.
So,
\(b^{2} = c^{2} - a^{2}\)
= 7² - 4²
b = \(\sqrt{49 - 16}\)
\(b = \sqrt{33}\) ⇒ 5.7 feet
Therefore, the length of the other leg to the nearest tenth of a foot is 5.7 feet.
Learn more about Pythagorean Theorem brainly.com/question/14605061
#SPJ4
In BMX racing, racers purchase a one year membership to a track. They also pay an entry fee for each
race at that track. One racer paid a total of $125 after 5 races. Another rider paid a total of $170 after 8
races. Write a function, f(x) that represents the total fees paid for x races
Answers
dont know anyway answer my question i have an f in math and my mom will take my phone.
Which of these equations represents a line parallel to the line 2x + y = 6?
A) y= 2X+3
B) y -2X=4
C) 2X -y=8
D) y= -2X+1
Answers
Answer:
D) y= -2X+1
Step-by-step explanation:
All of the lines are perpendicular to the line 2x+y=6 except for D) y= -2X+1.
in how many ways can a committee of 20 members choose a president, a vice-president, and a secretary?
Answers
There are 6840 ways to choose a president, a vice-president, and a secretary from a committee of 20 members.
To choose a president, a vice-president, and a secretary from a committee of 20 members,
We will use the formula for combinations,
which is: C(n, k) = n! / (k! (n - k)!)
where n is the total number of members and k is the number of members being chosen.
So, for n = 20 and k = 1, we have:
C(20, 1) = 20! / (1! (20 - 1)!) = 20
This gives us 20 choices for the president.
For the vice president,
We need to choose 1 member from the remaining 19 members.
So, for n = 19 and k = 1,
we have:
C(19, 1) = 19! / (1! (19 - 1)!) = 19
This gives us 19 choices for the vice president.
Finally, for the secretary,
We need to choose 1 member from the remaining 18 members.
So, for n = 18 and k = 1,
we have:
C(18, 1) = 18! / (1! (18 - 1)!) = 18
This gives us 18 choices for the secretary.
Now for finding the total number of ways to choose the three positions, we multiply the number of choices for each position:
So, the required number of ways will be 20 * 19 * 18 = 6840
For more questions on Permutation and Combination
https://brainly.com/question/30366889
#SPJ4
An airline claims that it rarely loses a passenger's checked luggage, and, if checked luggage is lost, 90% of the luggage is recovered and returned to the owner within 24 hours. A consumer group believes the 24-hour recovery rate of lost luggage is actually lower (worse) than the airline's claim. They surveyed a large random sample of the airline's customers and found that 103 of 122 people who had lost luggage were reunited with the missing items within 24 hours. Is this enough evidence to claim the proportion of people who lost luggage with this airline a
Answers
The number that corresponds to the null hypothesis and the alternative hypothesis will be 3 and 6 respectively.
What is a null hypothesis?Specify the correct number from the list below that corresponds to the appropriate null and alternative hypotheses for this problem.
It should be noted that the null hypothesis suggests that there's no statistical relationship between the variables.
The alternative hypothesis is different from the null hypothesis as it's the statement that the researcher is testing.
In this case, the number that corresponds to the null hypothesis and the alternative hypothesis will be 3 and 6 respectively.
Learn more about hypothesis on:
brainly.com/question/15980493
#SPJ12
Suppose that A and B are events with P(A) = 0.5, P(B) = 0.1, and P(A and B) = 0.3. What is the probability that B will occur, if A occurs? Question 3 1 pts Suppose that A and B are events with P(A) = 0.3 and P(B) = 0.4. Furthermore, if A happens, then B must also happen. What is P(A or B)? O 0.3 O 0.4 O 0.58 O 0.7 O Not enough information given Question 4 1 pts Suppose that A and B are mutually exclusive, that P(A) = 0.7, and that P(B) = 0.2. Which of the following is true? O P(B|A) > P(B) O P(BIA) = P(B) O P(BIA) < P(B)
Answers
A and B are mutually exclusive, with P(A) is 0.7 and P(B) is 0.2, the probability of event B given event A (P(B|A)) and the probability of event B given event A (P(BIA)) are both 0.2.
To find the probability of B given A, we can use the formula:
P(B|A) = P(A and B) / P(A)
Given:
P(A) = 0.5
P(B) = 0.1
P(A and B) = 0.3
P(B|A) = 0.3 / 0.5
= 0.6
Therefore, the probability that B will occur if A occurs is 0.6.
Given:
P(A) = 0.3
P(B) = 0.4
Since A happening guarantees that B must also happen, the events A and B are not independent. In this case, we can use the formula:
P(A or B) = P(A) + P(B) - P(A and B)
P(A or B) = 0.3 + 0.4 - 0.3
= 0.4
Therefore, the probability of A or B occurring is 0.4.
Given:
P(A) = 0.7
P(B) = 0.2
Since A and B are mutually exclusive events, they cannot occur together. In this case, we have:
P(A and B) = 0
Therefore, P(B|A) = P(BIA)
= 0.
P(BIA) = P(B)
= 0.2.
So, P(BIA) < P(B) is true.
When events A and B are mutually exclusive, with P(A) = 0.7 and P(B)
= 0.2, the probability of event B given event A (P(B|A)) and the probability of event B given event A (P(BIA)) are both 0.2.
To know more about probability, visit:
https://brainly.com/question/23417919
#SPJ11
10. The sum of the measures of the angles of a triangle is 180°.
Write and solve an equation to find the missing measure.
35°
45
Answers
Answer:
180 - 35 - 45= 100
Step-by-step explanation:
100 is the missing measureI need help with these question my teacher doesnt explains that well
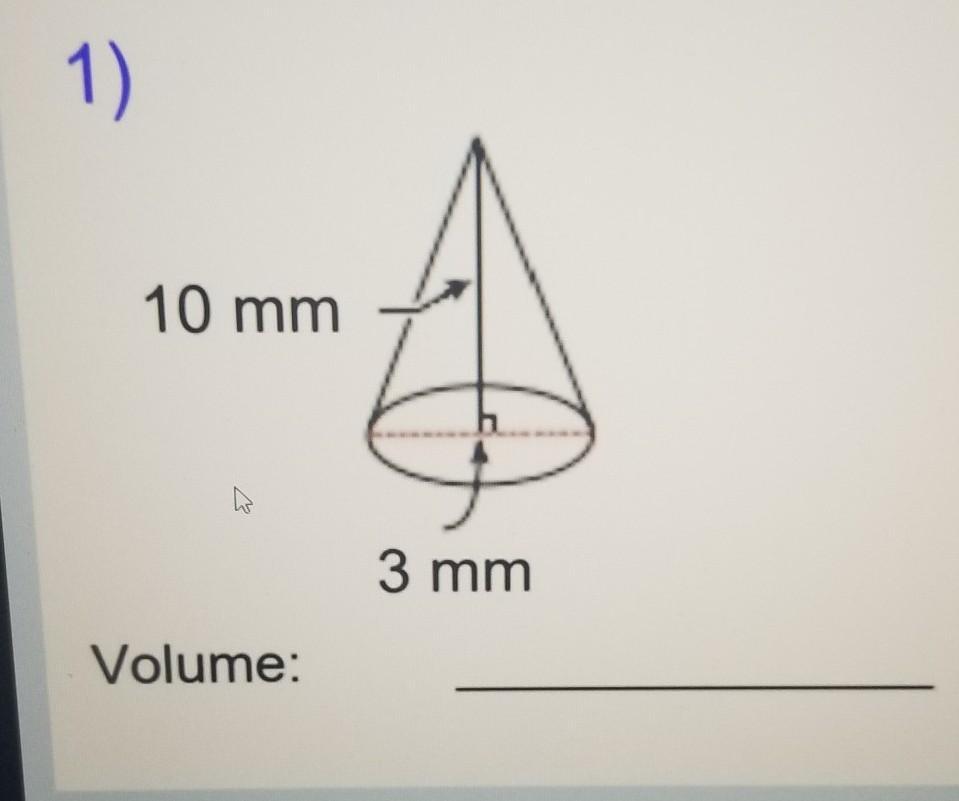
Answers
the formulam of the volume is
\(V=\frac{\pi\times r^2\times h}{3}\)where r is the radius and h the height
r=3/5 because is the half of diameter
h=10
so replacing
\(\begin{gathered} V=\frac{\pi\times(\frac{3}{5})^2\times10}{3} \\ \\ V=\frac{\pi\times\frac{9}{25}\times10}{3} \\ \\ V=\frac{6}{5}\pi\approx3.78 \end{gathered}\)the volume of the cone is 3.78 square millimeters
\(\frac{\frac{9}{25}\times10}{3}=\frac{\frac{90}{25}}{\frac{3}{1}}\)the red multiplication is the numerator and green the denomintor
\(\frac{90\times1}{25\times3}=\frac{90}{75}\)simplify by 15
\(\frac{\frac{90}{15}}{\frac{75}{15}}=\frac{6}{5}\)and then add the pi

Ex2. Prime Numbers ( 40 points) You will implement in this exercise an ancient Greek algorithm for finding the prime numbers less than a given number. (ask your instructor about the name of the algorithm after class!) Reminder: A prime number is a positive integer greater than 1 that is divisible only by itself and by 1 . Here is how the algorithm works assuming we would like to find the prime numbers ≪=20 : 1. Initially, assume that all the numbers are prime by marking them with 1 (0 means not prime). 2. For each number that is marked as prime, starting at 2, mark all of its multiples as not prime. which marks all the multiples of num in the array (of size n ) as not prime (excluding num). 2. Write a program that prints the prime numbers κ=150 : a) Create and initialize an array for marking the numbers with 0 (not prime) or 1 (prime). b) For every number 2<=i<150, use function cross_multiples_out to mark all of its multiples as not prime. c) Pass through the array and print the numbers marked as prime.
Previous question
Answers
The code efficiently identifies prime numbers using the ancient Greek algorithm. It initializes an array, marks the multiples of each prime number as non-prime, and then prints the prime numbers.
This algorithm demonstrates a straightforward and efficient method for finding prime numbers within a given range.The ancient Greek algorithm for finding prime numbers less than or equal to a given number is implemented in the provided Python code. The algorithm follows a simple approach of marking numbers as prime or non-prime.
It starts by assuming all numbers as prime and then proceeds to mark the multiples of each prime number as non-prime. The code initializes an array where each element represents a number and marks them all as prime initially. Then, it iterates over each number from 2 to the given number, checking if it is marked as prime. If it is, the algorithm crosses out all its multiples as non-prime. Finally, it prints the numbers that remain marked as prime.
Learn more about prime here: https://brainly.com/question/9315685
#SPJ11
BRAINLIEST ANSWER!! REALLY EASY JUST NEED TO SHOW YOUR WORK!
-2x-10x+12=18
Answers
Answer:
x= -2.5
Step-by-step explanation:
Combine like terms, add 12 to both sides, then divide by the coefficient.
-2x-10x+12= 18
-12x+12=18
-12x=30
x=-2.5
For the following set of data:
x y 2 1 7 10 5 8 3 0 3 4 4 13
find the regression equation for predicting y from x.
Answers
The regression equation for predicting y from x in the given set of data is y = 1.909x + 2.227. This equation represents the line of best fit that minimizes the sum of squared residuals between the predicted values and the actual values of y based on the corresponding values of x.
To find the regression equation, we use the method of least squares to fit a line to the data points. The equation takes the form of y = mx + b, where m is the slope (coefficient of x) and b is the y-intercept. Using the given set of data, we calculate the slope (m) and the y-intercept (b) to determine the regression equation.
By applying the formulas for m and b:
m = (nΣxy - ΣxΣy) / (nΣx² - (Σx)²)
b = (Σy - mΣx) / n
where n is the number of data points, Σxy is the sum of the products of x and y, Σx and Σy are the sums of x and y respectively, and Σx² is the sum of the squares of x.
By substituting the values from the given data set into these formulas, we obtain the values for m and b. The resulting regression equation for predicting y from x in this case is y = 1.909x + 2.227. This equation represents the line that best fits the data points and can be used to estimate or predict the value of y for any given x within the range of the data.
To know more about regression refer here:
https://brainly.com/question/31969332
#SPJ11
below. The bowl is a cylinder with a depth
of 10 cm. If the bowl has a diameter of
30 cm, what is the exposed surface area
of the birdbath, including the pillar and
pedestal?

Answers
The total exposed surface area of the birdbath, including the pillar and pedestal, is therefore 942 cm² + 300 cm² + 600 cm² = 1842 cm².
What is surface area?Surface area is a two-dimensional measure that refers to the total area of a surface, such as the area of a two-dimensional shape, a three-dimensional solid, or a combination of both. It is the sum of the areas of all the faces of a solid object. It is also referred to as the area of the boundary of a three-dimensional object. It can be used to calculate the volume of an object, and is also used in other calculations like area of the base of a triangle, area of a circle, and more.
The exposed surface area of the birdbath including the pillar and pedestal can be determined by calculating the surface area of the cylinder and adding the surface area of the pillar and pedestal.
The formula for the surface area of a cylinder is 2πr² + 2πrh, where r is the radius of the cylinder and h is the height. In this case, the radius of the birdbath is 15 cm (half of the diameter of 30 cm) and the height is 10 cm. Therefore, the surface area of the cylinder is 2π(15 cm)² + 2π(15 cm)(10 cm) = 942 cm².
The surface area of the pillar and pedestal can be calculated by multiplying the height and circumference of each. The height of the pillar is 10 cm and the circumference is 30 cm, so the surface area of the pillar is 300 cm². The height of the pedestal is 20 cm and the circumference is 30 cm, so the surface area of the pedestal is 600 cm².
The total exposed surface area of the birdbath, including the pillar and pedestal, is therefore 942 cm² + 300 cm² + 600 cm² = 1842 cm².
To know more about surface area click-
https://brainly.com/question/1297098
#SPJ1
This triangle has one side that lies on an extended line segment.
Based on this triangle, what statement about x is true?
x = 33 because 180−147=33
x = 62 because 147−85=62 and 85 + 62 = 147
x = 95 because 180−85=95 and 85 + 95 = 180
x = 118 because 180 − 147 + 85 = 33 + 85 = 118
Answers
The measure of angle x is 80 degrees, which is statement (4) x = 118 because 180 − 147 + 85 = 33 + 85 = 118.
Based on the given information, statement (4) x = 118 because 180 − 147 + 85 = 33 + 85 = 118 is true.
In a triangle, the measures of the three angles add up to 180 degrees. In this triangle, one of the angles measures 85 degrees, and another angle measures 147 degrees. Therefore, the measure of the third angle must be 180 - 85 - 147 = 48 degrees.
Since the measure of the third angle is 48 degrees, and the measure of one of the other angles is 33 degrees, the measure of the remaining angle must be 48 - 33 = 15 degrees.
Finally, since the measure of one angle is 85 degrees and another angle is 15 degrees, the measure of the third angle must be 180 - 85 - 15 = 80 degrees.
Therefore, the measure of angle x is 80 degrees, which is statement (4) x = 118 because 180 − 147 + 85 = 33 + 85 = 118.
To learn more about the triangle, visit:
brainly.com/question/2773823
#SPJ4
e0.02t
where
The population of a town is modeled by the equation P = 16, 581e'
Prepresents the population tyears after 2000. According to the model, what
will the population of the town be in 2020?
CL
Answers
g what is the root-mean-square speed (urms) of a co2 molecule that has an average ke of 5.44 x 10-21 j/molecule?
Answers
The root mean square speed of a carbon dioxide molecule at mentioned average kinetic energy is 1.57× \( {10}^{-11} \).
The formula to find root mean square speed of carbon dioxide molecule using average kinetic energy is as follows -
c = ✓2KE/m, where c is root mean square speed, KE is kinetic energy and m is molecular mass
Keep the values in formula to find the root mean square speed.
c = ✓2×5.44×\( {10}^{-21} \)/44
Performing multiplication and division on Right Hand Side of the equation
c = ✓2.47×\( {10}^{-22} \)
Taking square root on Right Hand Side of the equation
c = 1.57× \( {10}^{-11} \)
Learn more about root mean square speed
https://brainly.com/question/25959744
#SPJ4
K
Solve the system of equations by substitution.
2x + y = 6
y = 4x
Points: 0 of 1
Save
Select the correct choice below and, if necessary,
fill in the answer box to complete your choice.
OA.
There are a finite number of solutions. The
solution set is
(Simplify your answer. Type an
ordered pair.)
B. There are infinitely many solutions. The
solution set is {(x)}.
(Simplify your answer. Type an expression
in terms of x.)
OC. The solution set is Ø.
Answers
Answer:
The solution set is (1, 4)
There are a finite number of solutions.
Step-by-step explanation:
We have 2x+y=6 and y=4x.
Let's write the first equation into y=mx+b form.
We get: y=-2x+6
Now, we just set the equations equal to each other.
-2x+6=4x Add 2x to both sides.
6=6x Divide both sides by 6
x=1
Now, plug x back into either of the equations given to us.
y=4(1)
y=4
The solution set is (1, 4)
2x + 4x = 6
Simplifying, we get:
6x = 6
Dividing by 6, we get:
x = 1
Substituting x = 1 into y = 4x, we get:
y = 4(1)
y = 4
So, the solution is (1, 4), and there is a unique solution to the system of equations.
The answer is OA. The solution set is (1, 4).
The r.v. X is distributed as uniform distribution over (−αα), where α>0 > 0. Determine the parameter α
so that each of the following equalities holds:
a. P(-1 < X < 2) = 0.75
b. P(|X| < 1) = P(|X| > 2)
Answers
a. There are no real solutions to the equation. Therefore, there is no value of α for which P(-1 < X < 2) = 0.75.
b. The value of parameter α for P(|X| < 1) = P(|X| > 2) is 4
a. We know that for a uniform distribution over (−α,α), the probability density function is given by f(x) = 1/(2α) for −α ≤ x ≤ α and zero otherwise. Thus, the probability of the event (-1 < X < 2) can be computed as:
P(-1 < X < 2) = ∫(-1)²/(2α) dx + ∫2²/(2α) dx
= (1/2α) ∫(-1)² dx + (1/2α) ∫2² dx
= (1/2α) [x]₋₁¹ + (1/2α) [x]²₂
= (1/2α) (2α - 1) + (1/2α) (4 - α²)
= (3 + α²)/(4α)
We want this probability to be 0.75. So, we solve the equation (3 + α²)/(4α) = 0.75 for α:
(3 + α²)/(4α) = 0.75
=> 3 + α² = 3α
=> α² - 3α + 3 = 0
This is a quadratic equation in α with discriminant:
Δ = b² - 4ac
= (-3)² - 4(1)(3)
= 9 - 12
= -3
Since Δ is negative, there are no real solutions to the equation. Therefore, there is no value of α for which P(-1 < X < 2) = 0.75.
b. The pdf of a uniform distribution is given by:
f(x) = 1/(b-a), for a ≤ x ≤ b
In this case, a = -α and b = α. Therefore,
f(x) = 1/(2α), for -α ≤ x ≤ α
Now we can calculate the probabilities as follows:
P(|X| < 1) = P(-1 < X < 1) = ∫(-1 to 1) f(x) dx = ∫(-1 to 1) 1/(2α) dx = 1/(2α) * [x]_(-1 to 1) = 1/α
P(|X| > 2) = P(X < -2 or X > 2) = P(X > 2) + P(X < -2) = ∫(2 to α) f(x) dx + ∫(-α to -2) f(x) dx = ∫(2 to α) 1/(2α) dx + ∫(-α to -2) 1/(2α) dx = 1/4
Therefore, we need to find α such that P(|X| < 1) = P(|X| > 2) = 1/4.
From P(|X| < 1) = 1/α, we get α = 1/P(|X| < 1) = 1/(1/4) = 4.
From P(|X| > 2) = 1/4, we get the same value of α = 4.
Hence, α = 4 satisfies both conditions.
Learn more about uniform distribution at https://brainly.com/question/15171449
#SPJ11
3(2x − 8) – 11x
equivalent to
Answers
Answer:
-5x - 24
Step-by-step explanation:
3(2x − 8) – 11x =
Distribute the 3.
= 6x - 24 - 11x
Combine like terms.
= -5x - 24