An accountant needs to withhold 15% of income for taxes if the income is below $40,000, and 23% of income if the income is $40,000 or more. The income amount is in cell A1. Write a spreadsheet expression that would calculate the amount to withhold.
Answers
Answer:
=if(A1<40000,.15*A1,if(A1
Step-by-step explanation:
>=4000,.23*A1))
Related Questions
A zookeeper predicted that the weight of a newborn lion would be 2.8
pounds.When the zoo's lion gave birth, the newborn weighed 3.5 pounds.
Which proportion shows how to find the zookeeper's percent error?
Answers
Answer:
sorry i dunno the answer hope you have a great day
Step-by-step explanation:
Help with Geometry, find X.

Answers
Answer:
541.9
Step-by-step explanation:
Should be, don’t trust me 100%
Ramon invested a total $9,700 into two accounts, account 1 earns 6% simple interest and account 2 earns 4% simple interest. After one year, the total interest earned from both accounts was $466. Let X be the amount you invested in account 1 and y be the amount invested in account 2
Answers
Answer:
In the account that paid 3% Ramon put $800
In the account that paid 6% Ramon put $1,600
Step-by-step explanation:
Answer:
x+y= 9700 & 0.06x + 0.04y=466
Step-by-step explanation:
let X & Y be each account. Together, they are $9,700.
So, x+y=9700
thus, account 1 (x) earns 6 %. which converted to decimal is 0.06
account 2 (y) earns 4 % which converted is 0.04
It also said that both accounts were $466, after 1 year.
0.06x+0.04y=466
Plz help me I’m stuck
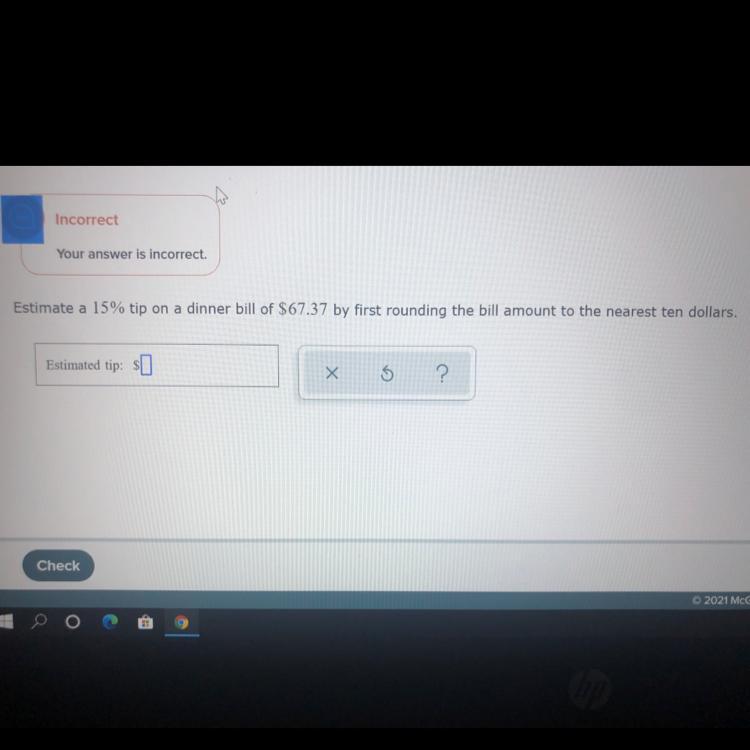
Answers
Answer:
$10.50
Step-by-step explanation:
15% of 70 = $10.50
Hope that helps! (Can you give me a brainliest please? It's ok if you don't!)
Answer: $10
Step-by-step explanation:
15%= 0.15
67.37×0.15= 10.1055 ≈ $10 when rounded to the nearest ten.
HELP ME ASAP!!! YOU WILL BE BRAILIEST!!!!!!!

Answers
Answer:
See step by step.
Step-by-step explanation:
lets define the events:
A: cuban festival C: tropical Garden
B: street art show D: african festival
a) theoretically the probability is
\(P(A)=P(B)=P(C)=P(D)= \frac{1}{4} = 0.25 \\\)
This is 25% (for each one, equally)
b) The experimental probability is given by:
\(P(A)= \frac{32}{150} =0.2133\)
\(P(B)= \frac{38}{150} =0.2533\)
\(P(C)= \frac{35}{150} =0.2333\)
\(P(D)= \frac{45}{150} =0.3000\)
c) The theoretically probabilities are all equally, the experimental probabilities are close to 25% each one, but differ lightly each one, since is an experiment and the result is random.
Is this correct?
f(x)=2x+3
Picture is included

Answers
Answer:
Correct
Step-by-step explanation:
Answer: yessir
Step-by-step explanation:
Troy uses colored sand to make sand art. The storage container for his sand is shaped like a right square prism. He pours some of the sand into a display container shaped like a right triangular prism. When he is done, the height of the sand left in the storage container is 4 in. What is the height of the sand in the display container?

Answers
The height of the sand in the display container is 12 inches when the display container is right triangular prism.
What is right triangular prism ?
A right triangular prism is a three-dimensional geometric shape with two parallel triangular bases and three rectangular faces. The rectangular faces connect the corresponding vertices of the triangular bases.
To find the height of the sand in the display container, we need to use the fact that the volume of sand in the storage container is equal to the volume of sand in the display container.
The storage container has a length, width, and height of 6 inch, 6 inch, and 6inche, respectively. Then, the volume of the storage container is:
\(V_{storage} = L * W * H = 6 * 6 * 6 = 216 inch^3\)
Similarly, let's assume that the display container has a base of length 4 inch and height 9 inches and height of sand be H.
Then, the volume of the display container is:
\(V_{display} = (1/2) * b * h * H = (1/2) * 4 * 9 * H = 18H\)
where (1/2) is the area of the triangle base of the display container.
Since the volumes of sand in both containers are equal, we can set these expressions equal to each other and solve for h:
216 = 18H
H = 12 inches
Therefore, the height of the sand in the display container is 12 inches.
To learn more about volume from the given link :
https://brainly.com/question/22023329
#SPJ1
A professor has learned that three students in his class of 20 will cheat on the final exam. He decides to focus his attention on four randomly chosen students during the exam.
a. What is the probability that he finds at least one of the students cheating? Round your intermediate calculations and final answers to 4 decimal places.Probability_____b. What is the probability that he finds at least one of the students cheating if she focuses on four randomly chosen students? Round your intermediate calculations and final answers to 4 decimal places.Probability_____
Answers
Answer:
a
\(P(X \ge 1) = 0.509 \)
b
\(P(X \ge 1) = 0.6807 \)
Step-by-step explanation:
From the question we are told that
The number of students in the class is N = 20 (This is the population )
The number of student that will cheat is k = 3
The number of students that he is focused on is n = 4
Generally the probability distribution that defines this question is the Hyper geometrically distributed because four students are focused on without replacing them in the class (i.e in the generally population) and population contains exactly three student that will cheat.
Generally probability mass function is mathematically represented as
\(P(X = x) = \frac{^{k}C_x * ^{N-k}C_{n-x}}{^{N}C_n}\)
Here C stands for combination , hence we will be making use of the combination functionality in our calculators
Generally the that he finds at least one of the students cheating when he focus his attention on four randomly chosen students during the exam is mathematically represented as
\(P(X \ge 1) = 1 - P(X \le 0)\)
Here
\(P(X \le 0) = \frac{ ^{3} C_0 * ^{20 - 3} C_{4- 0}}{ ^{20}C_4}\)
\(P(X \le 0) = \frac{ ^{3} C_0 * ^{17} C_{4}}{ ^{20}C_4}\)
\(P(X \le 0) = \frac{ 1 * 2380}{ 4845}\)
\(P(X \le 0) = 0.491\)
Hence
\(P(X \ge 1) = 1 - 0.491\)
\(P(X \ge 1) = 0.509 \)
Generally the that he finds at least one of the students cheating when he focus his attention on six randomly chosen students during the exam is mathematically represented as
\(P(X \ge 1) = 1 - P(X \le 0)\)
\(P(X \ge 1) =1- [ \frac{^{k}C_x * ^{N-k}C_{n-x}}{^{N}C_n}] \)
Here n = 6
So
\(P(X \ge 1) =1- [ \frac{^{3}C_0 * ^{20 -3}C_{6-0}}{^{20}C_6}] \)
\(P(X \ge 1) =1- [ \frac{^{3}C_0 * ^{17}C_{6}}{^{20}C_6}] \)
\(P(X \ge 1) =1- [ \frac{1 * 12376}{38760}] \)
\(P(X \ge 1) =1- 0.3193 \)
\(P(X \ge 1) = 0.6807 \)
Evaluate 4x squared - 8x + 8 when x = -6
Answers
Answer:
44
Step-by-step explanation:
√4×-6+8×6+8=2×-6+48+8
-12+48+8
=48
Hey there!
4x^2 - 8x + 8
= 4(-6)^2 - 8(-6) + 8
= 4(6)(6) - 8(-6) + 8
= 4(36) - (-48) + 8
= 144 - (-48) + 8
= 144 + 48 + 8
= 192 + 8
= 200
Therefore, your answer is: 200
Good luck on your assignment and enjoy your day!
~Amphitrite1040:)
8. Given AABC~AEDC
What is the value of x?
C. 30
D. 20
A. 15
B. 12
A
E
60
X
C
D
10
40
B
Answers
Answer:
790
Step-by-step explanation:
7098uuilu4645
1) The equation c = 2.95g shows how much it costs to buy gas at a gas station on a certain day. In the equation, c represents the cost in dollars, and g represents how many gallons of gas were ppurchased.

Answers
The function of the equation is given below as
\(c=2.95g\)To figure out pairs, we will assume values of g to be 1,2 3,4
Substitute when g is =1
\(\begin{gathered} c=2.95g \\ c=2.95\times1 \\ c=2.95 \end{gathered}\)Substitute when g = 2
\(\begin{gathered} c=2.95g \\ c=2.95\times2 \\ c=5.9 \end{gathered}\)Substitute when g = 3
\(\begin{gathered} c=2.95g \\ c=2.95\times3 \\ c=8.85 \end{gathered}\)Substitute when g = 4
\(\begin{gathered} c=2.95g \\ c=2.95\times5 \\ c=11.8 \end{gathered}\)Hence,
Four pairs that fit in the relationship are
( 1, 2.95 )
( 2, 5.9 )
( 3, 8.85 )
( 4, 11.8 )
b) Sketch a graph of the relationship
The table of values are
The graph of the equation is given below as
C) What does the 2.95 represent?
The 2.95 represents the slope or gradient of the graph
d) Jada's mom said you can get about a third of a gallon of gas for one dollar
The relationship between the cost and the gallons is given below as
\(C=2.95g\)Approminatin the values 2.95 to the nearest whole number, we will have the value to be
\(2.95\approx3\text{ (nearest whole number)}\)So we can say that
\(c=3g\)A third of a gallon is
\(g=\frac{1}{3}\times1=\frac{1}{3}\)\(\begin{gathered} c=3g \\ c=3\times\frac{1}{3} \\ c=1\text{ dollar} \end{gathered}\)Hence,
Jada's mom is correct because a third of a gallon can be approximately bought from one dollar


is 3 a factor of 12
Answers
Answer:YES
Step-by-step explanation:
Answer:
Yes
Step-by-step explanation: the factors of 12 are 1,2,3,4,6 and 12
need help with this please!!

Answers
Answer:
x = -4.
y = 0.
Step-by-step explanation:
Each element is multiplied by -2, so
-2 * x = 8
x = -4.
-2*y = 0
y = 0.
A passenger train leaves depot 2 hours after a freight train leaves the same depot. The freight train is traveling 18 mph slower than the freight train find the rate of each train if the passenger train over, takes the freight train in 3 hours
Answers
Answer:
The passenger train is traveling at 45 mph, and the freight train is traveling at 27 mph.
Step-by-step explanation:
Let's assume the speed of the passenger train is represented by x mph.
According to the given information, the freight train leaves the depot 2 hours before the passenger train. Therefore, when the passenger train starts, the freight train has already been traveling for 2 hours.
Let's represent the speed of the freight train as (x - 18) mph, which is 18 mph slower than the passenger train.
Now, we know that the passenger train overtakes the freight train in 3 hours. This means that the passenger train traveled for 3 hours, while the freight train traveled for 3 + 2 = 5 hours.
Since speed = distance/time, we can set up the following equation based on the distances covered by each train:
Distance covered by passenger train = Distance covered by freight train
Using the formula, distance = speed × time, we get:
x × 3 = (x - 18) × 5
Simplifying the equation:
3x = 5x - 90
90 = 5x - 3x
90 = 2x
Dividing both sides by 2:
45 = x
So, the speed of the passenger train is 45 mph.
The speed of the freight train is 45 - 18 = 27 mph.
1. Use the elimination strategy to solve this linear system:
(1) 12c + 28d = 12 (2) -20c + 16d = 168
2. Determine the number of solutions of this linear system:
(1) 7x − 3y = 43 (2) 7x - 3y = 13
Answers
The solution to the linear system is c = -6 and d = 3.
To solve the linear system using the elimination strategy, we can eliminate one variable by adding or subtracting the equations. Let's solve the first linear system:
(1) 12c + 28d = 12
(2) -20c + 16d = 168
To eliminate one variable, we can multiply equation (1) by 5 and equation (2) by 3, which will result in opposite coefficients for 'c'. This will allow us to eliminate 'c' when adding the equations together:
(1) 60c + 140d = 60
(2) -60c + 48d = 504
Now, we can add the equations:
(60c + 140d) + (-60c + 48d) = 60 + 504
188d = 564
d = 564/188
d = 3
Substituting the value of 'd' back into equation (1):
12c + 28(3) = 12
12c + 84 = 12
12c = 12 - 84
12c = -72
c = -72/12
c = -6
The solution to the linear system is c = -6 and d = 3.
Now let's analyze the second linear system:
(1) 7x - 3y = 43
(2) 7x - 3y = 13
By comparing the two equations, we can see that they have the same coefficients for both 'x' and 'y', and the constant terms on the right side are different. This means the lines represented by the equations are parallel and will never intersect.
The linear system has no solution.
For more questions on linear system
https://brainly.com/question/2030026
#SPJ8
I want to know my grade if I have an 86 and I get a 0 and it’s worth 20% of my grade what will my grade be?
Answers
Answer:
your grade will be an 76
Step-by-step explanation:
How many 1/5s are in 1?

Answers
Answer:
5!
Step-by-step explanation:
What is the degree of the power function represented in the table f(x)
-3, -2, -1, 0, 1, 2, 3
Answers
The degree of the power function represented in the table f(x) is 2.
How to illustrate the information?In order to find the degree of the power function represented in the given table, you must find the difference of the y-values.
The second difference is illustrated as:
2 - 6 = -4.
-2 - 2 = -4
-6 - (-2) = -4
This illustrates that the second differences are constant.
Learn more about functions on:
https://brainly.com/question/5559750
#SPJ1
What is the degree of the power function represented in the table?
1
2
3
4
x h(x)
−2 −8
−1 −2
0 0
1 −2
2 −8
I don’t know this one question

Answers
Answer:
v = 13
Step-by-step explanation:
because they are supplementary angles they add up to 180
so
add them
and put them equal to 180
9v + 3 + 60 = 180
combine like terms
9v + 63 = 180
now subtract 63 to both sides
9v = 117
divide 9 to both sides
v = 13
that is your answer
pleaseeeeeeeeee helpppp i will give extra points

Answers
Answer:
44
Step-by-step explanation:
Answer:
so... its 44
Step-by-step explanation:
2 x 10 = 20
4 x 6 = 24
20 +24 = 44
A company’s cereal boxes advertise that each box contains 9.65 ounces of cereal. In fact, the amount of cereal in a randomly selected box follows a Normal distribution with mean μ = 9.70 ounces and standard deviation σ = 0.03 ounce. Now take an SRS of 5 boxes. What is the probability that the mean amount of cereal in these boxes is less than 9.65 ounces?
What is the probability that the mean amount of cereal ¯
in 5 randomly selected boxes is at most 9.65?
Answers
The probability that the mean amount of cereal in 5 randomly selected boxes is at most 9.65 ounces is 0.4808.
What is the probability?The Central limit theorem is used to find the probability
Data given:
sample size = 5.
mean, μ = 9.70 ounces
standard deviation, σ = 0.03 ounce.
To calculate the probability, we determine the z-score corresponding to the sample mean of 9.65 ounces using the z-score formula.
z = (x - μ) / (σ / √n)wherex is the sample mean,
μ is the population mean,
σ is the population standard deviation, and
n is the sample size.
For the sample mean of 9.65 ounces in 5 boxes:
z = (9.65 - 9.70) / (0.03 / √5)
z ≈ -0.05 / (0.03 / √5)
Using a calculator, we find that the probability is approximately 0.4801.
Therefore, the probability that the mean amount of cereal in 5 randomly selected boxes is less than 9.65 ounces is approximately 0.4801.
Learn more about probability at: https://brainly.com/question/13604758
#SPJ1
A manufacturer claims that its compact fluorescent bulbs contain an average of 1.9 mg of mercury.
State the hypotheses for a two-tailed test, using the manufacturer’s claim about the mean as the null hypothesis.
Multi choice URGENT

Answers
The hypotheses for a two-tailed test, would be A. H0: μ = 1.9 mg ( null hypothesis)
H1: μ ≠ 1.9 mg (alternative hypothesis)
How to find the hypothesis ?The null hypothesis (H0): The population mean of mercury content in compact fluorescent bulbs is equal to 1.9 mg.
Alternative hypothesis (Ha): The population mean of mercury content in compact fluorescent bulbs is not equal to 1.9 mg.
When put into symbols, this becomes H0: μ=1.9 mg vs. H1: μ ≠ 1.9 mg.
Find out more on hypotheses at https://brainly.com/question/30484892
#SPJ1
Classify each function as a power function, root function, polynomial (state its degree), rational function, algebraic function, trigonometric function, exponential function, or logarithmic function.
(a) y=Ï€x
(b) y=xπ
(c) y=x2(2−x3)
(d) y=tant−cost
(e) y=s1+s
(f) y=x3−1√1+x√3
Answers
(a) f(x) = \(log_2(x)\) is a logarithmic function
(b) g(x) = ∜x is a root function
(c) h(x) = \(2x^3/(1 - x^2)\) is a rational function
(d) u(t) = 1 - 1.1t + \(2.54t^2\) is a polynomial of degree 2
(e) v(t) = \(5^t\)is an exponential function
(f) w(θ) = sin θ \(cos^{2}\theta\) is a trigonometric function.
(a) f(x) = \(log_2(x)\) is a logarithmic function. Logarithmic functions have the logarithm of the independent variable as the output. Here, the logarithm base is 2.
(b) g(x) = ∜x is a root function. Root functions have the square root or higher roots of the independent variable as the output. Here, the root is a cube root.
(c) h(x) = \(2x^3/(1 - x^2)\) is a rational function. Rational functions are functions that are expressed as the quotient of two polynomials. Here, the numerator is a cubic polynomial and the denominator is a quadratic polynomial.
(d) u(t) = 1 - 1.1t + \(2.54t^2\) is a polynomial of degree 2. Polynomials are functions that are expressed as a sum of powers of the independent variable, with coefficients. The degree of a polynomial is the highest power of the independent variable.
(e) v(t) = \(5^t\) is an exponential function. Exponential functions have the independent variable as the exponent. Here, the base is 5.
(f) w(θ) = sin θ \(cos^{2}\theta\) is an algebraic function and a trigonometric function. Algebraic functions are functions that can be expressed using arithmetic operations and algebraic expressions. Trigonometric functions are functions that involve the ratios of the sides of a right triangle. Here, the function is a combination of sine and cosine functions.
Read more about functions:
brainly.com/question/28934802
#SPJ4
The complete question is -
Classify each function as a power function, root function, polynomial (state its degree), rational function, algebraic function, trigonometric function, exponential function, or logarithmic function.
(a) f(x) = \(log_2(x)\)
(b) g(x) = ∜x
(c) h(x) = \(2x^3/(1 - x^2)\)
(d) u(t) = 1 - 1.1t + \(2.54t^2\)
(e) v(t) = \(5^t\)
(f) w(θ) = sin θ \(cos^{2}\theta\)
Evaluate each expression. (Round your answers to four decimal places.)
(a) \(10^{2.4}\)
(b) \(6^{-2.6}\)
(c) \(2^{\frac{11}{5}}\)
(d) \(e^{-6}\)
Answers
Answer:
a) 251.1886
b) 0.0095
c) 4.5948
d) .0025
Matt is a salary plus commission salary. He earns a salary of $1,400 and a
commission of 5% of all his sales. This month his sales were $12,852.
Determine how much gross pay did Matt receive for that month.
Answers
Answer:
2042.6$
Step-by-step explanation:
12853(5/100)+1400
What number does y stand for in this equation?
2y - 7 = 35
A
28
B
21
C
14
D
9
Answers
Answer:
B. 21
Step-by-step explanation:
2y=35+7
2y=42
y=42/2
y=21
Prove that if x and y are rational numbers then 5x
2 − 7y is a rational number
Answers
Answer:
It is a rational number
Step-by-step explanation:
140% of what number is 39?
Provide an exact fraction answer.
Answers
Answer:
27.86 or 27 wholes 6/7
Step-by-step explanation:
Let the number be x
140% of x = 39
140x/100 = 39
140x = 3900
x= 3900/140
x = 27 wholes 6/7 or 27.86
help asap ty
will possibly mark brainliest.

Answers
Answer:
Step-by-step explanation:
Letter B is the correct answer
Initial population is 200, tripled every hour
200 x 3 = 600
First hour 200
Second hour = 600 + 200 = 800
Third hour 800x3 = 2400 + 800 = 3200
and so on.
A hat contains 35 marbles. Of them, 20 are red and 15 are green. If one marble is randomly selected out of this hat, what is the probability that this marble is red? Round your answer to two decimal places. P(A) =
Answers
Answer:
P(A) = 0.57 (rounded to two decimal places).
Step-by-step explanation:
The probability of selecting a red marble from the hat can be found by dividing the number of red marbles by the total number of marbles:
P(red) = number of red marbles / total number of marbles
P(red) = 20/35
We can simplify this fraction by dividing both the numerator and denominator by 5:
P(red) = 4/7
So the probability of selecting a red marble from the hat is 4/7, or approximately 0.57 when rounded to two decimal places.
Therefore, P(A) = 0.57 (rounded to two decimal places).