An airplane covers 94 miles in 1/6 of an hour
The airplane can cover blank miles in 6 hours
What is the answer
Answers
Answer:
3384 Miles in 6 hours
Step-by-step explanation:
94 x 6 would equal how many miles the airplane covers in 1 hour.
1 hour equals 564 miles.
564 x 6 equals 3384 miles in 6 hours
Related Questions
Simplify the expression.
4f8 +39) + 5g
Answers
Answer:4f^8+5g+39
Step-by-step explanation:
A taxi ride costs $4 plus an additional $3 per mile. Write the equation for the line in slope-intercept form
Answers
Answer:
y=3x+4
Step-by-step explanation:
4 is your y-intercept, and 3 is your slope.
The linear function shows the total cost will be y = 3x + 4.
What is a linear function?A straight line on the coordinate plane is represented by a linear function.
A linear function always has the same and constant slope.
The formula for a linear function is f(x) = ax + b, where a and b are real values.
As per the given,
A taxi ride costs $4 plus an additional $3 per mile.
Let's say the number of miles is represented as x while the total cost is represented as y.
y = 3x + 4
Hence "The linear function shows the total cost will be y = 3x + 4".
For more about the linear function,
brainly.com/question/21107621
#SPJ2
If the half-life of an element is 67 yr and the initial quantity is 3 kg, write a function of the form Q(t) = Q0 e^-kt to model the quantity of the element left after years. Round k to 4 decimal places.
Would appreciate a step by step explanation, thank you.
Answers
Answer:
A0=3kg
t1/2=67y
λ=ln2/t1/2
λ=0.6931/67
λ=0.0103447761-> 0.0103
Final Amount=Aoe^-λ×t
Final Amount=A0e^-0.0103447761×t
You can put the time that you want to find how much of the material has been left after a certain amount of time
as an example
if t=143years
Final Amount=3×e^-0.0103447761×143
Final Amount=3×e^−1.479302982
Final Amount=0.6833892338
A0 is the amount of material that we have before it goes into radioactive decay
(i will mark brainly)
Use the table to write a proportion.

Answers
Answer:
One proportion is 15 songs / 2.5 hours = 18 songs / h hours.
ok I'll try to answer
first the given 15/2.5=18/h
so the second hour is missing so we have to multiply cross then the result will be
15h=45
divide 15 for 15 and we got h
again divide 45 for 15
[h=3]
Write the equation of the line that goes through the points A(3,-2) and B(5,4)
Answers
Answer:
y = 3x - 11
Step-by-step explanation:
(3, -2) and (5, 4)
m = 4+2/5-3
m = 6/2
m = 3
y = 3x + b
4 = 3(5) + b
4 = 15 + b
b = -11
y = 3x - 11
What is the y-intercept of the graph of the linear function?

Answers
Answer:
-6
Step-by-step explanation:
look at the y-axis (the vertical center line) where it passes through it is the intercept
Solve for x.
Z = блху
О
Z = x
бл
x = -
блуг
Z = x
блу
= x
Answers
Answer
2
Step-by-step explanation:
1 + 1 =2
simplify the expression
4√ 2 + 2√ 32
Answers
Answer:
16.97056
Step-by-step explanation:
A parent is buying two types of chocolate truffles for their family. The oldest child can eat twice as much as their younger siblings and prefers white chocolate (W), the younger three like dark chocolate (D) and the spouse likes white chocolate (W). Five white chocolate truffles (W) cost the same as three dark chocolate truffles (D). If the parent bought 6 white chocolate truffles(W) and 10 dark chocolate truffles (D), and spent $34.00, how much was each dark chocolate truffle
Answers
Answer:
Each chocolate truffle is $2.125
Step-by-step explanation:
Honestly, I'm not 100% sure if this is correct, and I am truly sorry if this is wrong, but its worth a try :)
If TR = 11 ft, find the length of PS. Round to the nearest hundredth.PTR16°Sarc PS =ft

Answers
Given:
TR = 11 Ft
∠RTS = 16°
Let's determine the length of Arc PS,
Step 1: Let's first determine the angle of Arc PS.
∠RTS = 16°
∠PTQ = 16° ; Vertical angle pair of ∠RTS
Since ∠QTR = ∠PTS under the rule of vertical angles, we can now determine the measure of ∠PTS or Arc PS.
We get,
\(\angle RTS\text{ + }\angle PTQ\text{ + }\angle QTR\text{ + }\angle PTS=360\)\(16\text{ + }16\text{ + }\angle PTS\text{ + }\angle PTS=360\)\(32\text{ + }2\angle PTS=360^{}\)\(\angle PTS=\frac{360^{}\text{ - 32}}{2}\)\(\angle PTS=\frac{328}{2}\)\(\angle PTS=164^{\circ}\)Step 2: Let's determine the perimeter of the circle.
\(\text{ Perimeter = }2\pi r\)\(\text{ = 2}\pi(11)\)\(\text{ Perimeter = 22}\pi\)Step 3: Let's determine the length of Arc PS.
\(\text{ Arc Length = (}\frac{\theta}{360})(\text{Perimeter of the Circle)}\)\(\text{ = (}\frac{164}{360})(22)(3.14)\)\(\text{ Arc Length = }31.469777\ldots\text{ }\approx\text{ 31.47 ft.}\)Therefore, the length of Arc PS is 31.47 ft.
standard form
y = -8x + 7
Answers
Y=-1 answer
The triangle is congruent by which triangle congruence theorem ?
SSS
ASA
SAS

Answers
Answer:
SAS
Step-by-step explanation:
Proof:
Side AB ≅ DB (Given)
∠ABC ≅ DBC (Given)
Side BC ≅ Side BC (Reflexive Property of Congruence).
ΔABC ≅ ΔDBC (CPCTC)
~
Which answer describes the pattern in this sequence? 2,1,12,14,... multiply by 2 add 12 subtract 1 multiply by 12
PLEASE ANSWER I NEED THIS DONE BY TOMMOROW
Answers
Answer:hbwufvj6y
Step-by-step explanation:
Given cos x=12/13 and sinx=5/13. What is ratio for tan x ?
Answers
Answer:
5/12
Step-by-step explanation:
tan(x)=sin(x)/cos(x)
So by substitution we have
tan(x)=(5/13)/(12/13)
Multiplying numerator and denominator by 13 gives
tan(x)=5/12
2) What type of equation is compound interest formula?
a)logarithmic
b)polynomial
c)exponential
d)linear
e) none of the choices
Answers
A compound interest formula is a type of exponential equation. That is option C
What are exponential equations?Exponential equations are those equations that has their variables as exponents. A typical example of this type of equation is the compound interest formula.
The compound interest formula is an exponential equation because the little sum invested as capital, once the interest is added, the balance will earn more capital during the next compounding period.
Therefore, a compound interest formula is a type of exponential equation.
Learn more about exponential equations here:
https://brainly.com/question/12940982
you took out a loan for 5,000 and the interest rate was 5.9% which is charged every month if you make no payments how much will your total balance be after 2 months
Answers
+* Answer *+
$5,590
*+Step-by-step explanation:*+
$5,000 x 5.9% = $295
$95 x 2 (months), = 590
5,000 + 590 = 5,590
So therefore you have $5,590 dollars.
hope this helps! : )
Determine if true:
3x5+8=23
Answers
Answer:
True
Step-by-step explanation:
3x5=15
15+8=23
23=23
Answer:
True
Step-by-step explanation:
3 x 5 = 15
15 + 8 = 23
(fractions 5th grade) 2/4 + 3/4=?
Answers
Answer:
5/4
Step-by-step explanation:
They are like fractions.
So, \(\frac{2}{4} + \frac{3}{4}\) can be written as \(\frac{2+3}{4}\)
Thus the answer is \(\frac{5}{4}\).
Mixed Number Form: 1 1/4
Fill in the table using the function rule y=5x-2
Answers
The table has been shown using the function rule y = 5x - 2. (Refer to the table attached below).
What is the function rule?The relationship between the input or domain and the output or range is known as the function rule. If and only if there is a single value in the range for each domain value, a relation is a function.When the provided input values are applied, the function rule y = 2 x + 4 produces the output values displayed in the table. Now, the output numbers " are represented by and the input values are represented by. Consequently, the expression f (x) = 3 x + 1 can be used to represent the function rule y = 3 x + 1.So, the rule is y = 5x - 2:
Now calculate values as follows:
(A) When x = 0:
y = 0 - 2y = - 2(B) When x = 1:
y = 5 - 2y = 3(C) When x = 2:
y = 10 - 2y = 8(D) When x = 3:
y = 15 - 2y = 13Therefore, the table has been shown using the function rule y = 5x - 2. (Refer to the table attached below)
Know more about the function rule here:
https://brainly.com/question/28503724
#SPJ13

Evaluate the following expression. 2\cdot10^4-7^3=2⋅10 4 −7 3 =2, dot, 10, start superscript, 4, end superscript, minus, 7, cubed, equals

Answers
Answer:
19657Step-by-step explanation:
2*10⁴ - 7³ = 2*10*10*10*10 - 7*7*7 = 20000 - 343 = 19657The simplified result of the expression \(2\times 10^{4} - 7^3\) is: 19657.
Here, we have to evaluate the expression \(2\times 10^{4} - 7^3\),
Calculate the exponentials first:
\(10 ^4 =10,000\)
(since \(10 ^4\), means 10 raised to the power of 4)
\(7 ^3 =343\)
(since \(7 ^3\), means 7 raised to the power of 3)
Substitute the values back into the expression:
\(2\times 10^{4} - 7^3\)
=2 × 10000 − 343
Perform the multiplications and subtractions:
2×10,000=20,000
Now subtract 343 from 20,000:
20,000−343=19,657
So, we get,
\(2\times 10^{4} - 7^3\)
=19,657.
The expression involves exponentiation and basic arithmetic operations. We calculate the values of \(10^4\) and \(7^3\) , then substitute those values into the expression.
After performing the multiplications and subtractions, we get the final result of 19,657.
To learn more on multiplication click:
brainly.com/question/5992872
#SPJ3
Which systems of equations have the same solutions?
L (3x+y = 8
1x - 4y = -6
m{$*=*=230
NS 4x – 3y = 2
12% -8y = -12

Answers
Answer:
B. L and N
Step-by-step explanation:
Let's solve each system
✔️System L:
3x + y = 8 => Eqn. 1
x - 4y = -6 => Eqn. 2
x = -6 + 4y
Substitute x = (-6 + 4y) in eqn. 1
3(-6 + 4y) + y = 8
-18 + 12y + y = 8
-18 + 13y = 8
13y = 8 + 18
13y = 26
y = 26/13
y = 2
Substitute y = 2 into Eqn. 2
x - 4y = -6
x - 4(2) = -6
x - 8 = -6
x = -6 + 8
x = 2
Solution to system L = (2, 2)
✔️System M:
4x - 3y = 2 => Eqn. 1
5x - 4y = -30 => Eqn. 2
Multiply eqn 1 by 5, and eqn. 2 by 4
20x - 15y = 10
20x - 16y = -120
Subtract
y = 130
Substitute y = 130 into eqn. 1
4x - 3(130) = 2
4x - 390 = 2
4x = 2 + 390
4x = 392
x = 392/4 = 98
Solution to system M = (98, 130)
✔️System N:
4x - 3y = 2 =>Eqn. 1
2x - 8y = -12 => Eqn. 2
Multiply Eqn. 1 by 2, and eqn. 2 by 4
8x - 6y = 4
8x - 32y = -48
Subtract
26y = 52
y = 52/26
y = 2
Substitute y = 2 into eqn. 1
4x - 3(2) = 2
4x - 6 = 2
4x = 2 + 6
4x = 8
x = 8/4
x = 2
Solution to system N = (2, 2)
in the illustration below ,The two lights are designed tc pperate at 6 volts, 5 amps each,
5
f the power source is12 volts, what will be the value of the Resistor?
Round to the tenth position. (0.00)
Answers
The value of the resistor needed in this scenario is approximately 1.2 ohms.
To find the value of the resistor in the given scenario, we can apply Ohm's Law, which states that the current (I) flowing through a resistor is directly proportional to the voltage (V) across it, and inversely proportional to the resistance (R) of the resistor.
Using Ohm's Law, we have the formula:
V = I * R
Where:
V is the voltage across the resistor (12 volts in this case),
I is the current flowing through the resistor (5 amps for each light, so a total of 10 amps),
R is the resistance of the resistor (which we need to find).
Rearranging the formula, we have:
R = V / I
Plugging in the values:
R = 12 volts / 10 amps
R = 1.2 ohms
Therefore, the value of the resistor needed in this scenario is approximately 1.2 ohms.
It's worth noting that this calculation assumes the lights are connected in parallel, as the current remains the same for each light. If the lights were connected in series, the total resistance would be the sum of the individual resistances, and the calculation would be different.
For more such question on resistor visit:
https://brainly.com/question/4703820
#SPJ8
Example: Divide 3 loaves between 5 people First, divide two of the loaves into thirds... each person gets one third each, with one third left over Then divide the left-over third from the second loaf into fifths So, each person gets: 1/5 and the third loaf into fifths each person gets one fifth each each person gets a slice (one fifteenth) 1/15 3/5 The Egyptians used the approximated process to work on the area of a circle as shown in the picture. 1.4 Show the representation of the fractions on the second row. (2) 1.5 Show the algorithm/abstract strategy to justify the 3/5 found as the answer. (3)
Answers
The algorithm justifies the answer of 3/5 as the fraction each person gets.
Representation of the fractions on the second row:
From what you described, two of the loaves were divided into thirds.
This means each person receives one third, and there is one third remaining. Then, this remaining third from the second loaf was further divided into fifths.
Therefore, each person receives one fifth from this remaining third.
So, the representation of the fractions on the second row would be:
Each person receives 1/3 (one third) from the two loaves.
Each person receives 1/5 (one fifth) from the remaining third.
Algorithm/Abstract strategy to justify the 3/5 found as the answer:
To find the final answer of 3/5, we can follow the steps you provided:
Divide two loaves into thirds, giving each person 1/3.
Divide the remaining third from the second loaf into fifths, giving each person 1/5.
Combining the fractions, each person has 1/3 + 1/5.
To add these fractions, we need to find a common denominator. In this case, the least common multiple (LCM) of 3 and 5 is 15. We can convert 1/3 and 1/5 to have a denominator of 15:
1/3 = 5/15 (multiplying numerator and denominator by 5)
1/5 = 3/15 (multiplying numerator and denominator by 3)
Now, we can add the fractions:
5/15 + 3/15 = 8/15
Therefore, each person receives 8/15 of a loaf.
Simplifying this fraction, we get 3/5.
Hence, the algorithm justifies the answer of 3/5 as the fraction each person gets.
Learn more about Algorithm/Abstract strategy click;
https://brainly.com/question/29438718
#SPJ1
Match each function with the correct translation of the parent function f(x) = x.
160=1x1-4
f(x) = (x+4)
fx)=p+4
0
00
vertical translation down 4 units
horizontal translation right 4 units
horizontal translation left 4 units
vertical translation up 4 units
Answers
It is possible to translate the parent function f(x) = x using various transformations including vertical and horizontal translations. Each transformation will result in
the graph intersecting the x- or y-axis at a different point.
Function is an operation that takes an input, performs some processing on it, and returns a result. It is a set of instructions that performs a specific task. Functions are typically used to perform repetitive tasks, like finding the sum of two numbers, adding two strings together, or finding the maximum of a list of numbers. Functions are essential to programming and can be used to make code more organized, reusable, and efficient.
The function f(x) = x is the parent function for linear equations. This equation is generally used to graph a line with a slope of 1 and a y-intercept of (0, 0). In order to translate this parent function, different transformations are applied to it.
A vertical translation down 4 units would be represented by the equation f(x) = x - 4. This transformation would shift the graph of the parent function down 4 units on the y-axis. This would result in the graph intersecting the y-axis at the point (0, -4).
A horizontal translation right 4 units would be represented by the equation f(x) = x + 4. This transformation would shift the graph of the parent function right 4 units on the x-axis. This would result in the graph intersecting the x-axis at the point (4, 0).
A horizontal translation left 4 units would be represented by the equation f(x) = x - 4. This transformation would shift the graph of the parent function left 4 units on the x-axis. This would result in the graph intersecting the x-axis at the point (-4, 0).
Finally, a vertical translation up 4 units would be represented by the equation f(x) = x + 4. This transformation would shift the graph of the parent function up 4 units on the y-axis. This would result in the graph intersecting the y-axis at the point (0, 4).
In conclusion, it is possible to translate the parent function f(x) = x using various transformations including vertical and horizontal translations. Each transformation will result in the graph intersecting the x- or y-axis at a different point.
To know more about function click-
http://brainly.com/question/25841119
#SPJ1
1. Willow Brook National Bank operates a drive-up teller window that allows customers to complete bank transactions without getting out of their cars. On weekday mornings, arrivals to the drive-up teller window occur at random, with an arrival rate of 24 customers per hour or 0.4 customers per minute.
a. What is the mean or expected number of customers that will arrive in a five-minute period?
b. Assume that the Poisson probability distribution can be used to describe the arrival process. Use the arrival rate in part (a) and compute the probabilities that exactly 0, 1, 2, and 3 customers will arrive during a five-minute period.
c. Delays are expected if more than three customers arrive during any five-minute period. What is the probability that delays will occur?
2. In the Willow Brook National Bank waiting line system (see Problem 1), assume that the service times for the drive-up teller follow an exponential probability distribution with a service rate of 36 customers per hour, or 0.6 customers per minute. Use the exponential probability distribution to answer the following questions:
a. What is the probability that the service time is one minute or less?
b. What is the probability that the service time is two minutes or less?
c. What is the probability that the service time is more than two minutes?
Answers
Answer:
1.
a. 2
b. 0.1353 probability that exactly 0 customers will arrive during a five-minute period, 0.2707 that exactly 1 customer will arrive, 0.2707 that exactly 2 customers will arrive and 0.1805 that exactly 3 customers will arrive.
c. 0.1428 = 14.28% probability that delays will occur.
2.
a. 0.4512 = 45.12% probability that the service time is one minute or less.
b. 0.6988 = 69.88% probability that the service time is two minutes or less.
c. 0.3012 = 30.12% probability that the service time is more than two minutes.
Step-by-step explanation:
Poisson distribution:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:
\(P(X = x) = \frac{e^{-\mu}*\mu^{x}}{(x)!}\)
In which
x is the number of sucesses
e = 2.71828 is the Euler number
\(\mu\) is the mean in the given interval.
Exponential distribution:
The exponential probability distribution, with mean m, is described by the following equation:
\(f(x) = \mu e^{-\mu x}\)
In which \(\mu = \frac{1}{m}\) is the decay parameter.
The probability that x is lower or equal to a is given by:
\(P(X \leq x) = \int\limits^a_0 {f(x)} \, dx\)
Which has the following solution:
\(P(X \leq x) = 1 - e^{-\mu x}\)
The probability of finding a value higher than x is:
\(P(X > x) = 1 - P(X \leq x) = 1 - (1 - e^{-\mu x}) = e^{-\mu x}\)
Question 1:
a. What is the mean or expected number of customers that will arrive in a five-minute period?
0.4 customers per minute, so for 5 minutes:
\(\mu = 0.4*5 = 2\)
So 2 is the answer.
Question b:
\(P(X = x) = \frac{e^{-\mu}*\mu^{x}}{(x)!}\)
\(P(X = 0) = \frac{e^{-2}*2^{0}}{(0)!} = 0.1353\)
\(P(X = 1) = \frac{e^{-2}*2^{1}}{(1)!} = 0.2707\)
\(P(X = 2) = \frac{e^{-2}*2^{2}}{(2)!} = 0.2707\)
\(P(X = 3) = \frac{e^{-2}*2^{3}}{(3)!} = 0.1805\)
0.1353 probability that exactly 0 customers will arrive during a five-minute period, 0.2707 that exactly 1 customer will arrive, 0.2707 that exactly 2 customers will arrive and 0.1805 that exactly 3 customers will arrive.
Question c:
This is:
\(P(X > 3) = 1 - P(X \leq 3)\)
In which:
\(P(X \leq 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)\)
The values we have in item b, so:
\(P(X \leq 3) = 0.1353 + 0.2707 + 0.2707 + 0.1805 = 0.8572\)
\(P(X > 3) = 1 - P(X \leq 3) = 1 - 0.8572 = 0.1428\)
0.1428 = 14.28% probability that delays will occur.
Question 2:
\(\mu = 0.6\)
a. What is the probability that the service time is one minute or less?
\(P(X \leq 1) = 1 - e^{-0.6} = 0.4512\)
0.4512 = 45.12% probability that the service time is one minute or less.
b. What is the probability that the service time is two minutes or less?
\(P(X \leq 2) = 1 - e^{-0.6(2)} = 1 - e^{-1.2} = 0.6988\)
0.6988 = 69.88% probability that the service time is two minutes or less.
c. What is the probability that the service time is more than two minutes?
\(P(X > 2) = e^{-1.2} = 0.3012\)
0.3012 = 30.12% probability that the service time is more than two minutes.
What is the shape of a sorbital
Answers
Answer:
Spherical-Like Shape
Step-by-step explanation:
An s-orbital is spherical with the nucleus at its center.
help asap, I don't understand
help because I'm failing this class.
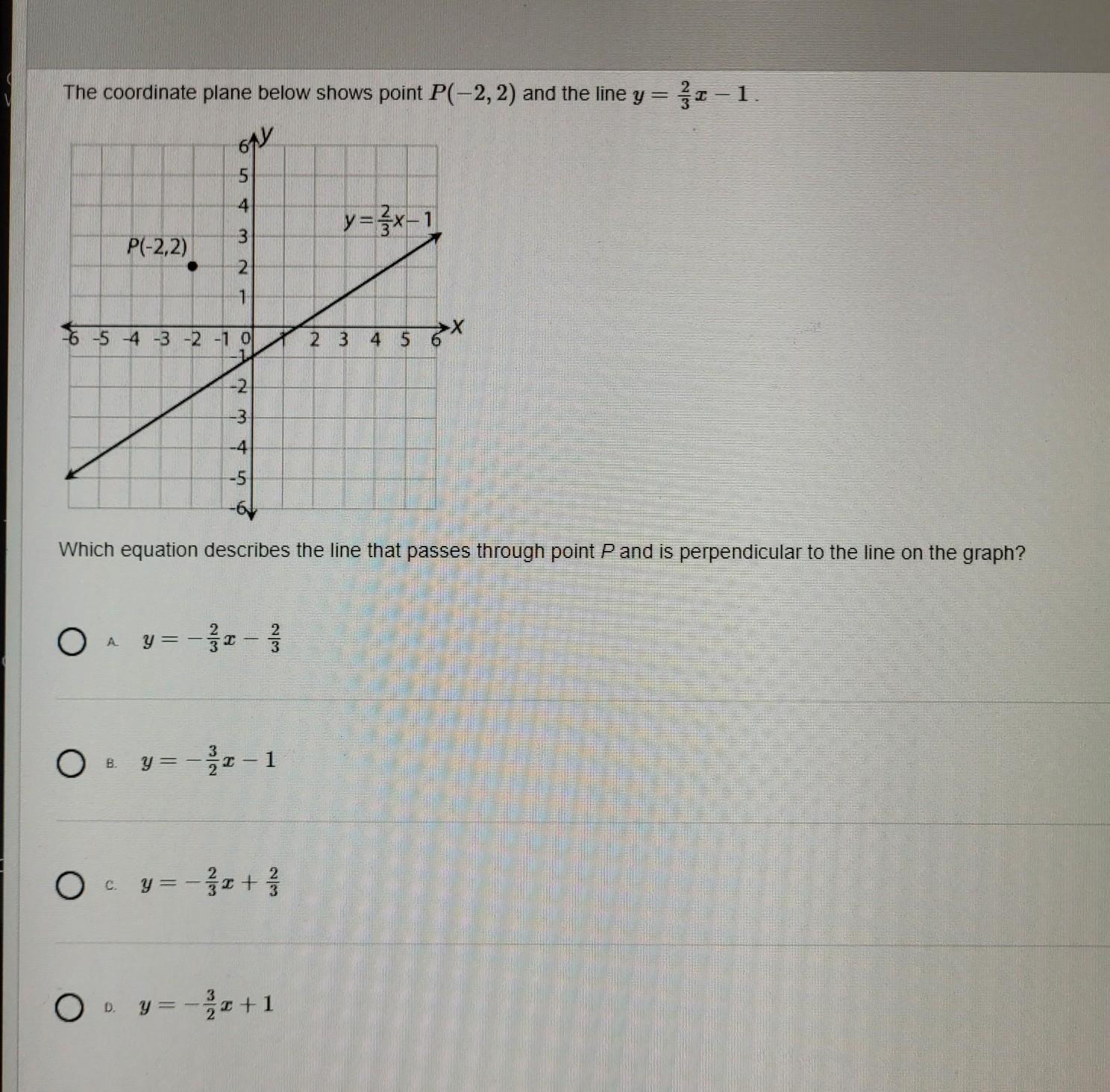
Answers
y = (-3/2)x - 1
================================================
Explanation:
The general slope intercept form is y = mx+b
m = slopeb = y interceptThe slope of the original line in the graph is m = 2/3. Flip the fraction and flip the sign to get -3/2 as the perpendicular slope. The original slope and perpendicular slope multiply to -1.
Since the perpendicular slope is -3/2, this narrows the choices between B and D.
We'll plug this perpendicular slope as the new m value, along with the coordinates of the point (-2,2). Then we solve for the y intercept b value.
So,
y = mx+b
2 = (-3/2)*(-2) + b
2 = -1.5*(-2) + b
2 = 3 + b
2-3 = b
-1 = b
b = -1
With m = -3/2 and b = -1, we have the final answer y = (-3/2)x-1 which is choice B
Side notes:
Because -3/2 = -1.5, that equation in bold is the same as y = -1.5x-1The two perpendicular lines intersect at (0,-1). They both have the same y intercept. This won't always happen for any two random perpendicular lines.If you started at P(-2,2) and dropped down 3, and moved to the right 2, then you arrive at (0,-1).given f(x)= 24x^3+14x^2-11x-6 and (2x+1) is a factor, write f(x) as a set of linear factors
Answers
The linear factors of the given polynomial is (2x+1)(4x+3) and (3x-2).
What is factorization?The factorization method uses basic factorization formula to reduce any algebraic or quadratic equation into its simpler form, where the equations are represented as the product of factors instead of expanding the brackets. The factors of any equation can be an integer, a variable, or an algebraic expression itself.
The given function is f(x)=24x³+14x²-11x-6 and one of the factor is (2x+1).
Here, 24x³+14x²-11x-6 can be written as 24x³+12x²+2x²+1x-12x-6
12x²(2x+1)+1x(2x+1)-6(2x+1)
= (2x+1)(12x²+1x-6)
= (2x+1)(12x²+1x-6)
= (2x+1)(12x²+9x-8x-6)
= (2x+1)[3x(4x+3)-2(4x+3)]
= (2x+1)(4x+3)(3x-2)
Therefore, the linear factors of the given polynomial is (2x+1)(4x+3) and (3x-2).
To learn more about the factorization visit:
https://brainly.com/question/26923098.
#SPJ9
using the centriod explain the relationship between point z and the triangle. justify with applicable theorem.
4. if the length of gu is 18 units, what is the length of gz?
5. if the length of zt is 4.8 units, what is the length of ot?
show all work

Answers
Length of gz = 12 units
Length of ot = 14.4 units
Given,
Triangle EGD with centroid at Z .
Now,
As we know that centroid divides the line segment in the ratio 2:1 .
Firstly calculate the length of gz,
gu = 18 unit
gz:zu = 2:1
gz = 2/3 * 18
gz = 12 units .
Secondly calculate the length of ot,
zt = 4.8 units
oz:zt = 2:1
oz = 4.8 * 2
oz = 9.6 units
ot = 9.6+ 4.8
ot = 14.4 units
Hence with the centroid length of ot and gz can be found out .
Know more about triangles,
https://brainly.com/question/30420011
#SPJ1
Find the mean, median, and mode of the following data. If necessary, round to one more decimal place than the largest number of decimal places given in the data. Lengths of Longest 3 Point Kick for NCAA Division 1-A Football (in Yards) 32 46 48 44 31 36 56 59 32 31 55 52 58 40 59 46 35 49 59 37 ev Copy Data Keypad m Tables Answer 2 Points Separate multiple answers with commas, if necessary. Selecting a button will replace the entered answer value(s) with the button value. If the button is not selected, the entered answer is used Mean:
Answers
The mean, median, and mode of the data Lengths of Longest 3 Point Kick for NCAA Division 1-A Football 32 46 48 44 31 36 56 59 32 31 55 52 58 40 59 46 35 49 59 37 is :
Mean: 45.3Median: 46Mode: 59Mean of the data set can be calculated as,
Mean = ∑xi/n
Here number of sample(n) = 20
So Mean,
(32+46+49+44+31+36+56+59+32+31+55+52+58+40+59+46+35+49+59+37)/20
= 905/20
= 45.25 or 45.3
Median can be calculated as,
Median = (n+1)/2 = (20+1)/2 th value = 10.5th value
Now we will sort the data from smallest to largest data value as follows
31,31,32,32,35,36,37,40,44,46,46,48,49,52,55,56,58,59,59,59
So 10th value from the sorted data is 46 and 11th value is 46
So Median = (46+46)/2 = 46
Mode of the data set is 59 as this value is occuring most of the times in the data set.
Learn more about Mean, mode, median:
https://brainly.com/question/29258804
#SPJ4