an education expert is researching teaching methods and wishes to interview teachers from a particular school district. she randomly selects ten schools from the district and interviews all of the teachers at the selected schools. does this sam
Answers
The sampling plan described does not result in a random sample or a simple random sample as the schools and teachers were not randomly selected from the entire population of teachers in the district.
A random sample involves selecting participants randomly from the entire population, ensuring that each member of the population has an equal chance of being included.
However, in this case, the education expert has specifically chosen ten schools from the district. This targeted selection of schools does not represent a random sampling process.
Furthermore, a simple random sample involves randomly selecting individuals from the population without any restrictions or pre-defined criteria.
In this scenario, the expert has interviewed all the teachers at the selected schools, which means that the sample is not randomly chosen from the individual teachers in the district.
To know more about sampling plan:
https://brainly.com/question/32365842
#SPJ4
--The given question is incomplete, the complete question is given below " An education expert is researching teaching methods and wishes to interview teachers from a particular school district. She randomly selects ten schools from the district and interviews all of the teachers at the selected schools. Does this sampling plan result in a random sample? Simple random sample? Explain."--
Related Questions
What is the equivalent of 20
Answers
Answer:
Step-by-step expla... how to find them. Multiply the numerator and denominator by the same whole number to create an equivalent fraction. Calculator finds 20 equivalent fractions.
I need help to find the measures and equation pls.

Answers
Answer:
Equation: 7x + 8x = 180
x = 12
∠CBA = 84
∠CFH = 96
Step-by-step explanation:
We can see that ∠CBA = ∠CFE and ∠CBD = ∠CFH.
We know that the sums of two angles on a straight line are going to be equal to 180.
∠CBA = 7x
∠CFH = 8x
To find the value of x, we must do the following:
7x + 8x = 180
15x = 180
15x/15 = 180/15
x = 12
Now we just substitute to find the angle measures:
∠CBA = 7 · 12 = 84
∠ CFH = 8 · 12 = 96
Find the value of x in the figure.

Answers
Step-by-step explanation:
✧ \( \underline{ \underline{ \large{ \tt{S \: O \: L \: U \: T \: I \: O \: N}}}} : \)
~Set up an equation and solve for x :
→ \( \large{ \tt{10x + 45 \degree = 75 \degree + 70 \degree}}\) [ Exterior angle is always equal to the sum of two non-adjacent interior angles ]
Add the numbers : 75° & 70°
→ \( \large{ \tt{10x + 45 \degree = 145 \degree}}\)
Since we want to get rid of the constant in the left hand side , subtract 45 from both sides :
→ \( \large{ \tt{10x + 45 \degree - 45 \degree= 145 \degree - 45 \degree}}\)
→ \( \large{ \tt{10x \: \cancel{ + 45 \degree} \: \cancel{ - 45 \degree} = 100 \degree}}\)
→ \( \large{ \tt{10x = 100 \degree}}\)
~Divide both sides by 10
→ \( \large{ \tt{ \frac{10x}{10} = \frac{100}{10}}} \degree\)
→ \( \large{ \tt{x = 10 \degree}}\)
⟿ \( \boxed{ \boxed{ \large{ \text{Our \: Final \: Answer} : \underline{ \bold{ \tt{x = 10 \degree}}}}}}\)
Hope I helped ! ツ
Have a wonderful day / night ! ♡
☄Let me know if you have any questions regarding my answer !
♪ \( \underline{ \underline{ \mathfrak{Carry \: On \: Learning}}}\) !! ✎
▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁
Please answer number 9.
I've drawn the dimensions, I just need help with labeling.

Answers
The polygon which on rotated gives the given cylinder is a rectangle with dimensions 10 inches × 9 inches.
Given a cylinder with the diameter of the base 18 inches and the height of the cylinder 10 inches.
This cylinder is formed by rotating some polygon around YZ.
The polygon must be a rectangle which has the height or the length equal to the height of the cylinder.
So length = 10 inches
The width of the rectangle will be half of the diameter.
Width = 18/2 = 9 inches
Hence the rotated polygon is a rectangle with length 10 inches and width 9 inches.
Learn more about Rotation here :
https://brainly.com/question/2192442
#SPJ1
Find the Tangent vector, the Normal vector, and the Binormal vector (→T, →N and →B) for the curve →r(t)=〈4cos(2t),4sin(2t),5t〉 at the point t=0. Round answers to 3 decimal places.
T(0) =0=[sqrt(89)= sqrt(89)]
N(0) =[ ]
B(0) =[ ]
Answers
The tangent vector → \(r(t)=〈4cos(2t),4sin(2t),5t〉\), normal vector at t=0 is given by →N(0) = 〈-1,0,0〉, and binormal vector at t=0 is given by →\(B(0) = 〈0, -0.441, -0.898〉\)
The tangent vector, normal vector, and binormal vector of the given curve are as follows:
Given curve:
→ \(r(t)=〈4cos(2t),4sin(2t),5t〉\) at the point t=0
To find: Tangent vector, the Normal vector, and the Binormal vector (→T, →N and →B) at the point t=0
Tangent vector: To find the tangent vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\) at the point t=0,
we need to differentiate the equation of the curve with respect to t.t = 0, we have:
→\(r(t) = 〈4cos(2t),4sin(2t),5t〉→r(0) = 〈4cos(0),4sin(0),5(0)〉= 〈4,0,0〉\)
Differentiating w.r.t t:→\(r(t) = 〈4cos(2t),4sin(2t),5t〉 → r'(t) = 〈-8sin(2t),8cos(2t),5〉t = 0\),
we have:
→\(r'(0) = 〈-8sin(0),8cos(0),5〉= 〈0,8,5〉\)
Therefore, the tangent vector at t = 0 is given by
→\(T(0) = r'(0) / |r'(0)|= 〈0,8,5〉 / sqrt(89)≈〈0.000,0.898,0.441〉\)
Normal vector:To find the normal vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0, we need to differentiate the equation of the tangent vector with respect to t.t = 0, we have:
→\(T(0) = 〈0.000,0.898,0.441〉\)
Differentiating w.r.t t:
→\(T'(t) = 〈-16cos(2t),-16sin(2t),0〉t = 0\),
we have:
→\(T'(0) = 〈-16cos(0),-16sin(0),0〉= 〈-16,0,0〉\)
Therefore, the normal vector at t = 0 is given by
→\(N(0) = T'(0) / |T'(0)|= 〈-16,0,0〉 / 16= 〈-1,0,0〉\)
Binormal vector: To find the binormal vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0, we need to cross-product the equation of the tangent vector and normal vector of the curve.t = 0, we have:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉\)
The cross product of two vectors:
→\(B(0) = →T(0) × →N(0)= 〈0.000,0.898,0.441〉 × 〈-1,0,0〉= 〈0, -0.441, -0.898〉\)
Therefore, the binormal vector at t = 0 is given by→B(0) = 〈0, -0.441, -0.898〉
Hence, the tangent vector, normal vector, and binormal vector of the given curve at t=0 are as follows:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉→B(0) = 〈0, -0.441, -0.898〉\)
The given curve is
→\(r(t)=〈4cos(2t),4sin(2t),5t〉 at the point t=0.\)
We are asked to find the tangent vector, the normal vector, and the binormal vector of the given curve at t=0.
the tangent vector at t=0. To find the tangent vector, we need to differentiate the equation of the curve with respect to t. Then, we can substitute t=0 to find the tangent vector at that point. the equation of the curve Is:
→\(r(t) = 〈4cos(2t),4sin(2t),5t〉\)
At t = 0, we have:
→\(r(0) = 〈4cos(0),4sin(0),5(0)〉= 〈4,0,0〉\)
We can differentiate this equation with respect to t to get the tangent vector as:
→\(r'(t) = 〈-8sin(2t),8cos(2t),5〉\)
At t=0, the tangent vector is:
→\(T(0) = r'(0) / |r'(0)|= 〈0,8,5〉 / sqrt(89)≈〈0.000,0.898,0.441〉\)
Next, we find the normal vector. To find the normal vector, we need to differentiate the equation of the tangent vector with respect to t. Then, we can substitute t=0 to find the normal vector at that point.
At t=0, the tangent vector is:
→\(T(0) = 〈0.000,0.898,0.441〉\)
Differentiating this equation with respect to t, we get the normal vector as:
→\(T'(t) = 〈-16cos(2t),-16sin(2t),0〉\)
At t=0, the normal vector is:
→\(N(0) = T'(0) / |T'(0)|= 〈-16,0,0〉 / 16= 〈-1,0,0〉\)
Finally, we find the binormal vector. To find the binormal vector, we need to cross-product the equation of the tangent vector and the normal vector of the curve.
At t=0, we can cross product →T(0) and →N(0) to find the binormal vector.
At t=0, the tangent vector is:
→\(T(0) = 〈0.000,0.898,0.441〉\)
The normal vector is:
→N(0) = 〈-1,0,0〉Cross product of two vectors →T(0) and →N(0) is given as:
→\(B(0) = →T(0) × →N(0)= 〈0.000,0.898,0.441〉 × 〈-1,0,0〉= 〈0, -0.441, -0.898〉\)
Therefore, the tangent vector, normal vector, and binormal vector of the given curve at t=0 are:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉→B(0) = 〈0, -0.441, -0.898〉\)
The tangent vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0 is given by →\(T(0) = 〈0.000,0.898,0.441〉.\)
The normal vector at t=0 is given by →N(0) = 〈-1,0,0〉.
The binormal vector at t=0 is given by →B(0) = 〈0, -0.441, -0.898〉.
To know more about binormal vectors visit
brainly.com/question/31673319
#SPJ11
1. Describe the relationship you see between elevation and temperature in these data sets.
Answers
In response to the stated question, we may state that The scatter plot indicates a clustering pattern in the data, and as elevation increases, temperature drops.
What exactly is a scatter plot?"Scatter plots are graphs that show the association of two variables in a data collection. It is a two-dimensional plane or a Cartesian system that represents data points. The X-axis represents the independent variable or characteristic, while the Y-axis represents the dependent variable. These plots are sometimes referred to as scatter graphs or scatter diagrams."
"A scatter plot is also known as a scatter chart, scattergram, or XY graph. The scatter diagram plots numerical data pairings, one variable on each axis, to demonstrate their connection."
Because the graph is a scatter plot, the data displays a clustering pattern.
We may deduce from the figure that as height increases, temperature falls.
As a result, C and E are the proper choices.
To know more about scatter plot visit:
https://brainly.com/question/13984412
#SPJ1
The correct question is -
The scatter plot shows the relationship between elevation and temperature on a certain mountain peak in North America. Which statements are correct?
A. The data shows one potential outlier
B. The data shows a linear association
C. The data shows a clustering pattern
D. The data shows a negative association
E. As elevation increases, temperature decreases
Solve for y. 4y+5/3=y-10/2
Answers
Answer:
20/9
Step-by-step explanation:
Answer:
\(y = - \frac{20}{9} \)
Step-by-step explanation:
\(4y + \frac{5}{3} = y - \frac{10}{2} \\ 4y + \frac{5}{3} = y - 5 \\ 4y - y = - 5 - \frac{5}{3} \\ 3y = - \frac{20}{3} \times \frac{1}{3} \)
\( y = - \frac{20}{9} \)
Can someone help me with this ( pls don't use links) the first one who answers this gets 5 stars

Answers
Answer: 4 = 90
Step-by-step explanation:
90
Answer:
1. 135° = obtuse angle
2. 245° = Reflex angle
3. 62° = acute angle
4. 110° = obtuse reflex angle
Express each statement using an inequality involving absolute value. A. The weatherman predicted that the temperature would be within 39 of 52°F. B. Serena will make the B team if she scores within 8 points of the team average of 92.
Answers
We can write the inequality involving absolute value to express the statement as:
|x - 52| ≤ 39 Where x is the temperature in degrees Fahrenheit.
The inequality involving absolute value to express the statements are:
A. The weatherman predicted that the temperature would be within 39 of 52°F.
We can write the inequality involving absolute value to express the statement as:
|x - 52| ≤ 39
Where x is the temperature in degrees Fahrenheit.
This absolute value inequality states that the temperature should be within 39°F of 52°F. Hence, the temperature can be 13°F or 91°F. However, if the temperature goes beyond these limits, then it is not within 39 of 52°F.B. Serena will make the B team if she scores within 8 points of the team average of 92.
We can write the inequality involving absolute value to express the statement as:
|x - 92| ≤ 8
Where x is the score obtained by Serena. This absolute value inequality states that the score obtained by Serena should be within 8 points of the team average of 92. Hence, if the average score is 92, then Serena can score between 84 and 100. However, if Serena's score goes beyond these limits, then she will not make it to the B team.
To know more about inequality visit:
https://brainly.com/question/20383699
#SPJ11
The information below is based on independent random samples taken from two normally distributed populations having equal variances. Based on the sample information, determine the 90% confidence interval estimate for the difference between the two population means n₁ 19 X₁ = 54 $1 = 8 n₂ = 11 X₂ = 50 $₂=7
Answers
we can calculate the confidence interval using the formula mentioned earlier, CI = (X₁ - X₂) ± t * sqrt((s₁²/n₁) + (s₂²/n₂))
= (54 - 50) ± 1.701 * sqrt((42.11/19) + (s₂²/11))
To determine the 90% confidence interval estimate for the difference between the two population means, we can use the two-sample t-test formula. The formula for the confidence interval is:
CI = (X₁ - X₂) ± t * sqrt((s₁²/n₁) + (s₂²/n₂))
Where:
X₁ and X₂ are the sample means of the two populations.
n₁ and n₂ are the sample sizes of the two populations.
s₁² and s₂² are the sample variances of the two populations.
t is the critical value from the t-distribution based on the desired confidence level and the degrees of freedom.
In this case, we have:
X₁ = 54, X₂ = 50 (sample means)
n₁ = 19, n₂ = 11 (sample sizes)
$₁ = 8, $₂ = unknown (population variances)
First, we need to calculate the sample variances, s₁² and s₂². Since the population variances are unknown, we can estimate them using the sample variances. The formula for the sample variance is:
s² = ((n - 1) * $²) / (n - 1)
For the first sample:
s₁² = ((19 - 1) * 8²) / 19 ≈ 42.11
Now, we can calculate the degrees of freedom (df) using the formula:
df = (n₁ - 1) + (n₂ - 1) = 18 + 10 = 28
Next, we need to find the critical value (t) from the t-distribution with a confidence level of 90% and 28 degrees of freedom. Using a t-table or a statistical software, we find that t = 1.701.
Finally, we can calculate the confidence interval using the formula mentioned earlier:
CI = (X₁ - X₂) ± t * sqrt((s₁²/n₁) + (s₂²/n₂))
= (54 - 50) ± 1.701 * sqrt((42.11/19) + (s₂²/11))
Since we don't have the value of $₂, we cannot calculate the exact confidence interval without additional information.
To know more about interval refer here:
https://brainly.com/question/11051767#
#SPJ11
9 1/10 - 4 3/4
Help please
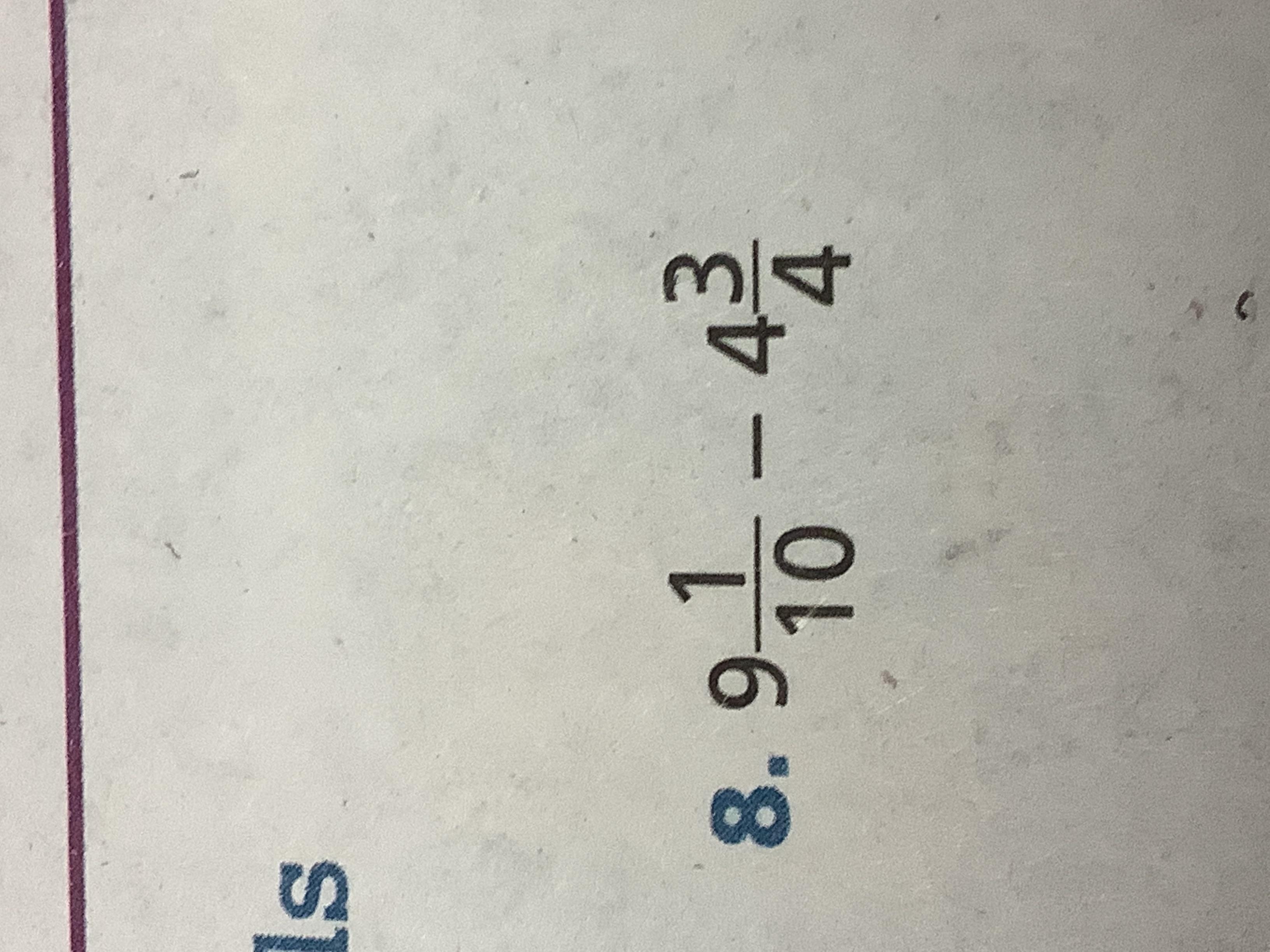
Answers
Answer:
\(4\frac{7}{20}\)
Hope This Helps! :)
Answer:
\(4\frac{7}{20}\)
Step-by-step explanation:
\(9\frac{1}{10}-4\frac{3}{4}\)
Convert in improper fractions:
\(\frac{10*9+1 }{10} -\frac{4*4+3}{4}\\\\\frac{90+1}{10}-\frac{16+3}{4}\\\\\frac{91}{10}-\frac{19}{4} < ==find\ the\ LCM\ or\ the\ common\ denominator\ for\ 10\ and\ 4\ (20)\\\\\frac{182}{20} -\frac{95}{20}\\\\ \frac{87}{20} < ==convert\ to\ a\ mixed\ fraction\\\\ 4\frac{7}{20}\)
Multiples of 4:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40
Multiples of 10:
10, 20, 30, 40
LCM of 4 and 10 is 20.
Hope this helps!
YALL IS ANYONE WILLING TO SOLVE MATH?

Answers
Answer:
A = 1160
B = 1160 is already in standard form.
C = 1200
Evaluate the following by using suitable
Identity
202×205
99²
Answers
Answer:
202×205= 41410
99²= 9801
Step-by-step explanation:
se the divergence theorem to calculate the surface integral s f · ds; that is, calculate the flux of f across s. f(x, y, z)
Answers
The value of the surface integral or flux is \(\(2\pi\)\) for the given vector field \(\(\mathbf{f}\)\) across the surface defined by the unit sphere centered at the origin.
To properly solve the problem, let's consider a specific example. Suppose we have the vector field \(\(\mathbf{f}(x, y, z) = x^2\mathbf{i} + y^2\mathbf{j} + z^2\mathbf{k}\)\), and we want to calculate the surface integral or flux of \(\(\mathbf{f}\)\) across the surface \(\(S\)\) defined by the unit sphere centered at the origin.
Using the divergence theorem, the surface integral can be calculated as follows:
\(\[\iint_S \mathbf{f} \cdot d\mathbf{S} = \iiint_V \nabla \cdot \mathbf{f} \, dV\]\)
Since \(\(\nabla \cdot \mathbf{f} = \frac{\partial}{\partial x}(x^2) + \frac{\partial}{\partial y}(y^2) + \frac{\partial}{\partial z}(z^2) = 2x + 2y + 2z\)\), the triple integral becomes:
\(\[\iiint_V (2x + 2y + 2z) \, dV\]\)
Considering the unit sphere as the volume \(\(V\)\), we can switch to spherical coordinates with \(\(x = \rho\sin\phi\cos\theta\), \(y = \rho\sin\phi\sin\theta\), and \(z = \rho\cos\phi\), and \(\rho\) ranging from 0 to 1, \(\phi\) ranging from 0 to \(\pi\), and \(\theta\) ranging from 0 to \(2\pi\).\)
To further solve the problem, let's evaluate the triple integral using the given limits and spherical coordinates:
\(\[\iiint_V (2x + 2y + 2z) \, dV\]\)
In spherical coordinates, the volume element \(\(dV\) becomes \(\rho^2 \sin \phi \, d\rho \, d\phi \, d\theta\)\).
Substituting the coordinates and limits into the triple integral, we have:
\(\iiint_V (2x + 2y + 2z) \, dV &= \int_0^{2\pi} \int_0^{\pi} \int_0^1 (2\rho\sin\phi\cos\theta + 2\rho\sin\phi\sin\theta + 2\rho\cos\phi) \rho^2 \sin \phi \, d\rho \, d\phi \, d\theta \\\)
\(&= \int_0^{2\pi} \int_0^{\pi} \int_0^1 (2\rho^3\sin^2\phi\cos\theta + 2\rho^3\sin^2\phi\sin\theta + 2\rho^2\sin\phi\cos\phi) \, d\rho \, d\phi \, d\theta \\\)
\(&= \int_0^{2\pi} \int_0^{\pi} \left[\frac{1}{2}\rho^4\sin^2\phi\cos\theta + \frac{1}{2}\rho^4\sin^2\phi\sin\theta + \frac{2}{3}\rho^3\sin\phi\cos\phi\right]_0^1 \, d\phi \, d\theta \\\)
\(&= \int_0^{2\pi} \int_0^{\pi} \left(\frac{1}{2}\sin^2\phi\cos\theta + \frac{1}{2}\sin^2\phi\sin\theta + \frac{2}{3}\sin\phi\cos\phi\right) \, d\phi \, d\theta\end{aligned}\]\)
Evaluating the inner integral with respect to \(\(\phi\)\), we get:
\(\[\int_0^{\pi} \left(\frac{1}{2}\sin^2\phi\cos\theta + \frac{1}{2}\sin^2\phi\sin\theta + \frac{2}{3}\sin\phi\cos\phi\right) \, d\phi = \frac{\pi}{2}\]\)
Substituting this result into the outer integral with respect to \(\(\theta\)\), we have:
\(\[\int_0^{2\pi} \frac{\pi}{2} \, d\theta = \pi \cdot 2 = 2\pi\]\)
Therefore, the value of the surface integral or flux is \(\(2\pi\)\) for the given vector field \(\(\mathbf{f}\)\) across the surface defined by the unit sphere centered at the origin.
To know more about divergence visit -
brainly.com/question/19699905
#SPJ11
1 and 2 is all I need and you guys would help me from not getting beat

Answers
Answer:
1. -10
2. -11
Step-by-step explanation:
the profit p (in dollars) generated by selling x units of a certain commodity is given by the function p ( x ) = - 1500 + 12 x - 0.004 x ^ 2 What is the maximum profit, and how many units must be sold to generate it?
Answers
The profit (p) is $7500 generated by selling 1500 units of a certain commodity is given by the function p ( x ) = - 1500 + 12 x - 0.004 x²
To maximize our profit, we must locate the vertex of the parabola represented by this function. The x-value of the vertex indicates the number of units that must be sold to maximize profit.
We may use the formula for the x-coordinate of a parabola's vertex:
x = -b/2a
where a and b represent the coefficients of the quadratic function ax² + bx + c. In this situation, a = -0.004 and b = 12, resulting in:
x = -12 / 2(-0.004) = 1500
This indicates that when 1,500 units are sold, the profit is maximized.
To calculate the greatest profit, enter x = 1500 into the profit function:
P(1500) = -1500 + 12(1500) - 0.004(1500)^2
P(1500) = -1500 + 18000 - 9000
P(1500) = $7500
Therefore, the maximum possible profit is $7,500 and it is generated when 1,500 units are sold.
Learn more about Profit maximization:
https://brainly.com/question/30436087
#SPJ4
To achieve this maximum profit, exactly 1500 units must be sold.
To find the maximum profit and the number of units needed to generate it, we can use the given profit function p(x) = -1500 + 12x - 0.004x^2. We need to find the vertex of the parabola represented by this quadratic function, as the vertex will give us the maximum profit and the corresponding number of units.
Step 1: Identify the coefficients a, b, and c in the quadratic function.
In p(x) = -1500 + 12x - 0.004x^2, the coefficients are:
a = -0.004
b = 12
c = -1500
Step 2: Find the x-coordinate of the vertex using the formula x = -b / (2a).
x = -12 / (2 * -0.004) = -12 / -0.008 = 1500
Step 3: Find the maximum profit by substituting the x-coordinate into the profit function p(x).
p(1500) = -1500 + 12 * 1500 - 0.004 * 1500^2
p(1500) = -1500 + 18000 - 0.004 * 2250000
p(1500) = -1500 + 18000 - 9000
p(1500) = 7500
So, the maximum profit is $7,500, and 1,500 units must be sold to generate it.
To learn more about parabola: brainly.com/question/8227487
#SPJ11
What is the volume of a cone with a diameter of 8 in and a height of 5 in?
Answers
Answer:
V=80π/3 or V=83.78
Step-by-step explanation:
The volume is
V=πr^2h/3
r=4 (because the radius is half the diameter)
h=5
V=π16*5/3
V=80π/3
Answer:
83.73
Step-by-step explanation:
volume = (1/3) · π · r2 · h
volume = (1/3) x 3.14 x 4^2 x 5
volume = (1/3) x 3.14 x 16 x 5
3.14 x 16 x 5 = 251.2
1/3 x 251.2
83.73
Harvey decided to make chocolate pudding pies for a celebration. He had to make 4 pies. Each pie needed 2 quarts of milk. How many pints of milk will he need?
Answers
Answer:
He will need 16 pints.
Step-by-step explanation:
2 pints per quart
2 quarts = 4 pints
4 x number of pies (4)
16
Answer
16 pints.
2 pints per quart
2 quarts makes 4 pints
4 x number of pies
16c
I think
In making a dot plot for the data set, how would you scale the number line?Data set: 10, 8, 8, 15, 12, 14, 12, 14, 10, 10, 8A)8 to 14 in increments of 1B)8 to 15 in increments of 1C)0 to 15 in increments of 1D)0 to 15 in increments of3
Answers
Arranging the data set in increasing order:
8, 8, 8, 10, 10, 10, 12, 12, 14, 14, 15
We have to have plots at each of these unique numbers.
So,
We will make the dot plot from 8 to 15 and basically have increments of 1.
B is the correct choice.
Solve the system 2y 2y If the system has infinitely many solutions, express your answer in the form x = x and y as a function of x X = y= 3x X + = = –4 4 Solve the system using elimination X = y = -8x +3y - 2y 5x = = -17 11
Answers
The solution to the given system of equations is x = -1/10 and y = 8/5.
To solve the given system of equations using elimination, let's write the system in standard form:
2x + 2y = 3 ...(1)
8x - 2y = -4 ...(2)
To eliminate the y-variable, we'll multiply equation (1) by 1 and equation (2) by 2:
2x + 2y = 3 ...(1)
16x - 4y = -8 ...(2)
Now, we can add equation (1) and equation (2) to eliminate the y-variable:
(2x + 2y) + (16x - 4y) = 3 + (-8)
18x - 2y = -5
Simplifying the equation, we get:
18x - 2y = -5 ...(3)
Now, let's eliminate the y-variable again. We'll multiply equation (1) by 2 and equation (3) by -1:
4x + 4y = 6 ...(1)
-18x + 2y = 5 ...(3)
Adding equation (1) and equation (3)
(4x + 4y) + (-18x + 2y) = 6 + 5
-14x + 6y = 11
Simplifying the equation, we get:
-14x + 6y = 11 ...(4)
Now we have two equations:
18x - 2y = -5 ...(3)
-14x + 6y = 11 ...(4)
To eliminate the y-variable again, we'll multiply equation (3) by 3 and equation (4) by 1:
54x - 6y = -15 ...(3)
-14x + 6y = 11 ...(4)
Adding equation (3) and equation (4):
(54x - 6y) + (-14x + 6y) = -15 + 11
40x = -4
Dividing both sides by 40, we find:
x = -4/40
x = -1/10
Now, we can substitute the value of x into any of the equations to solve for y. Let's use equation (1):
2x + 2y = 3
Substituting x = -1/10:
2(-1/10) + 2y = 3
-1/5 + 2y = 3
2y = 3 + 1/5
2y = 16/5
y = 8/5
Therefore, the solution to the given system of equations is x = -1/10 and y = 8/5.
Learn more about standard form here:
https://brainly.com/question/17264364
#SPJ11
John owed his brother $25.75, but was able to pay him back $19.45. How much does John owe brother owe now?
Answers
Answer:
$6.30
Step-by-step explanation:
So we are going to subtract what is owed by what is payed back to find out how much John owes his brother
$25.75 - $19.45 = $6.30
John owes his brother $6.30
Andres is going to invest in an account paying an interest rate of 4% compounded
continuously. How much would Andres need to invest, to the nearest dollar, for the
value of the account to reach $4,700 in 11 years?
Answers
\(~~~~~~ \textit{Continuously Compounding Interest Earned Amount} \\\\ A=Pe^{rt}\qquad \begin{cases} A=\textit{accumulated amount}\dotfill & \$ 4700\\ P=\textit{original amount deposited}\\ r=rate\to 4\%\to \frac{4}{100}\dotfill &0.04\\ t=years\dotfill &11 \end{cases} \\\\\\ 4700=Pe^{0.04\cdot 11} \implies 4700=Pe^{0.44}\implies \cfrac{4700}{e^{0.44}}=P\implies 3027\approx P\)
Which term refers to coordination, balance, and orientation in three-dimensional space?
Answers
Equilibrium is the term refers to coordination, balance, and balance in three dimensional space.
The equilibrium condition of an object exists when Newton's first law is valid. An object is in equilibrium in a reference coordinate system when all external forces (including moments) acting on it are balanced. This means that the net result of all the external forces and moments acting on this object is zero.
There are three types of equilibrium: stable, unstable, and neutral.
Examples of equilibrium in everyday life:
A book kept on a table at rest. A car moving with a constant velocity. A chemical reaction where the rates of forward reaction and backward reaction are the same.
Learn more about equilibrium here: https://brainly.com/question/13463225
#SPJ4
Suppose you visit a restaurant with a salad bar containing the following choices: 10
dressings, 15 vegetables, 6 cheese toppings and 4 different crouton toppings. What is
the total number of possible salads you could create?
35
3600
150
900
Answers
Answer:
3600
Step-by-step explanation:
multiply all of the choices
10x15x6x4
The total number of possible salads you could create is 3600. so the correct option is B.
What is the fundamental principle of multiplication?If an event can occur in m different ways and if following it, a second event can occur in n different ways, then the two events in succession can occur in m × n different ways.
WE have been given the following choices: 10 dressings, 15 vegetables, 6 cheese toppings and 4 different crouton toppings.
Therefore, the total number of possible salads you could create;
Then multiply all of the choices
10 x 15 x 6 x 4
= 3600
Hence, The total number of possible salads you could create is 3600. so the correct option is B.
Learn more about multiplications, please visit the link given below;
https://brainly.com/question/14059007
#SPJ2
4:0 Find the point(s) of intersection of the following non-linear system. Include a sketch and label the points of intersection on your sketch. [x² + y² = 16 | 22²-2²2²=1
Answers
The points of intersections of the system of equations are x = ±√(17/2) and y = ±√(15/2)
Finding the points of intersections of the system of equations:From the question, we have the following parameters that can be used in our computation:
x² + y² = 16
x² - y² = 1
Add the equations to eliminate y
So, we have
2x² = 17
Divide both sides by 2
x² = 17/2
Take the square root of both sides
x = ±√(17/2)
Recall that
x² + y² = 16
So, we have
17/2 + y² = 16
This gives
y² = 15/2
Take the square root of both sides
y = ±√(15/2)
Hence, the solutions of the system of equations are x = ±√(17/2) and y = ±√(15/2)
The graph is attached
Read more about equations at
brainly.com/question/13729904
#SPJ1
Question
Find the point(s) of intersection of the following non-linear system. Include a sketch and label the points of intersection on your sketch
x² + y² = 16
x² - y² = 1

Find the missing angle measure of the right triangle. Show all work. Round to the nearest tenth.

Answers
The missing angle measures 139 degrees.
what is triangle?
A triangle is a polygon that has three sides, three angles, and three vertices. It is a two-dimensional figure that is formed by connecting three non-collinear points. The three sides of a triangle can be of different lengths or the same length, and the angles can also vary in size. The sum of the three angles of a triangle always adds up to 180 degrees. Triangles can be classified based on their side lengths and angle measurements.
In a right triangle, the sum of the two acute angles is always equal to 90 degrees. Therefore, we can find the missing angle by subtracting the two given angles from 90 degrees.
Let's call the missing angle "x". Then we have:
x + 21 + 20 = 180 (the sum of angles in any triangle is 180 degrees)
x = 180 - 21 - 20
x = 139 degrees
Therefore, the missing angle measures 139 degrees.
To learn more about triangles from the given link: brainly.com/question/2773823
#SPJ1
What is the measure of each angle foreign by the intersection
Answers
300 degrees
Step-by-step explanation:
identify each term as related to only factorial designs or related to either single independent variable designs or factorial designs. only factorial designs drag appropriate answer(s) here difference in differences press space to open interaction press space to open within-groups design press space to open independent variable press space to open main effect press space to open mixed design
Answers
The appropriate answers are: 1. Difference in differences. 2. Within-groups design. 3. Independent variable. 4. Main effect. 5. Mixed design.
1. Difference in differences: This term is related to both single independent variable designs and factorial designs. It refers to a research design used to estimate the causal effect of a treatment or intervention by comparing the differences in outcomes between a treatment group and a control group before and after the treatment.
2. Within-groups design: This term is related to either single independent variable designs or factorial designs. It refers to a research design where participants are exposed to all levels or conditions of the independent variable(s), and their performance or responses are compared within the same group.
3. Independent variable: This term is related to both single independent variable designs and factorial designs. It refers to the variable(s) manipulated or controlled by the researcher to observe its effect on the dependent variable(s).
4. Main effect: This term is related to factorial designs. It refers to the individual effect of each independent variable in a factorial design on the dependent variable(s), ignoring the interactions between the independent variables.
5. Mixed design: This term is related to factorial designs. It refers to a research design that combines within-groups and between-groups factors, allowing for the examination of both within-subject and between-subject effects in the same experiment.
Learn more about Independent variable here:
https://brainly.com/question/32767945
#SPJ11
how many cup sugar in g?
Answers
As a rough estimate, 100g of sugar is equivalent to 0.5 cups of granulated sugar.
Conversion is the process of changing units of measurement from one system to another.
In this case, we need to convert 100g of sugar into cups. However, the conversion factor for sugar varies depending on factors such as the type of sugar and how densely it is packed. For instance, powdered sugar is denser than granulated sugar, and so the conversion factor will differ.
In general, one cup of granulated sugar weighs around 200g, which means that 100g of sugar is equivalent to 0.5 cups. However, it is essential to note that this conversion factor is approximate and can vary depending on the quality and type of sugar used.
To know more about measurement here.
https://brainly.com/question/4725561
#SPJ4
Complete Question:
how many cup sugar in 100g?
a bag contains 5 red marbles, 6 blue marbles, 10 white marbles and 9 yellow marbles. you are asked to draw 5 marbles from the bag without replacement. what is the probability of drawing 3 or more white marbles?
Answers
the probability of drawing 3 or more white marbles when 5 marbles are drawn from the bag without replacement.
To calculate this probability, we can use the formula for the hypergeometric distribution, which is:
P(X ≥ 3) = [C(10,3) * C(10,2)] / C(30,5) + [C(10,4) * C(10,1)] / C(30,5) + [C(10,5)] / C(30,5)
Where C(n,r) is the number of ways to choose r items from a set of n items.
formula is that we need to consider three different cases: drawing exactly 3 white marbles, drawing exactly 4 white marbles, and drawing all 5 white marbles. For each case, we calculate the probability of drawing the required number of white marbles and the probability of drawing the remaining marbles (non-white marbles), and then multiply them together. Finally, we add up the probabilities for all three cases to get the total probability of drawing 3 or more white marbles.
Using the formula, we get:
P(X ≥ 3) = [(C(10,3) * C(20,2)) + (C(10,4) * C(20,1)) + C(10,5)] / C(30,5)
= [(120 * 190) + (210 * 20) + 252] / 142506
= 0.209
Therefore, the probability of drawing 3 or more white marbles when 5 marbles are drawn from the bag without replacement is 0.209.
using the hypergeometric distribution formula, we can calculate the probability of drawing 3 or more white marbles from a bag containing 5 red marbles, 6 blue marbles, 10 white marbles, and 9 yellow marbles when 5 marbles are drawn without replacement. The probability is 0.209.
To know more about hypergeometric visit:
https://brainly.com/question/30570741
#SPJ11