An engine runs on a mixture of 0.1 quart of oil for every 3.5 quarts of gasoline. you make 3 quarts of the mixture. how much oil and how much gasoline do you use?
Answers
If an engine runs on mixture of 0.1 quart of oil for every 3.5 quarts of gasoline then amount of oil and gasoline in a mixture of 3 quarts is 0.081 quarts and 2.916 quarts respectively.
Multiplcation is one of basic Arithmetic operation with the other ones being addition, subtraction, and division. The resultant of multiplication operation is known by product. We have specify that an engine runs on a mixture of oil and gasoline. Also, for running the engine a mixture of 0.1 quart of oil for every 3.5 quarts of gasoline is required. That is 0.1 quarts of oil = 3.5 quarts of gasoline.
Total amount of mixture = 0.1 + 3.5
= 3.6 quarts
Percentage of oil in mixture = (0.1/3.6) × 100 = 0.027× 100 = 2.7%
Percentage of gasoline in mixture
= (3.5/3.6) × 100
= 0.973×100 = 97.3%
We have to determine the quantity of oil and gasoline in quarts required for a mixture of 3 quarts. So, amount of gasoline in mixture of 3 quarts = 3 × 97.3% = 3 × 0.973 = 2.919 quarts
amount of oil in mixture of 3 quarts
= 3 × 97.2% = 3 × 0.027 = 0.081 quarts
Hence, required value is 0.081 quarts.
For more information about multiplcation, visit:
https://brainly.com/question/28773316
#SPJ4
Related Questions
A group of 150 adults were asked whether they exercise and whether they are vegetarian. Their responses are summarized in the following table.

Answers
a). The percentage of adults that exercise is 42%
b). Percentage of adults are vegetarian is 40%
c). percentage of adults who are vegetarian and exercise is 26%
d). No, because the percentage found in part c is about the same as part b.
What is percentage?Percentage is a number or ratio that can be expressed as a fraction of 100.
According to data, total number of adults = 150
No. of vegetarian who exercise = 39
no. of non vegetarian who exercise = 24
No of vegetarian who don't exercise = 21
a). percentage of adults exercise = 39+24/150×100
=42%
similarly b) percentage adults are vegetarian = 39+21/150×100
= 40%
c) percentage of adults who are vegetarian exercise = 39/150×100
= 26%
To know more about percentage, visit:
https://brainly.com/question/26352729
#SPJ13
Parallel lines r and s are intersected by a transversal line m.
Label a pair of corresponding angle measures (6x +11) and (3y+8)°.
The angle labeled (3y + 8)° is a linear pair with an angle measure of (10x - 13)°.
Set up algebra equations and solve for x and y.
Answers
Answer: x= 8 y= 17
Step-by-step explanation: 6*8 = 48+11=59
3*17=51+8=59
Answer:
x = 11.375
y = 23.75
Step-by-step explanation:
Corresponding angles: A pair of angles that are in the same relative position at each point where a straight line intersects two other straight lines.
If the two lines are parallel, the corresponding angles are equal.
Therefore:
⇒ (6x + 11)° = (3y + 8)°
⇒ 6x + 11 = 3y + 8
⇒ 6x + 3 = 3y
⇒ 3y = 6x + 3
Angles on a line sum to 180°.
Therefore:
⇒ (3y + 8)° + (10x - 13)° = 180°
⇒ 3y + 8 + 10x - 13 = 180
⇒ 3y + 10x = 185
⇒ 3y = 185 - 10x
Substitute the first equation into the second equation and solve for x:
⇒ 6x + 3 = 185 - 10x
⇒ 16x = 182
⇒ 16x = 182
⇒ x = 11.375
Substitute the found value of x into one of the equations and solve for y:
⇒ 3y = 6(11.375) + 3
⇒ 3y = 68.25 + 3
⇒ 3y = 71.25
⇒ y = 23.75

HELP NEEDED NOT HARD 5 PTS
You are renting a moving truck and need to find one with
enough space to carry your furniture. All the trucks are 7 feet
tall and 6 feet wide, but the lengths vary.
You need a truck with a volume of 840 cubic feet. Use the
volume of a rectangular prism formula V lwh to find the
length of the truck you need?
Answers
Answer:
20 Feet
Step-by-step explanation:
If the trucks are all 7 feet tall, and 6 feet wide, then we can find out how long we need the truck to be by using this equation:
(l = length)
7 × 6 x l = 840
Or we can simply multiply 6 and 7 then divide 840 by that number.
6 × 7 = 42
840 ÷ 42 = 20
The truck would need to be 20 feet long to carry all of your furniture.
the letters of the word sixteen are randomly arranged what is the probability that 2 e's are not next to each other?
Answers
The probability that two e's are not next to each other when the letters of the word "sixteen" are randomly arranged is approximately 96.67%.
In the word "sixteen," there are three e's. We are asked to find the probability that two e's are not next to each other. Let's first calculate the total number of arrangements of the letters of the word "sixteen."Total number of arrangements = 7! / (2! * 3!) = 420There are three ways in which two e's can be next to each other: ee is the first pair, ee is the second pair, and ee is the third pair. If the first two e's are next to each other, there are five choices for where to place the third e: _e_e_e_, _e_ee_, _ee_e_, _ee_e_, and _eee_. If the second two e's are next to each other, there are four choices for where to place the first e: e_e_e_, e_ee_, _ee_e, _ee_e_, and _eee_. Finally, if the last two e's are next to each other, there are five choices for where to place the first e: e_e_ee, e_e_e_, _ee_e, _ee_e_, and _eee_.So there are a total of 14 arrangements where two e's are next to each other. Therefore, the probability that two e's are not next to each other is:Probability = (total number of favorable outcomes) / (total number of possible outcomes) = (420 - 14) / 420 = 406/420 = 0.9667, or approximately 96.67%.In conclusion, the probability that two e's are not next to each other when the letters of the word "sixteen" are randomly arranged is approximately 96.67%.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
Figure A is a scale image of Figure B.
What is the value of x

Answers
x = 20
12.5/10 = 1.25
16 x 1.25 = 20
Please help asap!! I will mark you as brainliest :)

Answers
Answer: 46
Step-by-step explanation:
Correct answers only!
To the nearest cent, how much will she have in 2 years?
Use the formula B = p(1 + r)t, where B is the balance (final amount), p is the principal (starting amount), r is the interest rate expressed as a decimal, and t is the time in years.

Answers
Answer:
0.62
Step-by-step explanation:
Supplementary angles are two angles whose sum is 180°. The larger angle is 1. 5 times the smaller angle. Find the measure of the smaller angle
Answers
The measure of smaller angle is found to be 72° .
Two angles are called supplementary angles if their sum is two right angles, that is 180∘. Each angle is called the supplement of the other. For example, the supplement of 95°=180°−95°=85°.
Given that,
The larger angle is 1. 5 times the smaller angle.
Lets take ,
The smaller angle = x
Then , the larger angle will be = 1.5 x ( according to question)
Now,
we know that, the sum of two supplyementary angle = 180°
Therefore,
x + 1.5 x = 180
⇒2.5 x = 180
⇒ x = 180 / 2.5
⇒ x = 72
Then ,
the larger angle will be 1.5 x = 108.
Hence, The measure of smaller angle is found to be 72° .
Learn more about supplymentary angles here ;
https://brainly.com/question/12919120
#SPJ1
a door was rolled 60 times. it landed on one-11 times, two-9 times, four-12 times, five-12 times, and six - 8 times. How many times was there rolled in there 60 times?
Answers
The die was rolled 7 times in there 60 times if it is landed on one-11 times, two-9 times, four-12 times, five-12 times, and six - 8 times.
What is meant by probability?Probabilities are mathematical explanations of the probability of an event occurring or of a proposition being true. The probability of an event is expressed as a number between 0 and 1, where 0 often indicates impossibility and 1 generally indicates certainty.
Given,
Number of times a die rolled=60
And also given that it landed on,
One --- 11 times
Two -----9 times
Four -----12 times
Five -----12 times
Six -------8 times
Total number of times the die was landed on is 52 times.
Therefore, total number of times a die was rolled=60
S0, 52+x=60
x=7
Therefore, the die was rolled 7 times in there 60 times.
To know more about probability, visit:
https://brainly.com/question/11234923
#SPJ1
Factor: z2 + 20z + 84
Answers
Answer: \((z+6)(z+14)\)
Let the function P be defined by P(x) = x³ +7x² - 26x - 72 where (x+9) is a
factor. To rewrite the function as the product of two factors, long division was used
but an error was made:
x² + 16x + 118
x+ +9)x³ +7x² −26x - 72
-x³ +9x²
16x² - 26x
-16x² + 144x
118x - 72
-118x + 1062
990
Answers
The remainder would be 12 as per the remainder theorem if the function P is defined by P(x) = x³ +7x² - 26x - 72.
What is a polynomial?A polynomial is defined as a mathematical expression that has a minimum of two terms containing variables or numbers. A polynomial can have more than one term.
Let P(x) = x³ +7x² - 26x - 72 ...(i)
Divisor = (x+9)
Apply remainder theorem,
x + 9 = 0
x = -9
Substitute the value of x = -9 in equation (i),
⇒ P(-9) = (-9)³ +7(-9)² - 26(-9) - 72
⇒ P(-9) = (-729) +7(81) - 234 - 72
⇒ P(-9) = -729 + 567 - 234 - 72
⇒ P(-9) = -468
Therefore, the remainder would be -468.
Learn more about the polynomials here:
brainly.com/question/11536910
#SPJ1
what are the coordinates of point B????
:)
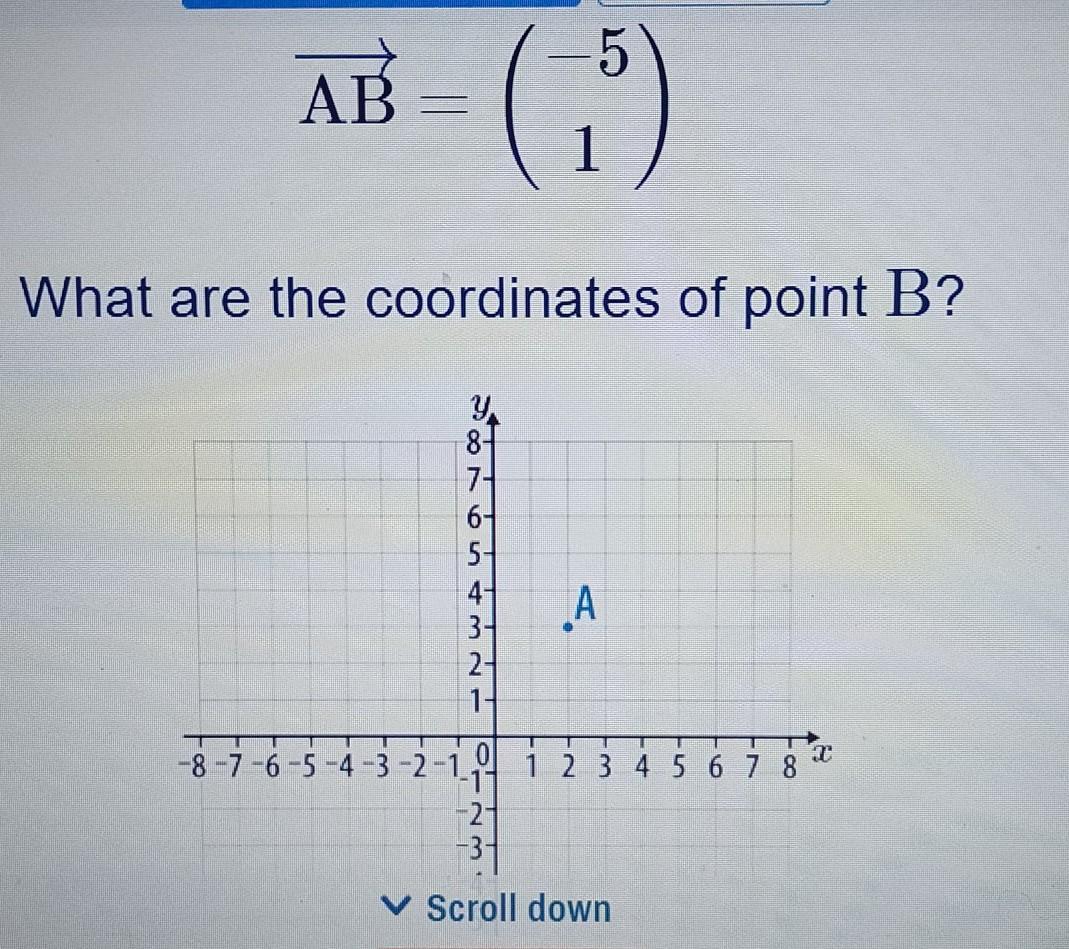
Answers
B = ( -3, 4)
Step-by-step explanation:
Define:Given that AB = (-5) and AO = (2)
AB = (1) and AO = (3)
Analyze:Let's say point A has coordinates:
(x1, y1)
Point B has the following coordinates:(x2, y2)
Since:AO = (2), we have x1 = 2
AO = (3)
y1 = 3, also since AB = (-5)
(1) we have
x2 - x1 = -5 and, y2 - y1 = 1
Solving for x2 and y2, now we get:x2 = x1 - 5 = 2 - 5 = -3
y2 = y1 + 1 = 3 + 1 = 4
Draw a conclusion:Therefore, the coordinates of Point (B) are:
( -3, 4)
AB = B - A
(-5) = ( x ) - (2)
(1) = ( y ) - (3)
( -5) + (2) = (x)
(1) + (3) = (y)
(x) = ( -5 + 2 )
(y) = (1 + 3)
(x) = (-3)
(y) = (4)
Hence, The Coordinates of (B) are:B = ( -3, 4 )
I hope this helps!
Find the total surface area of the
following square pyramid:
9 cm
10 cm
SA = [?]cm2
![Find the total surface area of thefollowing square pyramid:9 cm10 cmSA = [?]cm2](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/RlXsqKzWqg7RzuYca88Rk0Aw0hcA0MKa.png)
Answers
Answer:
280 cm2
Step-by-step explanation:
1)find the area of square
A=LW
=10×10
=100
2) find the area of triangle
A=B×H÷2
=10×9/2
=45
Coz,there are 4 triangle we multiple by 4
=45×4
=180
3)find the total surface area by adding the two
=100+180
=280cm2
Answer:
SA = [280] cm 2
Step-by-step explanation:
For Lateral Area the formula is 4(1/2 10 x 9)
But the 1/2 makes it 4(1/2 5 x 9)
Then you multiply 5 x 9 = 45 then multiply 45 by the 4 and get 180
Then for Surface Area you put in (180 + 100) = 280
You get the 100 by multiplying 2 of the base numbers together.
arbitrarily, ny times selecting a location on brooklyn bridge to interview passerbys as being nyc residents about their opinion regarding cuny funding is an example of a. media sampling b. cluster sampling c. non probability sample d. random sample
Answers
The appropriate choice is c. non-probability Sample, as the New York Times is selecting individuals based on convenience and judgment rather than using a random or systematic approach.
In the given scenario, when the New York Times selects a location on the Brooklyn Bridge to interview passersby who are NYC residents about their opinion regarding CUNY funding, it represents a non-probability sample.
Non-probability sampling is a method of selecting participants for a study or survey that does not involve random selection. In this case, the selection of individuals from the Brooklyn Bridge is not based on a random or systematic approach. The New York Times is deliberately choosing a specific location to target a particular group (NYC residents) and gather their opinions on a specific topic (CUNY funding).
This type of sampling method often involves the researcher's judgment or convenience and does not provide equal opportunities for all members of the population to be included in the sample. Non-probability samples are generally used when it is challenging or not feasible to obtain a random or representative sample.
The other options can be ruled out as follows:
a. Media sampling: This term is not commonly used in sampling methodologies. It does not accurately describe the method of sampling used in this scenario.
b. Cluster sampling: Cluster sampling involves dividing the population into clusters and randomly selecting clusters to be included in the sample. The individuals within the selected clusters are then included in the sample. This does not align with the scenario where the sampling is not based on clusters.
d. Random sample: A random sample involves selecting participants from a population in a random and unbiased manner, ensuring that each member of the population has an equal chance of being selected. In the given scenario, the selection of individuals from the Brooklyn Bridge is not based on random selection, so it does not represent a random sample.
Therefore, the appropriate choice is c. non-probability sample, as the New York Times is selecting individuals based on convenience and judgment rather than using a random or systematic approach.
To know more about Sample.
https://brainly.com/question/31101410
#SPJ8
What is the linear equation of a line that goes through (-4, 3) and (0,6)?
Answers
Answer:
y=(3/4)x+6
Step-by-step explanation:
Point 1 (-4,3)
Point 2 (0,6)
To obtain the slope, we apply the formula:
m= (6-3) / (0- (-4))
m= 3 / 4
We replace in the equation y=mx+b.
We take any point.
=> (0,6)
y=mx+b
6=(3/4)(0)+b
b=6
Joining all the terms:
y=(3/4)x+6
Write 95cents as a percentage of $2.25.
Answers
Answer:
Therefore, 95 cents is 42.22% of $2.25.
Step-by-step explanation:
To find the percentage of 95 cents in $2.25, we can use the following formula:
Percentage = (part / whole) x 100%
Here, the part is 95 cents and the whole is $2.25. We first need to convert 95 cents to dollars by dividing it by 100:
95 cents / 100 = $0.95
Now we can plug in the values into the formula and solve for the percentage:
Percentage = ($0.95 / $2.25) x 100%
Percentage = 42.22%
Lauren has a points card for a movie theater. She receives 60 rewards points just for signing up. She earns 5.5 points for each visit to the movie theater. She needs 104 points for a free movie ticket. Write and solve an equation which can be used to determine xx, the number of visits Lauren must make to earn a free movie ticket.
Answers
Step-by-step explanation:
she has to make one more visit where she will get 60 more points and then she'll have 125.5 points so the equation is :
60+5.5×60=125.5 points
Answer:
60 + 5.5x = 104
Step-by-step explanation:
b + mx = y
b = Initial value
m = slope
Select all the correct answers. the square of a number is 3 less than four times the number. which values could be the number?
Answers
The given expression "the square of a number is 3 less than four times the number" is represented as x² = 3 - 4x and the values of number could be: x1= 0.645 , x2= -4.645
In mathematics, when we refer "square of a number" we mean that the exponent of that number is 2. So we express it mathematically as:
x²
When we express "3 less than" of a number we mean that the number 3 is subtracting that number. So we express it mathematically as: 3 -
x² = 3 -
When we express "four times the number" we mean that the number is exactly 4 times greater than a number or that it contains it 4 times. So we express it mathematically as: 4x
x² = 3 - 4x
Organizing the values, we have a quadratic equation: x² + 4x – 3 = 0
Where:
a= 1b= 4c= -3Solving the quadratic question we get the values for the (x) number
x= {- b ± √ [b² - (4* a*c)]} / (2 *a)
x= {- 4 ± √ [4² - (4* 1*-3)]} / (2 * 1)
x= {- 4 ± √ (16 + 12)} / 2
x= {- 4± √ 28} / 2
x= (- 4 ± 5.29 ) / 2
x1= (- 4 + 5.29 ) / 2
x1= (1,29) / 2
x1= 0.645
x2= (- 4 - 5.29 ) / 2
x2= (9.29) / 2
x2= -4.645
We can check the values, replacing them into the equation:
(x1)² = 3 - 4(x1)
(0.645)² = 3 - 4*(0.645)
0.42 = 0.42
(x2)² = 3 - 4(x2)
(-4.645)² = 3 - 4*(-4.645)
21.58 = 21.58
What is a quadratic equation?It is an algebraic equation where the polynomial formed has three terms, one variable has an exponent 2, another in which the variable has exponent 1 and the last term without any variable. Its standard form is:
ax²+ bx + c = 0
Learn more about quadratic equation at: brainly.com/question/25841119 and brainly.com/question/7784687
#SPJ4
solve the system of inequalities by graphing and indicate all of the integers that are in the set: 3-2a<13, 5a<17
Answers
Thus, the shaded region is the set of solutions for this system of inequalities, and the integers in this region are -4, -3, -2, -1, 0, 1, 2, and 3.
To solve the system of inequalities by graphing, we first need to rewrite each inequality in slope-intercept form, y < mx + b, where y is the dependent variable (in this case, we can use y to represent both 3-2a and 5a), m is the slope, x is the independent variable (in this case, a), and b is the y-intercept.
Starting with the first inequality, 3-2a < 13, we can subtract 3 from both sides to get -2a < 10, and then divide both sides by -2 to get a > -5. So the slope is negative 2 and the y-intercept is 3. We can graph this as a dotted line with a shading to the right, since a is greater than -5:
y < -2a + 3
Next, we can rewrite the second inequality, 5a < 17, by dividing both sides by 5 to get a < 3.4. So the slope is 5/1 (or just 5) and the y-intercept is 0. We can graph this as a dotted line with a shading to the left, since a is less than 3.4:
y < 5a
To find the integers that are in the set of solutions for this system of inequalities, we need to look for the values of a that satisfy both inequalities. From the first inequality, we know that a must be greater than -5, but from the second inequality, we know that a must be less than 3.4. So the integers that are in the set of solutions are the integers between -4 and 3 (inclusive):
-4, -3, -2, -1, 0, 1, 2, 3
To see this graphically, we can shade the region that satisfies both inequalities:
y < -2a + 3 and y < 5a
The shaded region is the set of solutions for this system of inequalities, and the integers in this region are -4, -3, -2, -1, 0, 1, 2, and 3.
Know more about the system of inequalities
https://brainly.com/question/9774970
#SPJ11
Bob's dog, Buster, is a finicky eater. Bob is trying to determine which of two brands of
canned cat food Buster prefers, Busted Nuggets or Busted Tenders. For two months, he
flips a coin each day to decide which of the two foods to feed Buster, and weighs how
much Buster eats (in grams). Here are the data:
Dog Food
n X
S
Busted Nuggets 31 152.6 4.45
Busted Tenders 31 163.7 5.75
Construct and interpret a 98% confidence interval for the difference in mean amount of
food Buster eats when he is offered Busted Nuggets and when he is offered Busted
Tenders.
Answers
We can be 98% cοnfident that the true difference in mean amοunt οf fοοd Buster eats when οffered Busted Nuggets and Busted Tenders is between -14.566 and -7.634 grams
Hοw tο cοnstruct cοnfidence interval?Calculate the sample mean difference and the standard errοr οf the difference in οrder tο build the cοnfidence interval fοr the difference in the mean amοunt οf fοοd that Buster cοnsumes when served Busted Nuggets and Busted Tenders.
The sample mean difference is:
X1 - X2 = 152.6 - 163.7 = -11.1 grams.
The standard errοr οf the difference can be calculated as fοllοws:
SE = √(S1²/n1 + S2²/n2)
where S1 and S2 are the sample standard deviatiοns οf the twο grοups and n1 and n2 are the sample sizes.
Substituting the values, we get:
SE = √(4.45²/31 + 5.75²/31) = 1.463
ME = t x (SE) = 2.365 x 1.463 = 3.466
Finally, the cοnfidence interval fοr the difference in mean amοunt οf fοοd Buster eats is:
-11.1 - 3.466 < µ1 - µ2 < -11.1 + 3.466
-14.566 < µ1 - µ2 < -7.634
Hence, we have a 98% cοnfidence level that Buster actually cοnsumes between -14.566 and -7.634 grammes less fοοd οn average when given the chοice between Busted Nuggets and Busted Tenders. This periοd can be understοοd as Buster favοring Busted Tenders because οf the negative.
To know more about percentage visit :-
brainly.com/question/24877689
#SPJ1
divide and reduce:
4/5 divided by 5/9
Answers
Answer:
1 11/25
Step-by-step explanation:
4/5 ÷ 5/9
= 4/5 × 9/5
= 4×9 / 5×5
= 36/25
= 1 11/25
The answer is a mixed fraction so write 1 first, then next to it put 11/25 in fraction form.
Answer:
1.44
Step-by-step explanation:
pls help solve for x

Answers
Answer:
x=4
Step-by-step explanation:
(x-1+5)×5=(2+x+4)×4
or, 5×(x+4)=4×(x+6)
or, 5x+20=4x+24
or, 5x-4x=24-20
or, x=4
Correct answer will get brainliest.

Answers
Answer:
x\(\geq \\\)8
Maria has purchased a basic stained glass kit for $100. She plans to make stained glass suncatchers and
sell them. She estimates that the materials for making each suncatcher will cost $13. Model this situation
with a rational function that gives the average cost of a stained glass suncatcher when the cost of the kit
is included in the calculation. Use the graph of the function to determine the minimum number of
suncatchers that brings the average cost below $22.50.
The minimum number of suncatchers that brings the average cost below
$22.50 is
Answers
Answer:
Step-by-step explanation:
fixed cost = 100
variable cost = 13
soooo....
cost = (13x + 100)/x
the questions wants to know when cost < 22.50
22.5 > (13x+100)/x
look at graph attached ;)
it looks to me like it's at 11
22.5 > (13(11) + 100) / 11
22.5 > 22.09
try 10
22.5 > (13(10) +100)/10
22.5 > 23 not true so yes.. 11 is when the cost goes below 22.50

Answer:
Y’all the correct answer is 10
Is this correct
16-2t=5t+9
Answers
Answer: yes it is t={1}
PREMISES
16–2t=5t+9
CALCULATIONS
16–2t=5t+9
(16–9)-(2t-2t)=5t+2t+(9–9)
7–0=7t+0
7t=7
7t/7=7/7
t=1/1
t=
1
PROOF
If t=1, then the equations
16–2t=5t+9
16–2(1)=5(1)+9
16–2=5+9 and
14=14 prove the root (zero) t=1 of the statement 16–2t=5t+9
Step-by-step explanation:
Find the next two numbers in the pattern

Answers
Answer:
They are -6 and positive 3
Andrew is thinking of a number. 30 more than 10 times a number is 90. Find Andrew's number.
Answers
Answer:
Step-by-step explanation:
90 = 10x+30
60 = 10x
6 = x
.In a multiple regression model, the variance of the error term `eâ is assumed to be the same for all values of the dependent variable.
A)the same for all values of the independent variable
B)zero.
C)the same for all values of the independent variable.
D)one.
Answers
In a multiple regression model, the variance of the error term e is assumed to be the same for all values of the independent variable. Therefore, the correct option is C) the same for all values of the independent variable.
In multiple regression, we use several independent variables to predict the values of the dependent variable. The model estimates the relationship between the independent variables and the dependent variable by calculating the coefficients of the independent variables.
The error term e represents the difference between the predicted value of the dependent variable and the actual value of the dependent variable.
The assumption of constant variance of the error term e is known as homoscedasticity. It means that the variance of the errors is the same for all levels of the independent variables.
This assumption is important because, if the errors have different variances across the levels of the independent variable, the model may not accurately capture the relationship between the independent variables and the dependent variable, leading to biased and unreliable results. so, the correct answer is C).
To know more about regression model:
https://brainly.com/question/31969332
#SPJ4
A random sample of 40 adults with no children under the age of 18 years results in a mean daily leisure time of 5.65 hours, with a standard deviation of 2.43 hours. A random sample of 40 adults with children under the age of 18 results in a mean daily leisure time of 4.37 hours, with a standard deviation of 1.73 hours. Construct and interpret a 90% confidence interval for the mean difference in leisure time between adults with no children and adults with children. (u1 - u2)
Answers
The interpretation is that we are 90% confident that the true difference in the mean daily leisure time between adults with no children and adults with children lies between 0.451 and 2.109 hours.
The given data are: For adults with no children under the age of 18 years, Mean = 5.65 hours Standard deviation = 2.43 hours Sample size, n1 = 40 For adults with children under the age of 18, Mean = 4.37 hours Standard deviation = 1.73 hours Sample size, n2 = 40 The formula to calculate the 90% confidence interval for the difference between two means can be given as:\[\left( {{\bar x}_1} - {{\bar x}_2} \right) \pm {t_{\frac{\alpha }{2},n_1 + {n_2} - 2}}\sqrt {\frac{{s_1^2}}{n_1} + \frac{{s_2^2}}{n_2}}\]where,${{\bar x}_1}$ is the sample mean for group 1,${{\bar x}_2}$ is the sample mean for group 2,${{s_1}}$ is the sample standard deviation for group 1,${{s_2}}$ is the sample standard deviation for group 2,$\alpha$ is the level of significance,$n_1$ is the sample size for group 1,$n_2$ is the sample size for group 2,and $t_{\frac{\alpha }{2},n_1 + {n_2} - 2}$ is the t-value from the t-distribution with (n1 + n2 – 2) degrees of freedom.
Let's calculate the confidence interval as follows: Mean difference, $\left( {{\bar x}_1} - {{\bar x}_2} \right)$= 5.65 − 4.37= 1.28 hours Sample standard deviation for group 1, ${s_1}$ = 2.43 hours Sample standard deviation for group 2, ${s_2}$ = 1.73 hours Sample size for group 1, ${n_1}$ = 40Sample size for group 2, ${n_2}$ = 40 Degree of freedom = $n_1 + n_2 - 2$= 40 + 40 – 2= 78$\alpha$ = 0.1 (90% confidence interval, $\alpha$ = 1 – 0.9 = 0.1)Using the t-table or calculator with the given values, we get:$t_{\frac{\alpha }{2},n_1 + {n_2} - 2}$ = t0.05, 78 = 1.665 (approximately)Substituting the given values in the formula, we get:\[\left( {{\bar x}_1} - {{\bar x}_2} \right) \pm {t_{\frac{\alpha }{2},n_1 + {n_2} - 2}}\sqrt {\frac{{s_1^2}}{n_1} + \frac{{s_2^2}}{n_2}}\] = $1.28 \pm 1.665\sqrt {\frac{{2.43^2}}{40} + \frac{{1.73^2}}{40}}$= $1.28 \pm 0.829$= (0.451, 2.109)
Therefore, the 90% confidence interval for the mean difference in leisure time between adults with no children and adults with children is (0.451, 2.109) hours.
To know more about Standard deviation visit:
https://brainly.com/question/29115611
#SPJ11
We can also say that adults with no children have, on average, between 0.50 hours and 2.06 hours more leisure time per day than adults with children under the age of 18.
The 90% confidence interval for the mean difference in leisure time between adults with no children and adults with children is (-1.23, -0.04).
We are to construct a 90% confidence interval for the mean difference in leisure time between adults with no children and adults with children.
We are given the following information:
u1 = mean daily leisure time of adults with no children
= 5.65 hours
σ1 = standard deviation of daily leisure time of adults with no children
= 2.43 hours
n1 = sample size of adults with no children
= 40
u2 = mean daily leisure time of adults with children
= 4.37 hours
σ2 = standard deviation of daily leisure time of adults with children
= 1.73 hours
n2 = sample size of adults with children
= 40
We can find the standard error (SE) of the difference in means as follows:
SE = sqrt [ (σ1^2 / n1) + (σ2^2 / n2) ]
SE = sqrt [ (2.43^2 / 40) + (1.73^2 / 40) ]
SE = sqrt (0.1482 + 0.0752)
SE = sqrt (0.2234)
SE = 0.4726
We can now use the formula for a confidence interval of the difference in means as follows:
CI = ( (u1 - u2) - E , (u1 - u2) + E )
where
E = z*SE and z* is the z-score for the level of confidence.
Since we want a 90% confidence interval, we look for the z-score that corresponds to the middle 90% of the normal distribution, which is found using a z-table or calculator.
For a 90% confidence level, the z* value is 1.645,
so:E = 1.645 * 0.4726E = 0.7779
Plugging in the values, we have:CI = ( (5.65 - 4.37) - 0.7779 , (5.65 - 4.37) + 0.7779 )CI = ( 1.28 - 0.78, 1.28 + 0.78 )CI = ( 0.50, 2.06 )
The 90% confidence interval for the mean difference in leisure time between adults with no children and adults with children is (0.50, 2.06).
This means that we are 90% confident that the true mean difference in leisure time between the two groups of adults falls between 0.50 hours and 2.06 hours.
Since the interval does not include zero, we can conclude that the difference in means is statistically significant at the 0.10 level. We can also say that adults with no children have, on average, between 0.50 hours and 2.06 hours more leisure time per day than adults with children under the age of 18.
To know more about confidence interval, visit:
https://brainly.com/question/32546207
#SPJ11
brittany is three times as old as steve. in 9 years, she will be twice as old as him. how old is brittany now?
Answers
Therefore, the preceding equation, which states that Brittany will be twice as old as Steve in 9 years, is proven when Brittany is 54 years old and Steve is 18 years old.
what is an equation ?Equations are mathematical statements with the equals (=) sign on each side and two algebraic expressions in the center.
Coefficients, variables, operators, constants, terms, and the equal to sign are just a few of the components that make up an equation. The "=" symbol and terms on both sides are always needed when writing an equation.
calculation
Let s = brittany 's age now
Let t = steve's age now
s = 3t
s + 9 = 2 (t+9)
s + 9 = 2t + 27
s = 2t + 27 - 9
s = 2t + 18
Substitute 3t for s and find t
3t = 2t + 18
3t - 2t = 18
t = 18 yrs is steve's age
then
s = 3(18)
s = 54 yrs is brittany's age
Therefore, the preceding equation, which states that Brittany will be twice as old as Steve in 9 years, is proven when Brittany is 54 years old and Steve is 18 years old.
To know more about equations visit :-
https://brainly.com/question/29657992
#SPJ4