Ankur estimated the quotient of 15 and one-third divided by (negative 4 and two-thirds) to be 3. Which best describes his error?
Answers
Answer:
When dividing a positive number by a negative number, the result is negative.
So the answer would be -3.
I hope this helps
Related Questions
please help!!!!!
6 wholes and 1/2—1 wholes and 1/3=
Answers
The value of 6½ - 1⅓ is 5 ⅙
What are fractions?A fraction is a part of a whole. In arithmetic, the number is expressed as a quotient, in which the numerator is divided by the denominator. In a simple fraction, both are integers. A complex fraction has a fraction in the numerator or denominator. In a proper fraction, the numerator is less than the denominator.
To solve 6½ - 1⅓ ;
we make the mixed fraction improper fraction
= 13/2 - 4/3
= (39-8)/6
= 31/6
= 5 1/6
therefore The value of 6½ - 1⅓ = 5 1/6
learn more about fractions from
https://brainly.com/question/78672
#SPJ1
Step-by-step explanation:
\(6 \frac{1}{2} - 1\frac{1}{3} = 5 \frac{1}{6} \)
Your family ate at a diner and left a 15% tip that was
$7.35. How much was the bill?
Answers
Answer: $49 w/o tip
Step-by-step explanation:
15% of the total = 7.35
10% of the total = 2/3 of 7.35
10% of the total = 4.9
100% of the total = 49
THE BILL WAS $49, AND WITH THE TIP $56.35
Answer:
the bill was $17.00
Step-by-step explanation:
Your family ate at a diner and left a 15% tip that was
$7.35. How much was the bill?
solve for x. someone pls help lol i’m marking brzinliest!!!!
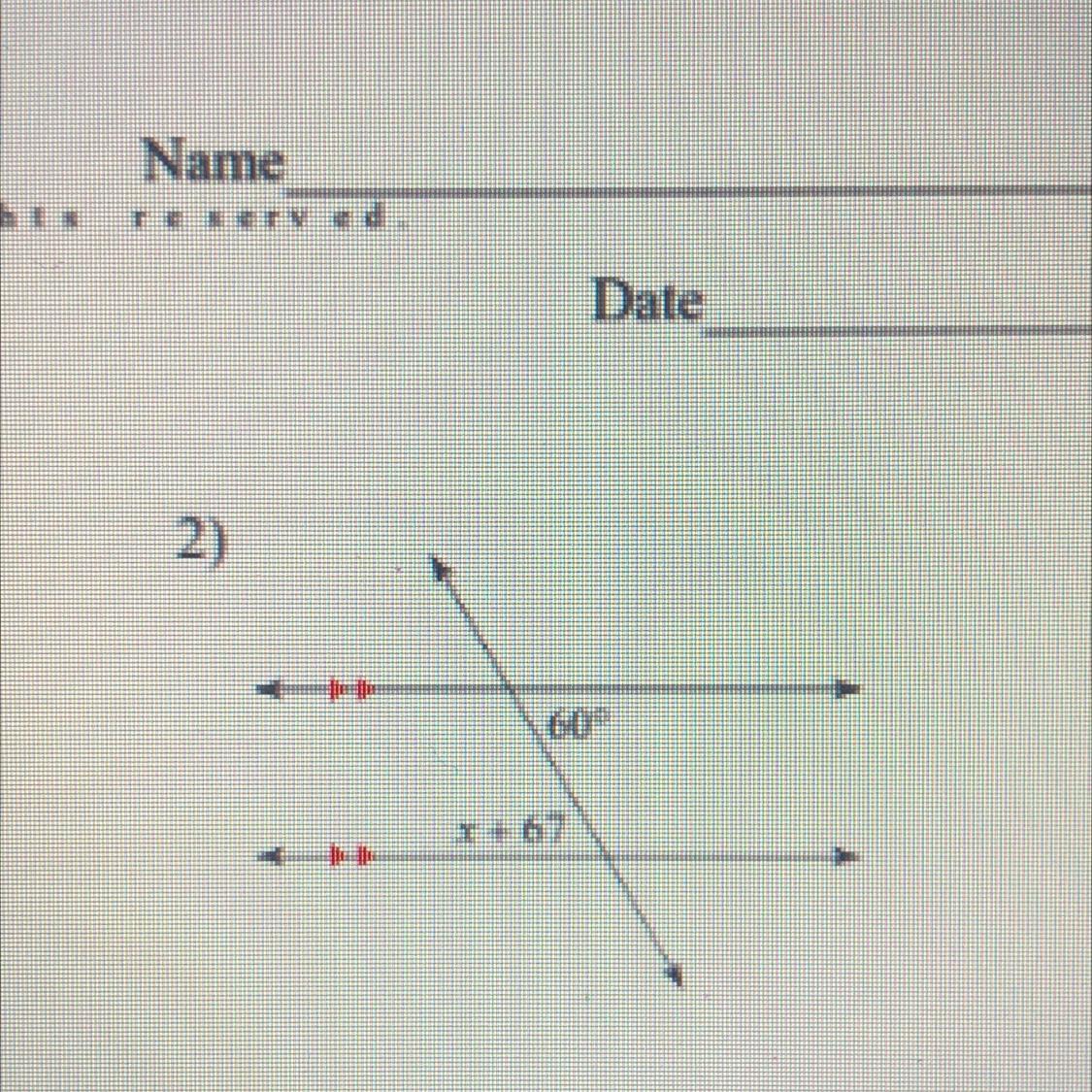
Answers
Answer:
x= 7
Step-by-step explanation:
I got 7 by subtracting 67-7 and i got 60 so x equals 7
1. DIRECTIONS: Write YES if the tatement i correct and NO if not and explain why it i incorrect. 24 i a multiple of 4
6 i a factor of 3
5 i a factor of 35
100 i a multiple of 5
pakiagot po pl
Answers
The solution for the given statements are,
1. YES
2. NO
3. YES
4. YES
Given statements,
We have to show whether its YES or NO,
1. 24 is a multiple of 4
→ YES, 24 is a multiple of 4 as [4 * 6 = 24]
2. 6 is a factor of 3
→ NO, 6 is not a factor of 3 but it is a multiple of 3.
3. 5 is a factor of 35
→YES, 5 is a factor of 35 as 35 factors are 1, 5, 7, and 35.
4. 100 is a multiple of 5
→YES, 100 is a multiple of 5 as [5 * 20 = 100]
Hence, these are given statements answers.
To learn more about factor click here:
brainly.com/question/26923098
#SPJ4
What is the value of y in the equation 3/4(2y + 4) = 30 ?
Answers
2y + 4 = 40
2y = 36
y= 18
Only need answer A answered please

Answers
HEY MATE HERE IS UR ANSWER
The graph of the function is the set of all points (x,y) in the plane that satisfies the equation y=f(x) y = f ( x ) . ... A vertical line includes all points with a particular x value. The y value of a point where a vertical line intersects a graph represents an output for that input x value.
FOLLOW ME AND MARK AS BRAINLIEST AND CHAT INBOX
40 + 3 = 15
HELPpppp
Answers
Step-by-step explanation:
uhm how do i help?
Answer:
umm the answer is actually 43...
Bus A travels according to the function y = 125 /2 x where y is distance traveled in miles and x is time in hours. Bus B travels according to the graph below, where the distance y is a function of time x . Which bus travels faster? Include all necessary calculations in your final answer.
Answers
Answer:
Bus B travels faster.
Step-by-step explanation:
The graph of the question in the attached figure
we know that
the linear equation in slope intercept form is equal to
where
m is the slope
b is the y-intercept
x ---> is the time in hours
y ---> is the distance in miles
In this problem we have
Bus A
The slope of the linear equation represent the speed of the bus
so
The speed of bus A is
Bus B
Find the slope
take two points from the graph
(0,0) and (3,200)
The formula to calculate the slope between two points is equal to
substitute
Compare the slope Bus A with the slope Bus B
therefore
Bus B travels faster.
How do you determine if something is a factor of a function?.
Answers
if the function is divided and we get the remainder of zero then it is said to be a factor of a function
According to the Remainder Theorem, by a factor x − an of that polynomial, then you will get a zero remainder. The point of the Factor Theorem is the turnaround of the Remainder Theorem: On the off chance that you synthetic-divide a polynomial by x = a and get a zero remainder, at that point not as it were is x = a, a zero of the polynomial(for the remainder theorem ) but x − a is additionally a factor of the polynomial according to of the Factor Theorem.
to know more remainder refer to the link https://brainly.com/question/23148931?referrer=searchResults.
#SPJ4
A company’s stock opened at 68 3/8 dollars per share. The stock dropped 1 7/8 dollars on Monday. The stock dropped another 2 1/2 dollars on Tuesday. On Wednesday, the stock gained back 4 1/4 dollars. brainly
Answers
Answer:
273/4
Step-by-step explanation:
We know
A company’s stock opened at 68 3/8 dollars per share
68 3/8 = 547/8
The stock dropped 1 7/8 dollars on Monday
1 7/8 = 15/8
547/8 - 15/8 = 532/8
The stock dropped another 2 1/2 dollars on Tuesday.
2 1/2 = 5/2
532/8 - 5/2 = 532/8 - 20/8 = 512/8
On Wednesday, the stock gained back 4 1/4 dollars.
4 1/4 = 17/4
512/8 + 17/4 = 512/8 + 34/8 = 546/8
546/8 = 273/4
So, the answer is 273/4
first foot forward: a two-step econometric method for parsing and estimating the impacts of multiple identities
Answers
The "First Foot Forward" method is a two-step econometric approach that involves categorizing multiple identities and estimating their impacts on economic factors. By employing this method, researchers can gain insights into how different identities shape economic outcomes and develop a deeper understanding of the complex interplay between identities and economic systems.
The "First Foot Forward" method is an econometric approach that aims to parse and estimate the impacts of multiple identities on economic factors or outcomes. In this context, identities refer to characteristics or attributes that individuals possess, such as gender, race, age, education level, or socioeconomic status. These identities can significantly shape individuals' experiences, opportunities, and outcomes within economic systems.
1. Identity Categorization: The first step is to identify and categorize the different identities that are relevant to the research question or analysis. This may involve gathering data on various individual characteristics or using existing classification systems. By categorizing identities, researchers can better understand the diverse factors that influence economic outcomes.
2. Estimation of Impacts: The second step involves estimating the individual impacts of these identities on the desired economic factors or outcomes. This is typically done using econometric modeling techniques, such as regression analysis. Researchers analyze how different identities, either individually or in combination, affect specific economic variables of interest, such as income, employment, educational attainment, or consumption patterns. By estimating these impacts, the method aims to provide insights into how multiple identities interact and influence economic outcomes.
The "First Foot Forward" method offers a systematic and structured approach to understanding the complex relationships between multiple identities and economic factors. It recognizes that individuals' experiences and outcomes are shaped by various identity-related factors, and by analyzing these factors separately and collectively, researchers can gain a more nuanced understanding of the underlying dynamics.
This method is particularly useful in areas such as labor economics, social policy, and inequality studies, where the influence of multiple identities on economic outcomes is of significant interest. By employing econometric techniques, researchers can quantify the relative importance of different identities and their impacts on economic factors, helping to inform policy decisions and interventions aimed at reducing disparities and promoting equitable economic outcomes.
To know more about First Foot Forward refer here
https://brainly.com/question/32372164#
#SPJ11
2. How many solutions does the system of equations have? (A no solution B exactly one solution c exactly two solutions D infinitely many solutions
Answers
The number of solutions of the system of equations is given as follows:
D. Infinitely many solutions.
How to obtain the number of solutions of the system of equations?The system of equations is defined as follows:
4x - 9y = 1.12x - 27y = 3.The second equation was obtained multiplying the first equation by 3, meaning that the two equations are multiples, and thus the system of equations has an infinity number of solutions and the correct option is given by option D.
Missing InformationThe system of equations is defined as follows:
4x - 9y = 1.12x - 27y = 3.More can be learned about a system of equations at https://brainly.com/question/30374328
#SPJ1
On average, 4 customers per hour use the public telephone in the sheriff's detention area, and this use has a Poisson distribution. The length of a phone call varies according to a negative exponential distribution. with a mean of 5 minutes. The sheriff will install a second telephone booth when an arrival can expect to wait 3 minutes or longer for the phone
a. By how much must the arrival rate per hour increase to justify a second telephone booth?
b. Suppose the criterion for justifying a second booth is changed to the following: install a second booth when the probability of having to wait at all exceeds 0.6 Under this criterion, by how much must the arrival rate per hour increase to justity a second booth?
Answers
A. The arrival rate per hour must increase to at least 10 customers per hour to justify a second telephone boothe.
B. The arrival rate per hour must increase by at least 1.6 customers per hour to justify a second telephone booth under the new criterion.
How to calculate arrival rateTo get the how much arrival rate must increase, we must get the expected waiting time for a customer.
Assuming;
X is the number of customers who arrive per hour
Y is the length of a phone call in minutes.
Then, X follows a Poisson distribution with λ = 4 (since 4 customers per hour use the phone on average)
Y follows a negative exponential distribution with mean μ = 5 (since the mean length of a phone call is 5 minutes).
Total time is given as sum of waiting time and length of call;
T = W + Y
The waiting time W is the difference between the time a customer arrives and the time that the phone becomes available. waiting time follows a uniform distribution where mean= 1/λ (since the arrivals follow a Poisson process);
Then we have;
E(W) = 1/(2λ) = 1/8 hours
The expected total time T that a customer spends at the phone booth is:
E(T) = E(W) + E(Y) = 1/8 + 5/60 = 11/48 hours
For a second telephone booth to be justifiable, new customer that arrives must wait 3 minutes or longer for the phone.
E(W) ≥ 1/20
To get λ,
1/(2λ) ≥ 1/20
λ ≤ 10
This means that, the arrival rate per hour must increase to at least 10 customers per hour to justify a second telephone booth.
b. Getting how much the arrival rate per hour must increase to justify a second telephone booth under the new criterion,
we need to find the probability that a customer has to wait at all.
Let P(W > 0) be the probability that a customer has to wait.
P(W > 0) = 1 - P(W = 0)
The waiting time W follows a uniform distribution with mean 1/λ, so we have:
P(W = 0) = 1 - λ/4
The length of a phone call Y follows a negative exponential distribution with mean 5 minutes = 1/12 hours, so we have:
P(Y > t) = e^(-μt) = e^(-t/12)
The probability that a customer has to wait is given as;
P(W > 0) = 1 - P(W = 0) = λ/4
To justify a second telephone booth, the probability of having to wait at all must exceed 0.6. so we have;
P(W > 0) > 0.6
λ > 2.4
The arrival rate per hour must increase by at least 2.4 - 4 = 1.6 customers per hour to justify a second telephone booth under the new criterion.
Learn more on Probability on https://brainly.com/question/25870256
#SPJ4
a population consists of the following five values: 2, 4, 6, 6, and 8. a. list all samples of size 2 from left to right, and compute the mean of each sample. (round your mean value to 1 decimal place.)
Answers
The means of the 10 possible samples of size 2 from the population {2, 4, 6, 6, 8} are 3, 4, 4, 5, 5, 5, 6, 6, 7, and 7.
To list all possible samples of size 2 from the given population of 5 values, we can use combinations. The possible combinations of two values from a set of five are:
{2, 4}, {2, 6}, {2, 6}, {2, 8}, {4, 6}, {4, 6}, {4, 8}, {6, 6}, {6, 8}, {6, 8}
To compute the mean of each sample, we add the two values in the sample and divide by 2. The mean of each sample, rounded to 1 decimal place, is:
{2, 4}: (2 + 4)/2 = 3
{2, 6}: (2 + 6)/2 = 4
{2, 6}: (2 + 6)/2 = 4
{2, 8}: (2 + 8)/2 = 5
{4, 6}: (4 + 6)/2 = 5
{4, 6}: (4 + 6)/2 = 5
{4, 8}: (4 + 8)/2 = 6
{6, 6}: (6 + 6)/2 = 6
{6, 8}: (6 + 8)/2 = 7
{6, 8}: (6 + 8)/2 = 7
Therefore, the means of the 10 possible samples of size 2 from the population {2, 4, 6, 6, 8} are 3, 4, 4, 5, 5, 5, 6, 6, 7, and 7.
Learn more about population here
https://brainly.com/question/29885712
#SPJ11
Terry is filling spherical water balloons with a faucet that puts out 100 cm 3 100 cm 3 100, start text, space, c, m, end text, cubed of water per second. At that rate, it takes Terry 6 66 seconds to fill a balloon. What is the radius of a filled balloon?
Answers
Correct question is;
Terry is filling spherical water balloons with a faucet that puts out 100 cm³ of water per second. At that rate, it takes Terry 6 seconds to fill a balloon. What is the radius of a filled balloon?
Answer:
r = 5 cm
Step-by-step explanation:
Volume of a sphere is;
V = (4/3)πr³
It takes 6 seconds to fill the balloon when a faucet that puts out 100 cm³ of water per second.
Thus,
Volume of balloon = 100 × 6 = 600 cm³
Thus;
(4/3)πr³ = 600
r³ = (600 × 3)/4π
r³ = 143.239
r = ∛143.239
r = 5.23
Approximation to the nearest whole number gives; r = 5 cm
–1+–10+–10–5z
answer
now
please-
Answers
Answer:
−5z−21
Step-by-step explanation:
If factored it is :-5z-21
Answer:
-21-5z
Step-by-step explanation:
-1+(-10)+(-10)-5z
-1-10-10-5z
-1-20-5z
-21-5z
Simplify the expression:
-3(3-4x) =
Answers
Answer:
- 9 + 12x
Step-by-step explanation:
- 3(3 - 4x) ← multiply each term in the parenthesis by - 3
= - 9 + 12x
Let X be a continuous random variable with PDF:
fx(x) = \begin{Bmatrix} 4x^{^{3}} & 0 < x \leq 1\\ 0 & otherwise \end{Bmatrix}
If Y = 1/X, find the PDF of Y.
If Y = 1/X, find the PDF of Y.
Answers
Since Y = 1/X, then X = 1/Y. The PDF of Y, g(y) is 4/y⁵, where 0 < y ≤ 1. If Y < 0 or y > 1, the PDF of Y is equal to z of Y, g(y) is 4/y⁵, where 0 < y ≤ 1. If Y < 0 or y > 1, the PDF of Y is equal to zero.
The PDF of X is given by fx(x) = { 4x³, 0 < x ≤ 1}When 0 < Y ≤ 1, the values of X would be 1/Y < x ≤ ∞ .Thus, the PDF of Y, g(y) would be g(y) = fx(1/y) × |dy/dx| where;dy/dx = -1/y², y < 0 (since X ≤ 1, then 1/X > 1). The absolute value is used since the derivative of Y with respect to X is negative. Note that;g(y) = 4[(1/y)³] |-(1/y²)|g(y) = 4/y⁵ , 0 < y ≤ 1. The PDF of Y is 4/y⁵, where 0 < y ≤ 1. When Y < 0 or y > 1, the PDF of Y is equal to zero. The above can be verified by integrating the PDF of Y from 0 to 1.
∫ g(y) dy = ∫ 4/y⁵ dy, from 0 to 1∫ g(y) dy = (-4/y⁴) / 4, from 0 to 1∫ g(y) dy = -1/[(1/y⁴) - 1], from 0 to 1∫ g(y) dy = -1/[(1/1⁴) - 1] - (-1/[(1/0⁴) - 1])∫ g(y) dy = -1/[1 - 1] - (-1/[(1/0) - 1])∫ g(y) dy = 1 + 1 = 2. From the above, it can be observed that the integral of g(y) is equal to 2, which confirms that the PDF of Y is valid. The PDF of Y, g(y) is 4/y⁵, where 0 < y ≤ 1. If Y < 0 or y > 1, the PDF of Y is equal to zero.
To know more about derivative visit:
brainly.com/question/29144258
#SPJ11
Solve each equation for the given variable. m/F = 1/a ; F
Answers
To solve the equation m/F = 1/a for F, we can rearrange the equation as F = a/m.
To solve for a specific variable in an equation, we isolate that variable on one side of the equation. In this case, we want to solve for F when given the equation m/F = 1/a. To do this, we need to isolate F.
We can start by cross-multiplying the equation to eliminate the fractions. Multiply both sides of the equation by F and a to obtain ma = F. Then, we can rearrange the equation to solve for F by dividing both sides by m, resulting in F = a/m.
This means that F is equal to the ratio of a divided by m. By rearranging the equation in this way, we have isolated F on one side and expressed it in terms of the given variables a and m.
In summary, to solve the equation m/F = 1/a for F, we rearrange the equation as F = a/m. This allows us to express F in terms of the given variables a and m.
Learn more about Equation
brainly.com/question/29538993
brainly.com/question/29657983
#SPJ11
PLEASE HELP!!!!!! Write and solve the inequality.
Six more than the quotient of a number b and 30 is greater than 4.
Fill in the boxes.
+6V 4
30
-2
30
b

Answers
Answer:
\(\orange{ \rule{40pt}{555555pt}}\)
What one for question 9 I have been stuck on this one

Answers
Answer:
d \(\geq \\\)-39
Step-by-step explanation:
d/13\(\geq \\\)-3
multiply both sides by 13
d \(\geq\) 13(-3)
d \(\geq\) -39
hope this helps
help pleaseee its timed thank you

Answers
Answer:
It's the first one
Step-by-step explanation:
If a mechanic uses his credit card to pay for a compressor that costs $477.95 and does not pay on it until the second month, what will the 1.5% monthly interest charge be at the end of the first month?
Answers
Answer:
my dads a mechanic too
Step-by-step explanation:
bc i live with him so ik
Answer: $7.17
Hope this helps :)
Find the sum (7x + 2) + (-8x + 5).
ur supposed to like simplify it btw its for my sister
Answers
Answer:
-x+7
Step-by-step explanation:
(7x + 2) + (-8x + 5)
Combine like terms
7x -8x +2+5
-x +7
Answer:
-x + 7. It's honestly quite easy if you just try, I have a recommendation for you. Use an algebra solver website
Listen What is the volume in cubic inches of a box that is 25 cm by 25 cm by 25 cm (given
1 inch = 2.5 cm approx.) A
Answers
The volume of the box is 1000 cubic inches. False, the government does not ensure that you always get paid in international transportation; payment is determined by contracts and agreements between parties.
3: To find the volume of the box in cubic inches, we need to convert the dimensions from centimeters to inches. Given that 1 inch is approximately equal to 2.5 cm, we can calculate the volume as follows:
Length in inches = 25 cm / 2.5 cm/inch = 10 inches
Width in inches = 25 cm / 2.5 cm/inch = 10 inches
Height in inches = 25 cm / 2.5 cm/inch = 10 inches
Volume = Length × Width × Height = 10 inches × 10 inches × 10 inches = 1000 cubic inches
Therefore, the volume of the box is 1000 cubic inches.
5: The statement "International transportation is regulated by the government which ensures that you always get paid" is false. International agencies (such the International Maritime Organization and the International Civil Aviation Organization) as well as standards set by the private sector all have a role in regulating international transportation.
The government plays a role in regulating certain aspects of international transportation, but it does not ensure that you always get paid. Payment and financial matters are typically governed by contracts and business agreements between parties involved in international transportation.
To know more about International transportation refer here :
https://brainly.com/question/33497113#
#SPJ11
Complete question :
Question 3 (1 point) Listen What is the volume in cubic inches of a box that is 25 cm by 25 cm by 25 cm (given 1 inch = 2.5 cm approx.) AY Question 5 (1 point) Listen International transportation is regulated by the government which ensures that you always get paid True False
7. A survey of 15 females on a day of vaccination I on a certain day were as follows: 22 OPM1501/102/0/2022 25;74;78;57;36;43;57;89;56;91;43;33;61;67;52. Use this information to answer questions 7.1. to 7.3. 7.1 the modal age (2) a) 57 and 43 b) 20 c) 57 d) 43 7.2 the median of the above data is (2) a) 57 b) 57+57 c) 56 d) 89 7.3 the mean age of the females vaccinated. a) 862 b) 57 c) 57.47 d) 59 8. Calculate the area of a trapezium that has parallel sides of 9 cm and 12 cm respectively and the perpendicular distance of 7 cm between the parallel sides. (5) a) 73.5 cm
2
b) 73.5 cm c) 756 cm
2
d) 378 cm
2
9. The average mass of 50 pumpkins is 2,1 kg. If three more pumpkin are added, the average mass is 2,2 kg. What is the mass of the extra pumpkins? (5) a) 7.2 kg b) 11.6 kg c) 0.1 kg d) 3.87 kg
Answers
7.1 The age that appears most frequently is 57, and it also appears twice. Therefore, the answer is (a) 57 and 43.
7.2 There are 15 ages, so the middle value(s) would be the median. In this case, there are two middle values: 56 and 57. Since there are two values, the median is the average of these two numbers, which is 56 + 57 = 113, divided by 2, resulting in 56.5.
Therefore, the answer is (c) 56.
7.3 The answer is (c) 57.47.
8. Given: a = 9 cm, b = 12 cm, and h = 7 cm. Substituting these values into the formula, we get (9 + 12) 7 / 2 = 21 7 / 2 = 147 / 2 = 73.5 cm².
Therefore, the answer is (a) 73.5 cm².
9. Let's denote the total mass of the 50 pumpkins as M. We know that the average mass of 50 pumpkins is 2.1 kg.
Therefore, the sum of the masses of the 50 pumpkins is 50 2.1 = 105 kg.
If three more pumpkins are added, the total number of pumpkins becomes 50 + 3 = 53. The average mass of these 53 pumpkins is 2.2 kg. The total mass of the 53 pumpkins is 53 2.2 = 116.6 kg.
Therefore, the answer is (b) 11.6 kg.
Learn more about Value here:
https://brainly.com/question/30145972
#SPJ11
a scientist mixes water (containing no salt) with a solution that contains 30% salt. she wants to obtain 210 ounces of a mixture that is 5% salt. how many ounces of water and how many ounces of the 30% salt solution should she use?
Answers
Answer:
er n4356463
Step-by-step explanation:
I need help I have a lot of work

Answers
1. 20
2. 60
3. 120
2) 60
3) 120
Hope you complete all of your work on time :)
At a local print shop, 4 copies can be made for $2. At this rate, how much would it cost to make 28 copies?
Answers
Answer:
it would cost 14 dollars
Step-by-step explanation:
Use integral tables to evaluate.
∫ 3/ 2x √( 9x^2−1) dx; x > 1/3
Answers
The evaluated integral is \($\frac{1}{2}\ln|3x + \sqrt{9x^2 - 1}| + C$\), where \($C$\) represents the constant of integration.
To evaluate the integral \($\int \frac{1}{x \sqrt{9x^2 - 1}}\,dx$\), we can use integral tables and trigonometric substitutions. Let's start by making a trigonometric substitution: let \($3x = \sec(\theta)$\), which implies \($dx = \frac{1}{3}\sec(\theta)\tan(\theta)\,d\theta$\). We also need to find a suitable expression for\($\sqrt{9x^2 - 1}$\). From the substitution, we have: \($9x^2 - 1 = 9(\sec^2(\theta)) - 1 = 9\tan^2(\theta)$\).
Substituting these expressions, the integral becomes:
\($\int \frac{1}{x \sqrt{9x^2 - 1}}\,dx = \int \frac{\frac{3}{2}\tan(\theta)}{\frac{1}{3}\sec(\theta)}\,d\theta = \frac{1}{2}\int \sec(\theta)\,d\theta$\)
Using integral tables, the integral of\($\sec(\theta)$\) is \($\ln|\sec(\theta) + \tan(\theta)| + C$\), where \($C$\)is the constant of integration. Therefore, substituting back \($\theta = \sec^{-1}(3x)$\), we have:
\($= \frac{1}{2}\ln|\sec(\sec^{-1}(3x)) + \tan(\sec^{-1}(3x))| + C$$= \frac{1}{2}\ln|3x + \sqrt{9x^2 - 1}| + C$\)
So, the evaluated integral is \($\frac{1}{2}\ln|3x + \sqrt{9x^2 - 1}| + C$\), where\($C$\)represents the constant of integration.
Learn more about integral
https://brainly.com/question/31433890
#SPJ11