Are tools ‘required’ to make accurate and precise measurements?
Answers
Related Questions
Compute the length of the curve r(t)=⟨4cos(5t),4sin(5t),t^3/2) over the interval 0≤t≤2π.
Answers
The length of the curve r(t) over the interval 0 ≤ t ≤ 2π is approximately 285.97 units.
The length of the curve given by the vector-valued function r(t) over the interval [a, b] is given by the formula:
L = ∫[a,b] ||r'(t)|| dt
where r'(t) is the derivative of r(t) with respect to t and ||r'(t)|| is its magnitude.
In this case, we have:
r(t) = ⟨4cos(5t), 4sin(5t), t^(3/2)⟩
r'(t) = ⟨-20sin(5t), 20cos(5t), (3/2)t^(1/2)⟩
||r'(t)|| = √( (-20sin(5t))^2 + (20cos(5t))^2 + ((3/2)t^(1/2))^2 )
||r'(t)|| = √( 400sin^2(5t) + 400cos^2(5t) + (9/4)t )
||r'(t)|| = √( 400 + (9/4)t )
So the length of the curve over the interval [0, 2π] is:
L = ∫[0,2π] √( 400 + (9/4)t ) dt
Making the substitution u = 20t^(1/2)/3, we get:
du/dt = 10t^(-1/2)/3
dt = (3/10)u^(-1/2) du
When t = 0, u = 0, and when t = 2π, u = 20√(π)/3. Substituting these values and simplifying, we get:
L = ∫[0,20√(π)/3] √( 1 + u^2 ) du
Using the substitution x = sinh(u), we get:
dx/dt = cosh(u)
dt = dx/cosh(u)
When u = 0, x = 0, and when u = 20√(π)/3, x = sinh(20√(π)/3). Substituting these values and simplifying, we get:
L = ∫[0,sinh(20√(π)/3)] √( 1 + sinh^2(x) ) dx
L = ∫[0,sinh(20√(π)/3)] cosh(x) dx
Using the formula for the integral of cosh(x), we get:
L = sinh(sinh(20√(π)/3)) - sinh(0)
L ≈ 285.97
Therefore, the length of the curve r(t) over the interval 0 ≤ t ≤ 2π is approximately 285.97 units.
Learn more about length of the curve here
https://brainly.com/question/31376454
#SPJ11
3) If today is Friday, what day of
the week was it 59 days ago?
Answers
Step-by-step explanation:
The answer is friday
I think this is the answer
Answer:
Tuesday
Step-by-step explanation:
If you were to count with your fingers, (which I did) then it would be Tuesday.
Brady has $20,000 in student loans with 3.3% interest that he plans to pay off in 5 years. Find the total cost of repayment.
Answers
The total cost of repayment over 5 years is $23,300.
What is the total cost of repayment?A loan repayment refers to the act of paying back money previously borrowed from a lender.
To get total cost of repayment, we must principal amount, the interest rate and the duration of the loan.
The formula to get total cost of repayment is given by \(Total Cost of Repayment = Principal + Interest\)
Interest = Principal * Interest Rate * Time
Given:
Principal amount is $20,000
Interest rate is 3.3%
Duration is 5 years.
Interest = $20,000 * 0.033 * 5
Interest = $3,300
Total Cost of Repayment = Principal + Interest
= $20,000 + $3,300
= $23,300.
Read more about repayment
brainly.com/question/25696681
#SPJ1
fuwo balls are drawn successively without replacement from a box which contains 4 white balls and 3 red balls. find the probability that both balls are white.
Answers
The probability that both the balls drawn are white is 2/7 when two balls are drawn successively without replacement from a box which contains 4 white balls and 3 red balls.
Two balls are drawn successively without replacement from a box which contains 4 white balls and 3 red balls.
Therefore, Total number of balls in the box = 4+ 3 = 7 balls
Thus, the probability that the first ball drawn is a white is = (Total number of white balls) / ( Total number of balls)
=4/7
The next ball is drawn without replacement thus the number of balls in the box is 6.
And if 1 ball is picked in drawn n first tie, then remaining number of white balls is 3.
Thus, the probability that the second ball drawn is a white is = (Remaining number of total white balls) / ( Remaining number of total balls)
= 3/6 = 1/2
Therefore, the probability that both the balls drawn are white is
= (4/7)*(1/2)
= 2/7
To know more about probability here
https://brainly.com/question/17957560
#SPJ4
can someone please help

Answers
Answer:
for A
the law
V=Bh or V=πr2h
I will use this V=Bh
V= 16·21
V= 336cm³
For E
the law
A= 1/2·(A + B)·H
A= 1/2·(14 + 8)·4
A= 44cm²
V= A·H
V= 44·4
V= 176 cm³
make a search for each one :
B. triangular prism volume calculator
C. pyramid prism volume calculator
D. rectangular prism volume calculator
F. cube volume calculator
Find the critical numbers of the function.
g(y)=(y-1)/(y2-y+1)
Answers
To find the critical numbers of the function \(\(g(y) = \frac{{y-1}}{{y^2-y+1}}\)\), we need to first find the derivative of \(\(g(y)\)\) and then solve for \(\(y\)\) when the derivative is equal to zero. The critical numbers correspond to these values of \(\(y\).\)
Let's find the derivative of \(\(g(y)\)\) using the quotient rule:
\(\[g'(y) = \frac{{(y^2-y+1)(1) - (y-1)(2y-1)}}{{(y^2-y+1)^2}}\]\)
Simplifying the numerator:
\(\[g'(y) = \frac{{y^2-y+1 - (2y^2 - 3y + 1)}}{{(y^2-y+1)^2}} = \frac{{-y^2 + 2y}}{{(y^2-y+1)^2}}\]\)
To find the critical numbers, we set the derivative equal to zero and solve for \(\(y\):\)
\(\[\frac{{-y^2 + 2y}}{{(y^2-y+1)^2}} = 0\]\)
Since the numerator can never be zero, the only way for the fraction to be zero is if the denominator is zero:
\(\[y^2-y+1 = 0\]\)
To solve this quadratic equation, we can use the quadratic formula:
\(\[y = \frac{{-b \pm \sqrt{{b^2-4ac}}}}{{2a}}\]\)
In this case, \(\(a = 1\), \(b = -1\), and \(c = 1\)\). Substituting these values into the quadratic formula, we get:
\(\[y = \frac{{1 \pm \sqrt{{(-1)^2 - 4(1)(1)}}}}{{2(1)}}\]\)
Simplifying:
\(\[y = \frac{{1 \pm \sqrt{{1-4}}}}{{2}} = \frac{{1 \pm \sqrt{{-3}}}}{{2}}\]\)
Since the discriminant is negative, the square root of -3 is imaginary. Therefore, there are no real solutions to the quadratic equation \(\(y^2-y+1=0\).\)
Hence, the function \(\(g(y)\)\) has no critical numbers.
To know more about Function visit-
brainly.com/question/31062578
#SPJ11
Write out the first five terms of the sequence with, [(1−6n+5)n][infinity]n=1[(1−6n+5)n]n=1[infinity], determine whether the sequence converges, and if so find its limit.
Enter the following information for an=(1−6n+5)nan=(1−6n+5)n.
a1=a1=
a2=a2=
a3=a3=
a4=a4=
a5=a5=
limn→[infinity](1−6n+5)n=limn→[infinity](1−6n+5)n=
(Enter DNE if limit Does Not Exist.)
Answers
The required answer is the limit of (-5)^∞ is not well-defined, that the limit Does Not Exist
To find the first five terms of the sequence, we simply substitute n=1,2,3,4,5 into the formula given:
a1=(1-6(1)+5)^1=-1
a2=(1-6(2)+5)^2=0
a3=(1-6(3)+5)^3=27
a4=(1-6(4)+5)^4=256
a5=(1-6(5)+5)^5=3125
To determine whether the sequence converges, we take the limit as n approaches infinity:
limn→[infinity](1−6n+5)n=limn→[infinity](−5n+6)n
We can apply L' Hopital's rule to evaluate this limit:
limn→[infinity](−5n+6)n=limn→[infinity](−5)(−5n+6)n−1=limn→[infinity]−5(−5+6n−2)(n−1)n−2
This limit evaluates to -5, which is a finite number, so the sequence converges.
If such a limit exists, the sequence is called convergent.A sequence that does not converge is said to be divergent. The limit of a sequence is said to be the fundamental notion on which the whole of mathematical analysis ultimately rests
To find the limit of the sequence, we simply take the limit of the formula for an as n approaches infinity:
limn→[infinity](1−6n+5)n=limn→[infinity](−5n+6)n=(-5)^∞
The limit of (-5)^∞ is not well-defined, so we say that the limit Does Not Exist (DNE).
To find the first five terms of the sequence an = (1 - 6n + 5)n, we'll plug in the values n = 1, 2, 3, 4, and 5.
a1 = (1 - 6(1) + 5)(1) = (0)(1) = 0
a2 = (1 - 6(2) + 5)(2) = (-1)(2) = -2
a3 = (1 - 6(3) + 5)(3) = (-2)(3) = -6
a4 = (1 - 6(4) + 5)(4) = (-3)(4) = -12
a5 = (1 - 6(5) + 5)(5) = (-4)(5) = -20
Now, let's examine the limit as n approaches infinity:
A sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called elements, or terms). The number of elements (possibly infinite) is called the length of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an arbitrary index set.
lim(n→∞)(1 - 6n + 5)n
Since the term (1 - 6n + 5) keeps getting smaller (more negative) as n increases, and the term n keeps getting larger, their product will continue to decrease without bound. Therefore, the limit does not exist.
Your answer:
a1 = 0
a2 = -2
a3 = -6
a4 = -12
a5 = -20
lim(n→∞)(1 - 6n + 5)n = DNE
To know more about limit. Click on the link.
https://brainly.com/question/20945705
#SPJ11
please helppppppppppp

Answers
Answer:
2 million 2 3 divided by 3= 20000
Step-by-step explanation:
add and divide
Answer: The answer is after 10 months.
Step-by-step explanation:
So you first start trying to input random numbers up until you get to 10. You multiply 22 by 10 and add an additional 80 making it 300. While when you multiply 30 by 10 you get 300 also.
Each time any customer enters a coffee shop, there
is a probability of that their order will include a
latte.
3
If the order includes a latte, there is a probability of
3 that it will also include a cookie.
4
If the order does not include a latte, there is a
2
probability of that it will include a cookie.
What is the probability that the next customer to
enter the shop will order a cookie?

Answers
The probability that the next customer to enter the shop will order a cookie is given as follows:
31/60.
How to calculate a probability?The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes.
The outcomes in which a cookie is ordered are given as follows:
3/4 of 1/3 -> includes a latte.2/5 of 2/3 -> does not include a latte.Hence the probability is obtained as follows:
3/4 x 1/3 + 2/5 x 2/3 = 1/4 + 4/15 = 15/60 + 16/60 = 31/60.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
I need help asap help me with all questions and please put. The number for the question so I know thank you

Answers
Answer:
1. 6
2. 8
3. 80
4. 11
5. 60
6. 3
7. 30
8. 0.8
9. 5
10. 600
11. 150
12. 110
13. 15
14. 1.1
15. 36
Hope it helps
a pool with dimensions of 10 ft radius and 4 ft height fill with water at a rate of 20 gallons a minutes. about how many hours will it take to fill the pool if 1 cubic foot of water is about 7.5 gallons?
Answers
It will take approximately 7.85 hours to fill the pool.
To determine the time needed to fill the pool, first calculate the volume of the pool, then convert the volume to gallons, and finally, divide by the fill rate.
The pool is a cylinder with a radius of 10 ft and a height of 4 ft. The volume of a cylinder is given by the formula V = πr²h.
V = π(10 ft)²(4 ft) = 400π cubic feet ≈ 1256.64 cubic feet
Next, convert the volume to gallons using the given conversion factor:
1256.64 cubic feet * 7.5 gallons/cubic foot ≈ 9424.8 gallons
Now, divide the total gallons by the fill rate of 20 gallons/minute to find the time in minutes:
9424.8 gallons ÷ 20 gallons/minute ≈ 471.24 minutes
Finally, convert the time to hours:
471.24 minutes ÷ 60 minutes/hour ≈ 7.85 hours
Know more about volume of the pool here:
https://brainly.com/question/8457892
#SPJ11
The population of some bacteria increases by 15% every day. If the original
population was 6000 bacteria, calculate the size of the population after 10 days
Answers
Answer:
To solve this problem, we can use the formula for exponential growth:
N = N0 * (1 + r)^t
Where:
N0 = the initial population size
N = the population size after t time periods
r = the growth rate per time period
t = the number of time periods
In this case, we know that the initial population (N0) is 6000, the growth rate (r) is 15% per day, and we want to find the population size (N) after 10 days (t = 10).
First, we need to convert the growth rate from a percentage to a decimal:
r = 15% / 100% = 0.15
Now we can plug in the values and solve for N:
N = 6000 * (1 + 0.15)^10
N = 6000 * 3.439
N ≈ 20,634
Therefore, the population of bacteria after 10 days would be approximately 20,634.
What is the volume of a rectangular prism with a length of 4. 7 feet, a width of 1. 5 feet, and a height of 1. 6 feet?
O 7. 1 ft
7. 8 ft
O 8. 65 ft
11. 28 ft
Answers
The volume of a rectangular prism with a length of 4.7 feet, a width of 1.5 feet, and a height of 1.6 feet is 11.28 cubic feet.
To find the volume of a rectangular prism, we multiply its length, width, and height. In this case, the length is 4.7 feet, the width is 1.5 feet, and the height is 1.6 feet. By multiplying these values, we get:
Volume = Length x Width x Height
Volume = 4.7 ft x 1.5 ft x 1.6 ft
Volume = 11.28 cubic feet
Therefore, the volume of the given rectangular prism is 11.28 cubic feet.
To learn more about prism click here: brainly.com/question/29077780
#SPJ11
Write the equation of an exponential function that satisfies these characteristics:
1. y intercept of (0,5)
2. range is all y values greater than 0
Answers
The value of the exponential equation is y = 5ˣ + 4
What are the laws of exponents?When you raise a quotient to a power you raise both the numerator and the denominator to the power. When you raise a number to a zero power you'll always get 1. Negative exponents are the reciprocals of the positive exponents.
The different Laws of exponents are:
mᵃ×mᵇ = mᵃ⁺ᵇ
mᵃ / mᵇ = mᵃ⁻ᵇ
( mᵃ )ᵇ = mᵃᵇ
mᵃ / nᵃ = ( m / n )ᵃ
m⁰ = 1
m⁻ᵃ = ( 1 / mᵃ )
Given data ,
Let the exponential equation be represented as A
Now , the value of A is
The y intercept is ( 0 , 5 )
So , when x = 0 , the value of y = 5
Substituting the values in the equation , we get
y = 5ˣ + 4 be equation (1)
when x = 0
y = 5⁰ + 4
y = 1 + 4
y = 5
when x = 2
y = 5² + 4
y = 25 + 4 = 29
Therefore , the range is all y values greater than 0
Hence , the equation is y = 5ˣ + 4
To learn more about exponents click :
https://brainly.com/question/28966438
#SPJ6
Can you find the number bigger than 600 but smaller than 700
Answers
If you have a problem that has multiple variables, you can solve it using a system of equations. Think of a real-world example where you would need to solve using a system of equations. Write two or three sentences describing your example. Include the equations in your description
Answers
Answer:
Suppose you are planning to bake muffins and cupcakes for a bake sale. Muffins require 2 cups of flour and 1 cup of sugar per batch, while cupcakes require 1.5 cups of flour and 2 cups of sugar per batch. If you have 10 cups of flour and 12 cups of sugar available, you can set up a system of equations to determine the number of muffin and cupcake batches you can make.
Let x represent the number of muffin batches and y represent the number of cupcake batches. The system of equations would be:
Equation 1: 2x + 1.5y = 10 (flour constraint)
Equation 2: x + 2y = 12 (sugar constraint)
For each pair of variables, decide whether there is:
• a very weak or no relationship
• a strong relationship that is not a causal relationship
• a causal relationship
_______________________
Explain your reasoning
1. Number of snow plows owned by a city and mitten sales in the city
2. Number of text messages sent per day by a person and number of shirts owned by the person
3. Price of a pizza and number of calories in the pizza
4. Amount of gas used on a trip and number of miles driven on the trip
Answers
Number of snow plows owned by a city and mitten sales in the city - a causal relationship
Number of text messages sent per day by a person and number of shirts owned by the person - a very weak or no relationship
Price of a pizza and number of calories in the pizza - a strong relationship that is not a causal relationship
Amount of gas used on a trip and number of miles driven on the trip - a causal relationship
How do you determine a strong relationship between variables?The strength of a relationship between variables can be determined by calculating the correlation coefficient, which measures the degree of association between two variables.
It's important to keep in mind that correlation does not imply causation, and other factors may be involved in the relationship between variables. Therefore, it's important to carefully interpret the results and consider other relevant information and context.
Learn more about correlation:https://brainly.com/question/30116167
#SPJ1
PLEASE HURY IM TIMED!!!!!!!
pick true or false.
Inequality True False
6.1<6.1
−2≤−2
5.6≥5.6
-4 > 4
Answers
Answer:
Step-by-step explanation:
false true true false
Answer:
false true true and false
Step-by-step explanation:
Label the chart with the correct place value. hundredths tenths thousandths
Answers
Answer:
1020000is a hundredth tenths thousands
what is the list after the second outer loop iteration?[6,9,8,1,7],[],,,
Answers
After the second outer loop iteration, the list is [6,1,7,8,9].
To determine the list after the second outer loop iteration, let's assume we're working with a simple bubble sort algorithm. Here are the steps:
1. First outer loop iteration:
- Compare 6 and 9; no swap.
- Compare 9 and 8; swap to get [6,8,9,1,7].
- Compare 9 and 1; swap to get [6,8,1,9,7].
- Compare 9 and 7; swap to get [6,8,1,7,9].
2. Second outer loop iteration:
- Compare 6 and 8; no swap.
- Compare 8 and 1; swap to get [6,1,8,7,9].
- Compare 8 and 7; swap to get [6,1,7,8,9].
To learn more about loop iteration:
brainly.com/question/30461549
#SPJ11
find the surface area
10in
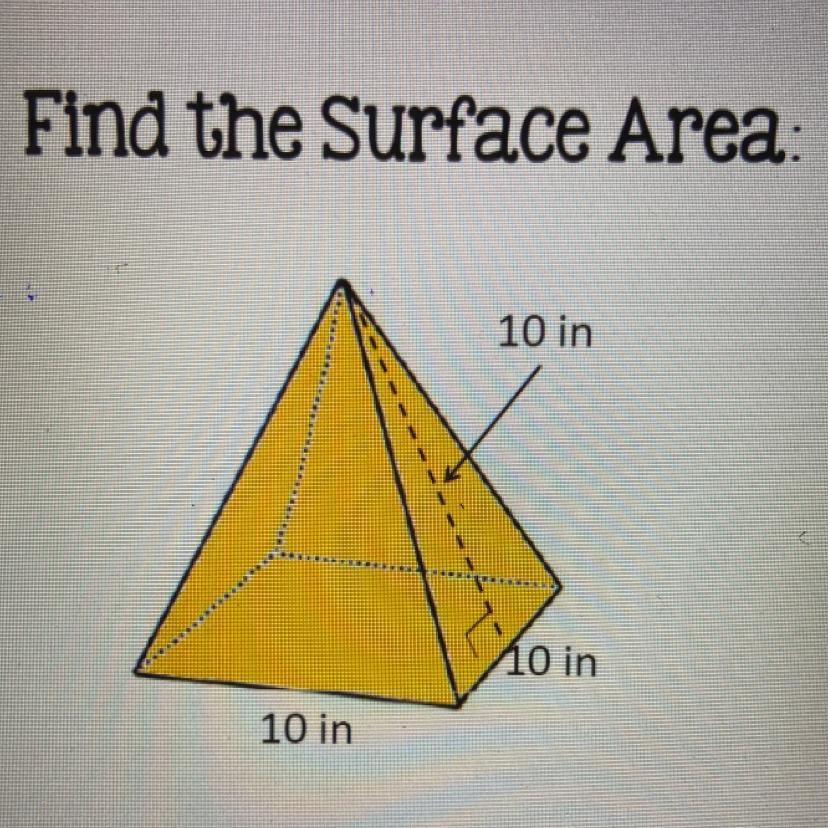
Answers
Answer:
Area of a triangle
\( \frac{bh}{2} \\ 10 \times 10 = 100 \\ 100 \div 2 = 50 \\ the \: triangles \: have \: the \: same \: area \: and \: there \: are \: 4 \: triangles \: so \\ 4(50) = 200 \\ now \: we \: find \: the \: are \: of \: the \: rectangular\: base \: \\ area = bh \\ b = 10 \\ h = 10 \\ 10(10) = 100 \\ no w \: we \: add \: the \: area \: of \: the \: triangles \: and \: the \: square \\ 200 + 100 = 300 \: {in}^{2} \)
What is the measure of angle ABC? pls help fast

Answers
Answer:
(a) 42.5°
Step-by-step explanation:
You want to know the measure of the external angle at two intersecting secants, when they intercept arcs of 25° and 110°.
External angleThe external angle at B is half the difference of the intercepted arcs:
∠ABC = (110° -25°)/2 = 85°/2
∠ABC = 42.5°
__
Additional comment
If the point of intersection (B) moves closer to the circle until it lies on the circle, the secants become chords, and the angle becomes an inscribed angle. Its measure is half the difference between the far arc (AC in this case) and the near arc, which would be zero.
In other words, understanding the relationship in this geometry can help you understand the relationship for inscribed angles.
Give an example of a function between the groups Z6 and Z8 that
is not a homomorphism and why
Answers
The function f(x) = 2x does not preserve the group operation because f(ab) ≠ f(a)f(b).
Therefore, it is not a homomorphism.
The answer to this question is as follows:
Example of a function between the groups Z6 and Z8 that is not a homomorphism and why:
Let Z6 = {0, 1, 2, 3, 4, 5}, and
let Z8 = {0, 1, 2, 3, 4, 5, 6, 7}.
Let f: Z6 → Z8 be the function f(x) = 2x.
We show that f is not a homomorphism.
First of all, to show that f is not a homomorphism, we need to show that it does not preserve the group operation.
That is, we need to find elements a and b in Z6 such that f(ab) ≠ f(a)f(b).
Consider a = 2 and
b = 3
Then ab = 2 × 3
= 0 (mod 6)
Therefore, f(ab) = f(0)
= 0
On the other hand, f(a) = f(2)
= 4, and
f(b) = f(3)
= 6 (mod 8)
Hence, f(a)f(b) = 4 × 6
= 0 (mod 8).
Thus, we have f(ab) = 0
≠ 0
= f(a)f(b), and so f is not a homomorphism.
Basically, a homomorphism is a function between groups that preserves the group operation.
However, in this case, the function f(x) = 2x does not preserve the group operation because f(ab) ≠ f(a)f(b).
Therefore, it is not a homomorphism.
To know more about homomorphism, visit:
https://brainly.com/question/6111672
#SPJ11
Which line has a larger slope?


Answers
Answer:
the one on the right looks best for the slope because the slope is a lot larger than the one on the right the one on the right is smaller but a few inches few times I don't know you might want to check it before I actually answer it for you so I hope you found this kind of helpful thank you bye
madison calculates the mean and standard deviation of chloride values from wells near the seashore. She has performed a(n) ____. A. Interactive query B. Spatial Query C. Attribute Query D. Operation other than a query
Answers
Madison figures out the average and range of chloride readings from wells close to the ocean. Other than a query, she has carried out an operation. The answer id option (d).
What is standard deviation?The standard deviation is a measure of variance from the mean that takes spread, dispersion, and dispersion into account. The standard deviation displays a "typical" divergence from the mean. It is a well-liked measure of variability since it retains the primary units of measurement from the data set. A minor variation occurs when the numbers are close to the mean, while a high variation occurs when they are far from the mean.
The standard deviation describes the degree to which the results deviate from the mean. The average deviation, which depends on all values, is the most often used metric for measuring dispersion. Consequently, the standard deviation's value can be altered even by a slight change in one value.
To know more about standard deviation, visit:
https://brainly.com/question/475676
#SPJ1
If you have the option of choosing a loan that will accumulate 4%/ a interest compounded semi-annually compared to a loan that will accumulate 4% /a interest compounded monthly, which one would you choose
Answers
Answer:
4%/ a interest compounded semi-annually
Step-by-step explanation:
The option that gives the lower interest rate payment would be more appropriate. to determine this calculate the effective interest rate
Effective annual rate = (1 + APR / m ) ^m - 1
M = number of compounding
(1 + 0.04/2)^2 - 1 = 4.04%
(1 + 0.04/12)^12 - 1 = 4.07%
the choice should be 4%/ a interest compounded semi-annually
what is m
help ASAP pleasee!!

Answers
The sum of angles of a triangle equals 180°.
Therefore:
|∠EAB| + |∠ABE| + |∠BEA| = 180°
Susbtitute
|∠EAB| = 14°
|∠ABE| = 45°
|∠BEA| = x°
14° + 45° + x° = 180°
59° + x° = 180° |subtract 59° from both sides
x° = 121°∠BEA and ∠CED are vertical angles. Vertical angles are congruent, meaning that they have the same angle measure.
Therefore
|∠CED| = 121°In ΔCDE:
|∠CED| + |∠DCE| + |∠EDC| = 180°
Substitute:
|∠CED| =121°
|∠DCE| = 27°
|∠EDC| = y°
121° + 27° + y° = 180°
148° + y° = 180° |subtract 148° from both sides
y° = 32°|∠EDC| = 32°consider what you know about the sampling distribution of the sample proportion. this sampling distribution
Answers
Consider what you know about the sampling distribution of the sample proportion. this sampling distribution will have a centre equal to the population proportion, or p.
For determining the correct option, we will check one by one all the given options:
From the given statements, we can conclude that.
As the sample size of the data increases, the corresponding value of n also starts increasing.
The value on the denominator of the standard deviation equation is n.
Therefore, the standard deviation will decrease as the value of n increases.
A tiny variance is one with a low standard deviation.
As a result, the variance will be minor as the sample size increases.
For more questions on sampling distribution
brainly.com/question/29368683
#SPJ4
Actual questions should be:
Consider what you know about the sampling distribution of the sample proportion. This sampling distribution
(1) has a shape that is skewed to the right, regardless of sample size.
(2) is a collection of the parameters of all possible samples of a particular size taken from a particular population.
(3) Will become more variable as the sample size increases.
(4) will have a center equal to the population proportion, or p.
(5) will be Normal in shape only if the sample size is at least 100 .
how are these 2 numbers different (image above)

Answers
Answer:
one of them has a dividend the other doesnt
Step-by-step explanation:
what is 3/12 converted into over 100
Answers
The value of 3/12 of 100 is 25 .
In the question ,
a fraction 3/12 is given ,
we have to find the value of 3/12 of 100 .
to find the value , we first convert both the numbers into fraction
So 100 in fraction form can be written as 100/1
So the value 3/12 of 100 means
= \(\frac{3}{12} *\frac{100}{1}\)
multiplying the numerator with numerator
and multiplying denominator with denominator .
we get = 300/12
on further simplification ,
we have ,
= 75/3
= 25
So , 3/12 of 100 = 25
Therefore , The value of 3/12 of 100 is 25 .
The given question is incomplete , the complete question is
What is the value of 3/12 of 100 ?
Learn more about Fraction here
https://brainly.com/question/1937550
#SPJ1