As storm clouds gathered, the temperature fell 4 degrees in 3/4 of an hour. At what rate was the temperature falling?
Answers
Answer:
5 1/3
Step-by-step explanation:
Answer:
5 1/3
Step-by-step explanation:
Related Questions
FInd the slope y = -2
Answers
Answer:
The slope is ZERO. It has no slope
Step-by-step explanation:
If you have a bit of honesty and sincerity, kindly avoid spamming just for points!
A production process consists of consumption of the following material in Kgs:
49, 50, 38, 60, 75 of materials A, B, C, D. E respectively. How many angle difference between C & D in the pie chart?
a. 25.12% b. 29.12% C.38.15
Need solution with some explanation
Answers
Answer:
29.12%
Step-by-step explanation:
Given that :
A = 49
B = 50
C = 38
D = 60
E = 75
Total = (49 + 50 + 38 + 60 + 75) = 272
Pie chart % for each :
A = (49 / 272) * 360 = 64.85
B = (50 / 272) * 360 = 66.18
C = (38 / 272) * 360 = 50.29
D = (60 / 272) * 360 = 79.41
E = (75 / 272) * 360 = 99.26
Difference between C and D
(79.41 - 50.29) = 29.12%
Express as a trinomial.
(x-1)(2x-8)
(x−1)(2x−8)
Answers
Answer:
this is a binomial, but its 2x^2-10x+8
Step-by-step explanation:
you use the distributive property
Pls someone help me!!

Answers
88% as a fraction 
Answers
To express 88% as a fraction, we can write it as 88/100. However, we can simplify this fraction by dividing both the numerator and denominator by their greatest common divisor, which is 4. So, 88/100 simplifies to 22/25. Therefore, 88% can be expressed as the fraction 22/25.
~~~Harsha~~~
please help me!!!!!!!!!!!!

Answers
Answer:
Hello,
Answer A
Step-by-step explanation:
Not C since for x=-1,y=(-1-5)²+78= 36+78 ≠ 0
Not D since for x=-1, y= (-1)²+2=1+2=3 ≠ 0
remains A and B
Not B since for x=0, y=0²-1=-1 ≠ -2
Verifying A:
F(-1)=3*(-1)²+(-1)-2=3-3=0 ok
F(0)=3*0²+0-2=-2 ok
F(5)=3*5²+5-2=75+3=78 ok
F(10)=3*10²+10-2=300+8=308 ok
Answer A
(5 pts) 1. Which of the following lines is orthogonal to the plane $2 x+4 y-2 z=10$ ?
A. $r(t)=\langle 3-t, 5,6+t\rangle, t \in(-\infty, \infty)$
B. $r(t)=\langle 1+t,-1+t, 4+t\rangle, t \in(-\infty, \infty)$
C. $\mathbf{r}(t)=\langle 2+2 t, 5+t, 7\rangle, t \in(-\infty, \infty)$
D. $r(t)=\langle-12-t,-5+t, 6+t\rangle, t \in(-\infty, \infty)$
E. none of the above
Answers
The correct answer is A.To determine which line is orthogonal to the plane, we need to find the direction vector of the line and check if it is orthogonal to the normal vector of the plane.
The normal vector of the plane 2x + 4y - 2z = 10 is [2, 4, -2].
Calculating the dot product of this normal vector with the direction vectors of the given lines, we find:
A. [2, 4, -2] ⋅ [-1, 0, 1] = 0 (orthogonal)
B. [2, 4, -2] ⋅ [1, 1, 1] = 4 (not orthogonal)
C. [2, 4, -2] ⋅ [2, 1, 0] = 4 (not orthogonal)
D. [2, 4, -2] ⋅ [-1, 1, 1] = 0 (orthogonal)
Based on the dot products, options A and D have direction vectors that are orthogonal to the plane. Therefore, the lines described by options A and D are orto to the plane. The correct answer is A.
To learn more about vector click here:brainly.com/question/30958460
#SPJ11
A clock is constructed using a regular polygon with 60 sides. The polygon rotates each minute, making one full revolution each hour. How much has the polygon rotated after 7 minutes?
14°
21°
35°
42°
Answers
Answer:
42
Step-by-step explanation:
Answer: D. 42°
Step-by-step explanation: RIGHT ON EDGE 2023
which shows how the distributive property can be used to evaluate 7 times 8 and four-fifths? 56 startfraction 28 over 5 endfraction
Answers
56 * (28/5) shows how the distributive property can be used to evaluate 7 times 8 and four-fifths.
7 times 8 = 56
4/5 = 28/5
Using the distributive property:
7 * 8 * (4/5) = (7 * 8) * (4/5) = 56 * (4/5) = 56 * (28/5) = 56 startfraction 28 over 5 endfraction
The distributive property states that for any numbers a, b, and c, a * (b + c) = a * b + a * c. To evaluate 7 times 8 and four-fifths, we can use the distributive property to separate the two factors. First, we calculate 7 times 8, which is equal to 56. Then, we calculate four-fifths, which is equal to 28/5. We then use the distributive property to multiply the two factors together, which is (7 * 8) * (4/5). This simplifies to 56 * (4/5) which is equal to 56 startfraction 28 over 5 endfraction.
Learn more about distributive property here
https://brainly.com/question/5637942
#SPJ4
. You deposit $200 each month into an account earning 3% interest compounded monthly for 30 years. How much total interest will you earn in 30 years?
Answers
The total interest you will earn in 30 years is approximately $241.61.
To calculate the total interest earned in 30 years, we need to use the formula for compound interest:
A = P(1 + r/n)^(nt) - P
Where:
A = the future value of the investment
P = the principal amount (initial deposit)
r = the annual interest rate (in decimal form)
n = the number of times the interest is compounded per year
t = the number of years
In this case, the principal amount is $200, the annual interest rate is 3% (or 0.03 as a decimal), the interest is compounded monthly (so n = 12), and the time period is 30 years (so t = 30).
Plugging in these values into the formula:
A = 200(1 + 0.03/12)^(12*30) - 200
Now we can simplify and calculate:
A = 200(1.0025)^(360) - 200
A = 200(2.208040033) - 200
A ≈ 441.6080066 - 200
A ≈ 241.6080066
For more such questions on approximately
https://brainly.com/question/29985480
#SPJ8
What is the value of x in the equation. 1/2x - 3/4 = 3/8 - 5/8x?

Answers
Answer:
x=1
Step-by-step explanation:
simplify and create a chart of denominators until you find the common one.
Answer:
Step-by-step explanation:
1/2x - 3/4 = 3/8 - 5/8x
+ 5/8x + 5/8x
9/8x - 3/4 = 3/8
+ 3/4 + 3/4
9/8x = 9/8
divide both sides by 9/8
x = 1
very fast
Show, by induction, that \( T(n)=10 n^{2}-3 n \quad \) if \( n=1 \)
Answers
Given that \(\(T(n)\) = \(10n^2-3n\)\) if (\(\(n=1\)\)), you have to prove it by induction. So, we have proved it by induction that \($$\(T(n)=10n^2-3n\)$$\) if ( n= 1). The given statement is true for all positive integers n
Let's do it below: The base case (n=1) is given as follows: \(T(1)\) =\(10\cdot 1^2-3\cdot 1\\&\)=\(7\end{aligned}$$\). This implies that \(\(T(1)\)\) holds true for the base case.
Now, let's assume that \(\(T(k)=10k^2-3k\)\) holds true for some arbitrary \(\(k\geq 1\).\)
Thus, for n=k+1, T(k+1) = \(10(k+1)^2-3(k+1)\\&\) = \(10(k^2+2k+1)-3k-3\\&\)=\(10k^2+20k+7k+7\\&\) = \(10k^2-3k+20k+7k+7\\&\) = \(T(k)+23k+7\\&\) = \((10k^2-3k)+23k+7\\&\) = \(10(k+1)^2-3(k+1)\).
Therefore, we have proved that the statement holds true for n=k+1 as well. Hence, we have proved it by induction that \($$\(T(n)=10n^2-3n\)$$\) if (n=1). Therefore, the given statement is true for all positive integers n.
For more questions on: integers
https://brainly.com/question/17695139
#SPJ8
An automobile uses 17 gal of fuel to go 590 mi. how many gallons are required to travel 840 mi? (round your answer to one decimal place.)
Answers
Answer:
the car would use 49 gallons because you get a decimal of 49.49 so you would put got decimal to the nearest 1's place and that would be 49
Choose the system of equations which matches the following graph.
A. 3x-6y=12
9x-18y=36
B. 3x+6y=12
9x+18y=36
Answers
The system of equations that matches the given graph is:
A. 3x - 6y = 12
9x - 18y = 36
To determine which system of equations matches a given graph, we need to analyze the slope and intercepts of the lines in the graph.
Looking at the options provided:
A. 3x - 6y = 12
9x - 18y = 36
B. 3x + 6y = 12
9x + 18y = 36
Let's analyze the equations in each option:
For option A:
The first equation, 3x - 6y = 12, can be rearranged to slope-intercept form: y = (1/2)x - 2.
The second equation, 9x - 18y = 36, can be simplified to 3x - 6y = 12, which is the same as the first equation.
In option A, both equations represent the same line, as they are equivalent. Therefore, option A does not match the given graph.
For option B:
The first equation, 3x + 6y = 12, can be rearranged to slope-intercept form: y = (-1/2)x + 2.
The second equation, 9x + 18y = 36, can be simplified to 3x + 6y = 12, which is the same as the first equation.
In option B, both equations also represent the same line, as they are equivalent. Therefore, option B does not match the given graph.
for such more question on system of equations
https://brainly.com/question/4262258
#SPJ8
how many ways are there to select 9 players for the starting lineup and a batting order for the 9 starters? g
Answers
There are 362,880 ways to select 9 players for the starting lineup and a batting order for the 9 starters based on the concept of combinations.
To calculate the number of ways to select 9 players for the starting lineup, we need to consider the combination formula. We have to choose 9 players from a pool of players, and order does not matter. The combination formula is given by:
\(C(n, r) =\frac{n!}{(r!(n - r)!}\)
Where n is the total number of players and r is the number of players we need to select. In this case, n = total number of players available and r = 9.
Assuming there are 15 players available, we can calculate the number of ways to select 9 players:
\(C(15, 9) = \frac{15!}{9!(15 - 9)!} = \frac{15!}{9!6!}\)
To determine the batting order, we need to consider the permutations of the 9 selected players. The permutation formula is given by:
P(n) = n!
Where n is the number of players in the batting order. In this case, n = 9.
P(9) = 9!
Now, to calculate the total number of ways to select 9 players for the starting lineup and a batting order, we multiply the combinations and permutations:
Total ways = C(15, 9) * P(9)
= (15! / (9!6!)) * 9!
After simplification, we get:
Total ways = 362,880
There are 362,880 ways to select 9 players for the starting lineup and a batting order for the 9 starters. This calculation takes into account the combination of selecting 9 players from a pool of 15 and the permutation of arranging the 9 selected players in the batting order.
To know more about Combination, visit
https://brainly.com/question/28065038
#SPJ11
there are four nickels and eight dimes in your pocket. you randomly pick a coin out of your pocket and then return it to your pocket. then you randomly pick another coin. find the probability that both times the coin is a nickel.
Answers
The probability of randomly picking a nickel twice in a row from four nickels and eight dimes is 1/9.
Given that there are four nickels and eight dimes in your pocket, the total number of coins is twelve. If you randomly pick a coin and then return it to your pocket, there are still twelve coins in your pocket, and the probability of picking a nickel remains the same. Therefore, the probability of picking a nickel on the first draw is 4/12, which simplifies to 1/3.
Now, you pick another coin from the pocket, and again there are twelve coins. Since the first coin was returned to the pocket, the probability of picking a nickel on the second draw is also 4/12 or 1/3.
To calculate the probability of both events occurring together, we multiply the probability of the first event by the probability of the second event.
Thus, the probability of picking a nickel on the first draw AND picking a nickel on the second draw is (1/3) x (1/3) = 1/9.
To know more about probability here
https://brainly.com/question/11234923
#SPJ4
Show that f is continuous on (−[infinity], [infinity]). f(x) = 1 − x2 if x ≤ 1 ln(x) if x > 1
On the interval
(−[infinity], 1),
f is function; therefore f is continuous on
(−[infinity], 1).
On the interval
(1, [infinity]),
f is function; therefore f is continuous on
(1, [infinity]).
Answers
The function \($$f(x)= \begin{cases}1-x^2 & x \leqslant 1 \\ \ln (x) & x \geqslant 1\end{cases}$$\) is continuous on (-∞, ∞).
As per the given data the function f(x) is given by:
\($$f(x)= \begin{cases}1-x^2 & x \leqslant 1 \\ \ln (x) & x \geqslant 1\end{cases}$$\)
Here we have to determine that the function f(x) is continuous on (-∞, ∞)
If we show that f(x) is continuous at x = 1 then f(x) is continuous on (-∞, ∞)
What are continuous function?
A continuous function in mathematics is one where changes in the parameter cause constant changes in the function's value (i.e., a change without a leap). This shows that there are no abrupt changes in value or discontinuities.
To show f(x) is continuous at x = 1
\(\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{+}}\) f(x)
\(\rightarrow \lim _{x \rightarrow 1^{-}} f(x) & =\lim _{x \rightarrow 1^{-}}\left(1-x^2\right) \\\)
= 1 - 1
= 0
\(\lim _{x \rightarrow 1^{+}} f(x) & =\lim _{x \rightarrow 1^{+}} \ln (x) \\\)
= ln 1
= 0
Therefore \(\lim _{x \rightarrow 1^{+}} f(x) & =\lim _{x \rightarrow 1^{-}} f(x)-0\).
Hence f(x) is continuous on (-∞, ∞)
For more questions on Limits
https://brainly.com/question/20067425
#SPJ4
Pleaseee help! I WILL MARK BRAINLIEST.
The approximate weights of two animals are 4.23 x 103 lbs. and 8.7 x 103 lbs. Find the total weight of the two animals. Write the final answer in scientific notation with the correct number of significant digits. 1.29 x 104 lbs. 1.3 x 104 lbs. 5.1 x 103 lbs. 12 x 103 lbs.
Answers
The total weight of the two animals is 1.3 x 10^4 lbs.
How to determine the total weight of the two animals?The given parameters are
Animal 1 = 4.23 x 103 lbs.
Animal 2 = 8.7 x 103 lbs.
Rewrite the parameters properly
Animal 1 = 4.23 x 10^3 lbs.
Animal 2 = 8.7 x 10^3 lbs.
The total weight of the two animals is calculated as
Total weight = Animal 1 + Animal 2
This gives
Total weight = 4.23 x 10^3 lbs + 8.7 x 10^3 lbs.
Factor out 10^3 lbs
Total weight = (4.23 + 8.7) x 10^3 lbs.
Evaluate the sum
Total weight = 12.93 x 10^3 lbs.
Rewrite as
Total weight = 1.293 x 10^4 lbs.
Approximate
Total weight = 1.3 x 10^4 lbs.
Hence, the total weight of the two animals is 1.3 x 10^4 lbs.
Read more about scientific notation at:
https://brainly.com/question/5756316
#SPJ1
Solve the system of equations by substitution.
y = 4x -1
2x + 2y = 3
Answers
Step-by-step explanation:
y = 4x - 1
2x + 2y = 3
2x + 2(4x - 1) = 3
2x + 8x - 2 = 3
10x = 3 + 2
x = 5/10
x = 1/2
y = 4x - 1
y = 4(1/2) - 1
y = 2 - 1
y = 1
(x,y) = (1/2 , 1)
A study is done to determine the attitudes of male university students towards careers. The researcher interviews 100 of the male students enrolled in a first-year course at the university. What is the sample in this situation?
all university students
male university students
the male students taking this course
the 100 male students interviewed
Answers
Answer:
I need the answer
Step-by-step explanation:
Answer:
Step-by-step explanation:
The sample is the part of the population that somebody wants to study. therefore, the sample is the 100 male students interviewed
A point is a physical measurement approximately equal to 1/16th of an inch. Group of answer choices False True
Answers
4. In how many ways can 5 men and 7 women be seated in a row so that no two men are next to each other? You must justify your answer.
Answers
Answer:
3628800 ways if the women are always required to stand together.
To solve this problem, we can consider the number of ways to arrange the women and men separately, and then multiply the results together.
First, let's consider the arrangement of the women. Since no two men can be seated next to each other, the women must be seated in between the men. We can think of the 5 men as creating 6 "gaps" where the women can be seated (one gap before the first man, one between each pair of men, and one after the last man).
Out of these 6 gaps, we need to choose 7 gaps for the 7 women to sit in. This can be done in "6 choose 7" ways, which is equal to the binomial coefficient C(6, 7) = 6!/[(7!(6-7)!)] = 6.
Next, let's consider the arrangement of the 5 men. Once the women are seated in the chosen gaps, the men can be placed in the remaining gaps. Since there are 5 men, this can be done in "5 factorial" (5!) ways.
Therefore, the total number of ways to seat the 5 men and 7 women is 6 * 5! = 6 * 120 = 720.
There are 720 ways to seat the 5 men and 7 women in a row such that no two men are next to each other.
To know more about arrangement visit
https://brainly.com/question/1427391
#SPJ11
please this asap thank you We wish to estimate what proportion of adult residents in a certain county are parents.Out of 200 adult residents sampled,160 had kids.Based on this,construct a 93% confidence interval for the proportion p of adult residents who are parents in this county. Express your answer in tri-inequality form. Give your answers as decimals,to three places. Express the same answer using the point estimate and margin of error. Give your answers as decimals,to three places.
Answers
We can be 93% confident that the true proportion of adult residents who are parents in this county lies between 0.74 and 0.86.
To find the z-score corresponding to a 93% confidence level, we need to determine the critical value. We can use a standard normal distribution table or a calculator to find this value. For a two-tailed test, the critical value corresponds to (1 - (1 - confidence level) / 2).
Using the formula:
Critical value = (1 - (1 - 0.93) / 2) = (1 - 0.07 / 2) = 0.965
Now we have the critical value, z = 0.965. Substituting the values into the formula, we can calculate the margin of error:
Margin of error = z * sqrt((p * (1 - p)) / n)
= 0.965 * √((0.8 * (1 - 0.8)) / 200)
≈ 0.060
Finally, we can construct the confidence interval using the sample proportion and the margin of error:
Confidence interval = p ± margin of error
= 0.8 ± 0.060
Expressing this in the tri-inequality form, we have:
0.8 - 0.060 < p < 0.8 + 0.060
Simplifying the inequality, we get:
0.74 < p < 0.86
This means that if we were to take many samples and construct confidence intervals for each sample, approximately 93% of those intervals would contain the true population proportion.
To know more about confidence interval here
https://brainly.com/question/24131141
#SPJ4
answer and you'll get brainliest!

Answers
Answer:
part b
Step-by-step explanation:
denominater remains same,numerater will add up
1+1+1+1+1+1+1=7
hence
it will become 7/8
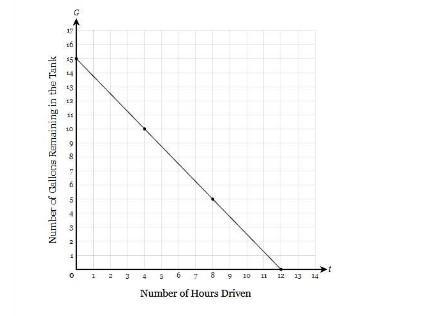
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
HELP HELP HELP!!!!!is this correct?if not which one is correc

Answers
Answer:
Step-by-step explanation:
it has 2 solutions, 0 and 11
1 + 3/4 =? trying to figure this out!
Answers
Answer:
1.75 as a decimal or 1 3/4 as a mixed number
Tom rolls 2 fair dice and adds the results from each.
Work out the probability of getting a total more than 4.
Answers
Answer:
1/6
Step-by-step explanation:
hii i’ll give brainliest please help thanks :)

Answers
Answer:
85
Step-by-step explanation:
Answer:
its 85
Step-by-step explanation:
The box plots below show the distributions of the
numbers of visitors each day to two attractions.
a) Work out the interquartile range of the numbers of
visitors to
i) the museum.
ii) the farm.
b) Copy and complete the sentences below.
Museum
H
Farm
H
0 100 200 300 400 500 600 700 800
Number of visitors
The interquartile range for the museum is greater / less than the interquartile range for the farm.
This suggests that the numbers of visitors to the museum are more/less consistent.

Answers
The interquartile range for the museum is 280
The interquartile range for the farm is 200
The interquartile range for the museum is greater than the interquartile range for the farm.
This suggests that the numbers of visitors to the museum are less consistent.
How to find the interquartile rangeThe interquartile range is solved using the formula
= top quartile - bottom quartile
Where
the bottom quartile is at the box's edge, the top side.
the top quartile is towards the box's edge the downside.
the museum
The interquartile range is
= top quartile - bottom quartile
= 500 - 220
= 280
the farm
The interquartile range is
= top quartile - bottom quartile
= 460 - 260
= 200
Learn more about box plot at:
https://brainly.com/question/29862893
#SPJ1