ASAP please help
This graph shows how many cookies Julia makes over 9 days.
a) How many total cookies will Julia have on
day 7?
b) Estimate the output when the input is 2.

Answers
b. approximately 250
Answer for (B) 250
Hope this helps!
Related Questions
T/F,the assumption for normality usually holds in any distribution so long as precise calculations of z statistics are made.
Answers
The given statement "The assumption for normality usually holds in any distribution so long as precise calculations of z statistics are made" is False because these tests do not rely on the normality assumption and can provide more accurate results when working with non-normal distributions.
Normality refers to a distribution that follows a normal or Gaussian distribution, characterized by a bell-shaped curve that is symmetric around the mean. The assumption of normality is an important aspect of many statistical tests, such as the t-test or ANOVA, which rely on the data being normally distributed to draw accurate conclusions.
Precise calculations of z statistics, which standardize individual data points based on the mean and standard deviation, do not guarantee that the assumption of normality holds. While these calculations can help compare and analyze data from different distributions, they do not transform a non-normal distribution into a normal one.
If the assumption of normality does not hold, alternative non-parametric tests, such as the Mann-Whitney U test or the Kruskal-Wallis test, should be used to analyze the data.
Know more about Normality here:
https://brainly.com/question/14005451
#SPJ11
Solve the following systems of equations using Gaussian Elimination. 2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Find the inner product of two vectors A = (2, -3,0) and B = = (-1,0,5)
Answers
The inner product of two vectors A = (2, -3,0) and B = (-1,0,5) is -2 / √(13×26).
Solving the given system of equations using Gaussian elimination:
2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Matrix form of the system is
[A] = [B] 2 3 1 | 2 0 5 | 20 -1 2 3 | 13
Divide row 1 by 2 and replace row 1 by the new row 1: 1 3/2 1/2 | 1
Divide row 2 by 5 and replace row 2 by the new row 2: 0 1 1 | 4
Divide row 3 by -1 and replace row 3 by the new row 3: 0 0 1 | 5
Back substitution, replace z = 5 into second equation to solve for y, y + 5(5) = 20 y = -5
Back substitution, replace z = 5 and y = -5 into the first equation to solve for x, 2x + 3(-5) + 5 = 2 2x - 15 + 5 = 2 2x = 12 x = 6
The solution is (x,y,z) = (6,-5,5)
Therefore, the solution to the given system of equations using Gaussian elimination is (x,y,z) = (6,-5,5).
The given two vectors are A = (2, -3,0) and B = = (-1,0,5). The inner product of two vectors A and B is given by
A·B = |A||B|cosθ
Given,A = (2, -3,0) and B = (-1,0,5)
Magnitude of A is |A| = √(2²+(-3)²+0²) = √13
Magnitude of B is |B| = √((-1)²+0²+5²) = √26
Dot product of A and B is A·B = 2(-1) + (-3)(0) + 0(5) = -2
Cosine of the angle between A and B is
cosθ = A·B / (|A||B|)
cosθ = -2 / (√13×√26)
cosθ = -2 / √(13×26)
Learn more about equation at
https://brainly.com/question/12998758
#SPJ11
PLEASE HURRY I HAVE TO FINISH THIS TODAY
Which of the following apply to a isosceles trapezoid?
I it will have a midsegment.
II The base angles are congruent.
III The same side interior angles are complementary.
Answers
Answer:
II
Step-by-step explanation:
The base angles of an isosceles trapezoid are congruent.
Also, if you could label this brainliest that would be a great help!
Thanks xx
-Dante
The addition rule is used to calculate Multiple choice question. the independence of two events. the conditional probability of two events. the union of two events. the intersection of two events.
Answers
The addition rule is used to calculate the union of two events.
Explanation:
In probability theory, the addition rule is a fundamental principle that allows us to calculate the probability of the union of two events. The union of two events refers to the event that either one event occurs or the other event occurs, or both events occur simultaneously.
The addition rule states that the probability of the union of two events A and B is equal to the sum of their individual probabilities minus the probability of their intersection:
The addition rule is used to calculate the union of two events. It is given by the formula:
\(\[ P(A \cup B) = P(A) + P(B) - P(A \cap B) \]\)
where \(\( P(A) \)\) represents the probability of event A, \(\( P(B) \)\) represents the probability of event B, and \(\( P(A \cap B) \)\) represents the probability of the intersection of events A and B.
You can use this rule to calculate the probability of the union of two events in various probability problems.
In other words, to calculate the probability of either event A or event B occurring (or both), we add the probabilities of the individual events and then subtract the probability of their intersection to avoid double-counting.
To know more about Calculate visit-
brainly.com/question/31718487
#SPJ11
Please help with the last equation on the bottom.

Answers
Answer:
0.5
Step-by-step explanation:
the guy took 15 pieses and there is 4 left

Answers
The number of pieces in the bowl before she added the 20 is 8 pieces of candy
Here, we want to get the number of pieces in the bowl before the addition of the 20 pieces
Let the number of pieces before the addition be n
she added 20 pieces to what is there initially, this brings the total to;
\(n\text{ + 20}\)Now, two days after the addition, half of the above is gone
Half of the above is;
\(\frac{n+20}{2}\)Now, the difference between the number of pieces in the bowl after the addition of the 20 and the half gone is 14; we have the equation as thus;
\(\begin{gathered} n\text{ + 20 - (}\frac{n+20}{2})\text{ = 14} \\ \\ 2(n+20)-(n+20)\text{ = 28} \\ n\text{ +20 = 28} \\ n\text{ = 28-20} \\ n\text{ = 8} \end{gathered}\)Simple Math!! 2581 ÷ 21
Answers
Answer:
\(122\frac{19}{21}\) or \(122.904\)
Step-by-step explanation:

2581 ÷ 21 = 122.9
Use a calculator
what are the minimum and maximum temperatures in the house ?
Answers
Answer:
I mean, I think it varies by house and by location but a general range would be:
Min: 64 *F
Max: 74 *F
a jeweler had a fixed amount of gold to make bracelets and necklaces. The amount of gold in each bracelet is 5 grams and the amount of gold in each necklace is 16 grams. a jeweler used 130 grams
Answers
The number of bracelets and the number of necklaces will be 10 and 5, respectively.
What is a linear equation?A connection between a number of variables results in a linear model when a graph is displayed. The variable will have a degree of one.
A gem dealer had a proper measure of gold to make wristbands and pieces of jewelry. The amount of gold in every armband is 5 grams and the amount of gold in every accessory is 16 grams. A goldsmith utilized 130 grams.
Let 'x' be the number of Bracelets and 'y' be the number of Necklaces. Then the equation is given as,
5x + 16y = 130
The term 16y in the equation should be a multiple of 5 to get the whole value.
If the value of y is 5. Then the number of bracelets is given as,
5x + 16(5) = 130
5x + 80 = 130
5x = 50
x = 10
The number of bracelets and the number of necklaces will be 10 and 5, respectively.
More about the linear equation link is given below.
https://brainly.com/question/11897796
#SPJ2
Through a diagonalization argument, we can show that |N] + [[0, 1] |. Then, in order to prove |R| # |N|, we just need to show that | [0, 1] | = |R) Select one: True O False.
Answers
False. a diagonalization argument, we can show that |N] + [[0, 1] |. Then, in order to prove |R| # |N|, we just need to show that | [0, 1] | = |R) S
The statement "| [0, 1] | = |R)" is not true.
The set [0, 1] represents the interval of real numbers between 0 and 1, while R represents the set of all real numbers. The cardinality of the set of real numbers (R) is equal to the cardinality of the set of points on a line, which is uncountably infinite (i.e., greater than aleph-null, the cardinality of the set of natural numbers). On the other hand, the cardinality of [0, 1] is the same as that of any interval of real numbers, which is also uncountable.
Therefore, neither set has the same cardinality as the other, and we cannot prove that |R| # |N| just by showing that | [0, 1] | = |R). Other methods must be used to demonstrate that the cardinality of the real numbers is greater than the cardinality of the natural numbers.
Learn more about diagonalization argument here
https://brainly.com/question/29974985
#SPJ11
how do i find whether it is sss sas or aas or hl?

Answers
Answer:
easy it 53847263
Step-by-step explanation:
it is
Answer:
A: SSS | B: HL | C: SAS
Step-by-step explanation:
Firstly, SSS is where you know that each side of a triangle is congruent to the other triangle.
Secondly, SAS is where you know two sides and an angle are congruent. This angle will be between two sides that are congruent. This can be put clockwise or counterclockwise, but the sides and angle must be consecutive.
Thirdly, AAS is where you know two angles and one side are congruent.
Lastly, HL (Theorem) is where you know that the hypotenuse and a leg of a right triangle are congruent.
A: TU≅WX, ST≅XV, and SU≅VW
B: Two right triangles; HA and OK are the hypotenuses, and HA≅OK, RH≅RK
C: ZW≅YX, ∠W≅∠X, and WX≅WX
Use the data table below to create the given scatter plot, then fill in the guided sentence below. I just need the sentence.

Answers
Using visual interpretation of the plot trend, the scatter plot shows positive correlation.
A positive correlation is depicted by a positive slope or trend line on a scatter plot. The trend of the scatter plot slopes upward which establishes a positive association.
If the slope is otherwise negative, such that the trend line slopes downward, then we have a negative association or relationship.
Therefore, the scatter plot shows positive relationship.
Learn more on scatter plot:https://brainly.com/question/6592115
#SPJ1
Please help 6th grade math please please help
if you dont know the answer please do not answer this question

Answers
Answer:
Least Value: 16
Median: 26
Upper Quartile: 30
Lower Quartile: 20
Greatest Value: 34
Interquartile Range: 10
Range: 18
Use the drop-down menus to complete the solution to the equation cosine (startfraction pi over 2 endfraction minus x) = startfraction startroot 3 endroot over 2 endfraction for all possible values of x on the interval [0, 2pi].
Answers
Use the drop-down menus to complete the solution to the equation cosine (start fraction pi over 2 end fraction minus x) = start fraction start root 3 end root over 2 end fraction for all possible values of x on the interval [0, 2pi].
Using trigonometric identities, the solution to the equation \(cos(\frac{\pi }{2}-x) = \frac{\sqrt{3} }{2}\) for all possible values of x on the interval [0, 2π].
What are trigonometric identities?
Trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined.
\(cos(\frac{\pi }{2}-x) = \frac{\sqrt{3} }{2} \\\\cos(x)cos\frac{\pi }{2}+sin(x)sin \frac{\pi }{2} = \frac{\sqrt{3} }{2}\\\\cos(x)(0)+sin(x)(1) = \frac{\sqrt{3} }{2}\\\\sin(x) = \frac{\sqrt{3} }{2}\\\\x = \frac{\pi }{3}, \frac{2\pi }{3}\)
To learn more about trigonometric identities click here https://brainly.com/question/7331447
#SPJ4
how many different 9-digit pins are there where exactly three of the digits are the same and none of the remaining digits may be repeated?
Answers
This can be calculated by taking 10 (the number of digits available) to the power of 6 (the number of digits that must be different) and multiplying that by 10 (the number of digits available to be repeating number). 10^6 * 10 = 3,628,800.
The number of different 9-digit pins where exactly three of the digits are the same and none of the remaining digits may be repeated can be calculated using the formula 10^6 * 10. The first part is 10^6, which is taking 10 (the number of digits available) to the power of 6 (the number of digits that must be different). This means that each of the 6 digits that must be different can be any of the 10 digits available. The second part is the multiplication of 10 (the number of digits available). This is to represent the fact that the remaining three digits can be any of the 10 digits available, and none of them can be repeated. Finally, the result of 10^6 * 10 is 3,628,800, which is the number of different 9-digit pins where exactly three of the digits are the same and none of the remaining digits may be repeated.
Learn more about repeating number here
https://brainly.com/question/607253
#SPJ4
how many solutions are there to square root x =9
Answers
Answer:
There are 2 solutions to square root x = 9
They are 3, and -3
Step-by-step explanation:
The square root of x=9 has 2 solutions,
The square root means, for a given number, (in our case 9) what number times itself equals the given number,
Or, squaring (i.e multiplying with itself) what number would give the given number,
so, we have to find the solutions to \(\sqrt{9}\)
since we know that,
\((3)(3) = 9\\and,\\(-3)(-3) = 9\)
hence if we square either 3 or -3, we get 9
Hence the solutions are 3, and -3
Prove or disprove that the point (5,11−−√)(5,11) lies on the circle centered at the origin and containing the point (2,5√)(2,5).
Answers
The point does not lie on the center of the circle.
The point (5, 11) does not lie on the circle centered at the origin and containing the point (2, 5√).
The center of the circle in question is the origin (0, 0). The point (2, 5√) lies on the circle, so we need to check if the distance between the origin and (5, 11) is equal to the radius.
To determine if a point lies on a circle, we can calculate the distance between the center of the circle and the given point. If the distance is equal to the radius of the circle, then the point lies on the circle.
The distance between two points in a coordinate plane can be calculated using the distance formula: d = sqrt((x2 - x1)^2 + (y2 - y1)^2).
Calculating the distance between the origin and (5, 11), we have:
d = sqrt((5 - 0)^2 + (11 - 0)^2) = sqrt(25 + 121) = sqrt(146)=12.083.
Since the distance, sqrt(146), is not equal to the radius of the circle, the point (5, 11) does not lie on the circle centered at the origin and containing the point (2, 5√).
Learn more about Circle origin here:
brainly.com/question/1402846
#SPJ11
in the morning, the train went 170 miles. in the afternoon the train went 50 more miles. how far did the train end up going?
Answers
In the morning, the train went 170 miles. in the afternoon the train went 50 more miles. The Train ended up going 220 miles in total.
In the morning, the train traveled 170 miles.
In the afternoon, it traveled an additional 50 miles.
To find the total distance traveled by the train, we need to add the distance traveled in the morning and the distance traveled in the afternoon:
Total distance = Distance traveled in the morning + Distance traveled in the afternoon
Total distance = 170 miles + 50 miles
Total distance = 220 miles
So, the train ended up traveling a total of 220 miles.
To learn more about trains click on,
https://brainly.com/question/29326122
#SPJ4
What is the inverse of the function f(x) = 64x2 when x 2 0?

Answers
Answer:
The answer is A.
Y=64x²
X=64y²
X/64=y2
Then y = + or - root of x /8
Kareem rented a truck for one day. There was a base fee of $17.99, and there was an additional charge of 91 cents for each mile driven. Kareem had to pay
$206.36 when he returned the truck. For how many miles did he drive the truck?
Answers
Suppose a firm can sell it's output at p per unit and that its production function is given by y = AK∝Lβ, where K > 0 is capital input measured in machine-hours, L > 0 is labor input measured in worker-hours and A,∝, ß > 0 are parameters. The firm is perfectly competitive and the factor prices are r per hour and w per hour. (a) Show by partial differentiation that the production function has the property of increasing marginal productivity of capital (if ∝ > 1) and of labor (if ß > 1). Explain the economic significance of this. Does it explain why we normally assume that a and 3 are less than 1?
Answers
Increasing marginal productivity infers that extra units of capital and labor contribute more to yield, driving productive asset allotment. ∝ and ß < 1 expect reducing returns, adjusting with reality.
The production function has the property of increasing the marginal productivity of capital through Partial Differentiation.To appear that the generation work has to expand the marginal productivity of capital (in case ∝ > 1) and labor (on the off chance that ß > 1), we ought to take fractional subsidiaries with regard to each input calculation. For capital (K), the fractional subsidiary of the generation work is:
\(\dfrac{dy}{dK }= \alpha AK^{(\alpha-1)}L^\beta\)
Since ∝ > 1, (∝ - 1) is positive, which implies that the fractional subordinate \(\dfrac{dy}{dK}\) is positive. This shows that an increment in capital input (K) leads to an increment in yield (y), appearing to expand the marginal efficiency of capital.
Additionally, for labor (L), the fractional subordinate of the generation work is:
\(\dfrac{dy}{dL} = \beta AK^{\alpha}L^{(\beta-1)}\)
Since \(\mathbf{\beta > 1, (\beta-1)}\) it is positive, which implies that the halfway subordinate \(\dfrac{dy}{dL}\) is positive. This demonstrates that an increment in labor input (L) leads to an increment in yield (y), appearing to increase the marginal productivity
The economic importance of increasing marginal productivity is that extra units of capital and labor contribute more to yield as their amounts increment. This suggests that the more capital and labor a firm employments, the higher the rate of increment in yield. This relationship is vital for deciding the ideal assignment of assets and maximizing generation effectiveness.
In most generation capacities, it is accepted that ∝ and ß are less than 1. This presumption adjusts with experimental perceptions and financial hypotheses.
In case ∝ or ß were more prominent than 1, it would suggest that the marginal efficiency of the respective factor increments without bound as the calculated input increments.
In any case, there are decreasing returns to scale, which suggests that as calculated inputs increment, the Marginal efficiency tends to diminish. Therefore, accepting ∝ and ß are less than 1 permits for more reasonable modeling of generation forms and adjusts with the concept of diminishing marginal returns.
Learn more about the Marginal productivity of capital here:
https://brainly.com/question/18492635
#SPJ4
Totsakan bought one can of pineapple chunks for $2. How many cans can Stefan buy if he has $16?
Answers
Answer: she can buy 8 more pineapple chunks
Step-by-step explanation:
Simplify give ur answer in index form.

Answers
\( \frac{( {j}^{4} \: \times \: {j}^{8}) ^{3} }{( {j}^{9} \: \div \: {j}^{2}) ^{2} } \)
First we calculate the product of the denominator.\( \frac{( {j}^{12}) ^{3} }{( {j}^{9} \: \div \: {j}^{2}) ^{2} } \)
Then we calculate the quotient of the numerator.\( \frac{( {j}^{12}) ^{3} }{( {j}^{7}) ^{2} } \)
We multiply the exponents of the expression.\( \frac{ {j}^{36} }{ {j}^{14} } \)
We divide.\( \boxed{ \bold{ {j}^{22} }}\)
MissSpanishDetermine if the function below is continuous.OA. not continuous, 1 holeOB. continuousOC. not continuous, 2 holesD. not continuous, >2 holesC
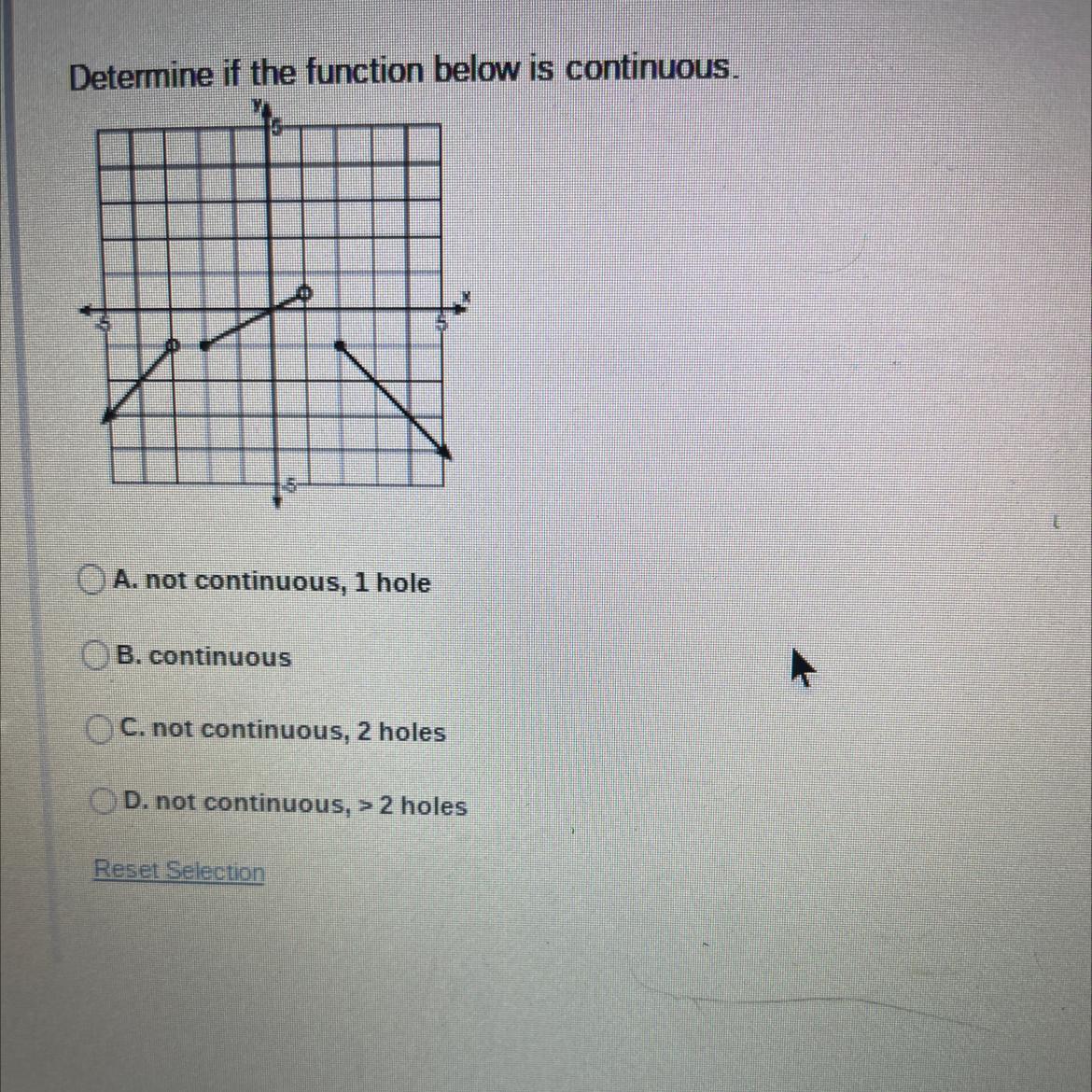
Answers
SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Answer the question
It can be seen that there are two breaks on the given graphs.
Hence, the answer is:
not continuous, 2 holes
the time to complete a bridge varies inversely with the square root of the number of people working. if 9 people can complete the job in 75 days then how long would it take 25 people?
Answers
If 09 people can complete the job in 75 days then 25 people needs 45 days to complete the job.
Let T be the time and L be the Labor (Number of people working on the bridge).
T ∞ 1/√L (Inverse relationship)
T = K/√L ----------------------------- (1)
Since, Constant "K" is introduced once the variation sign (∞) changes to equality (=) sign.
According to the question,
Time (T) = 75 days and
labor (L) = 09
From the equation (1), we get,
T = K / √L
⇒ 75 = K/√9
⇒ 75= K/3
⇒ K= 225
First, the relationship between these variables is:
T = 225/√L
Therefore, how long it will take 25 people to do it means that we should look for the time.
T=225/√L
⇒ T= 225/√25
⇒ T= 225/5
⇒ T= 45 days.
therefore, 25 people needs 45 days to complete the job.
Learn more about inverse relation :
https://brainly.com/question/1675160
#SPJ4
The equation y=5+0.5x represents the cost of getting a car wash and using the vacuum for x minutes. What is the y-intercept?
Answers
Answer:
The y intercept is 5. Usually, this is the number that is by itself with no variable by it. Ex: y= 5x + 4. 4 would be the y intercept.
Step-by-step explanation:
redo the probability calculation for pits in [1,3] and [2,2], assuming that each square contains a pit with probability 0.01, independent of the other squares. what can you say about the relative performance of a logical versus a probabilistic agent in this case?
Answers
The pit [2, 2]'s prior probability tends to be 0 and its posterior probability tends to be 1.
Compute the probabilities of Pits Each square in the Wumpus world do consist of a pit with the probability of 0.01 and consist of independent contents of the squares.
As suppose there are total of N/2 pits that are scattered randomly among the total of N squares. To compute the probabilities of the pits in [1, 3] and [2,2], consider that the probabilities of the assignments to complete where the other assignments doesn't gets off.
Thus, the total number of the 3-pit assignment rather remains consistent with the three assigned partial assignments here P 1,3 =true.Thus, in 21 assignment completes when the P 1,3 =true. Next the 55 assignment completes when the
P 1,3, = false.
Thus, it gives P(P 1.3 ) = a' (0.01(0.0001+0.0099+0.0099), 0.99(0.0001+ 0.0099)) = (0.1674, 0.8326)
While when the value of Pay = true, then there are basically four assignments that are partialenough with the total value of 0.0001, 0.0099, 0.0099, 0.9801, through the assignment gets completed.
Next when the value of Pa, = false, then there is only a single assignment that is partial with the value of 0.0001 that completes the assignments. Thus, then the final value of P (P2.2 ) is given asP(P2.2) = a' (0.01(0.0001+ 0.0099+0.0099+0.9801), 0.99x 0.0001) = (0.9902, 0.0098
Thus, the prior probability of the pit [2, 2] tends to be 0 and the posterior probability tends to be one (1).
Learn more about probability :
https://brainly.com/question/14915464
#SPJ4
Chadwick drives into the city to buy the most recent issue of black panther at a comic book store. On the way there he drove 15 mph. With less traffic on his return home, he drove 25 mph. If the entire travel time took him four hours, how long did it take him to get to the comic book store? Enter your answer in hours and rounded to one decimal place if needed.
Answers
Since the rule of distance is
\(d=v\times t\)Where v is the speed and t is the time
Since the distance from home to the book store is equal to the distance from the book store to the home, then
Let the distance = d
Since the speed in the going way is 15 mph, then
\(t_1=\frac{d}{15}\)Since the speed in the back way is 25 mph, then
\(t_2=\frac{d}{25}\)Since the time of the entire trip is 4 hours, then
\(t_1+t_2=4\)Substitute the values of t1 and t2
\(\frac{d}{15}+\frac{d}{25}=4\)Multiply both sides by 75 (L.C.M of 15 and 25)
\(\begin{gathered} \frac{d}{15}(75)+\frac{d}{25}(75)=4(75) \\ 5d+3d=300 \\ 8d=300 \end{gathered}\)Divide both sides by 8
\(\begin{gathered} \frac{8d}{8}=\frac{300}{8} \\ d=37.5m \end{gathered}\)Substitute d by 37.5 in t1 to find it
\(\begin{gathered} t_1=\frac{37.5}{15} \\ t_1=2.5h \end{gathered}\)It took him 2.5 hours to get to the book store
Equivalent expression
9(r + r + r+ r)
Answers
Answer:
=9*4r
=36r
Step-by-step explanation:
36r is the answer
Answer:
9 x r
9 x r
9 x r
9 x r
9r + 9r + 9r + 9r = 36r
The growth rate of the sunflower from day 14 to day
35 is nearly constant. On this interval, which
of the
following equations best models
the height k in
centimeters, of the sunflower t days after it begins
to grow?
Answers
Answer:
sorry I don't know.....