At a concession stand, one hot dog and one hamburger cost $3.75 ; one hot dog and cost $12.25 . Find the cost of one hot dog and the cost of one hamburger .
Answers
The function shows that the cost of hotdogs is 1.75 and the cost of hamburger is 1.5.
How to calculate the information?Let hotdogs = h
Let hamburger = x
The expression will be:
h + x = 3.25
h + 7x = 12.25
Subtract the functions
6x = 9
x = 1.5
Therefore, hot dogs will be:
= 3.25 - 1.5
= 1.75
Learn more about expressions on:
brainly.com/question/723406
#SPJ1
At a concession stand, one hot dog and one hamburger cost $3.25; one hot dog and seven hamburger cost $12.25. Find the cost of one hotdog and the cost of one hamburger.
Related Questions
b) Determine a parameterization for both of the following curves: a line segment connecting two points of your choice and half of a circle centered at the origin. c) Determine a parameterization for two of the following common surfaces: plane, sphere, (circular) paraboloid, (circular) cylinder, and half cone (choose only 2!).
Answers
b. r(t) = (cos(t), sin(t)), for 0 <= t <= pi. c. Sphere of radius 1 centered at the origin: r(u, v) = (cos(u) * sin(v), sin(u) * sin(v), cos(v)), for 0 <= u <= 2pi and 0 <= v <= pi.
b) Here are the parameterizations for a line segment connecting two points of your choice and half of a circle centered at the origin:
Line segment from (0, 0) to (1, 2): r(t) = (1 - t) * (0, 0) + t * (1, 2) = (t, 2t), for 0 <= t <= 1.
Half of a circle of radius 1 centered at the origin: r(t) = (cos(t), sin(t)), for 0 <= t <= pi.
c) Here are the parameterizations for a plane and a sphere:
Plane passing through (1, 0, 0), (0, 1, 0), and (0, 0, 1): r(u, v) = u * (1, 0, 0) + v * (0, 1, 0) + (1 - u - v) * (0, 0, 1), for 0 <= u <= 1 and 0 <= v <= 1.
Sphere of radius 1 centered at the origin: r(u, v) = (cos(u) * sin(v), sin(u) * sin(v), cos(v)), for 0 <= u <= 2pi and 0 <= v <= pi.
Note that for the plane parameterization, we used the fact that a plane passing through three non-collinear points can be parameterized by a linear combination of the points, with the coefficients summing to 1. For the sphere parameterization, we used spherical coordinates to express the position of each point on the sphere in terms of two angles, u and v.
Learn more about radius here
https://brainly.com/question/27696929
#SPJ11
Which equation represents a line that passes through the point (10, 7) and is perpendicular to the graph of the equation y = 5x − 4?
Answers
Answer:
y = - \(\frac{1}{5}\) x + 9
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = 5x - 4 ← is in slope- intercept form
with slope m = 5
given a line with slope m then the slope of a line perpendicular to it is
\(m_{perpendicular}\) = - \(\frac{1}{m}\) = - \(\frac{1}{5}\) , then
y = - \(\frac{1}{5}\) x + c ← is the partial equation
to find c substitute (10, 7 ) into the partial equation
7 = - \(\frac{1}{5}\) (10) + c = - 2 + c ( add 2 to both sides )
9 = c
y = - \(\frac{1}{5}\) x + 9 ← equation of perpendicular line
The gradient of the perpendicular line is -0.2
y = -0.2x + c
To find c, you have to substitute the x and y values, which are from the point given (10,7)
7 = -0.2(10) +c
7 + 2 = c
c = 9
y = -0.2x + 9
a student is working in an optics lab and has a light bulb which is 90 cm from a screen. She needs to make a real image of the bulb on the screen and shehas a positive lens witha focal length of 12.5 cm. Find two places she can put the lens andgive object and imagedistances to both setups.
Answers
The two places she can put lens and give object and image distances are 15cm and 75cm.
The Lens equation gives us:
1/f = 1/u + 1/v
From the problem we know that,
v=90-u
By solving
u² - 90u + 1125 = 0.
An optical system's focal length, which is the inverse of the system's optical power, indicates how strongly the system converges or diverges light. A system with a positive focal length is said to converge light, and one with a negative focal length is said to diverge light.
A negative focal length, on the other hand, indicates how far in front of the lens a point source must be located to form a collimated beam, for the special case of a thin lens in air, where a positive focal length is the distance over which initially collimated (parallel) rays are brought to a focus. For more generic optical systems, the focal length is merely the inverse of optical power and lacks any intuitive significance.
To learn more about Focal length :
https://brainly.com/question/28039799
#SPJ4
Factor out the greatet common factor. If the greatet common factor i 1, jut retype the polynomial. 16k3–4k2
Answers
The greatest common factor will be = 4k²
What is Factor?
A number or algebraic expression that divides another number or expression evenly—that is, without leaving any remainder. 3 and 6 are factors of 12 because 12 3 = 4 precisely and 12 6 = 2 precisely. The other 12 factors are 1, 2, 4, and 12.
Given,
polynomial = 16k³-4k²
= (4*4)k³ - (4k²) --- Factored by 4 *4
=4 (4k³) - 4k² --- associative property of multiplication
= 4( 4k²*k) - 4k² --- factored k³ as k² *k
= 4k² (k -4)---- commutative property of multiplication
The greatest common factor will be = 4k²
To learn more about polynomial visit:
brainly.com/question/11536910
#SPJ4
Which answer choice is it???
A 41
B 83
C 13
D 139

Answers
Describe the long run behavior of f(x)=5(2)x+1:
As x→−[infinity], f(x) =
As x→[infinity], f(x) =
Answers
The long run behavior of the function f(x)=5(2)x+1 is that it approaches 1 as x approaches negative infinity and it approaches infinity as x approaches positive infinity.
The long-term behavior of the function f(x)=5(2)x+1 can be discovered by examining how the function behaves as x gets closer to negative and positive infinity.
As x→−[infinity], f(x) = 5(2)^ -∞+1 = 5(0)+1 = 1
As x approaches negative infinity, the value of the function approaches 1.
As x→[infinity], f(x) = 5(2)^ ∞+1 = 5(∞)+1 = ∞
As x approaches positive infinity, the value of the function approaches infinity.
As a result, the function f(x)=5(2)x+1 behaves in the long run in such a way that it approaches 1 as x approaches negative infinity and infinity as x approaches positive infinity.
Learn more about behavior at https://brainly.com/question/22443880
#SPJ11
What is the value of the expression?
2 (32 – (4 - 1)"
Answers
How to solve this math problem?

Answers

Help! Please I need an answer fast!

Answers
The median wait time for the speed slide is 2 times longer than the median wait time for the wave machine.
No, There is a lot of overlap between the two data sets.
We have,
Box plots:
Speed side
Median = 11
First quartile = 6
Third quartile = 12
IQR = 12 - 6 = 6
Wave machine
Median = 9
First quartile = 8
Third quartile = 14
IQR = 14 - 8 = 6
Now,
Difference between the median.
= 11 - 9
= 2
Now,
From the box plots, the wait time for the wave machine is longer than the speed side.
Thus,
The median wait time for the speed slide is 2 times longer than the median wait time for the wave machine.
No, There is a lot of overlap between the two data sets.
Learn more about the median here:
https://brainly.com/question/28060453
#SPJ1
the product of a number and 4
Answers
Answer:
4n or n × 4
Step-by-step explanation:
Product means the result of multiplying factors.
Factors are the numbers or variables (a number, unknown) that are multiplied.
What is the value of the expression 6( -5 1/4 ?
Answers
Answer:
-63/2
Step-by-step explanation:
6( -5 1/4)
= 6(-21/4)
= -63/2
Its not a quiz/test its homework thats due in a bit :)
Just to clear any misunderstandings that might arise

Answers
Step-by-step explanation:
\( \underline{ \underline{ \text{Given}} }: \)
Coordinates of E = ( -3 , 2 )Coordinates of H = ( 1 , -1 )\( \underline{ \underline{ \text{To \: find}}} : \)
Midpoint of EHLet E ( -3 , 2 ) be ( x₁ , y₁ ) & H ( 1 , -1 ) be ( x₂ , y₂ )
\( \underline{ \underline{ \text{Solution}}} : \)
\( \sf{Midpoint = ( \frac{x_{1} + x_{2}}{2} \: , \frac{ y_{1} + y_{2}}{2} )}\)
⟶ \( \sf{( \frac{-3 + 1}{2} \: , \frac{2 + ( - 1)}{2} )}\)
⟶ \( \sf{( \frac{-2}{2} \:, \frac{2 - 1}{2} )}\)
⟶ \( \sf{( -1 \: ,\frac{1}{2} )}\)
\( \pink{ \boxed{ \boxed{ \tt{Our \: final \: answer : \boxed{ \underline{ \tt{(-1 \: , \: \frac{1}{2} )}}}}}}}\)
Hope I helped ! ♡
Have a wonderful day / night ! ツ
▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔
Problem 2:
The lifespan of a particular brand of light bulb follows a normal distribution with a mean of 1000 hours and a standard deviation of 50 hours.
Find:
a) the z-score of light bulb with a mean of 500 hours.
b) If a customer buys 20 of these light bulbs, what is the probability that the average lifespan of these bulbs will be less than 980 hours?
c) the probability of light bulbs with the mean of 400 hours.
d) the number of light bulbs with the mean less than 1000 hours
Answers
The answers are:
a) The z-score for a light bulb that lasts 500 hours is -10.
b) For a sample of 20 light bulbs, the probability that the average lifespan will be less than 980 hours is approximately 0.0367, or 3.67%.
c) The z-score for a light bulb that lasts 400 hours is -12. This is even more unusual than a lifespan of 500 hours.
d) Given the lifespan follows a normal distribution with a mean of 1000 hours, 50% of the light bulbs will have a lifespan less than 1000 hours.
How to solve the problema) The z-score is calculated as:
z = (X - μ) / σ
Where X is the data point, μ is the mean, and σ is the standard deviation. Here, X = 500 hours, μ = 1000 hours, and σ = 50 hours. So,
z = (500 - 1000) / 50 = -10.
The z-score for a bulb that lasts 500 hours is -10. This is far from the mean, indicating that a bulb lasting only 500 hours is very unusual for this brand of bulbs.
b) If a customer buys 20 of these light bulbs, we're now interested in the average lifespan of these bulbs. . In this case, n = 20, so the standard error is
50/√20
≈ 11.18 hours.
z = (980 - 1000) / 11.18 ≈ -1.79.
The probability that z is less than -1.79 is approximately 0.0367, or 3.67%.
c) The z-score for a bulb with a lifespan of 400 hours can be calculated as:
z = (400 - 1000) / 50 = -12.
The probability associated with z = -12 is virtually zero. So the probability of getting a bulb with a mean lifespan of 400 hours is virtually zero.
d) The mean lifespan is 1000 hours, so half of the light bulbs will have a lifespan less than 1000 hours. Since the lifespan follows a normal distribution, the mean, median, and mode are the same. So, 50% of light bulbs will have a lifespan less than 1000 hours.
Read more on probability here:https://brainly.com/question/13604758
#SPJ1
A circular disc has a diameter of 24 cm. What is the area of the disc?

Answers
Answer:
not 24 i got an 80 its not 24 though
Step-by-step explanation:
i dont know how this helps but there you go
NEED THE ANSWER ASAP!

Answers
Answer:
my nut is ytellow
Step-by-step explanation:
find the equation of the line parallel to H passes through (-4,2)

Answers
Answer:
y = \(\frac{1}{3}\) x + \(\frac{10}{3}\)
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
Calculate the slope m of H using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (0, - 3) and (x₂, y₂ ) = (3, - 2) ← 2 points on the line
m = \(\frac{-2+3}{3-0}\) = \(\frac{1}{3}\)
Parallel lines have equal slopes, thus
y = \(\frac{1}{3}\) x + c ← is the partial equation
To find c substitute (- 4, 2) into the partial equation
2 = - \(\frac{4}{3}\) + c ⇒ c = 2 + \(\frac{4}{3}\) = \(\frac{10}{3}\)
y = \(\frac{1}{3}\) x + \(\frac{10}{3}\) ← equation of parallel line
ASAP!! ITS URGENT
Find the lateral area, total area, and volume of each right circular come.

Answers
Answer:
58.
\(135\pi \: {km}^{2} \)
59.
\(216\pi \: {km}^{2} \)
60.
\(324 \: {km}^{3} \)
61.
\(72 \sqrt{5 } \pi \: {m}^{2} \)
62.
\(72( \sqrt{5} + 2)\pi \: {m}^{2}\)
63.
\(240\pi \: {m}^{3} \)
Step-by-step explanation:
58. First, we have to find the length of the cone shaper by using the Pythagorean theorem:
\( {l}^{2} = {12}^{2} + {9}^{2} = 144 + 81 = 225\)
\(l > 0\)
\(l = \sqrt{225} = 15 \: km\)
Now, let's find the lateral surface (r = 9 km):
\(a(lateral) = \pi \times r \times l = \pi \times 9 \times 15 = 135\pi \: {km}^{2} \)
59. The area of total surface is equal to a lateral surface's and base surface's sum:
Let's find the area of the base first:
\(a(base) = \pi \times {r}^{2} = {9}^{2} \times \pi = 81\pi \: {km}^{2} \)
Now, let's find the area of total surface:
\(a(total) = 135\pi + 81\pi = 216\pi\: {km}^{2} \)
60. h = 12 km
\(v = \frac{1}{3} \times a(base) \times h = \frac{1}{3} \times 81\pi \times 12 = 324\pi \: {km}^{3} \)
61. r = 12m
h = 5m
Let's find the length of the cone shaper by using the Pythagorean theorem:
\( {l}^{2} = {12}^{2} + {6}^{2} = 144 + 36 = 180\)
\(l > 0\)
\(l = \sqrt{180} = 6 \sqrt{5} \: m\)
Now, let's find the area of the lateral surface:
\(a(lateral) = \pi \times r \times l = \pi \times 12 \times 6 \sqrt{5} = 72 \sqrt{5} \pi \: {m}^{2} \)
62.
\(a(base) = \pi \times {r}^{2} = 144\pi \: {m}^{2} \)
\(a(total) = 72 \sqrt{5} \pi + 144\pi = 72( \sqrt{5} + 2)\pi \: {m}^{2} \)
63.
\(v = \frac{1}{3} \times a(base) \times h = \frac{1}{3} \times 144\pi \times 5 = 240\pi \: {m}^{3} \)
I don't know if these answer are correct, though...
if Billy has 23 chairs and the sun is orange on Tuesdays, what color is Sarah's hair at 2:73 in the morning if she eats a candle 1 hour and 26 minutes before 2:73am?
Answers
Answer:
I think the answer is Africa, I dunno.
Step-by-step explanation:
10) Apply the distributive property to factor out the greatest common factor. 35 + 50 = **Write in the form __(__+__) *
__________
Answers
Answer:
its 85 ...................
(v) test the hypothesis that women with above average looks earn the same average logwage as women with below average looks. use a significance level of 5%. (2 points) this hypothesis states that b2
Answers
The evidence does not strongly support the claim that women with above-average looks earn significantly more than women with average looks.
To understand the findings, we need to discuss a few key concepts. First, let's clarify the null hypothesis (H0) and the alternative hypothesis (H1). In this case, the null hypothesis states that there is no relationship between physical appearance and income (β2 = 0), while the alternative hypothesis suggests that there is a relationship (β2 ≠ 0).
In this scenario, the one-sided p-value of 0.272 means that there is a 27.2% chance of observing a relationship between physical appearance and income as strong or stronger than what was found in the study, purely by chance, if there is actually no relationship (β2 = 0). Since this p-value is relatively high (greater than the commonly used threshold of 0.05), it implies weak evidence against the null hypothesis.
Therefore, based on the given information, the evidence does not provide sufficient statistical support to reject the null hypothesis that there is no relationship between physical appearance and income (H0: β2 = 0).
To know more about hypothesis here
https://brainly.com/question/29576929
#SPJ4
Which line is a line of symmetry for the figure below?
A.
Line A
B.
Line C
C.
Line D
D.
Line B

Answers
Answer:
A.
Line A
Please mark my answer the brainliestA project has an initial cost of $30 million.The project is expected to generate a cash flow of $2.85 million at the end of the first year.All the subsequent cash flows will grow at a constant growth rate of 3.85% forever in future.If the appropriate discount rate of the project is 11%,what is the profitability index of the project? a.1.917 b.1.328 c.1.387 d.1.114 ortcehov e. None of the above
Answers
Profitability index is 1.387. Thus, the correct option is (c) 1.387.
The formula for calculating the profitability index is:
P.I = PV of Future Cash Flows / Initial Investment
Where,
P.I is the profitability index
PV is the present value of future cash flows
The initial investment in the project is $30 million. The cash flow at the end of the first year is $2.85 million.
The present value of cash flows can be calculated using the formula:
PV = CF / (1 + r)ⁿ
Where,
PV is the present value of cash flows
CF is the cash flow in the given period
r is the discount rate
n is the number of periods
For the first-year cash flow, n = 1, CF = $2.85 million, and r = 11%.
Substituting the values, we get:
PV = 2.85 / (1 + 0.11)¹ = $2.56 million
To calculate the present value of all future cash flows, we can use the formula:
PV = CF / (r - g)
Where,
PV is the present value of cash flows
CF is the cash flow in the given period
r is the discount rate
g is the constant growth rate
For the subsequent years, CF = $2.85 million, r = 11%, and g = 3.85%.
Substituting the values, we get:
PV = 2.85 / (0.11 - 0.0385) = $39.90 million
The total present value of cash flows is the sum of the present value of the first-year cash flow and the present value of all future cash flows.
PV of future cash flows = $39.90 million + $2.56 million = $42.46 million
Profitability index (P.I) = PV of future cash flows / Initial investment
= 42.46 / 30
= 1.387
Therefore, the correct option is (c) 1.387.
Learn more about Profitability index
https://brainly.com/question/30641835
#SPJ11
The line plot displays the cost of used books in dollars.
A horizontal line starting at 1 with tick marks every one unit up to 9. The line is labeled Cost in Dollars, and the graph is titled Cost of Used Books. There is one dot above 2, 4, 8, and 9.There are two dots above 6 and 7. There are three dots above 3.
Which measure of center is most appropriate to represent the data in the graph, and why?
Answers
The mode is the most appropriate measure of center to represent the data in the graph because it reflects the most common value(s) observed in the dataset. In this case, the mode is 3.
The most appropriate measure of center to represent the data in the given line plot is the mode.
The mode is the value or values that occur most frequently in a dataset. In this case, we can observe the frequencies of the data points on the line plot:
There is one dot above 2, 4, 8, and 9.
There are two dots above 6 and 7.
There are three dots above 3.
Based on this information, the mode(s) of the dataset would be the values that have the highest frequency. In this case, the mode is 3 because it appears most frequently with a frequency of three. The other data points have frequencies of one or two.
The mode is particularly appropriate in this scenario because it represents the most common or frequently occurring value(s) in the dataset. It is useful for identifying the central tendency when the data is discrete and there are distinct peaks or clusters.
While the median and mean are also measures of center, they may not be the most appropriate in this case. The median represents the middle value and is useful when the data is ordered. However, the given line plot does not provide an ordered arrangement of the data points. The mean, on the other hand, can be affected by outliers and extreme values, which may not accurately represent the central tendency of the dataset in this scenario.
Therefore, the mode is the most appropriate measure of center to represent the data in the graph because it reflects the most common value(s) observed in the dataset. In this case, the mode is 3.
for such more question on measure of center
https://brainly.com/question/25716982
#SPJ8
Solve the following equation by completing the square
2x^2+4x=16
Answers
Answer:
x=2,-4
Step-by-step explanation:
expand and simplify 5m(5-n)+3m-7n
Answers
Step-by-step explanation:
25m -5mn +3m -7n
28m -5mn -7n
Answer:
13m-5mn-7n
Step-by-step explanation:
(5m×5)-(5m×n)+3m-7n
10m-5mn+3m-7n
collect like terms
10m+3m-5mn-7n
13m-5mn-7n
:)
Given the following coordinates complete the reflection transformation.

Answers
Answer:
For a general point (x, y), a reflection across the line x = a transforms the point into:
(a + (a - x), y) = (2a - x, y)
So if we first do a reflection across the line x = 1, the new point will be:
(2*1 - x, y) = (2 - x, y)
And if we now do a reflection across the line x = 3, the new point will be:
(2*3 - (2 - x), y) = (6 - 2 + x, y) = (4 + x, y)
Now that we have the general formula we can solve the question.
For the point (-5, 2)
The generated point after the reflections is:
(4 + (-5), 2) = (-1, 2)
For the point (-1, 5)
The generated point after the reflections is:
(4 + (-1), 5) = (3, 5)
For the point (0, 3)
The generated point after the reflections is:
(4 +0, 3) = (4, 3)
PLEASE HELP ME WITH THIS QUESTION
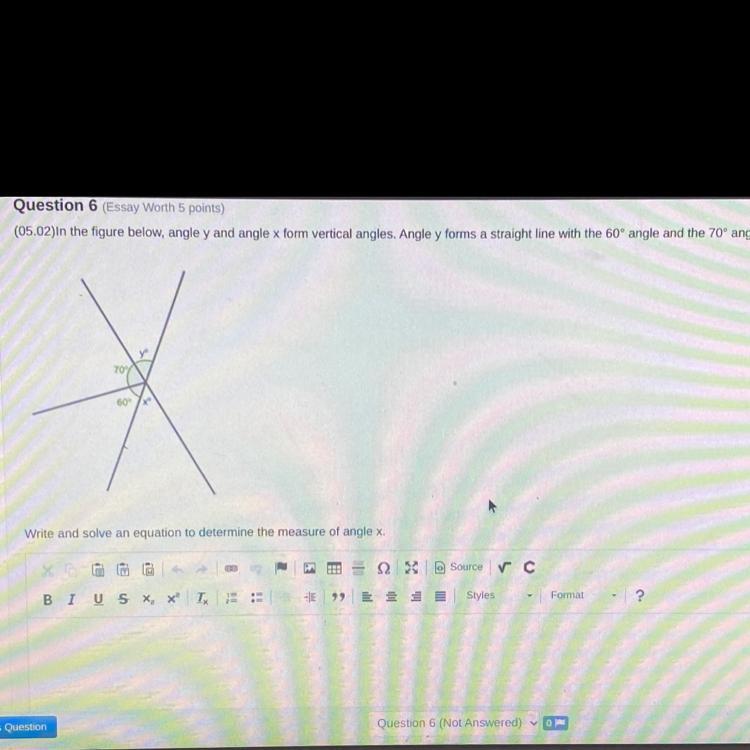
Answers
Y =50, vertical angles are congruent
X=50 degrees
Help please???????????

Answers
Answer:
525
Step-by-step explanation:
i really dont know what it asking
according to a recent study conducted by businessmen, 16% of all shareholders have some college education. suppose that 47% of all adults have some college education and that 52% of all adults are shareholders. for a randomly selected adult: 1. what is the probability that the person did not own shares of stock?
Answers
To answer this question, we need to use the information given in the problem. We know that 52% of all adults are shareholders, so the probability that a randomly selected adult owns shares of stock is 0.52.
To find the probability that a randomly selected adult did not own shares of stock, we can subtract this probability from 1 (since the sum of the probabilities of all possible outcomes must equal 1).
So, the probability that a randomly selected adult did not own shares of stock is:
1 - 0.52 = 0.48
Now, we can see that the information about shareholders having some college education is not needed to answer this question.
Learn more about Probability at: https://brainly.com/question/25839839
#SPJ11
A toy store marks down every toy by 15% in June .how much does a toy cost during June
Answers
Answer:
15% less than its regular price
Step-by-step explanation:
If the toy is marked down 15% in June, its cost during June is 15% less than its regular cost. (It will be 85% of its regular cost.)