at state college last term, 53 of the students in a physics course earned a's, 81 earned b's, 106 got c's, 85 were issued d's, and 64 failed the course. if this grade distribution was graphed on pie chart, how many degrees would be used to indicate the a region?
Answers
Step-by-step explanation:
'a' region is 53 out of (53+81+106+85 + 64 = 389)
53/389 ths of the 360 degree circle would be the a's
53/389 * 360 = 49 degrees
Related Questions
Angles A and B are complementary to each other. If mA = 23° and mzB = (4x + 15)°, find the value of x.
Ox=2
Ox=13
Ox= 35.5
Ox=67
Answers
Answer:
x = 13
Step-by-step explanation:
m∠A + m∠B = 90° complementary angles = 90°
m∠A = 23°
m∠B = (4x + 15)°
23 + 4x + 15 = 90
- 15 - 23 both sides = cancel out to make 4x the subject
4x = 52
÷ 4 both sides = get rid of coefficient (make x alone)
x = 13
Answer:
B) x = 13
Step-by-step explanation:
Complementary angles means that, when combined, they add up to 90°. In this case, the given Angles A & B are complementary, ∴
∠A + ∠B = 90°
It is given that:
m∠A = 23°
m∠B = (4x + 15)°
Plug in the corresponding terms to the corresponding variables:
m∠A + m∠B = 90°
(23)° + (4x + 15)° = 90°
First, combine like terms. Like terms are terms that share the same amount of the same variables:
4x + 15 + 23 = 90
4x + (15 + 23) = 90
4x + 38 = 90
Next, isolate the variable, x. Note the equal sign, what you do to one side, you do to the other. Do the opposite of PEMDAS.
PEMDAS is the order of operations, and stands for:
Parenthesis
Exponents (& Roots)
Multiplication
Division
Addition
Subtraction
~
First, subtract 38 from both sides of the equation:
4x + 38 = 90
4x + 38 (-38) = 90 (-38)
4x = 90 - 38
4x = 52
Next, divide 4 from both sides of the equation:
(4x)/4 = (52)/4
x = 52/4
x = 13.
B) x = 13 is your answer.
Check: Plug in 13 for x in the given angle measurements, and combine the angles to obtain the measurement 90° (complementary):
m∠B = (4x + 15)
m∠B = (4 * 13) + 15
m∠B = 52 + 15
m∠B = 67°
m∠A + m∠B = 90°
m∠A + (67) = 90°
m∠A + 67 (-67) = 90 (-67)
m∠A = 90 - 67
m∠A = 23°
~
Learn more about complementary angles, here:
https://brainly.com/question/13829049
programming exercise 3.21 uses zellers congruence to calculate the day of the week simplify listing 6.12 print calendar using zellers algorithm to get the start day of the mont
Answers
The Zeller’s congruence is an algorithm developed to calculate the day of the week is given below.
We know that Zeller's congruence is an algorithm that determines the day of the week for any given date.
First Take the month and subtract two from it if the month is January or February. Otherwise, leave the month unchanged.
Then Divide the result from step 1 by 12 and round down to the nearest integer. Call this value "C".
Divide the year by 4 and round down to the nearest integer. Call this value "Y".
Divide the year by 100 and round down to the nearest integer. Call this value "Z".
Divide the year by 400 and round down to the nearest integer. Call this value "X".
To Calculate the day of the week
(day + ((13 * A) - 1) / 5 + Y + Y / 4 + Z / 4 - 2 * Z + X) % 7
Where A is the result from step 1.
This formula will give a number between 0 and 6, where 0 represents Saturday, 1 represents Sunday, 2 represents Monday, and so on.
To print a calendar using Zeller's algorithm, we can first calculate the start day of the month using the algorithm above, and then use that information to print out the calendar for the entire month.
Tuesday Wednesday Thursday Friday Saturday Sunday Monday
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31
This calendar shows the days of the week along the top row and the dates of the month in the corresponding columns.
Learn more about Zellers congruence;
https://brainly.com/question/17646352
#SPJ4
select the correct answer





Answers
how many cards must be selected from a standard deck of 52 cards to guarantee that at least three cards of the same (matching) suit are chosen
Answers
Answer:
Step-by-step explanation:
17
Solve This question down below in the frame

Answers
The solution to the question \(-7 \frac{2}{3} + (-5\frac{1}{2} ) + 8\frac{3}{4}\) is \(-4\frac{5}{12}\).
To solve this problem, we need to add up all the given numbers. To make the addition process easier, we can convert all the mixed numbers into improper fractions first.
\(-7\frac{2}{3}\) =\(-(\frac{21+2}{3} )\)= \(-\frac{23}{3}\)
\(-5\frac{1}{2}\) = \(-(\frac{10+1}{2} )\)= \(-\frac{11}{2}\)
\(8\frac{3}{4}\) = \(\frac{32+3}{4}\) = \(\frac{35}{4}\)
Now we can add up the three fractions:
\(-\frac{23}{3}+ -\frac{11}{2}+\frac{35}{4}\)
We must choose a common denominator so that we can sum up these fractions. The smallest common multiple of 3, 2, and 4 is 12.
Therefore,
\(\frac{(-23*4)+(-11*6)+(35*3)}{12}\)
\(\frac{-92-66+105}{12} \\\frac{-53}{12}\)
Therefore, the solution is \(\frac{-53}{12}\). We can also convert this back into a mixed number if required:
\(\frac{-53}{12}\) = \(-\frac{(4*8+5)}{12}\) =\(-4\frac{5}{12}\).
So the final answer is \(-4\frac{5}{12}\).
To learn more about improper fractions, refer:-
https://brainly.com/question/21449807
#SPJ1
Krista made 8 gallons of juice to sell at the football game. She plans to put the juice in 1-quart containers, and pour each customer 1 pint of juice in a paper cup. How many containers and paper cups does she need for the 8 gallons of juice?
Answers
She would need 32 1-quart containers because 8 gallons is 32 quarts.
She would need 64 cups because there are 62 pints in 8 gallons.
evaluate this please

Answers
Answer:
17
Step-by-step explanation:
for f(6).
\(f(6) = - 3 \times 6 + 1 = 17\)
Answer:
17
Step-by-step explanation:
In a certain region, the probability of selecting an adult over 40 years of age with a certain disease is 0.04. If the probability of correctly diagnosing a person with this disease as having the disease is 0.78 and the probability of incorrectly diagnosing a person without the disease as having the disease is 0.05, what is the probability that an adult over 40 years of age is diagnosed with the disease? 4
The probability is
(Type an integer or a decimal. Do not round)
Answers
The probability that an adult over 40 years of age is diagnosed with the disease is approximately 0.314.
To find the probability that an adult over 40 years of age is diagnosed with the disease, we can use Bayes' theorem.
Let's define the events:
A: An adult over 40 years of age has the disease.
B: An adult over 40 years of age is diagnosed with the disease.
We are given the following probabilities:
P(A) = 0.04 (probability of an adult over 40 having the disease)
P(B|A) = 0.78 (probability of correctly diagnosing a person with the disease)
P(B|A') = 0.05 (probability of incorrectly diagnosing a person without the disease)
We want to find P(A|B), the probability of an adult over 40 having the disease given that they are diagnosed with the disease.
According to Bayes' theorem:
P(A|B) = (P(B|A) * P(A)) / P(B)
To calculate P(B), we can use the law of total probability:
P(B) = P(B|A) * P(A) + P(B|A') * P(A')
Since P(A') = 1 - P(A) (probability of not having the disease), we can substitute it into the equation:
P(B) = P(B|A) * P(A) + P(B|A') * (1 - P(A))
Plugging in the given values:
P(B) = 0.78 * 0.04 + 0.05 * (1 - 0.04)
Now we can calculate P(A|B) using Bayes' theorem:
P(A|B) = (P(B|A) * P(A)) / P(B)
P(A|B) = (0.78 * 0.04) / P(B)
Substituting the value of P(B) we calculated earlier:
P(A|B) = (0.78 * 0.04) / (0.78 * 0.04 + 0.05 * (1 - 0.04))
Calculating this expression:
P(A|B) ≈ 0.314
Learn more about probability here
https://brainly.com/question/31828911
#SPJ11
(From Unit 5, Lesson 11.)
3. A ramp is two meters long. Priya wants to investigate how the distance a basketball
rolls is related to the location on the ramp where it is released.
Recommend a way Priya can gather data to help understand this relationship.
Answers
To understand the relationship between the location on the ramp where the rolls are released and the distance they travel, Priya can gather data by conducting an experiment. She can release rolls from different locations on the ramp and measure the distance they travel in meters.
She can repeat this process multiple times for each location to ensure accuracy and gather enough data for analysis.
To make the experiment more controlled, Priya can keep the release force constant for each roll and use the same type of rolls throughout the experiment. Additionally, she can use a measuring tape or ruler to measure the distance traveled by each roll.
Once Priya gathers all the data, she can analyze it by creating a graph or chart to visually represent the relationship between the release location and the distance traveled. This will help her identify any patterns or trends and draw conclusions about the relationship.
Priya can set up an experiment following these steps:
1. Set up the ramp on a flat surface and ensure it is stable.
2. Use a measuring tape or ruler to measure and mark specific locations on the ramp in meters (e.g., every 0.5 meters). These will serve as the release points for the ball.
3. Choose a ball of consistent size and weight to roll down the ramp.
4. Begin by releasing the ball from the first marked location on the ramp (e.g., 0.5 meters). As the ball rolls, make sure to track its distance from the bottom of the ramp.
5. Use a measuring tape or ruler to measure the distance the ball traveled from the base of the ramp in meters. Record this measurement in a data table or notebook.
6. Repeat the experiment for the other marked locations on the ramp, carefully measuring and recording the distance the ball travels each time.
7. Conduct multiple trials at each release location to account for any variability in the data.
8. Analyze the data by comparing the release location (in meters) to the corresponding distance the ball traveled. This will help Priya understand the relationship between the ball's release location on the ramp and the distance it rolls.
Overall, conducting an experiment to gather data is an effective way for Priya to understand the relationship between the location on the ramp where rolls are released and the distance they travel in meters.
Learn more about Graphs here: brainly.com/question/24861666
#SPJ11
(6x^2) (4x^2)
nd some help
Answers
Answer:
So, I solved it and I got this:
Simplify the expression.
24 x^ 4
Step-by-step explanation:
hope this helps! have a great day!
How do you find the marginal pdf of a joint pdf?
Answers
To find the marginal pdf of a joint pdf, you must first integrate the joint pdf over the appropriate marginal domain.
To find the marginal pdf of a joint pdf, you need to integrate the joint pdf over all possible values of the other variable(s) in the joint distribution. For example, if you have a joint pdf for two variables X and Y, to find the marginal pdf of X, you integrate the joint pdf over all possible values of Y.
This will give you the pdf of X alone. Similarly, to find the marginal pdf of Y, you integrate the joint pdf over all possible values of X. This approach works for any number of variables in the joint distribution, and can be used to obtain the pdf of each variable individually.
You can learn more about marginal pdf at
https://brainly.com/question/30214799
#SPJ11
help! Will give Brainliest to the right answer!
Algebra!

Answers
Step-by-step explanation:
Horizontal asymptote is the same and vertical asymptote at x = 6 (B).
as part of a promotion, people who participate in a survey are sent a free coupon for one of three winter activities: skiing, snow tubing, or sleigh rides. participants have an equal chance of receiving each type of coupon. if 900 people participate, how many would be expected to receive a coupon for sleigh rides
Answers
It is expected that 300 participants out of the 900 who participate in the survey would receive a coupon for sleigh rides.
To determine the number of participants expected to receive a coupon for sleigh rides, we need to divide the total number of participants (900) by the number of coupon options (3) since each option has an equal chance of being received.
The expected number of participants receiving a coupon for sleigh rides can be calculated as follows:
Total participants / Number of coupon options = Expected number of participants receiving a sleigh ride coupon
900 participants / 3 coupon options = 300 participants.
Therefore, it is expected that 300 participants out of the 900 who participate in the survey would receive a coupon for sleigh rides.
It's important to note that this calculation assumes an equal chance of receiving each type of coupon and does not consider any specific preferences or biases that participants may have.
The calculation is based on the assumption of a random distribution of coupons among the participants.
For similar question on survey.
https://brainly.com/question/14610641
#SPJ11
1. Solve for x.
4x + 12 = 60
2. Solve for x.
2x + 5 = 21
3. Solve for x.
4x - 7 = 5
4. Solve for x.
3b - 4 = 11
5. Solve for x.
x3 = 33
6. Solve for x.
⅓ x + 6 = -8
7. Landon has 42 candies. He shares them with his friend Fred in a ratio of 3:5. How many candies does each person get?
8. Simplify the expression.
3x - 2 + 7 - 7x + 9
9. Simplify the expression.
⅓ (x - 3) + 12x
10. Jonah put in 12 colored tiles in a jar. There are 3 red tiles, 7 blue tiles, and 2 yellow tiles. What is the probability that he will select a red tile first, then select a blue tile next without replacing the first tile?
11. Tia is painting her house. She paints 34 ½ square feet in ¾ of an hour. At this rate, how many square feet can she paint each hour?
12. Sam raked 3 bags of leaves in 16 minutes. If he continues to work at the same rate, about how long will it take him to rake 5 bags?
Answers

1.)x=12 2.)x=8 3.)x=3 4.)x/b=5 5.)x=11 6.)x=-4 7.) about 25 8.)-4x+15 9.) 37/3 x +1 10.)63.74% chance 11.) 45 square feet 12.)26.66665
Hope this helps
Have a great day/night
How do you find the measure of each angle indicated? m

Answers
19x-20+16x-5 = 360
35x-25=360
Divide by 5
7x-5=72
7x=77
X=11
Then just plug in x for each angle! Hope this helps!
what is the definition for relation in math?
Answers
A relation in math is a set of ordered pairs containing two elements, one from each set. The first element is from the domain and the second from the range.
Relations can be expressed as a set of ordered pairs, as a graph, or as a mapping diagram. A function is a special type of relation in which, for every element in the domain, there is one and only one element in the range. This is expressed mathematically by stating that for every x in the domain, there is one and only one y in the range such that y = f(x). To calculate a relation, the domain and range values are paired with each other, and the ordered pairs are written down. For example, if the domain is {2,3,4,5} and the range is {7,8,9,10}, then the relation would be {(2,7),(3,8),(4,9),(5,10)}.
Learn more about range here:
https://brainly.com/question/16664109
#SPJ4
A cell phone company uses the equation C=$0.15t+$35.00 to determine the total cost, C, for a month of service based on the number of text messages, t. Identify the slope.
Answers
Slope is $0.15 of the equation of cost C=$0.15t+$35.00.
What is Slope of Line?The slope of the line is the ratio of the rise to the run, or rise divided by the run. It describes the steepness of line in the coordinate plane.
The slope intercept form of a line is y=mx+b, where m is slope and b is the y intercept.
The slope of line passing through two points (x₁, y₁) and (x₂, y₂) is
m=y₂-y₁/x₂-x₁
Given that A cell phone company uses the equation C=$0.15t+$35.00
C is the total cost for a month of service.
t is the number of text messages.
We have to find the slope of the equation.
slope is 0.15 and 35.00 is the y intercept of the equation given.
Hence, slope is $0.15 of the equation of cost C=$0.15t+$35.00.
To learn more on slope of line click:
https://brainly.com/question/14511992
#SPJ1
There are four students named A,B,C, and D. All four of them are loss averse over money, with the same value function for money: v(x dollars )={√x x ≥ 0
{-2√-x x < 0
All three of them are also loss averse over mugs, with the same value function for mugs:
v(y mugs)={3y y ≥ 0
{4y y < 0
Total utility is the sum of the gain/loss utility for mugs and the gain/loss utility for money. The reference point is the status quo, that is, a person's initial endowment. Student A owns a mug and is willing to sell it for a price of a dollars or more. Student B does not own a mug and is willing to pay up to b dollars for buying it. Student C does not own a mug and is indifferent between getting a mug and getting c dollars. Student D is indifferent between losing a mug and losing d dollars.
1. Solve for a,b,c, and d.
2. Instead, suppose A, B, C, and D are only loss averse over mugs, but not over money. That is, their value function for money is instead:
v(x dollars)={√x x ≥ 0
{-√-x x < 0
and their value function for mugs remains:
v(y mugs)={3y y ≥ 0
{4y y < 0
Solve for a,b,c, and d.
3. Instead, suppose A,B,C, and D are not loss averse:
v(x dollars)={√x x ≥ 0
{-√-x x < 0
and v(y mugs)=3y
Solve for a,b,c, and d.
4. Suppose A, B, C, and D are not loss averse (as in the previous question), but their value for a mug varies with ownership. Specifically, the value of the mug is 3 for someone who does not currently own the mug, and 4 for someone who currently owns a mug. Solve for a,b,c, and d.
Answers
As per the question, All four students A, B, C, and D are loss-averse over money and have the same value function as below:v(x dollars)={√x x ≥ 0 {-2√-x x < 0They are also loss averse over mugs and have the same value function.
v(y mugs)={3y y ≥ 0
{4y y < 0
Now, we have to find the values of a, b, c and d as below:
- Student A owns a mug and is willing to sell it for a price of a dollars or more. i.e v(a) = v(0) + v(a-A), where A is the initial endowment of A. According to the given function, v(0) = 0, v(a-A) = 3, and v(A) = 4.
So, a ≥ A+3/2
- Student B does not own a mug and is willing to pay up to b dollars for buying it. i.e v(B-b) = v(B) - v(0), where B is the initial endowment of B. According to the given function, v(0) = 0, v(B-b) = -4, and v(B) = -3.
So, b ≤ B+1/2
- Student C does not own a mug and is indifferent between getting a mug and getting c dollars. i.e v(c) = v(0) + v(c), where C is the initial endowment of C. According to the given function, v(0) = 0, v(c) = 3.
So, c = C/2
- Student D is indifferent between losing a mug and losing d dollars. i.e v(D-d) = v(D) - v(0), where D is the initial endowment of D. According to the given function, v(0) = 0, v(D-d) = -3.
So, d = D/2
2) In this case, value function for money changes to:v(x dollars)={√x x ≥ 0
{-√-x x < 0
However, the value function for mugs remains the same:v(y mugs)={3y y ≥ 0
{4y y < 0
Therefore, values for a, b, c, and d will remain the same as calculated in part (1).
3) In this case, students are not loss-averse. Value function for money:v(x dollars)={√x x ≥ 0
{-√-x x < 0
Value function for mugs:v(y mugs)={3y y ≥ 0
The reference point is the status quo, i.e initial endowment. So,
- Student A owns a mug and is willing to sell it for a price of a dollars or more. The value of mug for A is 3 initially and he would sell it for 3 or more.
So, a ≥ A+3/2
- Student B does not own a mug and is willing to pay up to b dollars for buying it. The value of mug for B is 3 initially and he would buy it for 3 or less.
So, b ≤ B+3/2
- Student C does not own a mug and is indifferent between getting a mug and getting c dollars. The value of the mug for C is 3 initially.
So, c = 3
- Student D is indifferent between losing a mug and losing d dollars. The value of the mug for D is 3 initially.
So, d = 3
4) In this case, value function for money:v(x dollars)={√x x ≥ 0
{-√-x x < 0
Value function for mugs: Mug will have a value of 4 for someone who owns it and 3 for someone who does not own it.
The reference point is the status quo, i.e initial endowment. So,
- Student A owns a mug and is willing to sell it for a price of a dollars or more. The value of mug for A is 4 initially and he would sell it for 4 or more.
So, a ≥ A+2
- Student B does not own a mug and is willing to pay up to b dollars for buying it. The value of mug for B is 3 initially and he would buy it for 3 or less.
So, b ≤ B+3/2
- Student C does not own a mug and is indifferent between getting a mug and getting c dollars. The value of the mug for C is 3 initially and he would like to buy it for 3.
So, c = 3
- Student D is indifferent between losing a mug and losing d dollars. The value of the mug for D is 3 initially.
So, d = 3.
To know more about students visit:
https://brainly.com/question/29101948
#SPJ11
A university official wants to determine if a relationship exists between whether students choose their majors before their junior year and whether they graduate from college. For this study, what is the response variable?
Answers
For this study, what is the response variable is b. Whether or not a student graduates from college.
The outcome of an experiment in which the explanatory variable is altered is the response variable. It is a variable whose variation can be accounted for by other variables. It is also known as the outcome variable or the dependent variable. As an illustration, the students wish to utilise height to predict age; hence, height is the explanatory variable and age is the response variable.
Whether a student in the example graduates from college. The university official is interested in examining this variable to see whether it has any associations with the predictor variable, which is whether students declare their majors before their junior year. A is the predictor variable. if a student chooses a major prior to entering their junior year.
Complete Question:
A university official wants to determine if a relationship exists between whether students choose their majors before their junior year and whether they graduate from college. For this study, what is the response variable?
a. Whether a student decides on his/her major before their junior year
b. Whether or not a student graduates from college.
Read more about response variable on:
https://brainly.com/question/22046153
#SPJ4
Which of the following could be an example of a function with a domain
(-∞0,00) and a range (-∞,4)? Check all that apply.
A. V = -(0.25)* - 4
-
□ B. V = − (0.25)*+4
c. V = (3)* +4
□ D. V = − (3)* — 4
-

Answers
The correct options that could be an example of a function with a domain (-∞0,00) and a range (-∞,4) are given below.Option A. V = -(0.25)x - 4 Option B. V = − (0.25)x+4
A function can be defined as a special relation where each input has exactly one output. The set of values that a function takes as input is known as the domain of the function. The set of all output values that are obtained by evaluating a function is known as the range of the function.
From the given options, only option A and option B are the functions that satisfy the condition.Both of the options are linear equations and graph of linear equation is always a straight line. By solving both of the given options, we will get the range as (-∞, 4) and domain as (-∞, 0).Hence, the correct options that could be an example of a function with a domain (-∞0,00) and a range (-∞,4) are option A and option B.
Know more about function here:
https://brainly.com/question/11624077
#SPJ8
Joe and Will both work as cooks at Burger Palace. Each prepares hamburgers at a different speed, as shown by the functions below: J(b) = 14b + 7 W(b) = 7b + 42 where b represents the number of hamburgers cooked and J(b) and W(b) represent the amount of time each cook takes in minutes. At what value of b will their cooking time be equivalent? A. B = 5 B. B = 19 C. B = 6 D. B = 12
Answers
Answer:
A. B = 5
Step-by-step explanation:
Joe:
J(b) = 14b + 7
Will:
W(b) = 7b + 42
Where,
b = number of hamburgers cooked
J(b) and W(b) = amount of time each cook takes in minutes respectively
At what value of b will their cooking time be equivalent?
Equate both functions
Joe = Will
14b + 7 = 7b + 42
Collect like terms
14b - 7b = 42 - 7
7b = 35
Divide both sides by 7
b = 35 / 7
= 5
b = 5
The answer is
A. B = 5
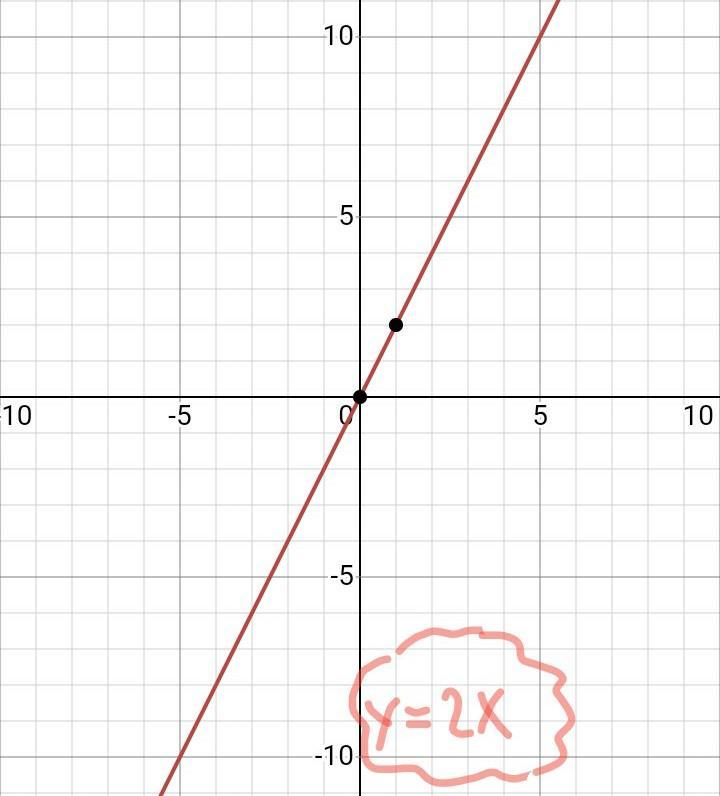
Please help due in a few minutes I will mark u brainliest

Answers
y = 4x - 5
How to:
y-intercept: -5
(remember, where it touches the y-axis)
Rise/Run
( It goes up 4 and over 1) 4/1= 4
Hope that helps :)
If f(x) = sin x + 2x + 1 and g is the inverse function of f, what is the value of g'(1) ?.
Answers
Answer:
1/3
Step-by-step explanation:
\(g(f(x))=x \\ \\ g'(f(x))f'(x)=1 \\ \\ g'(f(x))=\frac{1}{f'(x)} \\ \\ g'(f(x))=\frac{1}{\cos x+2} \\ \\ g'(f(0))=\frac{1}{\cos(0)+2} \\ \\ g'(1)=\frac{1}{3}\)
2. A town is planning a circular walkway that will be 2 meters wide. The walkway will have an inter radius of 5 meters with a circumference of about 31. 4 meters. Find the area of the wallway
Answers
The area of the walkway is 24π square meters.
To find the area of the walkway, we need to subtract the area of the inner circle from the area of the outer circle.
The inner circle has a radius of 5 meters, so its area can be calculated using the formula for the area of a circle: A_inner = π * \((r_inner)^{2}\).
A_inner = π * \(5^{2}\) = 25π square meters.
The outer circle has a radius equal to the sum of the inner radius and the width of the walkway. In this case, the outer radius is 5 + 2 = 7 meters.
The area of the outer circle can be calculated in the same way: A_outer = π * \((r_outer)^{2}\).
A_outer = π * \(7^{2}\) = 49π square meters.
Now, we can find the area of the walkway by subtracting the area of the inner circle from the area of the outer circle: A_walkway = A_outer - A_inner.
A_walkway = 49π - 25π = 24π square meters.
The area of the walkway is 24π square meters, where π (pi) is a mathematical constant approximately equal to 3.14159.
To learn more about area here:
https://brainly.com/question/32312055
#SPJ4
Help please due today

Answers
Answer:
Line a. goes to table 3, line b. goes to table 2, and line c. goes to table 1.
Step-by-step explanation:
Here are the 3 lines graphed (I even labeled each for you) so you can have a bit of a visual.
Hopefully you can find the points on each graph.
(Hint: The x row represents the x coordinate of an ordered pair, and the y row represents the y coordinate of an ordered pair.)
Ordered pairs look like this btw (x,y)
Hope this helps :)


Dan painted a wall of 25m by 20m and the money he got for his work was Rs. 20 per square
meter. How much money he made? He always gives half of his income to orphanage.
Calculate how much money he gave to the orphanage? What value you learn from Dan?
Answers
Answer:
He made Rs.500
He gave Rs.250 to the orphanage
Sharing
Which statement will prove that PQS is similar to JKL?
Answers
Answer:
Q=L
Step-by-step explanation:
Answer:A
Step-by-step explanation:
Given sin A=-√3/2 and tan A >0, find cos A.
PLEASE HURRY AND SHOW WORK
Answers
Answer:
Below in bold.
Step-by-step explanation:
We have a right triangle here with the hypotenuse = 2 and the legs are 1 and √3.
If tan A > 0 then the opposite side to < A in the triangle is greater than the adjacent so the leg opposite angle A is √3 and the adjacent side = 1.
So cos A = adj/hyp = 1/2.
3². (2²+4)
What is the value of the expression
22
?
A. 10
B. 15
C. 19
D. 27
someone please help lol
Answers
Hope this helps :)
Could I also have brainliest
What is the inverse of
\(f(x) = \sqrt{x} + 6\)
for
\(x \geqslant 0\)
?
A:
\(f(x) = (x - 6) {}^{2} \)
B:
\(f(x) = x {}^{2} - 6\)
C:
\(f(x) = x {}^{2} + 6\)
D:
\(f(x) = \sqrt{x + 6} \)
Answers
Step by step exploration