at the valentines day dance the sponsors handed out candy kisses to each person entering the dance. one group received a total of 20 candy kisses as they entered. another group of dancers received a total of 52 candy kisses. each person received the same amount of candy. what was the greatest possible number of candy kisses each person could have received
Answers
the maximum number of candy kisses that each person could have received is 4.
What was the greatest possible number of candy kisses each person could have received?We know that each person receives the same number of candy.
Now, one group of K people receives 20 candy.Another group of N people receives 52 candy.Then the quotients between the number of candy and the number of people should give the same value:
20/K = 52/N
Let's find the common factors between 20 and 52, to do so, we need to rewrite the two numbers as a product of prime factors:
20 = 2*10 = 2*2*5
52 = 2*26 = 2*2*13
The greatest common factor between 20 and 52 is (2*2) = 4
Then, if each person receives 4 candy:
The group that receives 20 candy:
20/K = 4
20/4 = k = 5
That group has 5 people.
The group that receives 52 candy:
52/N = 4
52/4 = N = 13
This group has 13 people.
Then the maximum number of candy kisses that each person could have received is 4.
If you want to learn more about the greatest common factors:
https://brainly.com/question/219464
#SPJ1
Related Questions
Michael plans to make contributions to his retirement account for 12 years. After the last contribution, he will start withdrawing $10,000 a quarter for 10 years. Assuming Mike's account earns 8% compounded quarterly, how large must his quarterly contributions be during the first 12 years, in order to accomplish his goal?
Answers
Michael must contribute $7,849.55 quarterly during the first 12 years in order to achieve his retirement goals.
Why is the time value of money significant in finance? What does it mean?The idea that money now is worth more than the same amount of money in the future owing to the potential earning capacity of money over time is known as the time value of money, and it is a basic concept in finance. The notion behind the concept is that money may be invested to produce interest or other returns, and that over time, inflation and other variables affect how much money is worth.
Given that, the contributions are made for 12 years.
The future value is thus given by:
\(FV = P[((1+r)^n - 1)/r]\)
The number of periods are:
12*4 = 48 periods.
The interest rate per quarter is 8%/4 = 2%.
Substituting the values we have:
\(FV = P[((1+r)^n - 1)/r] \\\\=P[((1+0.02)^48 - 1)/0.02] \\\\= P[67.242]\)
Now, for present value of an annuity, we get:
\(PV = C[(1-(1+r)^-n)/r] \\\\= 10000[(1-(1+0.02)^-40)/0.02] \\\\=528,113.20\)
Setting the two values equal we have:
P[67.242] = 528,113.20
P = 7,849.55
Hence, Michael must contribute $7,849.55 quarterly during the first 12 years in order to achieve his retirement goals.
Learn more about future value here:
https://brainly.com/question/28952696
#SPJ1
Of the 14 clients at Bob's salon, 7 of them have red hair. What is the probability that a randomly selected client at Bob's salon has red hair? P(red) =
Answers
Now
\(\\ \rm\Rrightarrow P(E)=\dfrac{|E|}{|S|}\)
\(\\ \rm\Rrightarrow P(E)=\dfrac{7}{14}=1/2\)
Answer:
\(\mathsf{Probability \ of \ an \ event \ occurring = \dfrac{Number \ of \ ways \ it \ can \ occur}{Total \ number \ of \ outcomes}}\)
Given:
Total number of outcomes = total number of clients = 14Number of ways it can occur = number of clients with red hair = 7\(\implies \mathsf{Probability \ of \ red\ hair= \dfrac{7}{14}=\dfrac12=0.5}\)
Given the table below, what is the x-intercept of the linear function?

Answers
Answer:
-6
Step-by-step explanation:
J is the midpoint of CT
J
T
If:
CJ = 2x – 1 and
JT = 82 – 43
Find CT.
Answers
Answer:
78
Step-by-step explanation:
JT = half the distance so JT x 2 = CT
JT = 39
39 x 2 = 78
A single card is drawn from a deck of 52 cards. What are the odds in favor of drawing a 7?
Answers
The odds in favor of drawing a 7 are 1 to 12.
What is probability?
Probability is a measure of the likelihood or chance of an event occurring. It is expressed as a number between 0 and 1, where 0 represents an impossible event and 1 represents a certain event.
There are four 7s in a deck of 52 cards, so the probability of drawing a 7 is 4/52, which simplifies to 1/13. The odds in favor of drawing a 7 are the ratio of the probability of drawing a 7 to the probability of not drawing a 7, which is:
(1/13) : (12/13
We can simplify this ratio by dividing both terms by the greatest common factor, which is 1:
(1/13) : (12/13) = 1 : 12
Therefore, the odds in favor of drawing a 7 are 1 to 12.
To know more about probability visit :
https://brainly.com/question/13604758
#SPJ1
solve this system of equations by using the elimination method x-5y=16 4x-2y=-8
Answers
Answer:
(- 4, - 4 )
Step-by-step explanation:
x - 5y = 16 → (1)
4x - 2y = - 8 → (2)
multiplying (1) by - 4 and adding to (2) will eliminate x
- 4x + 20y = - 64 → (3)
add (2) and (3) term by term to eliminate x
(4x - 4x) + (- 2y + 20y) = - 8 - 64
0 + 18y = - 72
18y = - 72 ( divide both sides by 18 )
y = - 4
substitute y = - 4 into either of the 2 equations and solve for x
substituting into (1)
x - 5(- 4) = 16
x + 20 = 16 ( subtract 20 from both sides )
x = - 4
solution is (- 4, - 4 )
Find the circumference of each circle.
7) diameter = 22 km

Answers
Step-by-step explanation:
Diameter (d) = 22 km
circumference(c)
= π d
= 3.14 * 22
= 69.02 km
Hope it will help :)
3x - 5 < 19
Show work
Answers
We can solve the inequality by isolating the variable, we will get:
x < 8
How to solve the inequality?
This is just like an equation, what we need to do is isolate the variable in one of the sides.
Here we have the inequality:
3x - 5 < 19
To solve it, let's isolate the variable x.
We can start by adding 5 in both sides, then we will get:
3x < 19 + 5
3x < 24
Now let's divide both sides by 3, so we will get:
x < 24/3
x < 8
Laern more about inequalities at:
https://brainly.com/question/24372553
#SPJ1
x,2x+1,11 are three consecutive terms of arithmetic sequence..find X and term5
Answers
An arithmetic progression is a set of numbers with a fixed difference between any two succeeding numbers (A.P.). Examples of A.P. include 3, 6, 9, 12, 15, 18, and 21.
What in math are AP and GP?A.P. and G.P. application: A series of terms known as an arithmetic progression (AP) have identical differences. In a geometric progression (GP), the common ratio is multiplied by the previous term to produce each succeeding term.
Given,
a₁ = x
a₂ = 2x + 1
a₃ = 11
a₂ - a₁ = a₃- a₂
(2x + 1) - (x) = 11 - (2x + 1)
2x - x + 1 = 11 - 2x - 1
x + 1 = -2x + 10
2x + x = 10 - 1
3x/3 = 9/3
x = 3
The arithmetic sequence: 3, 7, 11
Common difference: 4
To know more about arithmetic progression visit:-
brainly.com/question/29259404
#SPJ1
You are installing a rectangular pool in your backyard. The pool measures 24 feet by 16 feet. You also would like to build a concrete walkway around the pool. You have allocated 560 ft? of your backyard for both the pool and the walkway around it. How wide should you make the walkway?
Answers
Answer:
The walkway should be 2ft wide.
Step-by-step explanation:
Let x be the width of the walkway surrounding the pool.
The area including the pool is 560ft².
Let's solve for the value of x.
The length plus twice the width of the pool is multiplied by the width plus twice the width of the pool. This makes up the whole area.
A = lw
560 = (24 + 2x)(16 + 2x)
560 = 384 + 48x + 32x + 4x²
4x² + 80x + 384 - 560 = 0
4x² + 80x - 176 = 0
Divide the whole equation by 4
x² + 20x - 44 = 0
(x + 22)(x -2) = 0
x = -22; x = 2
Since we are dealing with dimensions, take the one with the positive value.
x = 2ft
Let's check
560ft² = (24ft + 2x)(16ft + 2x)
560ft² = (24ft + 2(2ft)) (16ft + 2(2ft))
560ft² = (24ft + 4ft)(16ft + 4ft)
560ft² = (28ft)(20ft)
560ft² = 560ft² ✔

Work out the perimeter of the shaded shape on the centimetre grid.
Give the answer in cm and no spam.

Answers
Answer:
The perimeter of this rectangle is 10 cm.
A museum has 382 butterflies it wants to put in display
cases. Each case can hold 8 butterflies. How many
cases does the museum need?
Answers
Answer:D: 48
Step-by-step explanation:
In an election, suppose that 40% of voters support a new tax on fast food. If we poll 165 of these voters at
random, the probability distribution for the proportion of the polled voters that support a new tax on fast food
can be modeled by the normal distibution pictured below. Complete the boxes accurate to two decimal
places.

Answers
The values accurate to two decimal places for -2 standard deviation, mean, and +2 standard deviation are 0.30, 0.40, and 0.49, respectively.
What are the values of the mean and the standard deviation?We can use the following formulas to calculate the mean and standard deviation of the sampling distribution:
Mean: μ = p = 0.40 (since the population proportion is 0.40)
Standard deviation: σ = √((p(1-p))/n)
σ = √((0.40(1-0.40))/165)
σ = 0.049
Now we can calculate the values for -2SD, mean, and +2SD as follows:
-2SD: μ - 2σ = 0.40 - 2(0.049) = 0.30
Mean: μ = 0.40
+2SD: μ + 2σ = 0.40 + 2(0.049) = 0.49
Learn more about standard deviation at: https://brainly.com/question/24298037
#SPJ1
What is the distance of (2,7) and (-5,5
Answers
Answer:
7.28 units
Step-by-step explanation:
To find the distance between two points, we use the distance formula:
d = √((x2 - x1)^2 + (y2 - y1)^2)
Using the coordinates given, we can plug in the values:
d = √((-5 - 2)^2 + (5 - 7)^2)
d = √((-7)^2 + (-2)^2)
d = √(49 + 4)
d = √53
Therefore, the distance between (2,7) and (-5,5) is approximately 7.28 units (rounded to two decimal places).
Consider the relationship chart for the a fast-food restaurant,
Assume that the areas required for each department are:
Department Area Required (Square feet)
(CB) 300
(CF) 200
(PS) 200
(DD) 200
(CS) 300
Assume facility dimension of 6 (horizontal) by 8 (vertical) squares, where each square is 5 feet on a side. As a result, for example the CB department requires 12 squares. Develop a layout for the fast-food restaurant.
Answers
The layout of the fast-food restaurant of dimensions 6 by 8 5 feet squares is presented in the attached table created with Sheets.
How can the required layout be found?The dimensions of the facility are;
Horizontal = 6 squares
Vertical = 8 squares
The side length of each square = 5 feet
Therefore;
Area of each square = 5² ft.² = 25 ft.²
Number of squares, n, required by each dependent are therefore;
CB department, n = 300 ÷ 25 = 12 squares
CF department, n = 200 ÷ 25 = 8 squares
PS department, n = 8 squares
DD department, n = 8 squares
CS department, n = 12 squares
A layout for the fast-food restaurant is therefore;
The first three vertical columns of 8 squares each are occupied by the CF, PS, and DD departments. The remaining 3 by 8 squares are occupied by the CB department, (3 by 4 squares), and the CS department, (3 by 4 squares)Please see the attached table layout created using Sheets.
Learn more about finding the area of regular figures here:
https://brainly.com/question/316492
#SPJ1
Need help with this question ! Due soon*

Answers
Answer:
x = 10, AB = 57
Step-by-step explanation:
In a trapezoid, the length of the median is one-half the sum of the lengths of the bases. From this, we have:
\( \frac{1}{2} (5x + 7 + 8x - 11) = 63\)
\(13x - 4 = 126\)
\(13x = 130\)
\(x = 10\)
\(5(10) + 7 = 50 + 7 = 57\)
What is 3 3/4 ft to yards as a mixed number?
Answers
The value of 3¾ft in yards would be = 1 6/25 yard
What is a mixed number?A mixed number is the type of number that is made up of three parts such as the whole number, a numerator and a denominator.
To convert to yards;
1 ft = 0.33 yard
3¾ = X yards
make x yards the subject of formula;
X yards = 3¾ × 0.33
X yards = 3.75×0.33
X yards = 1.24 yards
X yards in mixed number= 124/100 = 31/25 = 1 6/25 yard.
Note that the final value which is 124/100 is reduce to the lower figure by dividing through with 4 to arrive at the mixed number 1⁶/25
Learn more about mixed numbers here:
https://brainly.com/question/21610929
#SPJ1
on a piece of paper, graph:

Answers
Answer:
every public company is listed company true or false every public company is listed company true or false every public company is listed company true or false every public company is listed company true or false every public company is listed company true or false every public company is listed company true or false every public company is listed company true or false
HELP MEEEEEEEEEEEE WILL GIBE BRAINLISTTTTTTT

Answers
Answer:
b
Step-by-step explanation:
Answer:
The answer is C, 2/9
Step-by-step explanation:
Since there 18 marbles in total and 4 blue marbles, that makes the probability 4/18. Although, 4/18 has to be simplified, which is 2/9
Which of the following shows numbers ordered from least to greatest

Answers
Answer:
A
Step-by-step explanation:
It is option A: -2, -1, 0, 1
Susan was supposed to use 5/4 of a cup of butter
in her recipe, but she only used 3/4 of a cup of butter.
a. What fraction of the butter that she should
have used did Susan actually use? Make a
math drawing to help you solve this problem
and explain your solution.
b. Describe the different unit amounts that occur
in part (a). Discuss how one amount can be de-
scribed with two different fractions depending
on what the unit amount is taken to be.
Answers
Answer:
\(a.\ \dfrac{3}{5}\)
Step-by-step explanation:
We can see the fractions \(\frac{5}{4}\) and \(\frac{3}{4}\) of cups.
It can be seen that denominator has 4 i.e. the fraction \(\frac{1}{4}\).
Let us suppose, a unit is equal to \(\frac{1}4\) of a cup.
Susan was supposed to use \(\frac{5}{4}\) of a cup.
i.e. 5 units of butter was to be used.
But, actual recipe has only 3 units of butter.
\(\text{Fraction of butter used} = \dfrac{\text{Units of butter used}}{\text{Unit of butter Susan was supposed to use}}\)
a. \(\text{Fraction of butter used} = \dfrac{3}{5}\)
Alternatively, we could have directly divided the given fractions:
\(\dfrac{\dfrac{3}{4}}{\dfrac{5}{4}} = \dfrac{3}{5}\)
The fraction of the butter that she should have used did Susan actually use is :
Fractions =5/4 and 3/4 of cups.
Denominator = 4 i.e. the fraction 1/4
Let us suppose,
A unit is equal to 1/4 of a cup.
Susan was supposed to use 5/4 of a cup.
5 units of butter was to be used.
But, actual recipe has only 3 units of butter.
Fraction of butter used=unit of butter used/unit of butter
that was supposed to
be use
=3/4/5/4
=3/5
The fraction of the butter that she should have been used is 3/5.
Find out more information about "Fractions":
https://brainly.com/question/9047718referrer=searchResults
Whitney was visiting Big Bend Ranch
State Park. At the entrance, she saw a
map of the park. The legend stated
that 1.5 inches on the map represents
20 feet in the park. On the map, how
many inches would represent 60
actual feet?
Answers
Answer:
4.5 inches on the map would represent 60 actual feet.
Step-by-step explanation:
Given that:
1.5 inches on map represents 20 feet in the park.
x be the inches on map that represents 60 feet in the park.
Ratio of distance on map to actual distance :: Ratio of distance on map to actual distance
1.5 : 20 :: x : 60
Product of mean = Product of extreme
20*x = 1.5*60
20x = 90
Dividing both sides by 20
\(\frac{20x}{20}=\frac{90}{20}\\x=4.5\)
Hence,
4.5 inches on the map would represent 60 actual feet.
In ADEF, f= 33 inches, ZF=140° and ZD=5°. Find the length of e, to the nearest 10th
of an inch.
Answers
The length of e is 29.53 inches.
what is Sine Law?In the following, the law of sine is presented in detail: In a triangle, the sine of angle A divided by side "a" equals the sine of angle B divided by side "b" equals the sine of angle C divided by side "c".
Given:
f= 33 inches
<F= 140, <D = 5
Now,
<E= 180 - (<F+ <D) = 180 - (140 + 5) = 35
Using Sine law
sin F / f = sin E/ e
sin 140 / 33 = sin 35 / e
0.642/ 33 = 0.573 / e
0.0194 e= 0.573
e= 29.53 inches
Hence, the length of e is 29.53 inches.
Learn more about sine law here:
https://brainly.com/question/17289163
#SPJ1
Please help me I was sick today and missed out on class and I don’t understand this question

Answers
I hope this is clear enough , although I did not arrive at the same answer using x in both equation .


This shows two functions.
f(x)=5x-7
g(x)=x+4
which function represents
h(x) = f(x) ⋅ g(x)

Answers
Answer:
its c just so u know
Step-by-step explanation:
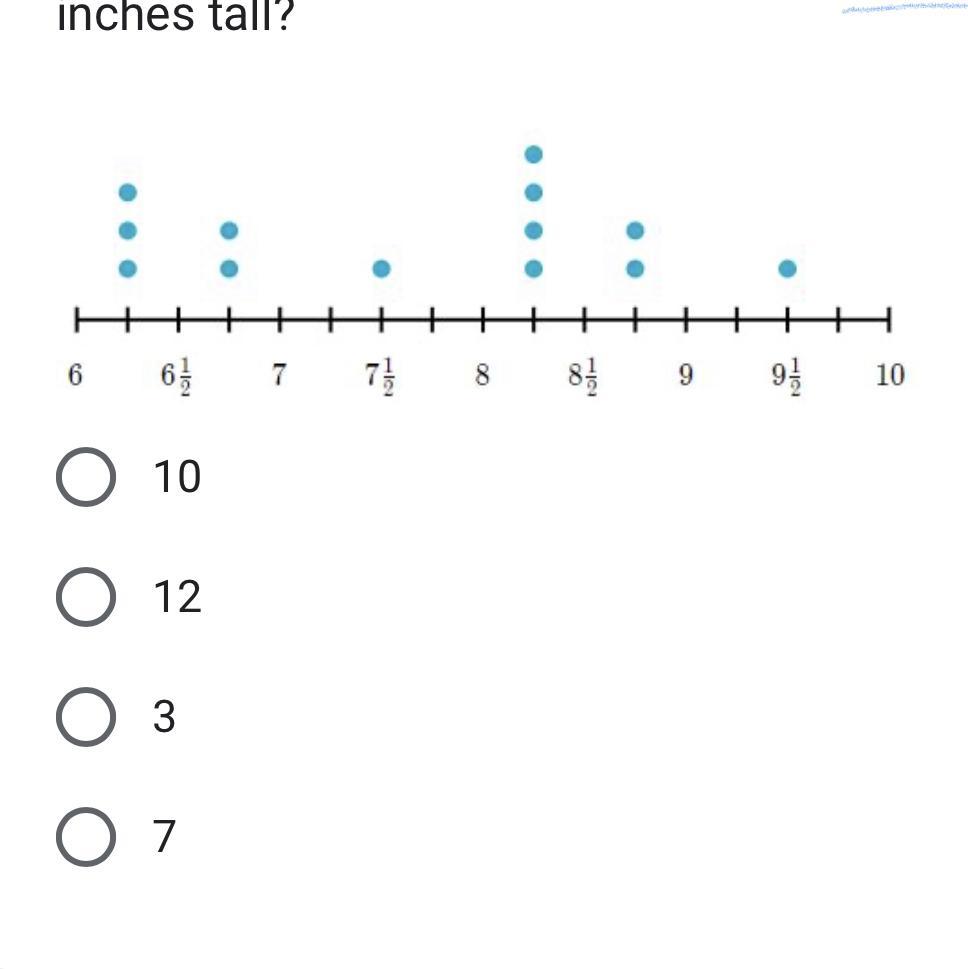
4) Students in Ms. Udon
science class planted 13
conifers in different places
around the school yard. They
measured the heights (in inches)
of the conifers one month after
planting them. How many
conifers are greater than 6 1/4
inches tall but less than 8 1/2
inches tall?
Answers
Considering the dot plot, the tallest conifer is 3.25 inches taller than the shortest conifer.
This shows, with dots, the number of times that each of the measures appears in a data set.
For finding the dot plot, we have that:
The shortest conifer measures 6 and 1/4
= 6.25 inches.
The tallest conifer measures 9.5 inches.
The difference is:
9.5 - 6.25 = 3.25 inches.
Therefore the tallest conifer is 3.25 inches taller than the shortest conifer.
More can be learned about a dot plot at;
brainly.com/question/24912483
#SPJ1
One centimeter on the map represents 10 meters on the ground?
Answers
parallel and perpendicular lines
Answers
Answer:
Parallel lines are lines in a plane that are always the same distance apart. Parallel lines never intersect. Perpendicular lines are lines that intersect at a right (90 degrees) angle.
Step-by-step explanation:
A plane flying with a constant speed of 360 km/h passes over a ground radar station at an altitude of 1 km and climbs at an angle of 30°. At what rate (in km/h) is the distance from the plane to the radar station increasing a minute later? (Round your answer to the nearest whole number.)
Answers
The rate (in km/h) at which the distance from the plane to the radar station is increasing a minute later is 0 km/h (rounded to the nearest whole number).
To solve this problem, we can use the concepts of trigonometry and related rates.
Let's denote the distance from the plane to the radar station as D(t), where t represents time. We want to find the rate at which D is changing with respect to time (dD/dt) one minute later.
Given:
The plane is flying with a constant speed of 360 km/h.
The plane passes over the radar station at an altitude of 1 km.
The plane is climbing at an angle of 30°.
We can visualize the situation as a right triangle, with the ground radar station at one vertex, the plane at another vertex, and the distance between them (D) as the hypotenuse. The altitude of the plane forms a vertical side, and the horizontal distance between the plane and the radar station forms the other side.
We can use the trigonometric relationship of sine to relate the altitude, angle, and hypotenuse:
sin(30°) = 1/D.
To find dD/dt, we can differentiate both sides of this equation with respect to time:
cos(30°) * d(30°)/dt = -1/D^2 * dD/dt.
Since the plane is flying with a constant speed, the rate of change of the angle (d(30°)/dt) is zero. Thus, the equation simplifies to:
cos(30°) * 0 = -1/D^2 * dD/dt.
We can substitute the known values:
cos(30°) = √3/2,
D = 1 km.
Therefore, we have:
√3/2 * 0 = -1/(1^2) * dD/dt.
Simplifying further:
0 = -1 * dD/dt.
This implies that the rate at which the distance from the plane to the radar station is changing is zero. In other words, the distance remains constant.
for such more question on distance
https://brainly.com/question/7243416
#SPJ8
Find the perioa
equation.
llowing
y = 2 cos(5x + 3) - 6
77
Period = [2]T
Give your answer in simplest form.
![Find the perioaequation.llowingy = 2 cos(5x + 3) - 677Period = [2]TGive your answer in simplest form.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/LQPTncYwbgWAlBk9oUI1EamQ5J0oFRZg.png)
Answers
Answer:
In the equation y = 2 cos(5x + 3) - 6, we can ignore the coefficients 2 and -6 for the purposes of calculating the period because they do not change the period. They only change the amplitude (2) and vertical shift (-6) of the function.
The coefficient 5 in front of x inside the cosine function affects the period of the function. It is a horizontal compression/stretch of the graph of the function.
The period of the basic cosine function, y = cos(x), is 2π. When there is a coefficient (let's call it b) in front of x, such as y = cos(bx), the period becomes 2π/b.
So, in your case, b = 5, so the period T of the function y = 2 cos(5x + 3) - 6 is:
T = 2π / 5
This is the simplest form for the period of the given function.