Billy has a $40 gift card. She spends $10 per week. Write a linear equation for this situation.
(Hint: Use y = mx + b, where y is money remaining, m is loss per week, and b is the starting money.)
Answers
She has $40 to begin with and spends $10 per week.
Related Questions
The graph of $y = f(x)$ is symmetric across the line $x = 5$. The graph also passes through the point $(8,-7).$ Find another point that must lie on the graph of $y = f(x).$
Answers
Because we know one point and an axis of symmetry, we know that the point (2, -7) must lie on the graph.
Which other point must lie on the graph?If a function has a line of symmetry at x = x₀, then we know that:
f(x₀ + x) = f(x₀ - x).
So we have symmetry around that line.
Then, if the line of symmetry is at x = 5 and we know that:
f(8) = f(5 + 3) = -7
We also must have:
f(2) = f(5 - 3) = -7
Then the point (2, - 7) must be on the graph.
If you want to learn more about symmetry you can read:
https://brainly.com/question/11408596
find the surface area of a square based pyramid with a side length of 5cm and a slant height of 5cm
Answers
Answer:
Step-by-step explanation:
The surface area of a square pyramid = 1/2 * slant height * base perimeter + area of base
The slant height is 5 cm
The base perimeter is 4 * 5 cm = 20 cm
The area of the base is 5 cm * 5 cm = 25 cm**2
Plugging into the formula the area =
1/2 * 5 cm * 20 cm + 25 cm**2 =
5 cm * 10 cm + 25 cm**2 =
50 cm**2 + 25 cm**2 = 75 cm**2
Solve each multiple choice question by showing your work step by step
1. Which expression is equivalent to (-18) - 16n?
Answers
Answer:
-2(9+8n)
Step-by-step explanation:
open the bracket
-18-16n
factorize by -2
-2(9+8n)
The product of a number and negative three is no more than 10
Answers
Answer:
The answer is ≤-3.3
Step-by-step explanation:
If you multiply -3.3 x -2 it will give you 9.99 anything above that would go past 10.
So the answer is less than or equal to -3.3 because this number or anything below it on a number line multiplied by -3 will never go past 10.
Hope this helps!
The perimeter of a rectangular lawn i 50 meter. It' 16 meter long how wide i it?
Answers
The width of the rectangle is 9 meter.
Now, According to the question:
The perimeter of a rectangle is defined as the sum of all the sides of a rectangle. For any polygon, the perimeter formulas are the total distance around its sides. In case of a rectangle, the opposite sides of a rectangle are equal and so, the perimeter will be twice the width of the rectangle plus twice the length of the rectangle and it is denoted by the alphabet “p”.
Now, Solving the problem:
Perimeter of rectangle is 50 meter sq.
Length of the rectangle(L) is 16 meter.
We have to find the width (W) of the rectangle.
We know that,
Perimeter of rectangle is = 2 (L + W)
50 = 2(16 + W)
50 = 32 + 2W
2W = 50 - 32
2W = 18
W = 18/2
W = 9
Hence, The width of the rectangle is 9 meter.
Learn more about Perimeter of rectangle at:
https://brainly.com/question/22109593
#SPJ4
Using complete sentences, describe the error in the steps used to solve the equation. There will be no problems that don’t have an error.
“The error was made when.....”

Answers
Are any of the measures of dispersion among the range, the variance, and the standard deviation, resistant? explain.
Answers
Answer:
There isn't much to say because there is no image with the options but, no, all these measures of desperation are affected by extreme values
-) Write the prime factorization of 968.
A) 2-2 11 11 11
B) 2.2.2.2.11
C) 2.2.2.11-11
D) 8-121
Answers
Answer:
2,2,2,11,11
Step-by-step explanation:
968/2
484/2
242/2
121/11
11/11
A is directly proportional to the square root of B
When A = 50, B+4 . Find A in terms of B
Answers
Answer:
A=50, B=4
A is directly proportional to the square root of B
name the constant 'k'
A = k*B^0.5
50 = k*4^0.5
50=2k
k=25
=> A =25 root B
i.e, A = 25*B^0.5 (The answer should be written the way it is written in the attached picture)

A written in terms of B is 25√B.
What is direct and inverse proportion ?In direct proportion if one quantity increases the other quantity also increases and vice versa.In case of inverse proportion when one quantity increases the other quantity decreases and vice versa.
According to the given question A is directly proportional to the square root of B.
∴ A = K\(\sqrt{B}\)
Given when A = 50 B = 4.
50 = K\(\sqrt{4}\)
50 = 2k
k = 25.
So, A =25√B.
learn more about proportion here :
https://brainly.com/question/7096655
#SPJ2
Type the correct answer in the box. Use numerals instead of words. If necessary, use/ for the fraction bar.
Given the figure, find the total area of the shaded region.
D
8-
6-
4-
2-
O
-2-
o
S
The area of the shaded region is
B
R
8
с
square units
Answers
The value of the total area of the shaded region are,
⇒ 42 units²
We have to given that;
Sides of rectangle are,
AB = 9
BC = 6
Hence, The area of rectangle is,
⇒ 9 x 6
⇒ 54 units²
And, Area of triangle is,
A = 1/2 × 4 × 6
A = 12 units²
Thus, The value of the total area of the shaded region are,
⇒ 54 - 12
⇒ 42 units²
So, The value of the total area of the shaded region are,
⇒ 42 units²
Learn more about the rectangle visit:
https://brainly.com/question/2607596
#SPJ1

The radius of a circle is 18 kilometers. What is the circle's area?
Answers
Answer: 1017.36 km²
Step-by-step explanation:
Area of Circle = πr² = 3.14×18×18 = 1017.36 km²
if f(x) =4x^3+3x-2 then what is the remainder when f(x) is divided by x-4
Answers
Answer:
x-4= 0
X= 4
from the function above
f(x) =4x^3+3x-2
4(4)^3 + 3(4) - 2
256+12- 2
==> 266
Answer:
Hiya There!!
_________________
4×⅛ = ½
_________________
“I think it’s a mistake to ever look for hope outside of one’s self.”
– Arthur Miller
Think of life as a mytery because well it sort of is! You don't know what may happen may be good or bad but be a little curious and get ready for whatever comes your way!! ~Ashlynn
What is the area of this figure?
3 ft
6 ft
8 ft
17 ft
14 ft
16 ft
Pls help me its due today and I need a score of 80 and I got a 44 pls help

Answers
Answer:
38
Step-by-step explanation:
This might be wrong, But to my calculations it is
in a circle, a sector with central angle is 225 degrees intercepts an arc of length 30pi in. find the diameter of the circle
Answers
The diameter of the circle is approximately 60 inches.
To explain further, we can use the formula relating the central angle of a sector to the length of its intercepted arc. The formula states that the length of the intercepted arc (A) is equal to the radius (r) multiplied by the central angle (θ) in radians.
In this case, we are given the central angle (225 degrees) and the length of the intercepted arc (30π inches).
To find the diameter (d) of the circle, we need to find the radius (r) first. Since the length of the intercepted arc is equal to the radius multiplied by the central angle, we can set up the equation 30π = r * (225π/180). Simplifying this equation gives us r = 20 inches.
The diameter of the circle is twice the radius, so the diameter is equal to 2 * 20 inches, which is 40 inches. Therefore, the diameter of the circle is approximately 60 inches.
In summary, by using the formula for the relationship between central angle and intercepted arc length, we can determine the radius of the circle. Doubling the radius gives us the diameter, which is approximately 60 inches.
for such more questions on diameter
https://brainly.com/question/30460318
#SPJ8
In volleyball there are two different scoring systems in which a team must win by at least two points. In both systems, a rally begins with a serve by one of the teams and ends when the ball goes out of play or touches the floor or a player commits a fault. The team that wins the rally gets to serve for the next rally. Games are played to 15, 25 or 30 points. a) In rally point scoring, the team that wins a rally is awarded a point no matter which team served for the rally. Assume that team A has probability p of winning a rally for which it serves, and that team B has probability q of winning a rally for which it serves. We can model the end of a volleyball game starting from a tied score using a Markov chain with the following six states: 1 tied - A serving 2 tied - B serving 3 A ahead by 1 point - A serving 4 B ahead by 1 point - B serving 5 A wins the game 6 B wins the game Find the transition matrix for this Markov chain. b) Suppose that team A and team B are tied 15-15 in a 15-point game and team B is serving. Let p = q = 0.65. Find the probability that the game will not be finished after three rallies.
Answers
a) The transition matrix for the Markov chain representing the end of a volleyball game can be constructed based on the given states. The matrix will have dimensions 6x6, with each element representing the probability of transitioning from one state to another. The transition probabilities depend on the probabilities of winning rallies for each team. The resulting transition matrix is as follows:
[ 0 0 0 0 1 0 ] [ 0 0 0 0 0 1 ] [ p 0 0 0 0 1-p ] [ 0 q 0 0 1-q 0 ] [ 0 0 0 0 1 0 ] [ 0 0 0 0 0 1 ]
In this matrix, each row represents a current state, and each column represents a possible next state. The element in the i-th row and j-th column represents the probability of transitioning from state i to state j.
b) To find the probability that the game will not be finished after three rallies when team B is serving and both teams are tied 15-15, we need to calculate the probability of being in the states "tied - B serving" after three rallies. Using the given transition matrix and probabilities p = q = 0.65, we can perform matrix multiplication to obtain the state probabilities after three transitions.
Starting with an initial state vector [0 0 0 1 0 0], representing being in the state "tied - B serving," we multiply it by the transition matrix three times to find the state probabilities after three rallies. The probability of the game not being finished is the sum of the probabilities in the states "tied - B serving," "A ahead by 1 point - A serving," and "B ahead by 1 point - B serving."
Performing the calculations, the probability that the game will not be finished after three rallies is approximately 0.1721 or 17.21%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
The transition matrix for the Markov chain representing the end of a volleyball game, considering rally point scoring, can be derived based on the six states described: 1) tied - A serving, 2) tied - B serving, 3) A ahead by 1 point - A serving, 4) B ahead by 1 point - B serving, 5) A wins the game, and 6) B wins the game.
.
(a) To construct the transition matrix for the Markov chain, we consider the possible transitions between the six states. The matrix will have dimensions 6x6, with each element representing the probability of transitioning from one state to another. For example, the probability of transitioning from state 1 (tied - A serving) to state 2 (tied - B serving) can be calculated based on the probabilities p and q mentioned in the problem statement. By considering all possible transitions, the complete transition matrix can be obtained.
(b) In this scenario, we start with state 2 (tied - B serving) and need to find the probability that the game will not be finished after three rallies. To calculate this probability, we can use the transition matrix obtained in part (a) and perform matrix multiplication. By multiplying the initial state vector (corresponding to state 2) with the transition matrix three times, we can find the probabilities of ending up in each state after three rallies. The probability of the game not being finished after three rallies would be the sum of the probabilities in states 1 and 2, which represent tied scores.
to learn more about Markov chain click here
brainly.com/question/30465344
#SPJ11
Determine the equation of the circle with center (-1,-2)(−1,−2) containing the point (0,6)
Answers
The equation of the circle with center (−1,−2) containing the point (0,6).
(x + 1)^2 + (y + 2)^2 = 65
How to determine the equation of the circle?
Remember that the equation of a circle with radius R and center (a, b) is written as:
(x - a)^2 + (y - b)^2 = R^2
Here we know that the center of the circle is (-1, -2), then our equation is something like:
(x + 1)^2 + (y + 2)^2 = R^2
We know that our circle contains the point (0, 6), replacing these values in the equation above we get:
(0 + 1)^2 + (6 + 2)^2 = R^2
1 + 8^2 = R^2
65 = R^2
Then the circle equation is:
(x + 1)^2 + (y + 2)^2 = 65
Learn more about circle equations:
https://brainly.com/question/1559324
#SPJ1
sketch the vector field f by drawing a diagram like this figure. f(x, y) = yi − xj x2 + y2
Answers
The length vector is 1. So the sketch vector field f is given below. So the option a is correct.
In the given question, the vector field F by drawing a diagram like this figure.
The given vector field F is:
F(x, y) = (yi + xj)/√(x^2 + y^2)
We can write the vector field as:
F(x, y) = yi/√(x^2 + y^2) + xj/√(x^2 + y^2)
Here
F(x, y) = [y/√(x^2 + y^2)]^2 + [x/√(x^2 + y^2)]^2
F(x, y) = y^2/(x^2 + y^2) + x^2/(x^2 + y^2)
F(x, y) = (y^2+ x^2)/(x^2 + y^2)
F(x, y) = 1
F(0, y) = y/|y| = ±1
F(x, 0) = x/|x| = ±1
So the length vector is 1.
So the sketch vector field f is given below:
To learn more about vector field link is here
brainly.com/question/24332269
#SPJ4
The complete question is:
Sketch the vector field F by drawing a diagram like this figure.
F(x, y) = (yi + xj)/√(x^2 + y^2)


Solve by the substitution method.
6x + 8y = 0
-7x + y = 31
Answers
Answer:
(-4, 3)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Algebra I
Solving systems of equations using substitution/eliminationStep-by-step explanation:
Step 1: Define Systems
6x + 8y = 0
-7x + y = 31
Step 2: Rewrite Systems
-7x + y = 31
Add 7x to both sides: y = 7x + 31Step 3: Redefine Systems
6x + 8y = 0
y = 7x + 31
Step 4: Solve for x
Substitution
Substitute in y: 6x + 8(7x + 31) = 0Distribute 8: 6x + 56x + 248 = 0Combine like terms: 62x + 248 = 0Isolate x term: 62x = -248Isolate x: x = -4Step 4: Solve for y
Define equation: -7x + y = 31Substitute in x: -7(-4) + y = 31Multiply: 28 + y = 31Isolate y: y = 3A firm uses two inputs x and y, and their profit function is P(x,y)=2xy-3x+y. Input x costs $2 each and y costs $3 each and they are constrained to spend a total of $100 on inputs. If the firm wants to maximise profit, they should use of input x, of input y. In addition, the shadow price will be Round your answer to two decimal places.
Answers
The optimal allocation is x = -1/2, y = 3/2, with a shadow price of 1.50.
What is Supply and demand equilibrium factors?To maximize profit, the firm needs to determine the optimal allocation of inputs x and y within the budget constraint of $100.
Let's assume the firm uses 'a' units of input x and 'b' units of input y. Since each unit of x costs $2 and each unit of y costs $3, the total cost constraint can be expressed as:
2a + 3b ≤ 100
To maximize profit, we need to differentiate the profit function P(x, y) with respect to both inputs and set the derivatives equal to zero:
∂P/∂x = 2y - 3 = 0 ---> y = 3/2
∂P/∂y = 2x + 1 = 0 ---> x = -1/2
However, x and y cannot have negative values, so these values are not feasible. To find the feasible values, we can substitute the values of x and y into the cost constraint:
2(-1/2) + 3(3/2) = 0 + 9/2 = 9/2 ≤ 100
This constraint is satisfied, so the feasible allocation is x = -1/2 and y = 3/2.
To find the shadow price, we need to determine the rate at which the maximum profit would change with respect to a one-unit increase in the budget constraint. We can do this by finding the derivative of the profit function with respect to the cost constraint:
∂P/∂(2a + 3b) = λ
Where λ represents the shadow price or the marginal value of an additional dollar in the budget. In this case, λ is the shadow price.
Taking the derivative of the profit function with respect to the cost constraint:
∂P/∂(2a + 3b) = ∂(2xy - 3x + y)/∂(2a + 3b) = 0
2y - 3 = 0 ---> y = 3/2
Thus, the shadow price (λ) is 3/2 or 1.50 when rounded to two decimal places.
Learn more about maximize profit
brainly.com/question/31852625
#SPJ11
The basement in perry's house is shaped like an rectangular prism that is 28 feet long, 16 ft wide, and 8 ft high. They are going to paint everything but the floor. What is the area that will need to be painted?
Answers
Answer:
Step-by-step explanation:
Ceiling area: (28 ft)(16 ft) = 448 ft^2
End areas: 2(16 ft)(8 ft) = 256 ft^2
Long wall areas: 2(28 ft)(8 ft) = 448 ft^2
Total area (not incl. floor area) = 1152 ft^2
Which of the following describes a pattern?
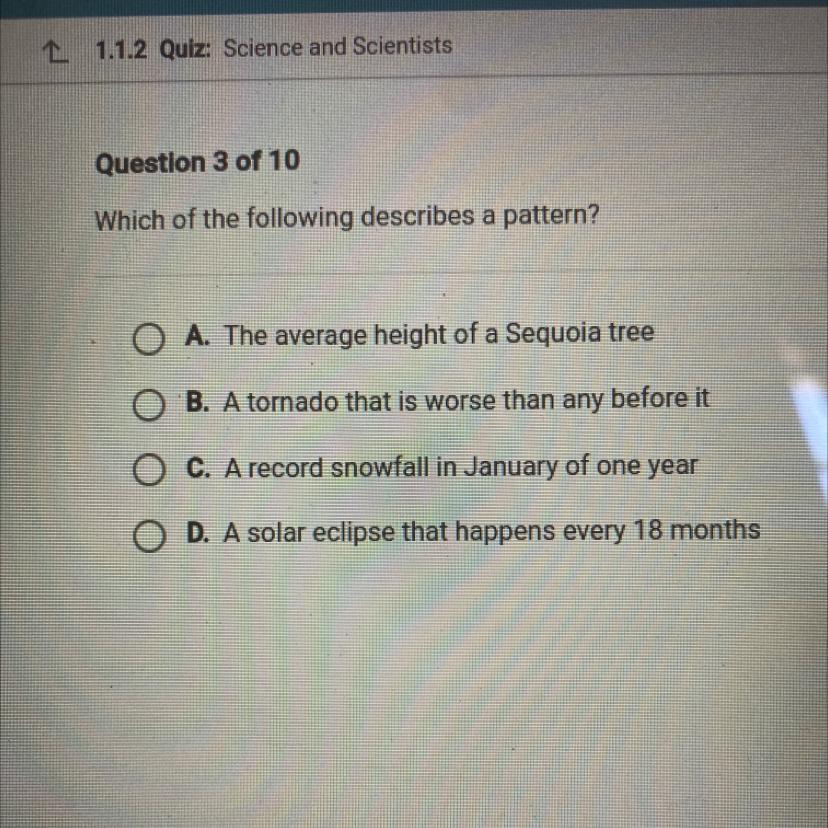
Answers
Answer:
D-a solar eclipse that happens every 18 months
Step-by-step explanation:
hope this helped helped,
have a great day!!
In an arithmetic series, the 6th term is 39 In the same arithmetic series, the 19th term is 7.8 Work out the sum of the first 25 terms of the arithmetic series.
Answers
Answer:
1,500
Step-by-step explanation:
a + 5d = 39 (1)
a + 18d = 78 (2)
Subtract (1) from (2) to eliminate a
18d - 5d = 78 - 39
13d = 39
d = 39/13
d = 3
Substitute d = 3 into (1)
a + 5d = 39 (1)
a + 5(3) = 39
a + 15 = 39
a = 39 - 15
a = 24
Sum of the first 25 terms
Sn = n/2[2a + (n – 1)d]
S25 = 25/2{2*24 + (25-1)3}
= 12.5{48 + (24)3}
= 12.5{48 + 72)
= 600 + 900
= 1,500
S25 = 1,500
Suppose 1 cast member will be picked at random from the 20 cast members who sold tickets to receive a prize. What is the probability of picking a cast member who sold more than 30 tickets
Answers
The probability of picking a cast member who sold more than 30 tickets is 2/5
Given that one cast member will be picked at random from the 20 cast members who sold tickets to receive a prize. We have to determine the probability of picking a cast member who sold more than 30 tickets.
To find the probability of picking a cast member who sold more than 30 tickets, we need to count the number of cast members who sold more than 30 tickets. Let A be the event of picking a cast member who sold more than 30 tickets. The number of cast members who sold more than 30 tickets is 8. Therefore, P(A) = 8/20 = 2/5.
The probability of picking a cast member who sold more than 30 tickets is 2/5.Answer: 2/5.
Know more about probability here:
https://brainly.com/question/31828911
#SPJ11
Help please:) and thx

Answers
Answer:
yes
Step-by-step explanation:
3 and 1/3 +[-2 and 1/4]+1 and 5/6
Answers
Answer: Hi, for these type of questions I can help you! I
Step-by-step explanation: hi, my answers are correct but wont always give you a 100%. for any questions contact me and my legal team!
If+you+invest+$100+at+an+interest+rate+of+15%,+how+much+will+you+have+at+the+end+of+eight+years?
Answers
Answer:
$305.9022863 or $305.90 (rounded to 2 decimal places)
Step-by-step explanation:
It is a compound interest, meaning an interest accumulates on an initial amount every period. The formula
A= P(1+R)^n
A= the total amount P=Initial amount R= rate n=time period
P=$100 R=15% or 0.15(decimal) n=8 (years)
A= 100 (1.15)^8
A= 100(3.059022863)
A=305.9022863
The amount you will have after 8 years is $220
Calculating simple interestThe formula for calculating simple interest is expressed as:
SI =PRT
P is the principal = $100
T is the time = 8 years
R is the rate. = 15%
SI = 100 * 8 * 0.15
SI = $120
Amount after 8years = $100 + $120
Amount after 8years = $220
Hence the amount you will have after 8 years is $220
Learn more on interest here: https://brainly.com/question/2151013
#SPJ12
Joan Deere sells tractor parts. she gets a base salary of $1255 per month
plus a commission of 8.5% of any sales greater than $10000. She sold $15000 in parts last month. (She only gets commission on the money greater than $10000), How much was her monthly check for?
Answers
Answer:
$1361.68
Step-by-step explanation:
15000 > 10000
so she gets the 8.5%
so she gets 108.5% of her salary
x/1255 = 108.5/100
1255(108.5) = 136,167.5
136,167.5/100 = 1361.68
name the property of real numbers illustrated by each equation
Answers
The property of real numbers illustrated by each equation depends on the specific equation. However, some common properties of real numbers include the commutative property, associative property, distributive property, identity property, and inverse property.
The property of real numbers illustrated by each equation depends on the specific equation. However, there are several properties of real numbers that can be applied to equations:
commutative property: This property states that the order of addition or multiplication does not affect the result. For example, a + b = b + a and a * b = b * a.associative property: This property states that the grouping of numbers in addition or multiplication does not affect the result. For example, (a + b) + c = a + (b + c) and (a * b) * c = a * (b * c).distributive property: This property states that multiplication distributes over addition. For example, a * (b + c) = (a * b) + (a * c).identity property: This property states that there exist unique elements called identity elements for addition and multiplication. For addition, the identity element is 0, and for multiplication, the identity element is 1. For example, a + 0 = a and a * 1 = a.inverse property: This property states that every real number has an additive inverse and a multiplicative inverse. The additive inverse of a number a is -a, and the multiplicative inverse of a non-zero number a is 1/a. For example, a + (-a) = 0 and a * (1/a) = 1.Learn more:About property of real numbers here:
https://brainly.com/question/30245592
#SPJ11
what are the x intercpt and y intercept of the graph of 12x-4y=48?
Answers
Answer:
X-Intercept: (4, 0), Y-Intercept: (0, -12)
lifetime of digital watch is a random variable with exponential distribution. given that the probability that the watch will work after 4 years is 0.3, find
Answers
$$f(x) = \begin{cases}\lambda e^{-\lambda x} &\quad x \geq 0\\0 &\quad x < 0\end{cases}$$where λ is the scale parameter of the distribution.
This was the probability density function (pdf) of an exponential distribution. The cumulative distribution function (cdf) is given by:$$F(x) = \begin{cases}1 - e^{-\lambda x} &\quad x \geq 0\\0 &\quad x < 0\end{cases}$$The mean and variance of an exponential distribution are:$$\mu = \frac{1}{\lambda}$$$$\sigma^2 = \frac{1}{\lambda^2}$$We are given that the lifetime of a digital watch is a random variable with exponential distribution. Let X be the lifetime of the watch and let λ be the scale parameter of the distribution. We are given that the probability that the watch will work after 4 years is 0.3. In other words, we want to find P(X > 4).Using the cdf of the exponential distribution, we have:$$P(X > 4) = 1 - P(X \leq 4) = 1 - F(4) = 1 - (1 - e^{-4\lambda}) = e^{-4\lambda}$$$$e^{-4\lambda} = 0.3$$$$-4\lambda = \ln(0.3)$$$$\lambda = \frac{\ln(0.3)}{-4} = 0.693147$$Therefore, the scale parameter of the exponential distribution is λ ≈ 0.693147. Answer more than 100 words:Given that the probability that the watch will work after 4 years is 0.3, we have found that the scale parameter of the exponential distribution is λ ≈ 0.693147. Using this value of λ, we can find the mean and variance of the lifetime of the watch. The mean is given by:$$\mu = \frac{1}{\lambda} = \frac{1}{0.693147} \approx 1.44$$Therefore, we expect the watch to last for about 1.44 years on average. The variance is given by:$$\sigma^2 = \frac{1}{\lambda^2} = \frac{1}{0.693147^2} \approx 2.00$$Therefore, the lifetime of the watch has a relatively high degree of variability, with a variance of about 2.00. In conclusion, we have found that the lifetime of a digital watch is a random variable with exponential distribution, and we have used the given probability to find the scale parameter of the distribution. We have also calculated the mean and variance of the distribution, which tell us the average lifetime of the watch and the degree of variability in its lifetime.
To know more about parameter visit:
brainly.com/question/28249912
#SPJ11
The rate parameter of the exponential distribution for the lifetime of the digital watch is 0.2663.
To find the parameters of the exponential distribution, we can use the information provided.
Let X be the lifetime of the digital watch, and λ be the rate parameter of the exponential distribution.
Given that the probability that the watch will work after 4 years is 0.3, we can use the exponential survival function:
S(t) = e^(-λt)
We know that S(4) = 0.3.
Plugging in the values, we have:
e^(-4λ) = 0.3
To solve for λ, we can take the natural logarithm (ln) of both sides:
ln(e^(-4λ)) = ln(0.3)
-4λ = ln(0.3)
Now, we can solve for λ:
λ = -ln(0.3) / 4
λ = -ln(0.3) / 4
= 0.2663
Hence, the rate parameter of the exponential distribution for the lifetime of the digital watch is 0.2663.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ4