Bob and Alice each have a bag that contains one ball of each of the colors blue, green, orange, red, and violet. Alice randomly selects one ball from her bag and puts it into Bob’s bag. Bob then randomly selects one ball from his bag and puts it into Alice’s bag. What is the probability that after this process the contents of the two bags are the same? (Hint: you can simplify your solution using "without loss of generality".)
Answers
The probability that after this process the contents of the two bags are the same is 1/30 or approximately 0.0333.
Without loss of generality, we can assume that Alice selects a ball from her bag and puts it into Bob's bag first.
At the start, there are a total of 5 balls in each bag, so the probability of Bob selecting the same ball that Alice put into his bag is 1/5. After this exchange, each bag now contains 6 balls.
Now, Alice randomly selects a ball from her bag, which has 6 balls in total. The probability of Alice selecting the same ball that Bob put into her bag is also 1/6.
To find the overall probability, we multiply the probabilities of both events occurring:
Probability = (1/5) \(\times\)(1/6) = 1/30.
Therefore, the probability that after this process the contents of the two bags are the same is 1/30 or approximately 0.0333.
For more such answers on Probability
https://brainly.com/question/251701
#SPJ8
Related Questions
3PLEASE HELP ME THIS IS URGENT I WILL GIVE BRAINLIEST
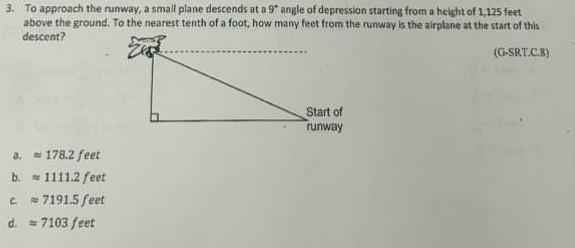
Answers
Answer: x= 7191.509 ft
Step-by-step explanation:
Sin9/1 = 1125/x
X/1 = 1125/sin9
Can someone help me solve question number 14? I've tried to solve it and got 3426 while the answers in the book say it's 2,6. Can someone pls explain why it's wrong?


Answers
Answer:
x = 2, 6
Step-by-step explanation:
differentiate f(x) using the power rule
f'(a\(x^{n}\) ) = na\(x^{n-1}\) and f'( constant) = 0
given
f(x) = x³ - 12x² + 6x - 8
f'(x) = 3x² - 24x + 6
equate f'(x) to - 30
3x² - 24x + 6 = - 30 ( add 30 to both sides )
3x² - 24x + 36 = 0 ( divide through by 3 )
x² - 8x + 12 = 0 ← in standard form
(x - 2)(x - 6) = 0 ← in factored form
equate each factor to zero and solve for x
x - 2 = 0 ⇒ x = 2
x - 6 = 0 ⇒ x = 6
solution is x = 2, 6
A construction company built a scale model of a new building. the model was built usinga scale of 3 inches= 32 feet. if the building is expected to be 200 feet tall, how tall is the model?
Answers
Answer: 18.75 inches
Step-by-step explanation:
Let the height of the model be represented by x. Therefore, based on the information given in the question, we can form an equation which will be:
3/x = 32/200
Cross multiply
32 × x = 200 × 3
32x = 600
x = 600/32
x = 18.75
Therefore, the height of the model is 18.75 inches
Which questions can be answered by the solution to the equation 3x = 27? Choose all correct answers.
Elena read three times as many pages as Noah. She read 27 pages. How many pages did Noah read?
Lin has 27 stickers. She gives 3 stickers to each of her friends. With how many friends did Lin share her stickers?
Diego paid $27 to have 3 pizzas delivered and $35 to have 4 pizzas delivered. What is the price of one pizza?
The coach splits a team of 27 students into 3 groups to practice skills. How many students are in each group?
Answers
Answer:Hi B)
Step-by-step explanation:
A manufacturer inspects 100 boxes of ice cream cones
after production to make sure no cones are cracked or
damaged. They find that 97 boxes have no defects. If
5,000 boxes of ice cream cones are being shipped to the
grocery stores, predict how many boxes will have damaged
ice cream cones.
Answers
Answer:
4850 boxes
Step-by-step explanation:
97 out of 100 boxes have no defects, can be translated into 97% of boxes have no defects. Using this number, we can find 97% of 5,000 to make an estimate of how many boxes will not have defects
.97(5,000)=4850
Sarah wants to put three paintings on her living room wall. The length of the wall is 15 feet longer than its width. The length and width of the paintings are 3 feet and 4 feet, respectively.
x ft
3 ft
(15 + x) ft
Which inequality can be used to solve for x, the height of the wall, if the combined area of the wall and the paintings is at most 202 square feet?
Answers
The inequality that can be used to solve for x, the height of the wall, is \(x^2 + 15x - 166 ≤ 0.\)
To solve for x, the height of the wall, we need to set up an inequality based on the combined area of the wall and the paintings.
The area of the wall can be represented as (15 + x) ft multiplied by the width x ft, which gives us an area of (15 + x) * x square feet.
The combined area of the wall and the three paintings is the area of the wall plus the sum of the areas of the three paintings, which are each 3 ft by 4 ft. So the combined area is (15 + x) * x + 3 * 4 * 3 square feet.
We want the combined area to be at most 202 square feet, so we can set up the following inequality:
\((15 + x) * x + 3 * 4 * 3 ≤ 202\)
Simplifying the inequality:
(15 + x) * x + 36 ≤ 202
Expanding the terms:
15x + x^2 + 36 ≤ 202
Rearranging the terms:
\(x^2 + 15x + 36 - 202 ≤ 0x^2 + 15x - 166 ≤ 0\)
Now we have a quadratic inequality. We can solve it by factoring or by using the quadratic formula. However, in this case, since we are looking for a range of values for x, we can use the graph of the quadratic equation to determine the solution.
By graphing the quadratic equation y =\(x^2 + 15x\)- 166 and finding the values of x where the graph is less than or equal to zero (on or below the x-axis), we can determine the valid range of x values.
Therefore, the inequality that can be used to solve for x, the height of the wall, is \(x^2 + 15x - 166 ≤ 0.\)
for more such question on inequality visit
https://brainly.com/question/30238989
#SPJ8
Write the equation of a line that passes through the points ( 2 , - 5 ) and ( 8 , - 2 ).
Answers
Answer:
y = 1/2x - 6
Step-by-step explanation:
y2 - y1 / x2 - x1
-2 - (-5) / 8 - 2
3 / 6
= 1/2
y = 1/2x + b
-5 = 1/2(2) + b
-5 = 1 + b
-6 = b
Angle C is inscribed in circle O.
AB is a diameter of circle O.
what is the radius of circle O?
Answers
Answer:
Step-by-step explanation:
Radius = half the diameter = AB/2
See the image below MATHH

Answers
The restricted value on the range of function f(x) is given as follows:
3.
How to obtain the domain and range of a function?The domain of a function is defined as the set containing all the values assumed by the independent variable x of the function, which are also all the input values assumed by the function.The range of a function is defined as the set containing all the values assumed by the dependent variable y of the function, which are also all the output values assumed by the function.From the horizontal dashed line, the function never assumes a value of y = 3, hence the restricted value on the range of function f(x) is given as follows:
3.
Learn more about domain and range at https://brainly.com/question/26098895
#SPJ1
Answer:
3
Step-by-step explanation:
The range of a function is the set of all possible output values (y-values).
The given diagram shows the graph of a rational function with a horizontal asymptote at y = 3 (indicated by the dashed line).
An asymptote is a line that the curve gets infinitely close to, but never touches.
Therefore, as there is an asymptote at y = 3, the curve of the function will never touch the line y = 3, and consequently the value of y = 3 is restricted from the range of the function.
What was her score on this exam, rounded to the nearest integer
Answers
Answer:
Where is the number I need to round to?
(Please don't give me a bad rating i'm trying to help :) )
find the directional derivative of the function at the given point in the direction of the vector v. g(u, v) = u2e−v, (6, 0), v = 3i 4j dvg(6, 0) =
Answers
Thus, the directional derivative of g(u, v) = u^2e^(-v) at the point (6, 0) in the direction of the vector v = 3i + 4j is -108.
To find the directional derivative of the function g(u, v) = u^2e^(-v) at the point (6, 0) in the direction of the vector v = 3i + 4j, we need to use the formula for directional derivative:
dvg(6, 0) = ∇g(6, 0) ⋅ v
where ∇g is the gradient of g, which is given by:
∇g = (∂g/∂u)i + (∂g/∂v)j
= (2ue^(-v))i - (u^2e^(-v))j
Evaluating the gradient at (6, 0), we get:
∇g(6, 0) = (2(6)e^(0))i - ((6)^2e^(0))j
= 12i - 36j
Now we can substitute these values into the formula for directional derivative:
dvg(6, 0) = ∇g(6, 0) ⋅ v
= (12i - 36j) ⋅ (3i + 4j)
= 36 - 144
= -108
Therefore, the directional derivative of g(u, v) = u^2e^(-v) at the point (6, 0) in the direction of the vector v = 3i + 4j is -108.
Know more about the directional derivative
https://brainly.com/question/30048535
#SPJ11
Frank is wanting to create a scale model of the Eiffel Tower. The real Eiffel Tower is 984 feet tall and 328 feet wide at its base. If Frank's model is 18 inches tall, how wide (in inches) must his scale model be?
Answers
Answer:
1 inch = 54.7
pls help will give brainlist

Answers
Answer:
6 lb 12 oz is the answer
Step-by-step explanation:
Just did the subtraction
what is the change of base formula
Answers
This is the formula you are looking for Logb x = Loga x/Loga b
The front suspension system of a passenger car typically has coiled springs attached to the front wheels. a typical spring has a spring constant k of about 82,000 k/m
Answers
If the front suspension system of a car has coiled springs of spring constant(k) of about 82,000N/m attached to the front wheels, then the force required to compress this spring by 1.2 cms will be 984N.
As per the question statement, the front suspension system of a passenger car has coiled springs attached to the front wheels and a typical spring has a spring constant "k" of about 82,000 k/m.
We are required to calculate the force required to compress this spring by 1.2 cms
To solve this question, we will need to apply the formula to calculate the force to compress a spring, which is known as the Hooke's Law. So, as per the Hooke's Law, the force (F) required to compress a spring of spring constant (k) by "x" units, can be represented as
[F = (k * x)]
Now comparing the RHS of the Hooke's Law equation with the data provided in the question statement, we get, (k = 82000 N/m) and
(x = 0.012 m), and using these values in the Hooke's law equation, we get, the force required to compress a spring of spring constant(k) of about 82,000N/m by 1.2 cms will be (82000 * 0.012)N = 984 N.
Spring Constant: The magnitude of force required to compress or stretch a spring by unit distance, is known as it's spring constant, and it varies from spring to spring, typically being based on the constituent elements of the spring.To learn more about Spring Constants, click on the link below.
https://brainly.com/question/14652640
#SPJ4
A paper company needs to ship paper to a large printing business. The paper will be shipped in small boxes and large boxes. The volume of each small box is 8 cubic feet and the volume of each large box is 23 cubic feet. What would be the total volume, in cubic feet, of 11 small boxes and 13 large boxes? What would be the total volume, in cubic feet, of
s
s small boxes and
l
l large boxes
Answers
Therefore 11 X 8 = 88 cubic feet form the small boxes.
23 X 13 = 299 cubic feet for the large boxes
TOTAL = SMALL + LARGE
TOTAL = 88 + 299 = 387 cubic feet
Part 2: total = small + large
Each small is 8 cubic feet and the number of small boxes is “s” so each means multiply so 8s gives us the total volume from small boxes. Large boxes are 23 each so:
Total = 8s + 23l
Select the correct answer.
Each statement describes a transformation of the graph of f(x) = x. Which statement correctly describes the graph of g(x) if g(x) = f(x-11)?
OA. It is the graph of fx) translated 11 units to the right.
OB. It is the graph of fx) where the slope is increased by 11.
OC.
It is the graph of f(x) translated 11 units up.
OD. It is the graph of f(x) translated 11 units to the left.

Answers
Using translation concepts, the statement that correctly describes the graph g(x) = f(x - 11) is given by:
A. It is the graph of f(x) translated 11 units to the right.
What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.
In this problem, we have that g(x) = f(x - 11), that is, x -> x - 11, which means that f(x) was shifted 11 units to the right and option A is correct.
More can be learned about translation concepts at https://brainly.com/question/4521517
#SPJ1
Apples cost $0.75 per pound and bananas cost $1.05 per pound.
A baker bought a total of 12 pounds of apples and bananas for $10.20.
The system of equations {a+b=120.75a+1.05b=10.20 models this situation, where a is the number of pounds of apples, and b is the number of pounds of bananas.
How many pounds of each did the baker buy?

Answers
Answer:
The baker bought 8 pounds of apples and 4 pounds of bananas.
Step-by-step explanation:
a+b=12.
0.75a+1.05b=10.20
First, multiply 2 my 10.
75a+105b=1020.
Then multiply 1 by 75.
75a+75b=900.
Then subtract.
75a+105b=1020
75a+75b=900.
75a-75a+105b-75b=1020-900
30b=120
b=4
Substitute into (1)
a+4=12
a=8.
Hope this helps :)
Find the 60th term of the arithmetic sequence-29, -49, -69,…
Answers
The 60th term of the arithmetic sequence -29, -49, -69, ... is -1209.
What is a sequence?
A sequence is an enumerated collection of objects in which repetitions are allowed. Like a set, it contains members (also called elements, or terms).
We can see that the common difference between any two consecutive terms is -20.
To find the 60th term, we can use the formula for the nth term of an arithmetic sequence:
an = a1 + (n-1)d
where an is the nth term, a1 is the first term, n is the number of the term, and d is the common difference.
In this case, we have:
a1 = -29
d = -20
n = 60
So, we can substitute these values into the formula:
a60 = -29 + (60-1)(-20)
a60 = -29 + 59(-20)
a60 = -29 - 1180
a60 = -1209
Therefore, the 60th term of the arithmetic sequence -29, -49, -69, ... is -1209.
To know more about sequence visit:
https://brainly.com/question/12246947
#SPJ1
3. Rule: output = input +29. Additional practice 7-4 use tables to represent input/output relationships
Answers
output of the given input/output relationships is 36 and 25.
What is the input-output table's rule?To illustrate a function, an input-output table can be used, as in the example below. The same function rule connects every pair of numbers in the table. To find each output number, multiply each input number (-value) by 3. ( -value).
Input-output analysis table: what is it?
The table of input-output analysis measures the flows of outputs from one industry as inputs into another (in rows) (in columns). In the input-output analysis paradigm, the original demand shift and its direct, indirect, and induced implications can be used to examine the overall economic impact of an event.
output = input +29
input= 7
output = input +29=7+29=36
input= -4
output = input +29= -4+29=25.
To know more about input-output visit:-
https://brainly.com/question/28352674
#SPJ1
The box plot below represents some data set. What is the interquartile range (IQR) of
the data?
50
100
150
200
Answers
Answer:
I think the IQR is 100
Step-by-step explanation:
You would have to find the first and third quartiles first. After that you would subtract the third quartile by the first to get the IQR
Required information In a sample of 100 steel canisters, the mean wall thickness was 8.1 mm with a standard deviation of 0.6 mm. Find a 95% lower confidence bound for the mean wall thickness. (Round the final answer to three decimal places.) The 95% lower confidence bound is Someone says that the mean thickness is less than 8.2 mm. With what level of confidence can this statement be made? (Express the final answer as a percent and round to two decimal places.) The level of confidence is %.
Answers
The lower bound of the 95% confidence interval is given as follows:
7.981 mm.
The level of confidence of the statement is of 95%.
What is a t-distribution confidence interval?The t-distribution is used when the standard deviation for the population is not known, and the bounds of the confidence interval are given according to the equation presented as follows:
\(\overline{x} \pm t\frac{s}{\sqrt{n}}\)
The variables of the equation are listed as follows:
\(\overline{x}\) is the sample mean.t is the critical value.n is the sample size.s is the standard deviation for the sample.The critical value, using a t-distribution calculator, for a two-tailed 95% confidence interval, with 100 - 1 = 99 df, is t = 1.9842.
The parameters for this problem are given as follows:
\(\overline{x} = 8.1, s = 0.6, n = 100\)
Hence the lower bound of the interval is given as follows:
8.1 - 1.9842 x 0.6/10 = 7.981 mm.
More can be learned about the t-distribution at https://brainly.com/question/17469144
#SPJ4
Please help me I not know how to do these!

Answers
Answer:58
Step-by-step explanation:
Someone help me please

Answers
The value of angle B is determined as 42 degrees.
What is the value of angle B?The value of angle B is calculated by applying Sine rule as shown below;
Sin C / length C = Sin B / length B
From the given triangle,
C = 75 degrees
B = ?
length opposite angle C = 13 yd
Length opposite angle B = 9 yd
The value of angle B is calculated as follows;
Sin B / 9 = Sin 75 / 13
13 sin B / 9 = Sin 75
13 sin B = 9 sin 75
sin B = 9/13 x sin 75
Sin B = 0.6687
B = arc sin (0.6687)
B = 42⁰
Learn more about sine rule here: https://brainly.com/question/20839703
#SPJ1
John spent 80% of his money and saved the rest. Peter spent 75% of his money and saved the rest. If they saved the same amount of money, what is the ratio of John’s money to Peter’s money? Express your answer in its simplest form.
Answers
The ratio of John's money to Peter's money is 5/4. This means if John has a total amount of 5 then Peter will have a total of 4 as his amount.
Let's assume John has 'x' amount of money, Peter has 'y' amount of money, The money John saved is 'p' and the money Peter saved is 'q'
So,
p = x - 80x/100 (equation 1)
q = y - 75y/100 (equation 2)
According to the given question, the amount John saved is equal to the amount Peter saved. Hence, we can equate equations 1 and 2.
p = q
x- 80x/100 = y - 75y/100
x - 0.8x = y - 0.75y
0.2x = 0.25y
x = 0.25y/0.2
x/y = 0.25/0.2
x/y = 25/20
x/y = 5/4
Hence, the ratio of John's money to Peter's money is 5/4.
To learn more about Ratio:
https://brainly.com/question/13419413
1. find the general solution of the system of differential equations d dt x = −37 −56 30 45
Answers
The general solution of the system of differential equations d/dt x = [-37 -56; 30 45] is:
x(t) = c1*[-4t; t]*e^(5t) + c2*[-7t; t]*e^(3t), where c1 and c2 are constants determined by the initial conditions.
To find the general solution of the system of differential equations d/dt x = [-37 -56; 30 45], we can first find the eigenvalues and eigenvectors of the matrix:
det([-37-lambda -56; 30 45-lambda]) = (-37-lambda)(45-lambda) - (-56)(30) = lambda^2 - 8lambda - 15 = (lambda-5)(lambda-3)
So the eigenvalues are lambda_1 = 5 and lambda_2 = 3.
To find the eigenvectors, we can solve for the nullspaces of the matrices A-lambda_1*I and A-lambda_2*I, where I is the identity matrix and A is the coefficient matrix:
For lambda_1 = 5, we have:
[-42 -56; 30 40] * [x1; x2] = [0; 0]
Solving this system of equations, we get x1 = -4x2. So any vector of the form [x1; x2] = [-4t; t] is an eigenvector corresponding to lambda_1 = 5.
For lambda_2 = 3, we have:
[-40 -56; 30 42] * [x1; x2] = [0; 0]
Solving this system of equations, we get x1 = -7x2. So any vector of the form [x1; x2] = [-7t; t] is an eigenvector corresponding to lambda_2 = 3.
Therefore, the general solution of the system of differential equations d/dt x = [-37 -56; 30 45] is:
x(t) = c1*[-4t; t]*e^(5t) + c2*[-7t; t]*e^(3t)
where c1 and c2 are constants determined by the initial conditions.
The correct question should be :
Find the general solution of the system of differential equations d/dt x = [-37 -56; 30 45].
To learn more about differential equations visit : https://brainly.com/question/1164377
#SPJ11
Ben asked his mother to hold
savings. At the start of June, his
savings was +$16. That month he
borrowed $20 to spend. What is
the amount remaining or owed?
Answers
Answer:
he owed $4
Step-by-step explanation:
Ben borrowed twenty dollars to spend, and 20 is above 16, so his savings is immediately gone. He owes four dollars because that's how much he needs even after using up his savings.
Emily rented a truck to move her belongings from her old apartment to her new apartment. The company charges a flat rental fee of $21.50 with an additional $0.50 for each mile driven. If the total cost was at most $121, how far did Emily drive to move her belongings to her new apartment?
A.
at least 199 miles
B.
at most 199 miles
C.
at least 60.5 miles
D.
at most 242 miles
Answers
The cost of renting the truck is $21.50, and she is charged an additional $0.50 for each mile driven. So, the total cost can be expressed as:
Total cost = $21.50 + ($0.50 * x)
According to the question, the total cost was at most $121. Therefore, we can write the inequality:
$21.50 + ($0.50 * x) ≤ $121
Now, let's solve for x:
$0.50 * x ≤ $121 - $21.50
$0.50 * x ≤ $99.50
x ≤ $99.50 / $0.50
x ≤ 199
So, Emily drove at most 199 miles. Therefore, the correct answer is B.
Answer:
B.
at most 199 miles
Step-by-step explanation:
To find how many miles Emily drove, we need to use the equation
Total cost = flat fee + miles driven * cost per mile
Substituting in the numbers
121 ≥ 21.50 + m * .5
121≥ 21.50 +.50m
Subtract 21.50 from each side.
99.50 ≥ .5m
Divide each side by .5
199 ≥m
Emily drove less than or equal to 199 miles
6.
Ahmad claims that the difference of squares method of factoring can be used even when the values aren't perfect squares. An example of his thinking is shown.

Answers
Answer:
Below.
Step-by-step explanation:
a. (x - √5)(x + √5)
= x(x + √5) - √5(x + √5)
= x^2 + √5x - √5x - 5
= x^2 - 5.
b. 10 - 3x^2
= (√10 - √3x) (√10 + √3x)
(a) Ahmad's factorization is correct.
(b) (√10 - √3x)(√10 + √3x)
Given equation as
x² - 5 = (x - √5)(x + √5)
What is a Perfect Square?
A Perfect Square is defined as when multiplying an integer by itself, we get a perfect square, which is a positive integer. In simple words, we can say that perfect squares are numbers that are the products of integers by themselves.
Solution of (a)
Taking RHS from the given equation
⇒ (x - √5)(x + √5)
⇒ x(x + √5) - √5(x + √5)
⇒ x² + √5x - √5x - 5
⇒ x² - 5.
So, RHS = LHS
Hence, Ahmad's factorization is correct.
Solution of (b)
⇒ 10 - 3x²
According to Ahmad's strategy
⇒ √10(√10 + √3x) - √3x(√10 + √3x)
⇒ (√10 - √3x)(√10 + √3x)
Learn more about perfect square here:
https://brainly.com/question/385286
#SPJ2
What two integers does sqrt41 fall between? explain reasoning
Answers
Answer:
Below!
Step-by-step explanation:
Given square root:
\(\sqrt41\)
Let's note a few perfect square roots.
\(1 = \sqrt{1 \times 1} = \sqrt{1}\)
\(2 = \sqrt{2 \times 2} = \sqrt{4}\)
\(3 = \sqrt{3 \times 3} =\sqrt{9}\)
\(4 = \sqrt{4 \times 4} =\sqrt{16}\)
\(5 = \sqrt{5 \times 5} =\sqrt{25}\)
\(6 = \sqrt{6 \times 6} =\sqrt{36}\)
\(7 = \sqrt{7 \times 7} =\sqrt{49}\)
\(8 = \sqrt{8 \times 8} =\sqrt{64}\)
And so on...
When looking at the perfect square roots we identified, we can say that:
\(\sqrt{36} < \sqrt{41} < \sqrt{49}\)
Therefore,
\(6 < \sqrt{41} < 7\)
We can conclude that \(\sqrt{41}\) is between 6 and 7.
Let's check the squares of first 10 number
1²=12²=43²=94²=165²=256²=367²=498²=649²=8110²=10041 lies between 36 and 49
Hence
√41 lies in between 6 and 7