5. For the final touches, John wanted to paint the house using 3 colors. If he has 5
gallons of paint for each color, write an equation for the total number of gallons of
paint he has?
Answers
Answer:
3 x 5 = 15
Step-by-step explanation:
To explain this in short, John has 5 gallons of 3 colors, meaning that 3 x 5 = 15 would be the appropriate equation to finish this question. I hope this helps!
Related Questions
if a linear space consists of polynomials with degrees less than 2, what is the dimension when the derivative is 0?
Answers
The dimension of V when the derivative is 0 is 1 since the l polynomial reduces to a 1-dimensional space.
The dimension of a linear space in which all polynomials with degrees less than 2 is 0 is 1. To estimate the dimension, we must take into account the basic elements of the space.
Let V be the collection of polynomials with a degree less than 2. Then the basic elements of V are 1, x
Let f(x)be a polynomial in V. Then f(x) can be written as f(x)= a0 + a1 x for some constants
We know that the derivative of f(x) is f'(x) =\(a_1$$\)
Therefore, when the derivative f'(x) is 0, it means that a1 = 0. In this case, the polynomial f(x) reduces to f(x) = a0, which is a constant.
So, the dimension of V when the derivative is 0 is 1, since the l polynomial reduces to a 1-dimensional space.
To learn more about, polynomials visit the link below:
brainly.com/question/11536910
#SPJ4
The capacity of a water tank is 10000 litres and there is 4800 litres of water. A water tap can fill 40 litres of water per minute and another tap can empty 25 litres of water per minute. If both the taps are opened together for 10 minutes, then how much water will be in the tank after 10 minutes?
Answers
The amount of water tank with water after 10 minutes will be 4950 liters.
To solve this problem, we need to keep track of the net flow of water into the tank over the course of 10 minutes. The tap filling water adds water to the tank, while the tap emptying water removes water from the tank.
Let's calculate the net flow rate of water per minute:
Flow rate = (filling tap flow rate) - (emptying tap flow rate)
Flow rate = 40 L/min - 25 L/min
Flow rate = 15 L/min
Now, we can calculate the net flow of water over 10 minutes:
Net flow of water = (flow rate) * (time)
Net flow of water = 15 L/min * 10 min
Net flow of water = 150 L
Therefore, over the course of 10 minutes, the net flow of water into the tank is 150 liters.
Initially, the tank had 4800 liters of water. Adding the net flow of water, we can determine the final amount of water in the tank:
Final amount of water = (initial amount of water) + (net flow of water)
Final amount of water = 4800 L + 150 L
Final amount of water = 4950 L
After 10 minutes, there will be 4950 liters of water in the tank.
for similar questions on water tank.
https://brainly.com/question/30723760
#SPJ8
Bob's Trees are selling trees. You have decided to buy some holiday trees to
donate to local nursing homes. They are selling for $50 each. If you have a
total of $400.00 to spend, how many trees were you able to donate?
Answers
DID YOU HEAR ABOUT... (Math photo attached)
[50 points for all answers] [comment and let me know if something is unclear in the image! (:]
![DID YOU HEAR ABOUT... (Math photo attached)[50 points for all answers] [comment and let me know if something](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/g1OjeX9e6MrHbcCx2NhzZEEcXbhM7prn.jpeg)
Answers
The values of the variable based on the equation include:
a. x = 32
b. x = 55
c. y = -18
d. m = -70
e. p = 3
f. t = 7
g. x = -11
h. n = -25
i. u = 16
j. v = 27
k. x = -9
l. w = 64
m. y = -78
n. y = 36
o. r = 5
How to compute the variables?It should be noted that an equation simply means a formula that can be used to express the equality of two expressions.
a. 1/8x = 4
x = 4 × 8
x = 32
b. 1/5x = 11
x = 5 × 11
x = 55
c. 1/9y = -2
y = -2 × 9
y = -18
d. 1/2m = -35
m = 2 × -35
m = -70
e. 6p = 18
p = 18/6
p = 3
f. 12t = 84
t = 84/12
t = 7
g. 3x = -33
x = -33/3
x = -11
h. -4n = 100
n = 100/-4
n = -25
i. -3u = -48
u = -48/-3
u = 16
j. 2v = 54
v = 54 / 2
v = 27
k. -72 = 8x
x = -72 / 8
x = -9
l. 1/4w = 16
w = 16 × 4
w = 64
m. 13 = -1/6y
y = 13 × -6
y = -78
n. -18 = -1/2y
y = -18 × -2
y = 36
o. 1/2r = 5/2
r = 5/2 × 2/1
r = 5
Learn more about equations on:
brainly.com/question/2972832
#SPJ1
The mug is 5/8 full, the mug contains 3/4 of water find the capacity of the mug
Answers
The capacity of the mug is 1.2. The capacity of the mug can be found by using the equation C = (3/4) ÷ (5/8).
What is capacity?It is the maximum amount of output that can be produced in a given period of time. Capacity is usually expressed in terms of units per unit of time, such as gallons per minute or passengers per hour.
In this equation, 3/4 represents the amount of water in the mug, and 5/8 represents the amount the mug is full.
Let the capacity of the mug be x.
Given,
Mug is 5/8 full and contains 3/4 of water
So, 5/8 of the mug is filled with water
Therefore,
5/8 of x = 3/4
(5/8 )x = (3/4)
x = (3/4) × (8/5)
x = (24/20)
x = 1.2
Therefore, the capacity of the mug is 1.2.
For more questions related to gallons
https://brainly.com/question/26007201
#SPJ1
What is the equation of the line that passes through the point (-6,8) and has a slope of -5/3? Please show step by step solution,
Answers
Answer:
The equation of the line that passes through the point (-6,8) and has a slope of -5/3 is y = (-5/3)x - 2.
Step-by-step explanation:
The equation of a line in slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.
We have the point (-6,8) and a slope of -5/3.
Step 1: Use the point-slope formula to find the equation of the line in point-slope form.
y - y1 = m(x - x1)
where x1 and y1 are the coordinates of the given point.
y - 8 = (-5/3)(x - (-6))
Simplify this equation:
y - 8 = (-5/3)(x + 6)
Step 2: Convert the equation to slope-intercept form.
Distribute (-5/3) to get:
y - 8 = (-5/3)x - 10
Add 8 to both sides:
y = (-5/3)x - 2
This is the equation of the line in slope-intercept form. Therefore, the equation of the line that passes through the point (-6,8) and has a slope of -5/3 is y = (-5/3)x - 2.
Classify. * 6x^2 - 22x^5
a. quadratic binomial
b. quadratic polynomial
c. quintic binomial
d. not a polynomial
Answers
Answer:
Step-by-step explanation:
C
If f(-2)=-4, then the point ________ is on the graph of f.
Answers
Explanation:
We have y = f(x) where x is the input and y is the output.
Any point is of the form (x,y)
Writing f(-2) means x = -2 is plugged into f(x), which results in an output of -4 because f(-2) = -4.
So we have (x,y) turn into (-2, -4)
Write this number in standard form 3 thousands, 16 tens,7 ones
Answers
244-33456/3456*345+13.55-2=
Answers
The order of operations (PEMDAS) states that we should perform multiplication and division before addition and subtraction. Using this order, we get:
244 - (33456 / 3456) * 345 + 13.55 - 2
= 244 - 97.02 * 345 + 13.55 - 2
= 244 - 33494.1 + 13.55 - 2
= -33238.55
Therefore, 244-33456/3456*345+13.55-2 = -33238.55.
help asap i need this tomorrow thanks!:)

Answers
a) The algebraic fraction \(\frac{{x + 2}}{{(x - 1)^2}}\) is proper. b) The algebraic fraction \(\frac{{4x^2 - 31x + 59}}{{(x - 4)^2}}\) can be expressed as \(-\frac{{31}}{{x - 4}} - \frac{{25}}{{(x - 4)^2}}\).
Let's solve each part step by step and determine whether the fraction is proper or improper, and then express it accordingly.
a) \(\frac{{x + 2}}{{(x - 1)^2}}\):
Step 1: Determine the degree of the numerator and the denominator:
- Degree of the numerator = 1 (linear term)
- Degree of the denominator = 2 (quadratic term)
Since the degree of the numerator is less than the degree of the denominator, the fraction is proper.
Step 2: Express the proper fraction in partial fractions:
\(\frac{{x + 2}}{{(x - 1)^2}} = \frac{A}{{x - 1}} + \frac{B}{{(x - 1)^2}}\).
Step 3: Find the values of A and B:
Multiply both sides of the equation by \(((x - 1)^2)\) to eliminate the denominators:
(x + 2) = A(x - 1) + B.
Expand the equation and collect like terms:
x + 2 = Ax - A + B.
Equate the coefficients of like terms:
Coefficient of x: 1 = A.
Constant term: 2 = -A + B.
Solve the system of equations to find the values of A and B:
From the coefficient of x, A = 1.
Substituting A = 1 into the constant term equation: 2 = -1 + B, we find B = 3.
Therefore, the partial fraction decomposition is:
\(\frac{{x + 2}}{{(x - 1)^2}} = \frac{1}{{x - 1}} + \frac{3}{{(x - 1)^2}}\).
b) \(\frac{{4x^2 - 31x + 59}}{{(x - 4)^2}}\):
Step 1: Determine the degree of the numerator and the denominator:
- Degree of the numerator = 2 (quadratic term)
- Degree of the denominator = 2 (quadratic term)
Since the degree of the numerator is equal to the degree of the denominator, the fraction is proper.
Step 2: Express the proper fraction in partial fractions:
\(\frac{{4x^2 - 31x + 59}}{{(x - 4)^2}} = \frac{A}{{x - 4}} + \frac{B}{{(x - 4)^2}}\).
Step 3: Find the values of A and B:
Multiply both sides of the equation by \(((x - 4)^2)\) to eliminate the denominators:
(4x^2 - 31x + 59) = A(x - 4) + B.
Expand the equation and collect like terms:
4x^2 - 31x + 59 = Ax - 4A + B.
Equate the coefficients of like terms:
Coefficient of \(x^2\): 4 = 0 (No \(x^2\) term on the right side).
Coefficient of x: -31 = A.
Constant term: 59 = -4A + B.
Solve the system of equations to find the values of A and B:
From the coefficient of x, A = -31.
Substituting A = -31 into the constant term equation: 59 = 4(31) + B, we find B = -25.
Therefore, the partial fraction decomposition is:
\(\frac{{4x^2 - 31x + 59}}{{(x - 4)^2}} = -\frac{{31}}{{x - 4}} - \frac{{25}}{{(x - 4)^2}}\).
The above steps provide the solution for each part, including determining if the fraction is proper or improper and expressing it in partial fractions.
For more questions on algebraic fraction:
https://brainly.com/question/11875858
#SPJ8
Find the volume of the triangular prism below.
A) 28 cubic feet
B) 168 cubic feet
C) 84 cubic feet
D) 52.5 cubic feet
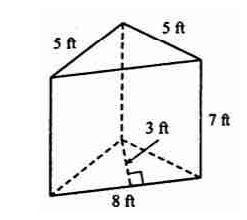
Answers
Answer:
b.168
Step-by-step explanation:
The National Weather Service keeps track of the temperature for a given day in a given city. It also keeps track of this information at certain times during a given day. The following temperatures were recorded on a January day in New York City.
Time of Day
10 AM
12 Noon
2 PM
4 PM
6 PM
8 PM
10 PM
Temperature ((Degrees Fahrenheit))
30
35
36
36
34
30
28
What is the average rate of change of temperature with respect to time over the evening hours from 6 PM to 10 PM? Interpret this value in a complete sentence.
a.
6 degrees Fahrenheit degrees per hour; The temperature drops at an average rate of 6 degrees per hour from 6 PM to 10 PM.
b.
Negative 6 degrees Fahrenheit degrees per hour; The temperature drops at an average rate of 6 degrees per hour from 6 PM to 10 PM.
c.
Negative 1.5 degrees Fahrenheit degrees per hour; The temperature drops at an average rate of 1.5 degrees per hour from 6 PM to 10 PM.
d.
1.5 degrees Fahrenheit degrees per hour; The temperature drops at an average rate of 1.5 degrees per hour from 6 PM to 10 PM.
Answers
The average rate of change of the temperature from 6 to 10 pm is given as -1.5. Option C is correct
How to solve for the rate of changeFrom 6 pm to 10 pm we have a total of 4 hours that is in between this period of time.
From the table the temperature at 6 pm is 34, the temperature at 10 pm is 28 degrees
Such that we would have:
\(\frac{28-34}{4}\)
= -6 / 4
= - 1.5
Hence we would have that Negative 1.5 degrees Fahrenheit degrees per hour; The temperature drops at an average rate of 1.5 degrees per hour from 6 PM to 10 PM.
Read more on rate of change here:https://brainly.com/question/29055843
#SPJ1
which expression is equivalent to n+n-0.18n
a. 1.18n
b. 1.82n
c. n- 0.18
d. 2n - 0.82
Answers
Answer:
Simplifying the expression `n + n - 0.18n`, we get:
n + n - 0.18n = 2n - 0.18n
Therefore, the expression `n + n - 0.18n` is equivalent to `2n - 0.18n`.
Looking at the answer choices:
a. 1.18n
b. 1.82n
c. n- 0.18
d. 2n - 0.82
We can see that choice d is equivalent to the simplified expression `2n - 0.18n`.
Therefore, the answer is d. 2n - 0.82.
Step-by-step explanation:
. Bert has a well-shuffled standard deck of 52 cards, from which he draws one card; Ernie has a 12-sided die, which he rolls at the same time Bert draws a card. Compute the probability that:
a. Bert gets a Jack and Ernie rolls a five.
b. Bert gets a heart and Ernie rolls a number less than six.
c. Bert gets a face card (Jack, Queen or King) and Ernie rolls an even number.
d. Bert gets a red card and Ernie rolls a fifteen.
e. Bert gets a card that is not a Jack and Ernie rolls a number that is not twelve.
Answers
Therefore , the solution of the given problem of probability comes out to be a)1/78 ,b)65/624 ,c)1/4 ,d)0 and e)12/13.
What is probability, exactly?The basic goal of any considerations technique is to assess the probability that a statement is accurate or that a specific incident will occur. Chance can be represented by any number range between 0 and 1, where 0 normally indicates a percentage but 1 typically indicates the level of certainty. An illustration of probability displays how probable it is that a specific event will take place.
Here,
a.
P(Bert gets a Jack and Ernie rolls a five) = P(Bert gets a Jack) * P(Ernie rolls a five)
= (4/52) * (1/12)
= 1/78
b.
P(Bert gets a heart and Ernie rolls a number less than six) = P(Bert gets a heart) * P(Ernie rolls a number less than six)
= (13/52) * (5/12)
= 65/624
c.
P(Bert gets a face card and Ernie rolls an even number) = P(Bert gets a face card) * P(Ernie rolls an even number)
= (12/52) * (6/12)
= 1/4
d.
P(Bert gets a red card and Ernie rolls a fifteen) = 0
e.
Ernie rolls a number that is not twelve, and Bert draws a card that is not a Jack:
A regular 52-card deck contains 48 cards that are not Jacks,
so the likelihood that Bert will draw one of those cards is 48/52, or 12/13.
On a 12-sided dice with 11 possible outcomes,
Ernie rolls a non-12th-number (1, 2, 3, etc.).
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
According to the box and whisker plot, what was the maximum number of hot dogs eaten in the hot dog eating contest?

Answers
Answer:
Step-by-step explanation:
It will be 18
0 8. A function f(x) is said to have the jump discontinuity at a point x = a if lim a)x+a+ c) x→a+ f(x) = lim x→a+ f(x) = lim x→a¯ lim X-a f(x). b) lim x→a f(x) = lim x→a¯ _ f(x) f(x) = f(a) d) lim f(x) → +00 x→a+
Answers
The correct option for the given question is c) lim x→a¯ f(x) = f(a) when the function f(x) is said to have jump discontinuity at a point x=a.
What is jump discontinuity?Jump continuity is a concept in calculus that describes the behaviour of a function at a specific point where the function jumps from one value to another value without any intermediate values. In other words, a function is considered jump continuous at a point if the function approaches a finite limit from both the left and right sides of that point, but the function values on the left and right sides of the point are not equal.
According to the given information:
The correct notation for the left-hand limit as x approaches a from the left side is lim x→a¯, where the horizontal line above the "a" indicates approaching from the left side.
The statement "lim x→a¯ f(x) = f(a)" means that the limit of f(x) as x approaches a from the left side is equal to the value of f(a) at x = a. This indicates that the function f(x) has a jump discontinuity at x = a, where the function jumps from one value to another value at that specific point.
To know more about jump discontinuity visit: https://brainly.com/question/12644479
#SPJ1
i need these done as quick as possible and i have no clue what to do.

Answers
Answer:
1. y = 4
2. x = 10
3. n = 6
4. m = 4
5. h = 2
Step-by-step explanation:
Hope this helps!!
Number two is (2)
Number three (3)
Number four (4)
Number five (11)
I think that how you do it
Which of the following is a solution to this inequality?
y<2/3x+2
(0, 3)
(−3, 1)
(3, 5)
(1, 2)
Answers
Answer:
(d) (1, 2)
Step-by-step explanation:
You want to know which of the given points satisfies the inequality.
GraphWe find it easiest to plot the given points on a graph of the solution. This shows us that (1, 2) is a solution to the inequality. (It lies in the solution area.)
__
Additional comment
Another way to choose the answer is to try each of the points in the inequality.
If you can visualize the boundary line (without plotting it) as a line with positive slope and a y-intercept of 2, you can more readily reject the first choice and accept the last choice. (0, 3) is above the y-intercept, and (1, 2) is to the right of it (in the solution space).
You may also recognize the x-intercept will be -3, so the second choice lies above the boundary line.

11. Which one of the following is unique? b. mode a. Mean c. Median d. A and B
Answers
Among the mean, mode, and median, the unique one is the b. mode.
What is the mode?The mode is the data value that occurs many times more than other data values.
Unlike the mean that shows the average value of all the data values, the mode occurs more. While we compute the mean by dividing the total data value by the number of data items, the mode is not computed but found as the most frequent data value.
Similarly, the median can be computed when two values occur as the middle values.
Thus, among the three measures of central tendency, the mean, the median, and the mode, the mode is the most unique since it is not computed.
Learn more about the measures of central tendency at https://brainly.com/question/28101345.
#SPJ1
How many meters are equal to 18 kilometers?
Answers
Answer:
18000
Step-by-step explanation:
The number of meters in 18 kilometers is 18,000 meters(m)
How to convert meters to kilometers1900 meter(m) = 1 kilometer(km)x meters = 18 kilometers
x meters = 18 kilometers × 1000
x = 18,000 meters
Therefore, 18 kilometers is equivalent to 18,000 meters
learn more about conversion:
https://brainly.com/question/9032119
Please help me answer this

Answers
Answer:
I really do not know
Step-by-step explanation:
Franco, Ivanna, and Esther bought school supplies.
Each person spent between $8 and $13.
Franco bought 6 items.
Ivanna bought 3 items.
Esther bought 4 items.
The prices of the items are given below. Drag items to each box to show what each person could have bought.
Answers
So I think I had this for Imagine Math, so here is what I got :D;
Franco (6 items): 6 notebooks = 1.89+1.89+1.89+1.89+1.89+1.89= 11.34
Ivanna (3 items): 1 colored thingy + 2 sharped thingy = 4.29+2.45+2.45= 9.19
Esther (4 items): 1 colored thingy + notebook + sharpened thingy = 1.89+2.45+0.54+4.29= 9.17
I really hope this helps :DDDDDDDD
a) angle of line of From a point O in the school compound, Adeolu is 100 m away on a bearing N 35° E and Ibrahim is 80 m away on a bearing S 55° E. (a) How far apart are both boys? (b) (c) What is the bearing of Adeolu from point O, in three-figure bearings? What is the bearing of Ibrahim from point O, in three figure bearings? A boy walks 5 km due North and then 4 km due East. (a) Find the bearing of his current posi- tion from the starting point. (b) How far is the boy now from the start- ing point? A boy runs 200 m on a bearing of 230°.
Answers
a) Angle of line of sightFrom a point O in the school compound, Adeolu is 100 m away on a bearing N 35° E and Ibrahim is 80 m away on a bearing S 55° E. (a) How far apart are both boys? (b) (c) What is the bearing of Adeolu from point O, in three-figure bearings? What is the bearing of Ibrahim from point O, in three-figure bearings?The angle of the line of sight of Adeolu from the point O is given by:α = 90 - 35α = 55°.The angle of the line of sight of Ibrahim from the point O is given by:β = 90 - 55β = 35°.a) By using the Sine Rule, we can determine the distance between Adeolu and Ibrahim as follows:$
\frac{100}{sin55^{\circ}} = \frac{80}{sin35^{\circ}
100 sin 35° = 80 sin 55°=57.73 mT
herefore, both boys are 57.73 m apart. b) The bearing of Adeolu from the point O can be determined as follows:OAN is a right-angled triangle with α = 55° and OA = 100. Therefore, the sine function is used to determine the side opposite the angle in order to determine AN.
Thus:$$sin55^{\circ} = \frac{AN}{100}$$AN = 80.71 m.
To find the bearing, OAD is used as a reference angle. Since α = 55°, the bearing is 055°.
Therefore, the bearing of Adeolu from the point O is N55°E. c) Similarly, the bearing of Ibrahim from the point O can be determined as follows:OBS is a right-angled triangle with β = 35° and OB = 80. Therefore, the sine function is used to determine the side opposite the angle in order to determine BS.
Thus:$$sin35^{\circ} = \frac{BS}{80}$$BS = 46.40 m.
To find the bearing, OCD is used as a reference angle. Since β = 35°, the bearing is 035°.Therefore, the bearing of Ibrahim from the point O is S35°E. A boy walks 5 km due North and then 4 km due East. (a) Find the bearing of his current posi- tion from the starting point.
(b) How far is the boy now from the start- ing point?The boy's position is 5 km North and 4 km East from his starting position. The Pythagorean Theorem is used to determine the distance between the two points, which are joined to form a right-angled triangle. Thus
:$$c^2 = a^2 + b^2$$
where c is the hypotenuse, and a and b are the other two sides of the triangle. Therefore, the distance between the starting position and the boy's current position is:$$
c^2 = 5^2 + 4^2$$$$c^2 = 25 + 16$$$$c^2 = 41$$$$c = \sqrt{41} = 6.4 km$$
Therefore, the boy is 6.4 km from his starting point. (a) The bearing of the boy's current position from the starting point is given by the tangent function.
Thus:$$\tan{\theta} = \frac{opposite}{adjacent}$$$$\tan{\theta} = \frac{5}{4}$$$$\theta = \tan^{-1}{\left(\frac{5}{4}\right)}$$$$\theta = 51.34^{\circ}$$
Therefore, the bearing of the boy's current position from the starting point is N51°E.
For such more question on triangle
https://brainly.com/question/1058720
#SPJ8
NO LINKS!! URGENT HELP PLEASE!!!
NOT MULTIPLE CHOICE!!
8. a. Finish the table
b. Name the type of sequence
c. Find the equation for the following sequence

Answers
Answer:
7: 63
8: 73
arithmetic sequence
y = 10x - 7
or f(n) = 10x -7
or
\(a_{n}\) = 3 + (n-1)10
Step-by-step explanation:
the output increases by 10 every time that the input increases by 1. That gives us our common difference or slope. The y intercept is -7. That is the value is you worked backwards until you get to n = 0. The initial value is 3. That is when n is 1.
When n is 3, f(n) is 23
When n is 2, f(n) is 13
When n is 1, f(n) is 3
When n is 0, f(n) is -7
I am not sure if this is clear. I am assuming that you have a lot of knowledge of linear equations and how to write arithmetic sequence. If my explanation is confusing it is me and not you.
Answer:
a. 63,73
b. Arithmetic sequence
c.t(n)=10n-7
Explanation:
a. Here is the completed table:
n | t(n)
4 | 33
5 | 43
6 | 53
7 | 63
8 | 73
b.
The type of sequence is arithmetic.
An arithmetic sequence is a sequence of numbers where the difference between any two consecutive terms is constant.
In this case, the difference between any two consecutive terms is 10.
c.
The equation for the arithmetic sequence is:
t(n)=a+(n-1)d
where:
t(n) is the nth term in the sequencen is the term numberd is the common differencea is the first termFor Question:
d=43-33=10a=?Now
equation becomes:
t(4) = a+(4-1)10
33=a+30
a=33-30
a=3
Now, the Equation becomes
t(n) = 3+(n-1)10
t(n) = 3+10n-10
t(n)=10n-7
Seth is using the figure shown below to prove Pythagorean Theorem using triangle similarity:
In the given triangle ABC, angle A is 90° and segment AD is perpendicular to segment BC.
The figure shows triangle ABC with right angle at A and segment AD. Point D is on side BC.
Which of these could be a step to prove that BC2 = AB2 + AC2?
possible answers -
By the cross product property, AB2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by AD.
By the cross product property, AB2 = BC multiplied by AD.

Answers
The correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
To prove that \(BC^2 = AB^2 + AC^2\), we can use the triangle similarity and the Pythagorean theorem. Here's a step-by-step explanation:
Given triangle ABC with right angle at A and segment AD perpendicular to segment BC.
By triangle similarity, triangle ABD is similar to triangle ABC. This is because angle A is common, and angle BDA is a right angle (as AD is perpendicular to BC).
Using the proportionality of similar triangles, we can write the following ratio:
\($\frac{AB}{BC} = \frac{AD}{AB}$\)
Cross-multiplying, we get:
\($AB^2 = BC \cdot AD$\)
Similarly, using triangle similarity, triangle ACD is also similar to triangle ABC. This gives us:
\($\frac{AC}{BC} = \frac{AD}{AC}$\)
Cross-multiplying, we have:
\($AC^2 = BC \cdot AD$\)
Now, we can substitute the derived expressions into the original equation:
\($BC^2 = AB^2 + AC^2$\\$BC^2 = (BC \cdot AD) + (BC \cdot AD)$\\$BC^2 = 2 \cdot BC \cdot AD$\)
It was made possible by cross-product property.
Therefore, the correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
For more questions on cross-product property:
https://brainly.com/question/14542172
#SPJ8
A residential community was polling households to find out whether they wanted to get their TV signal from a satellite or cable. The results are shown in the Venn diagram.
A circle labeled satellite 55 overlaps a circle labeled cable 75. Overlap is labeled 12. 4-column table with 3 rows. First column has no label with entries satellite, not satellite, total. Second column is cable with entries blank, 51%, blank. Third column is not cable with entries a, b, blank. Fourth column is labeled total with entries blank, blank, 100%.
What are the values of a and b in the relative frequency table for the survey results? Round answers to the nearest percent.
a = 82%, b = 3%
a = 38%, b = 50%
a = 38%, b = 3%
a = 93%, b = 19
Answers
The correct answer is:
a = 43%
b = 88%
To determine the values of a and b in the relative frequency table, we need to analyze the information provided in the Venn diagram and the given table.
From the Venn diagram, we can gather the following information:
The circle labeled "satellite" has a value of 55.
The circle labeled "cable" has a value of 75.
The overlap between the two circles is labeled as 12.
Using this information, we can complete the table:
First column - "Satellite":
Entries: Satellite, Not satellite, Total
Total: 55 (as given in the Venn diagram)
Second column - "Cable":
Entries: Blank, 51%, Blank
To find the value for the "Cable" entry, we need to subtract the overlap (12) from the total number of cable users (75).
Cable: 75 - 12 = 63
Therefore, the entry becomes: Blank, 51%, Blank
Third column - "Not Cable":
Entries: a, b, Blank
To find the value for "a," we subtract the overlap (12) from the total number of satellite users (55).
a: 55 - 12 = 43
To find the value for "b," we subtract the overlap (12) from the total number of households (100).
b: 100 - 12 = 88
Therefore, the entries become: 43, 88, Blank
Fourth column - "Total":
Entries: Blank, Blank, 100%
The total number of households is given as 100% (as stated in the question).
Therefore, the values of a and b in the relative frequency table are:
a = 43% (rounded to the nearest percent)
b = 88% (rounded to the nearest percent)
Hence, the correct answer is:
a = 43%
b = 88%
for such more question on values
https://brainly.com/question/27746495
#SPJ8
What is the slant height of the cone?

Answers
The slant height of the cone is 12.6 units
What are solids ?
A three-dimensional object that is closed (which may, according to some terminology conventions, be self-intersecting). A solid is any constrained area of space that is bounded by surfaces, according to Kern and Bland (1948, p. 18). The sphere, cube, cone, and cylinder, as well as the polyhedra more broadly, are some of the most basic solids.
h= 12
diameter = d = 8
so, radius, r = d/2 = 8/2 = 4
Formula for slant height , l is:
l = √(h² + r²) = √(12² + 4² )
= √(144 + 16) = √160 = 12.649 ≈ 12.6 units
The slant height of the cone is 12.6 units
To learn more about the solids from the given link
https://brainly.com/question/25727148
#SPJ1
4(6)^x 864 for x answer for x
Answers
Answer:
x = 3
Step-by-step explanation:
Maybe you want the value of x such that ...
4(6^x) = 864
SolutionDividing by 4 gives ...
6^x = 216
You may know that 216 = 6^3. Using that, we can equate exponents:
6^x = 6^3
x = 3
Alternatively, we can use logarithms to find x. Taking logs gives ...
x·log(6) = log(216)
x = log(216)/log(6) = 3
Find the area of 11 by 2
Answers
11cm x 2cm = 22