8. Which of the following is a predictive model? A. clustering B. regression C. summarization D. association rules 9. Which of the following is a descriptive model? A. regression B. classification C.
Answers
8. The correct option for a predictive model is:
B. regression
9. The correct option for a descriptive model is:
B. classification
Predictive models are those that attempt to predict the value of a certain target variable, given the input variables. The input variables, often known as predictors, are used to determine the target variable, also known as the response variable. Predictive models are often referred to as regression models. Therefore, regression is a predictive model
Descriptive models are those that attempt to describe or summarize the data in some way. They don't make predictions or estimate values for specific variables. Rather, they're used to categorize, classify, or group data in a useful way. Classification, for example, is a descriptive modeling technique that groups data into discrete categories based on specific characteristics. As a result, classification is a descriptive model.
To know more about regression, visit the link :
#SPJ11
Related Questions
Select all (there are more than one) that are solutions to the system of linear inequalities graphed below:

Answers
The solutions are all the points inside the shaded region:
(1, 0.5) , (2,-1) and (2.5, -2)

Expand and simplify (x + 3)(x-4)
Answers
Answer:
2x -1
Step-by-step explanation:
x*x =2x 3-4 =-1
2x+-4
3 over 3 fourths divided by 5 over 7
Answers
Answer:
5.6
Step-by-step explanation:
(3÷3/4)÷5/7
\( \frac{3 \times 4}{3} \div \frac{5}{7} \)
\(4 \div \frac{5}{7} \)
\(4 \times \frac{7}{5} \)
\( \frac{28}{5} \)
=5.6
use "keep, change, flip " when dividing a number by a fraction.
keep the whole number
flip the divide sign to multiply
change the placement of number e.g. 5/7 becomes 7/8
then solve
Helps me solve this problem please

Answers
Answer:
I Think D.
Step-by-step explanation:
Please help me! It’s for geometry

Answers
The answer to this is 2 67.5
PLZ HELP!!! I’ll give brainly !!!!!

Answers
Answer:
(3,-2)
Step-by-step explanation:
The vertex is the lowest point of the arc!
Hope I helped!
I need help please I don’t really understand

Answers
Answer:
hi now i ain't too sure but its C
Step-by-step explanation:
since we r adding it will move to the right side 2 blocks then we go down 5 since its minus
SEE QUESTION IN IMAGE

Answers
Answer:
46.Total number in favour:
128 + 96 = 224Probability:
P(favour, A) = 128/224 = 4/747.Total number in against:
32 + 48 = 80Probability:
P(against, not B) = 32/80 = 2/5Are my answers correct? Will give points if not correct can you solve please

Answers
The area of the smaller sector or minor sector is 125.66 yd².
The area of the larger sector or major sector is 326.73 yd².
What are the areas of the sector?The areas of the minor and major sectors is calculated by applying the following formulas follow;
Area of sector is given as;
A = (θ/360) x πr²
where;
r is the radius of the sectorθ is the angle of the sectorThe area of the smaller sector or minor sector is calculated as follows;
A = ( 100 / 360 ) x π ( 12 yd)²
A = 125.66 yd²
The area of the larger sector or major sector is calculated as follows;
θ = 360 - 100
θ = 260⁰
A = ( 260 / 360 ) x π ( 12 yd)²
A = 326.73 yd²
Learn more about area of sector here: https://brainly.com/question/30607726
#SPJ1
5. Lines and m are perpendicular. A point Q has this
property: rotating Q 180 degrees using center P has the
same effect as reflecting Q over line m.
a. Give two possible locations of Q.
B. Do all points in the plane have this property?
Answers
It should be noted that rotating Q 180 degrees using the center P has the same effect as reflecting Q over the Line M due to the fact that Lines L and M are perpendicular lines.
Want are perpendicular lines?It should be noted that perpendicular lines are the lines that intersect at a 90-degree angle. When two non-vertical lines are in the same plane and intersect at a right angle, they are said to be perpendicular.
It should be noted that horizontal and vertical lines are simply perpendicular to each other that is, the axes of the coordinate plane. Also, the slopes of the perpendicular lines are negative reciprocals.
Based on the information, rotating Q 180 degrees from the center will be similar to reflecting Q over any of the perpendicular lines. Note that an overview was given as the information wasn't complete.
Learn more about perpendicular lines on:
https://brainly.com/question/1202004
#SPJ1
If X has an exponential (1) PDF, what is the PDF of W = X2? 5.9.1 Random variables X and Y have joint PDF fx,y(, y) = ce -(x²/8)–(42/18) What is the constant c? Are X and Y in- dependent? 6.4.1 Random variables X and Y have joint PDF fxy(x, y) = 6xy 0
Answers
The answer of 1. The probability density function (PDF) of \(W = X^2\) when X has an exponential (1) PDF and 2. The X and Y are dependent random variables.
The PDF of \(W = X^2\), where X has an exponential (1) distribution, is given by \(\lambda e^{(-\lambda \sqrt w)} * 1/(2w^{(1/2)})\). X and Y are dependent random variables based on their joint PDF.
1. If X has an exponential (1) probability density function (PDF), we can find the PDF of \(W = X^2\) using the method of transformations.
Let's denote the PDF of X as fX(x). Since X has an exponential (1) distribution, its PDF is given by:
\(fX(x) = \lambda e^{(-\lambda x)}\)
where λ = 1 in this case.
To find the PDF of \(W = X^2\), we need to apply the transformation method. Let \(Y = g(X) = X^2\). The inverse transformation is given by X = h(Y) = √Y.
To find the PDF of W, we can use the formula:
fW(w) = fX(h(w)) * |dh(w)/dw|
Substituting the values:
fW(w) = fX(√w) * |d√w/dw|
Taking the derivative:
d√w/dw = 1/(2√w) = \(1/(2w^{(1/2)})\)
Substituting back into the equation:
\(fW(w) = fX(\sqrt w) * 1/(2w^{(1/2)})\)
Since fX(x) = \(\lambda e^{(-\lambda x)}\), we have:
fW(w) = \(\lambda e^{(-\lambda x)}\) \(* 1/(2w^{(1/2))}\)
This is the probability density function (PDF) of \(W = X^2\) when X has an exponential (1) PDF.
2. To find the constant c for the joint probability density function (PDF) fx,y(x, y) = \(ce^{(-(x^2/8) - (4y^2/18))\), we need to satisfy the condition that the PDF integrates to 1 over the entire domain.
The condition for a PDF to integrate to 1 is:
∫∫ f(x, y) dx dy = 1
In this case, we have:
∫∫ \(ce^{(-(x^2/8) - (4y^2/18)) }dx dy = 1\)
To find the constant c, we need to evaluate this integral. However, the limits of integration are not provided, so we cannot determine the exact value of c without the specific limits.
Regarding the independence of X and Y, we can determine it by checking if the joint PDF fx,y(x, y) can be factored into the product of individual PDFs for X and Y.
If fx,y(x, y) = fx(x) * fy(y), then X and Y are independent random variables.
However, based on the given joint PDF fx,y(x, y) = \(ce^{(-(x^2/8) - (4y^2/18))\), we can see that it cannot be factored into separate functions of X and Y. Therefore, X and Y are dependent random variables.
To learn more about exponential from the given link
https://brainly.com/question/30241796
#SPJ4
hello, can i please get some please on this one ASAP! i will mark as BRAINLIEST!!

Answers
Answer:
\((x+6)(x-6)\)
Step-by-step explanation:
Hi there!
The difference of squares theorem states that \(a^2-b^2=(a+b)(a-b)\).
We're given:
\(x^2-36\)
This can be rewritten since 36 is a perfect square:
\(=x^2-6^2\)
Use the difference of squares theorem:
\(=(x+6)(x-6)\)
I hope this helps!
Answer:
(x-6)(x+6)
Step-by-step explanation:
x^2 -36
Rewriting
x^2 - 6^2
We know a^2 - b^2 = (a-b)(a+b)
(x-6)(x+6)
let n be the number of 5-digit sequences that have a digit that appears at least 3 times. find the remainder when is divided by 1000.
Answers
The number of sequences cannot be negative, we take the remainder when -11750 is divided by 1000, which is 250. The answer is 250.
To solve the problem, we will use the principle of inclusion-exclusion. Let A be the set of 5-digit sequences that have at least one digit that appears 3 times, and let B be the set of 5-digit sequences that have at least one digit that appears 4 or 5 times.
We first count the size of set A. There are 10 choices for the digit that appears 3 times, and 4 choices for its location in the sequence. For the remaining 2 digits, there are 10 choices each. Thus, the size of A is 10 * 4 * 10 * 10 = 4000.
Next, we count the size of set B. There are 10 choices for the digit that appears 4 or 5 times, and 5 choices for its location in the sequence. For the remaining digit, there are 9 choices. Thus, the size of B is 10 * 5 * 9 = 450.
However, some sequences have a digit that appears both 3 times and 4 or 5 times. To count these sequences, we choose the repeated digit first, and then choose its location. There are 10 choices for the repeated digit, and 4 choices for its location. For the remaining 2 digits, there are 9 choices each, and 5 choices for their location. Thus, the size of the intersection of A and B is 10 * 4 * 9 * 9 * 5 = 16200.
By inclusion-exclusion, the number of 5-digit sequences that have a digit that appears at least 3 times is |A ∪ B| = |A| + |B| - |A ∩ B| = 4000 + 450 - 16200 = -11750. However, since the number of sequences cannot be negative, we take the remainder when -11750 is divided by 1000, which is 250.
Therefore, the answer is 250.
Learn more about remainder here
https://brainly.com/question/29347810
#SPJ11
I need help on this giving brainlist ASAP

Answers
Answer:
no solution
Step-by-step explanation:
|x| = -10
Absolute value means that it is positive or 0
It cannot be negative
There is no solution
Step-by-step explanation:
There is no solution
|A|
can be only 0 or positive number
can't be -
from the rule of Mathematics
The mean life of a television set is 121 months with a variance of 256. If a sample of 95 televisions is randomly selected, what is the probability that the sample mean would be less than 118.8 months?
Answers
We can calculate the probability that the sample mean would be less than 118.8 months by standardizing the sample mean using the z-score and consulting the standard normal distribution.
To calculate the z-score, we need to calculate the standard deviation of the sampling distribution of the sample mean, also known as the standard error. The standard error is the square root of the variance divided by the square root of the sample size. In this case, the variance is 256, and the sample size is 95, so the standard error is √(256/95) ≈ 2.693.
Next, we calculate the z-score using the formula z = (x - μ) / σ, where x is the desired value (118.8 months), μ is the population mean (121 months), and σ is the standard error (2.693). Plugging in the values, we get z = (118.8 - 121) / 2.693 ≈ -1.013.
Finally, we find the probability that the sample mean is less than 118.8 months by looking up the z-score in the standard normal distribution table or using statistical software. From the table or software, we find that the probability corresponding to a z-score of -1.013 is approximately 0.1562.
Therefore, the probability that the sample mean would be less than 118.8 months is approximately 0.1562 or 15.62%.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
relative maxima and relative minima of the function f(x) = x^5 - 4x^3 + 3x^2 - 8x - 6
Answers
The relative maxima and relative minima of the function
f(x) = x^5 - 4x^3 + 3x^2 - 8x - 6
the relative maxima is -1.871the relative minima is 1.518How to fine the relative maxima and minimaThe relative minima and maxima is calculated
by differentiating the given function find the critical values or roots of the equationdifferentiate the second tiesubstitute the critical value that are real numbersthe critical value that gave a negative value is the maximathe critical value that gave a positive value is minimaThe procedure is done as follows
x^5 - 4x^3 + 3x^2 - 8x - 6
differentiating gives
5x^4 - 12x^2 + 6x - 8
solving the equation for the critical values are
x₁ = 0.176 + 0.73i
x₂ = 0.176 - 0.73i
x₃ = 1.518
x₄ = -1.871
The second derivative
5x^4 - 12x^2 + 6x - 8
differentiating gives
20x^3 - 24x + 6
substituting x = 1.58
20 * 1.58^3 - 24 * 1.58 + 6
= 46.966 (positive hence minima)
substituting x = -1.871
20 * -1.871^3 - 24 * -1.871 + 6
= -169.9 (negative hence maxima)
Learn more about relative maxima and minima at:
https://brainly.com/question/6422517
#SPJ1
Can someone help me with number 13 I need the equation fast

Answers
The expression is given as
\((-2+7i)(-1-6i)(6+3i)\)Solve and simplify the expression by opening the brackets
\((2+12i-7i-42i^2)(6+3i)\)\((2+5i+42)(6+3i)=(5i+44)(6+3i)_{}\)\(30i+15i^2+264+132i\)\(162i+264-15=162i+249\)Hence the answer is
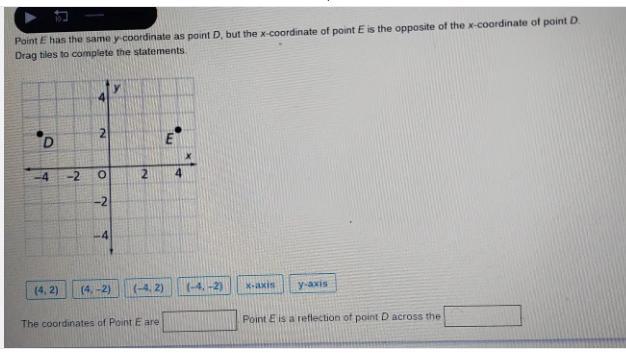
\(162i+249\)Point E has the same y-coordinate as point D, but the x-coordinate of point D. Plot point E and write the coordinates of point E. Then describe the type of reflection you plotted.
Answers
The coordinates of Point E are (-4,2) and Point E is a reflection of point D across the X-axis.
What is the coordinate about?Point E has the same y-coordinate as point D, which is 2. However, the x-coordinate of point E is the opposite of the x-coordinate of point D. The x-coordinate of point D is 4, so the x-coordinate of point E must be -4. Therefore, the coordinates of Point E are (-4,2).
As for the reflection, you can imagine a mirror placed on the x-axis (horizontally) and Point D and E being on the same side of that mirror.
Therefore, As Point D is reflected on the mirror, it will be flipped and the x-coordinate changes its sign and becomes -4. Therefore Point E is a reflection of point D across the X-axis.
Read more about coordinate
https://brainly.com/question/27749090
#SPJ1
See full question below
Point E has the same y-coordinate as point D, but the x-coordinate of point E is the opposite of the x- coordinate of point D. Drag tiles to complete the statements. (4,2) (4,-2) (-4,2) (-4,-2) X-axis y-axis The coordinates of Point E are --- &Point E is a reflection of point D across the ---
he following problems add in a minimal threshold value for the species to survive, T, which changes the differential equation to
P't = rp(1-P/K) (1-T/P)
Bengal tigers in a conservation park have a carrying capacity of 100 and need a minimum of 10 to survive. If they grow in population at a rate of 1% per year, with an initial population of 15 tigers, solve for the number of tigers present.
Answers
the solution for the number of tigers present over time is given by:
P - (P^2)/(2K) - (T/K)P + (T/K)ln(P) = rt + 11.375 + 0.1ln(15)
To solve the given differential equation for the population of Bengal tigers in the conservation park, we'll use the given parameters and initial conditions.
The differential equation for the population (P) is:
P't = rp(1 - P/K)(1 - T/P)
Given:
Carrying capacity (K) = 100
Minimum threshold value for survival (T) = 10
Population growth rate (r) = 1% = 0.01 (per year)
Initial population (P0) = 15
Now, let's solve the differential equation to find the number of tigers present over time.
Separating variables, we have:
(1 - P/K)(1 - T/P) dP = rp dt
Integrating both sides:
∫ (1 - P/K)(1 - T/P) dP = ∫ rp dt
Let's evaluate the integral on the left side:
∫ (1 - P/K)(1 - T/P) dP = ∫ (1 - P/K - T/K + T/(KP)) dP
= ∫ (1 - P/K) - (T/K) + (T/PK) dP
= P - (P^2)/(2K) - (T/K)P + (T/K)ln(P) + C1
On the right side, we have:
∫ rp dt = rt + C2
Combining both sides and simplifying, we have:
P - (P²2)/(2K) - (T/K)P + (T/K)ln(P) + C1 = rt + C2
To solve for the constants C1 and C2, we use the initial condition P(0) = P0:
P0 - (P0²2)/(2K) - (T/K)P0 + (T/K)ln(P0) + C1 = r(0) + C2
P0 - (P0²2)/(2K) - (T/K)P0 + (T/K)ln(P0) + C1 = C2
Substituting the given values:
15 - (15²2)/(2×100) - (10/100)×15 + (10/100)ln(15) + C1 = C2
15 - (225/200) - (150/100) + (10/100)ln(15) + C1 = C2
15 - 1.125 - 1.5 + 0.1ln(15) + C1 = C2
Simplifying further, we have:
12.375 + 0.1ln(15) + C1 = C2
Now we have the general solution:
P - (P²2)/(2K) - (T/K)P + (T/K)ln(P) = rt + C
Using the initial condition P(0) = 15, we can solve for C:
15 - (15²2)/(2×100) - (10/100)×15 + (10/100)ln(15) = r(0) + C
15 - 1.125 - 1.5 + 0.1ln(15) = C
11.375 + 0.1ln(15) = C
Therefore, the solution for the number of tigers present over time is given by:
P - (P²2)/(2K) - (T/K)P + (T/K)ln(P) = rt + 11.375 + 0.1ln(15)
This is the general solution for the population of Bengal tigers in the conservation park.
To know more about Equation related question visit:
https://brainly.com/question/29657983
#SPJ11
A rectangular birthday present, 3 in. by 7 in. by 8 in., is covered by wrapping paper. How much wrapping paper is required?
a.
146 sq. in.
b.
101 sq. in.
c.
202 sq. in.
d.
168 sq. in.
Answers
The amount of wrapping paper that is required is; c. 202 sq. in.
What is the surface area of the rectangular cuboid?The formula for the surface area of a rectangular cuboid is given as:
SA = 2(lw + lh + hw)
where;
l = length
h = height
w = width
We are given;
Length; l = 3 in.
Width; w = 7 in.
Height; h = 8 in.
Thus, surface area is;
SA = 2((3*7) + (3*8) + (8*7))
SA = 2(21 + 24 + 56)
SA = 2(101)
SA = 202 sq. in
Read more about surface area of the rectangular cuboid at; https://brainly.com/question/20919556
#SPJ1
1.35 divided by 3.8 repeating
Answers
Answer:
it is 0.34
Step-by-step explanation:
PLEASE HELP ME!
EXPLANATION = BRAINLIEST
the area is ___ square units

Answers
Answer:
50 units²
Step-by-step explanation:
Solve for both long sides:
6² + 8² = x²
36 + 64 = x²
100 = x²
x = 10
Solve for both short sides:
3² + 4² = x²
9 + 16 = x²
25 = x²
x = 5
Area:
5 x 10 = 50
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
Answer:
Step-by-step explanation:

A boat is heading towards a lighthouse, whose beacon-light is 113 feet above thewater. From point A, the boat's crew measures the angle of elevation to the beacon,10°, before they draw closer. They measure the angle of elevation a second time frompoint B at some later time to be 21°. Find the distance from point A to point B.Round your answer to the nearest foot if necessary.
Answers
The following picture represents an explanation to the given question:
CD represents the beacon
We need to find the distance AB
The measure of the angle C = 90
At the triangle BCD,
The measure of the angle CDB = 90 - 21 = 69
Using the sine law, we will find the length of BD
So,
\(\begin{gathered} \frac{BD}{\sin90}=\frac{CD}{\sin 21} \\ BD=CD\cdot\frac{\sin90}{\sin21}=\frac{CD}{\sin 21} \end{gathered}\)At the triangle ABC
The measure of the angle CDA = 90 - 10 = 80
So, the measure of the angle ADB = angle CDA - angle CDB = 80 - 69 = 11
At the triangle ADB, using sin law:
\(\begin{gathered} \frac{AB}{\sin D}=\frac{BD}{\sin A} \\ \\ AB=BD\cdot\frac{\sin D}{\sin A}=BD\cdot\frac{\sin 11}{\sin 10} \end{gathered}\)substitute with the value of BD and CD s
So,
\(AB=\frac{CD}{\sin21}\cdot\frac{\sin11}{\sin10}=\frac{113\cdot\sin 11}{\sin 21\cdot\sin 10}=346.4798\)Rounding the answer to the nearest foot
So, the answer will be AB = 346 ft

Find the distance from point B to point A.
Enter as a decimal rounded to the nearest tenth.
A
34°
608 m
B
BA = [?] m
C

Answers
Answer:
BA ≈ 410.1 m
Step-by-step explanation:
using the tangent ratio in the right triangle
tan34° = \(\frac{opposite}{adjacent}\) = \(\frac{BA}{BC}\) = \(\frac{BA}{608}\) ( multiply both sides by 608 )
608 × tan34° = BA , then
BA ≈ 410.1 m ( to the nearest tenth )
Find the UX
can someone help me rn, please ??!!

Answers
Answer:
The answer is 9x + 3
Step-by-step explanation:
Given;UV = 3x + 1VW = 4x – 6WX = 2x + 8To Find;UX = ?Now,
UX = UV + VW + WX
UX = (3x + 1) + (4x – 6) + (2x + 8)
UX = 3x + 1 + 4x – 6 + 2x + 8
UX = 3x + 4x + 2x + 1 – 6 + 8
UX = 9x + 3
Thus, The answer is 9x + 3
-TheUnknownScientist 72
The value of line segment UX is,
UX = 9x + 3
We have to given that,
UV = 3x + 1
VW = 4x – 6
WX = 2x + 8
Now, We can see by the image,
UX = UV + VW + WX
Substitute all the given values,
UX = (3x + 1) + (4x – 6) + (2x + 8)
UX = 3x + 1 + 4x – 6 + 2x + 8
UX = 3x + 4x + 2x + 1 – 6 + 8
UX = 9x + 3
Thus, The answer is, 9x + 3
Learn more aboput the line segment visit:
https://brainly.com/question/280216
#SPJ6
True or false: a local variable is a variable defined inside a function that can only be used inside its function
Answers
Given statement 'a local variable is a variable defined inside a function that can only be used inside its function' is False
A local variable is a type of variable that we declare inside a block or a function, unlike the global variable. They can be used only by the statements that are inside the function or the block of the code. Local variables are not known to functions outside their own.
The variable declared is local within that function that is the declared variable is accessible inside that block itself, it cannot be accessible outside the given function.
Consider the following multiplication function:
ex - void multi()
{
int a = 10, b = 2, c ;
c = a * b ;
cout << c ;
}
int main()
{
cout << "value for c is :"<< c ;
return 0;
}
Here inside the multi function variable a, b, c are declared and initialized inside the function.
Thus, a local variable is defined inside the body of the function and is not accessible outside of the function.
Therefore, given statement 'a local variable is a variable defined inside a function that can only be used inside its function' is False
Learn more about the local variable here:
brainly.com/question/27840441
#SPJ4
The recipe called for a ratio of sugar and flour to be 2 lbs to 9 lbs. If the chef used 18 lbs. of flour, how many pounds of sugar are needed?
Answers
Answer:
3/8 lb or 6 oz
Step-by-step explanation:
given the graph of the function f(x)=1/x2 write the equation g(x)
horizontal compression by 1/5
vertical stretch by a factor of 7
reflection in y-axis
translation 10 units left and 1 unit down
Answers
Answer:g(x)
Step-by-step explanation:1/5 g (x)
Please help! Will mark brainliest! :))))

Answers
Answer:
1. D
2. A
3. C
4. D
5. B
6. B
7. C
8. D
have a good day.
Is the coordinates of a point are 3 and 4?
Answers
The coordinates of the point at 3/4 of the distance from A to B from A is (-3.5, 1.25)
The coordinates of point A = (-5, -4),
The coordinates of the point B = (-3, 3)
Let the point at the distance 3/4 from A to B = P
The coordinates of point 3/4 from A to B = P
At the x-coordinate, the distance from B to A is = -3-(-5) = 2 units.
At the y-coordinate, the distance from B to A is = 3-(-4) = 7 units.
Hence, the coordinates of P = (-5 + (3/4×(x-coordinate), -4 + 3/4×(y-coordinate)
P = (-5 + (3/4×(2), -4 + 3/4×(7))
P = (-3.5, 1.25)
Hence, the coordinates of the point at 3/4 of the distance from A to B from A is (-3.5, 1.25).
Read more about the section formula :
brainly.com/question/14812336
#SPJ4
The complete question is -
What are the coordinates of the point 3/4 of the way from A to B?
