Find a linear equation of the line with a slope 3 passing through the point
(-9,7).
Answers
b=-9-21=-30
Equation: y=3x-30
Related Questions
A card is drawn from a standard deck of 52 cards. What is the probability of drawing a face card (jack, king, or queen) or a black card? (Hint: Half of a standard deck of 52 cards has black cards. )
Answers
To determine the probability of an event occurring, we divide the number of favorable outcomes by the total number of possible outcomes. the probability of drawing a face card or a black card is 35/52,
The probability of drawing a face card (jack, king, or queen) or a black card from a standard deck of 52 cards can be calculated as follows:
In a standard deck of 52 cards, there are 12 face cards (3 face cards each for jack, king, and queen) and 26 black cards (clubs and spades). However, 3 of the face cards (jack, king, queen) are also black. To avoid double-counting, we need to subtract these 3 cards from the total count of black cards.
Therefore, the number of favorable outcomes (face cards or black cards) is 12 + (26 - 3) = 35. The total number of possible outcomes is 52.
Hence, the probability of drawing a face card or a black card is 35/52, which simplifies to 5/7 or approximately 0.714.
To learn more about probability click here : brainly.com/question/32004014
#SPJ11
A circle with a diameter of 10 cm and a central angle of 30° is drawn below.
what is the area, to the nearest tenth of a square centimeter, of the sector formed by the 30° angle?
(A) 5.2 (B) 6.5 (C) 13.1 (D) 26.2

Answers
Answer:
B 6.5
Step-by-step explanation:
The area of a whole circle is
a = \(\pi\)\(r^{2}\) A whole circle is 360 degrees. We only have part of a circle. We were also given the diameter and we need the radius. The radius is half of the diameter.
a = \(\frac{30}{360} \pi 5^{2}\)
a= 6.5 rounded.
A whole circle exists 360 degrees. The radius exists half of the diameter.
\($$a = (30/360) $\pi 5^2\)
a = 6.5 rounded.
The area to the nearest tenth of a square centimeter, of the sector formed by the 30° angle exists at 6.5 rounded.
How to calculate the area of a circle with diameter?The diameter of the circle exists double the radius of the circle. Therefore the area of the circle formula utilizing the diameter exists equivalent to π/4 times the square of the diameter of the circle. The formula for the area of the circle, utilizing the diameter of the circle
π/4 × \($$diameter^2\).
Given: diameter of the circle = 10 cm
then the radius of the circle is half of the diameter
Radius of the circle = 10/2 = 5 cm
Area of circle = \($$\pi $r^2\)
Where r be the radius of the circle
A whole circle exists 360 degrees. The radius exists half of the diameter.
\($$a = (30/360) $\pi 5^2\)
simplifying the above equation we get
\($$a = 25$\pi$ /$12\)
a = 6.5 rounded.
The area to the nearest tenth of a square centimeter, of the sector formed by the 30° angle exists at 6.5 rounded.
Therefore, the correct answer is option (B) 6.5
To learn more about the area of the circle refer to:
https://brainly.com/question/14068861
#SPJ9
In a city of 26000 populations, 5000 read English newspaper, 12000 read Nepali newspaper and 1000 read both. What percentage read neither English and Nepali newspaper? ( from set theory )
Answers
Answer:
38.46%
Step-by-step explanation:
total readers=16000
population=26000
no of non-readers=total population-total readers
=26000-16000
=10000
percentage of non-readers=non-readers×100%
population
=10000×100%
26000
percentage of non-readers is 38.46%
please help I'm in summer school
Look at the graph. Cost of Toy Cars A graph with cars on the x-axis and cost on the y-axis. A line goes through points (0, 0), (2, 3), (4, 6). What is the cost of 18 toy cars? $12 $20 $22 $27
Answers
Answer:
i dont know
Step-by-step explanation:
i dont know
I´m gonna fail
Help
PLease and thank you

Answers
Answer:
Step-by-step explanation:
-8y-4x^3-1
Answer:
-1 - 8y - 4x³
or
-8y - 4x³ - 1
or
4x³ - 8y - 1
Step-by-step explanation:
7 - 6y - 5x³ - 1 + x³ - 7 - 2y
add LIKE terms
- 6y - 2y
7 - 1 - 7
-5x³ + x³
=
-1 - 8y - 4x³
Hope this helps and a thank won't hurt! :)
Can someone give me a step by step tut on how 135 divided by 20 is 6.75…I just forgot.
Answers
Answer: 135/20=6.75
Step-by-step explanation:
Long division (picture attached below)

4 boxes can hold 40 books how many books per box
Answers
Answer:
10 books per box
Step-by-step explanation:
40÷4
=10
10×4= 40
So there will be 10 books each 4 boxes
simple random sample of size n= 38 is obtained from a population with u = 67 and or 14. (a) What must be true regarding the distribution of the population in order to use the normal model to compute probabilities involving the sample mean? Assuming that this condition is true, describe the sampling distribution of x. (b) Assuming the normal model can be used, determine P(x< 70.4). (c) Assuming the normal model can be used, determine P(x 2 69.4). A simple random sample of size n= 38 is obtained from a population with u = 67 and or 14. (a) What must be true regarding the distribution of the population in order to use the normal model to compute probabilities involving the sample mean? Assuming that this condition is true, describe the sampling distribution of x. (b) Assuming the normal model can be used, determine P(x< 70.4). (c) Assuming the normal model can be used, determine P(x 2 69.4).
Answers
(a) In order to use the normal model to compute probabilities involving the sample mean, the distribution of the population must be approximately normal or the sample size must be sufficiently large (typically n ≥ 30). This condition is necessary because the sampling distribution of the sample mean approaches a normal distribution as the sample size increases, regardless of the shape of the population distribution.
The sampling distribution of the sample mean, denoted by X, is the distribution of all possible sample means that could be obtained from repeated random sampling. If the population distribution is approximately normal or the sample size is large, the sampling distribution of X will be approximately normal, regardless of the shape of the population distribution. The mean of the sampling distribution is equal to the population mean (µ), and the standard deviation is equal to the population standard deviation divided by the square root of the sample size (σ/√n).
(b) Assuming the normal model can be used, to determine P(x < 70.4), we need to calculate the z-score corresponding to the sample mean x = 70.4 and then find the probability associated with that z-score. The formula for the z-score is given by:
z = (x - µ) / (σ/√n)
where x is the sample mean, µ is the population mean, σ is the population standard deviation, and n is the sample size.
In this case, x = 70.4, µ = 67, σ = 14, and n = 38. Plugging these values into the formula, we get:
z = (70.4 - 67) / (14/√38) ≈ 1.336
To find the probability P(x < 70.4), we need to find the area under the standard normal curve to the left of the z-score of 1.336. This can be looked up in the standard normal distribution table or calculated using statistical software. Let's assume the probability is approximately 0.909 (rounded to three decimal places).
Therefore, P(x < 70.4) ≈ 0.909.
(c) Similarly, to determine P(x ≥ 69.4), we need to find the probability associated with the z-score corresponding to x = 69.4. The z-score is calculated using the same formula as in part (b):
z = (x - µ) / (σ/√n)
Plugging in the values, we have:
z = (69.4 - 67) / (14/√38) ≈ 0.641
To find P(x ≥ 69.4), we need to find the area under the standard normal curve to the right of the z-score of 0.641. Let's assume the probability is approximately 0.737 (rounded to three decimal places).
Therefore, P(x ≥ 69.4) ≈ 0.737.
To know more about Probability visit-
brainly.com/question/31828911
#SPJ11
A school is building a rectangular stage for its chorus. The stage must have a width of 8 feet. The area of the stage must be more than 96 square feet. (The stage must hold all the singers.) Write an inequality that describes the possible lengths (in feet) of the stage. Use l for the length of the rectangular stage.
Answers
Answer:
Step-by-step explanation:
Answer: Length ≥ 6 feet
Step-by-step explanation:
The area of a rectangle= length × width
In this case, the width is 4 feet and the area of the stage must be at most 24 square feet.
The inequality that describes the possible lengths (in feet) of the stage would be:
Length × Width ≥ 24
Length × 4 ≥ 24
Length ≥ 24/4
Length ≥ 6
Therefore, the length must be at most 6 feet.
Show that y, = x3 is a solution to the differential equation xy" - 5xy' +9y=0 b. Find a second independent solution, yz, to the differential equation x2y" - 5xy' +9y=0.
Answers
The given differential equation n is xy" - 5xy' + 9y = 0. To show that \(y = x^3\)is a solution to this equation, we substitute y =\(x^3\)into the differential equation and demonstrate that it satisfies the equation.
a. To show that y = x^3 is a solution to the differential equation xy" - 5xy' + 9y = 0, we substitute y = x^3 into the equation:
\(x(x^3)'' - 5x(x^3)' + 9(x^3) = 0\)
Taking derivatives:
\(x(6x - 10) - 5x(3x^2) + 9x^3 = 0\)
\(6x^2 - 10x - 15x^3 + 9x^3 = 0\)
\(-6x^2 - x + 9x^3 = 0\)
Simplifying the equation:
\(9x^3 - 6x^2 - x = 0\)
The equation holds true, which confirms that \(y = x^3\) is a solution to the given differential equation.
b. To find a second independent solution, we use the method of reduction of order. Let y = v(x)y1(x), where y1(x) = x^3 is the known solution. Substituting this into the differential equation, we have:
\(x^2v''(x)y1(x) + x^2v'(x)y1'(x) - 5xv'(x)y1(x) + 9v(x)y1(x) = 0\)
Simplifying the equation and substituting y1(x) = x^3:
\(x^2v''(x)x^3 + x^2v'(x)3x^2 - 5xv'(x)x^3 + 9v(x)x^3 = 0\)
\(x^5v''(x) + 3x^4v'(x) - 5x^4v'(x) + 9x^3v(x) = 0\)
\(x^5v''(x) - 2x^4v'(x) + 9x^3v(x) = 0\)
Next, we can simplify further and divide the equation by x^3:
\(x^2v''(x) - 2xv'(x) + 9v(x) = 0\)
This is a second-order linear homogeneous differential equation, which can be solved using various methods, such as the method of undetermined coefficients or the method of variation of parameters. Solving this equation will provide us with a second independent solution, y2(x), to the original differential equation\(x^2y" - 5xy' + 9y = 0.\)
Learn more about derivatives here:
https://brainly.com/question/25324584
#SPJ11
3- if we know that a patient received the antidepressant (desipramine), what is the probability that they relapsed?
Answers
The probability that a patient will relapse after receiving desipramine depends on a variety of factors, such as dosage, duration of treatment, and pre-existing mental health conditions.
Generally speaking, it is estimated that around 50-70% of people who take desipramine as an antidepressant will experience relapse within six months of treatment cessation.
However, this rate can be decreased through longer treatment periods and/or higher doses of medication.
Additionally, patients may also benefit from lifestyle changes, such as increased physical activity, increased social engagement, and improved dietary habits.
Taking all of these factors into consideration, it is difficult to determine the exact probability of relapse in any given case.
To know more about antidepressant click on below link:
https://brainly.com/question/14307922#
#SPJ11
PLS HELP I BEG U!!!!!!!!!!!!

Answers
Answer: Number six should be 14/18.
Step-by-step explanation:
The simplified answer is 7/9.
In this graph the y-intercept of the line is (Blank). The equation of the line is y=(Blank) x (Blank) .

Answers
The equation of the line is y = x - 2.
What is a Line??
A line can be defined by a shortest distance between two points is called as a line.
According to the graph we negative intercept at x =0, y = -2 and two points (0,-2) and (2,0).
Equation can be given as.
y = mx + c
c = -2
m = 0- (-2)/ 2- 0
m = 1
y = x - 2
Thus, the equation of the line is y = x - 2.
Learn more about lines here:
brainly.com/question/2696693
#SPJ2
find the area of this triangle

Answers
Work Shown:
area = 0.5*base*height
area = 0.5*11*13.4
area = 73.7 square cm
The other values 15 and 14 are not used. Your teacher probably put them in as a distraction.
The same report from the u.s. census bureau states that in 2010 the average commute time for wake county workers was 23.9 minutes and in 2016 the average was 25 minutes. what was the percentage increase in average commute times between these years? write your answer as a percentage rounded to two decimal places, but do not include the % symbol.
Answers
The percentage increase in average commute times between these years = 2.25%
Calculation of percentage increaseIn 2010, the average commute time for wake county workers = 23.9 mins
In 2016, the average commute time for wake county workers = 25 mins.
The increase is = 25- 23.9 = 1.1
The average commute time between the two years,
23.9+25 = 48.9 mins
Therefore, the percentage,
= 1.1/48.9×100
= 110/48.9
= 2.249%
= 2.25% to the nearest two decimal places.
Learn more about percentage here:
https://brainly.com/question/24877689
#SPJ4
How do you calculate raw data?
Answers
Raw data can be calculated by using mathematical operations such as addition, subtraction, multiplication, and division.
This can be done manually or by using a calculator or a computer program .Additionally, statistical methods such as mean, median, mode, and standard deviation can be used to calculate raw data.Raw data can also be manipulated in various ways. For example, data can be sorted, filtered, and organized into categories or hierarchies. Data can also be visualized in graphs, charts, and diagrams to make patterns and trends easier to identify. Statistical methods such as correlation and regression can also be used to analyze and interpret raw data. Additionally, data can be combined with other data sets to create new insights and relationships. Finally, machine learning and predictive analytics can be used to make predictions about future outcomes based on existing data.
Learn more about raw score here
https://brainly.com/question/29022735
#SPJ4
Which ordered pair is the best estimate for the solution to the system?

Answers
The ordered pair that is the best estimate for the solution to the system is (0.5, -3.5)
Ordered Pair:
An ordered pair refers to a set of two numbers used to locate a point in a coordinate plane. Here the first point refers the x - coordinate and the second value represents the y - coordinate.
Given,
Her we have the equations,
3x - 8y = 29
3x + y = -2
Now, we need to find the solution of the system.
Here we have to use the substitution method in order to solve this one.
For that, we have to rewrite the second equation as,
y = -2 - 3x.
Now, we have to apply the value of y on the equation (1), then we get,
3x - 8(-2 - 3x) = 29
3x + 16 + 24x = 29
27x = 29 - 16
27x = 13
x = 13/27
x = 0.5
When we apply the value of x into the equation, then we get the value of y as,
y = -2 - 3(0.5)
y = -2 - 1.5
y = -3.5
Therefore, the solution of the system is (0.5, - 3.5).
To know more about Ordered pair here.
https://brainly.com/question/28874341
#SPJ1
please help!
Given YZ tangent to ⊙J at point Y and m∠WYZ = 104, what is mWXY?

Answers
The measure of the angle WXY is 152 degrees
Calculating the measure of the angle WXY?From the question, we have the following parameters that can be used in our computation:
Line segment YZ tangent to J at point Y The measure of m∠WYZ = 104,Using the above as a guide, we have the following:
m∠MYW = 104 - 90
m∠MYW = 14
The inscribed angle opposite to the same arc is half of the external angle
So, we have
mw = 2 * m∠MYW
mw = 2 * 14
mw = 28 degrees
Also, we have
my = 180 degrees
So, we have
Angle WXY = 180 - 28
Evaluate the difference
Angle WXY = 152
Hence, the measure of the angle is 152 degrees
Read more about angles at
https://brainly.com/question/98924
#SPJ1
Assume that the helium porosity of coal samples taken from any particular seam is Normally distributedwith true standard deviation 0.75.a. Compute a 95% CI for the true average porosity of a certain seam if the average porosity for 20specimens from the seam was 4.85.b. Compute a 98% CI for true average porosity of another seam based on 16 specimens with asample average of 4.56.c. How large a sample size is necessary if the width of the 95% interval is to be 0.40?d. What sample size is necessary to estimate the true average porosity to within 0.2 with 99%confidence?
Answers
a. We are 95% confident that the true average porosity of the seam is between 4.25 and 5.45.
b. We are 98% confident that the true average porosity of the seam is between 3.68 and 5.44.
c. A sample size of at least 14 is necessary.
d. A sample size of at least 138 is necessary.
a. To compute a 95% confidence interval for the true average porosity of a certain seam, we use the formula:
CI = x ± tα/2 (s/√n)
where x is the sample average porosity, s is the sample standard deviation, n is the sample size, and tα/2 is the t-value with n-1 degrees of freedom and α/2 probability (0.025 for a 95% confidence interval).
Substituting the given values, we get:
CI = 4.85 ± 2.093 (0.75/√20)
= (4.25, 5.45)
Therefore, we are 95% confident that the true average porosity of the seam is between 4.25 and 5.45.
b. To compute a 98% confidence interval for the true average porosity of another seam, we use the same formula as in part (a), but with a different t-value (2.602 for a 98% confidence interval).
Substituting the given values, we get:
CI = 4.56 ± 2.602 (0.75/√16)
= (3.68, 5.44)
Therefore, we are 98% confident that the true average porosity of the seam is between 3.68 and 5.44.
c. To find the necessary sample size for a 95% confidence interval with a width of 0.40, we use the formula:
n = (tα/2 (s/width))^2
Substituting the given values and solving for n, we get:
n = (1.96 (0.75/0.40))^2
= 13.55
Therefore, a sample size of at least 14 is necessary.
d. To find the necessary sample size for a 99% confidence interval with a width of 0.2, we use the same formula as in part (c), but with a different t-value (2.576 for a 99% confidence interval).
Substituting the given values and solving for n, we get:
n = (2.576 (0.75/0.2))^2
= 137.68
Therefore, a sample size of at least 138 is necessary.
Learn more about confidence interval at https://brainly.com/question/16008484
#SPJ11
A measuring Task objective => To investigate your local athletics track to see wheather it is worked fairly for runners. who start on different lines.
Answers
The Task objective chosen is: A Measuring Task
The Objective is: To investigate the fairness of a local athlete's track for runners starting on different lines.
How do one carry about the investigation about?To carry about the investigation, follow the steps given below.
Choose a nearby sportsman's racetrack that you wish to examine.Split the pathway into several lanes, with a minimum of three lanes.Determine the length of each lane by utilizing either a measuring tape or measuring wheel. Make sure the measurements are precise.Place cones or markers to designate the starting points for each lane.Request the presence of a cohort of individuals who engage in running to take part in the study.Record the duration of each runner in completing the track for every lane.Evaluate the outcomes and contrast the timings of athletes beginning from distinct tracks.Closely examine the time variances among distinct lanes.Draw inferences from the examination. Inconsistent differences in lane times may indicate an unfair advantage for certain runners depending on their starting position.Lastly, make a crossword puzzle that includes mathematical vocabulary in a clever manner.
Learn more about investigation from
https://brainly.com/question/28158885
#SPJ1
```Class IX```
*Mathematics Project work*
*Do any one*
1. *A Measuring Task*
To investigate your local athletes track to see whether it is worked fairly for runners who start on different lines.
2. *Design a crossword puzzle with mathematical terms*
To review mathematics vocabulary, to give the opportunity for creative expression in designing puzzles, to act as a means of motivating the study of a given unit and to given recreation .
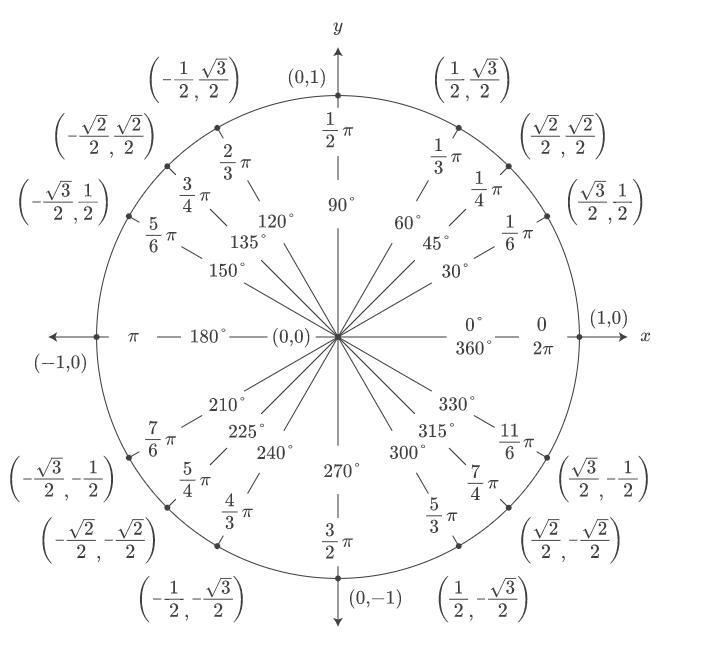
The measure of angle t is 60 degrees. What is the x-coordinate of the point where the terminal side intersects the unit circle? One-half StartFraction StartRoot 2 EndRoot Over 2 EndFraction StartFraction StartRoot 3 EndRoot OVer 2 EndFraction
Answers
Answer:
(a) 1/2
Step-by-step explanation:
The coordinates of the point of intersection of the terminal side of angle α with the unit circle are ...
(x, y) = (cos(α), sin(α))
When α = 60°, the x-coordinate of the terminal point is cos(60°) = 1/2.
For a certain relationship, y varies inversely with x. When x is 4, y is equal to 30. What is the value of y when x is equal to 10?
Answers
Step-by-step explanation:
inversely means
y = k/x
therefore
30 = k/4
120 = k
y = 120/10 = 12
FYI :
directly would mean
y = kx
The value of y will be 12 when x is equal to 10.
What is inverse variation?The relationship between two variables known as "inverse variation" occurs when the value of one variable increases while the value of the other variable decreases.
Given that, y varies inversely with x.
Here, y∝1/x
y=k/x
xy=k
When x is 4, y is equal to 30, we get
k=4×30
k=120
When x=10, we get
10y=120
y=12
Therefore, the value of y will be 12 when x is equal to 10.
Learn more about the inverse variation here:
brainly.com/question/11592410.
#SPJ2
help it is due in 10 mins

Answers
Answer:
independent- hours
dependent- money earned
the amount of money you make depends on the amount of hours you babysit
y=8x
Step-by-step explanation:
Image attached with 30 points :).
express x^2 + 4x - 7 in the form....

Answers
Answer:
Hope that helps
Step-by-step explanation:

What is the solution to the pair of simultaneous equations? 2x+y=5. 3x-2y=4
Answers
Answer:
(2, 1)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightDistributive Property
Equality Properties
Multiplication Property of Equality Division Property of Equality Addition Property of Equality Subtraction Property of EqualityAlgebra I
Coordinates (x, y)Terms/CoefficientsSolving systems of equations using substitution/eliminationStep-by-step explanation:
Step 1: Define Systems
2x + y = 5
3x - 2y = 4
Step 2: Rewrite Systems
Manipulate 1st equation
[Subtraction Property of Equality] Subtract 2x on both sides: y = 5 - 2xStep 3: Solve for x
Substitution
Substitute in y [2nd Equation]: 3x - 2(5 - 2x) = 4[Distributive Property] Distribute -2: 3x - 10 + 4x = 4[Addition] Combine like terms: 7x - 10 = 4[Addition Property of Equality] Add 10 on both sides: 7x = 14[Division Property of Equality] Divide 7 on both sides: x = 2Step 4: Solve for y
Substitute in x [Modified 1st Equation]: y = 5 - 2(2)Multiply: y = 5 - 4Subtract: y = 1On Dec. 10, Merchandise is sold for $2,0002/10, n/30 to ABC who sends a remittance on Dec. 26 . What is the amount of remittance? a. 1,800 b. 1,400 c. 1,960 d. 2,000
Answers
The amount of the remittance from ABC is $1,960.
The given information states that merchandise is sold for $2,000 with terms of 2/10, n/30 to ABC. The terms 2/10, n/30 imply a 2% discount if payment is made within 10 days, with the full amount due within 30 days.
Since ABC sends a remittance on Dec. 26, it means the payment is made after the discount period but within the credit period. Therefore, ABC is not eligible for the discount of 2%.
To calculate the amount of the remittance, we simply subtract the discount from the total amount. In this case, the discount is $2,000 * 2% = $40. Thus, the remittance amount is $2,000 - $40 = $1,960.
In conclusion, the amount of the remittance from ABC is $1,960, as they did not qualify for the early payment discount.
Learn more about credit periods here:
brainly.com/question/2264363
#SPJ11
The random variable, number of customers entering a store between 9am and noon, is an example of a discrete random variable.(True/false)
Answers
The statement, "number of customers entering a store between "9am" and noon, is an example of a discrete-random-variable." is True because the number of customers are finite.
The "random-variable" "number of customers entering the store between 9am and noon" is considered as an example of a discrete random variable.
A "discrete" random variable is defined as a variable that can take on only a finite or countable number of values, where the values are usually integers.
In this case, the number of customers entering a store can only take on integer values (0, 1, 2, 3, etc.), and there is a finite limit to the number of customers who could potentially enter the store during that time period.
Therefore, the statement is True.
Learn more about Random Variable here
https://brainly.com/question/30066447
#SPJ4
two cards are selected in a sequence from a standard deck. what is the probability that the second card is a jack given that the first card was a 2. (assume the 2 was not replaced.)
Answers
The probability that the second card is a jack given that the first card was a 2 is 52/51.
To calculate the probability that the second card is a jack given that the first card was a 2, we need to consider the remaining cards in the deck after the first card is drawn.
When the first card is drawn and it is a 2, there are 51 cards remaining in the deck, out of which there are 4 jacks.
The probability of drawing a jack as the second card, given that the first card was a 2, can be calculated using conditional probability:
P(Second card is a jack | First card is a 2) = P(Second card is a jack and First card is a 2) / P(First card is a 2)
Since the first card is already known to be a 2, the probability of the second card being a jack and the first card being a 2 is simply the probability of drawing a jack from the remaining 51 cards, which is 4/51.
The probability of the first card being a 2 is simply the probability of drawing a 2 from the initial deck, which is 4/52.
P(Second card is a jack | First card is a 2) = (4/51) / (4/52)
Simplifying the expression:
P(Second card is a jack | First card is a 2) = (4/51) * (52/4)
P(Second card is a jack | First card is a 2) = 52/51
To learn more about probability click here:
brainly.com/question/30736116
#SPJ11
Distribute:
-3x(7x-2)
Answers
-21x + 6x (i'm pretty sure)
A= (a, b} B = {1,2,3} Select the expression that is an element of AxBxB. O (1,2,3) (a, a,1) (,22 (2.1.1)
Answers
The expression that has the element of A*B*B is Option A - (b,2,3)
Sets are groups of clearly defined objects or elements in mathematics. A set is denoted by a capital letter, and the cardinal number of a set is enclosed in a curly bracket to indicate how many members there are in a finite set.
The "elements" of a set are the objects that make up the collection. Sets are equal if and only if they have the same elements, therefore a = A denotes that 'a' is one of A's elements. For sets, repetition and order are irrelevant.
Given, A={a.b} and B=[1,2,3]
Since the required expression was supposed to have the element of A*B*B the correct option would be A since it has elements b from A, 2 from B, and 3 from B, fulfilling all the required elements.
To learn more about discrete maths visit: brainly.com/question/27793609
#SPJ4