What is the distance between (2, 5) and (2,-5) on the coordinate plane
Answers
Answer:
10
Step-by-step explanation:
When you find the distance, you just add both of the numbers as if they were in absolute value 5+|-5|
so then since the x values are the same, you would go up/down 10 spaces on the Y-axis
Answer:
10 units
Step-by-step explanation:
Use the distance formula:
\(\sqrt{ (x_{2} - x_{1} )^2 -(y_{2} - y_{1} )^2\)
Plug in values:
\(\sqrt{ (-5-5 )^2 -(2-2 )^2\)
\(\sqrt 100\)
=10 units
Related Questions
a college professor conducted a survey in order to assess how much money nursing majors spend on course material compared to all other majors. to do so, she selected a random sample of 34 students. each student was classified as a nursing major or as a non-nursing major. they were then asked how much they spent on books and other materials required for their courses this semester. here are parallel boxplots summarizing the responses.
Answers
Option D. The median cost of course materials for nursing majors is over $300 more than the median cost of course materials for non-nursing majors.
The given boxplots show the circulation of the expense obviously materials for nursing majors and non-nursing majors. From the plots, we can reason that the scope of the circulation of the expense obviously materials for nursing majors is like that of non-nursing majors, as the most extreme and least qualities are around at a similar level. We can likewise infer that the most extreme expense for non-nursing majors is more prominent than the middle expense for nursing majors.
Also, the inconstancy of the expense obviously materials for the center half of nursing majors is more noteworthy than the fluctuation of the center half for non-nursing majors, as the cases for nursing majors are more extensive. In any case, we can't reason that the middle expense obviously materials for nursing majors is more than $300 more than the middle expense obviously materials for non-nursing majors, as the medians are not straightforwardly named and their division isn't plainly shown. At last, we can see that the study included 17 nursing majors and 17 non-nursing majors.
To learn more about statistics and data analysis, refer:
https://brainly.com/question/18351121
#SPJ4
The complete question is:
A college professor conducted a survey in order to assess how much money nursing majors spend on course material compared to all other majors. To do so, she selected a random sample of 34 students. Each student was classified as a nursing major or as a non-nursing major. They were then asked how much they spent on books and other materials required for their courses this semester. Shown above are parallel boxplots summarizing the responses. Based upon the boxplots, which of the following statements cannot be concluded?
A. The range of the distribution of the cost of course materials for nursing majors is about the same as that of non-nursing majors.
B. The maximum cost for non-nursing majors is greater than the median cost for nursing majors.
C. The variability of the cost of course materials for the middle 50% of nursing majors is greater than the variability of the middle 50% for non-nursing majors.
D. The median cost of course materials for nursing majors is over $300 more than the median cost of course materials for non-nursing majors.
E. The boxplots reveal that 17 students are nursing majors and 17 students are non-nursing majors
Michelle wants to start a babysitting club and decides to call a meeting. As a thank you to everyone for coming she decides to order pizza. She orders two large pepperoni and two extra-large cheese pizzas and the total comes to $30.00. When the delivery person arrives she hands him a $50.00 bill. How much change should she get back? If she tipped the delivery person 10% how much would she get back?
Answers
Answer:
I am not sure if my math is correct but I got $15 dollars in change.
Step-by-step explanation:
$50 times 0.10 (10%) equals $5. $50.00 minus $30.00 is $20.00. $20 minus $5 is $15.
A glider begins its flight 4/5 mile above the ground. After 30 minutes, it is 3/10 mile above the ground. Find the change in heigh of the glider. If it continues to descend at this rate, how long does the entire descent last?
Answers
Answer:1 hour 15 Minutes
Step-by-step explanation:The glider begins its flight mile above the ground.
Distance above the ground after 45 minutes =
Change in height of the glider
Next, we determine how long the entire descent last.
Expressing the distance moved as a ratio of time taken
Therefore: Total Time taken =45+30=75 Minutes
=1 hour 15 Minutes
2x+y-z=8
x+z=-5
2y-3z=21
Answers
Answer:
z=-5; x=0 ; y=3
Step-by-step explanation:
2x= -2z -10; -2z-10+y-z=8; y-3z-10=8; y-3z=18
2y-3z=21; 2y=3z+21; y= 1.5z+10.5; y-3z=18
1.5z+10.5-3z=18; -1.5z+10.5=18; -1.5z=7.5; z=-5
x+z=-5; x-5=-5; x=0; 2y-3z=21; 2y+15=21; 2y=6; y=3
2x+y-z=8; 2(0)+3-(-5)=8; 3+5=8; 8=8
6. Which characteristics correctly describe a proton? a) approximate mass 1 amu; charge +1; inside nucleus b) approximate mass 5 x 104 amu; charge -1; outside nucleus c) aproximate mass 5 x 104 amu; charge +1; inside nucleus d) approximate mass 1 amu; charge 0; inside nucleus e) approximate mass 1 amu; charge +1; outside nucleus
Answers
The correct characteristic that describes a proton is: a) approximate mass 1 amu; charge +1; inside nucleus.
A proton is a subatomic particle with a positive charge and a mass of approximately 1 atomic mass unit (amu). It is located inside the nucleus of an atom. Protons are fundamental particles found in all atomic nuclei and play a crucial role in determining the atomic number and identity of an element. Their positive charge balances the negative charge of electrons, creating a neutral atom.
To know more about nucleus,
https://brainly.com/question/25663043
#SPJ11
In the figure below, m || k. Find the values of x and z.
850
|(52 - 75)°
Z =
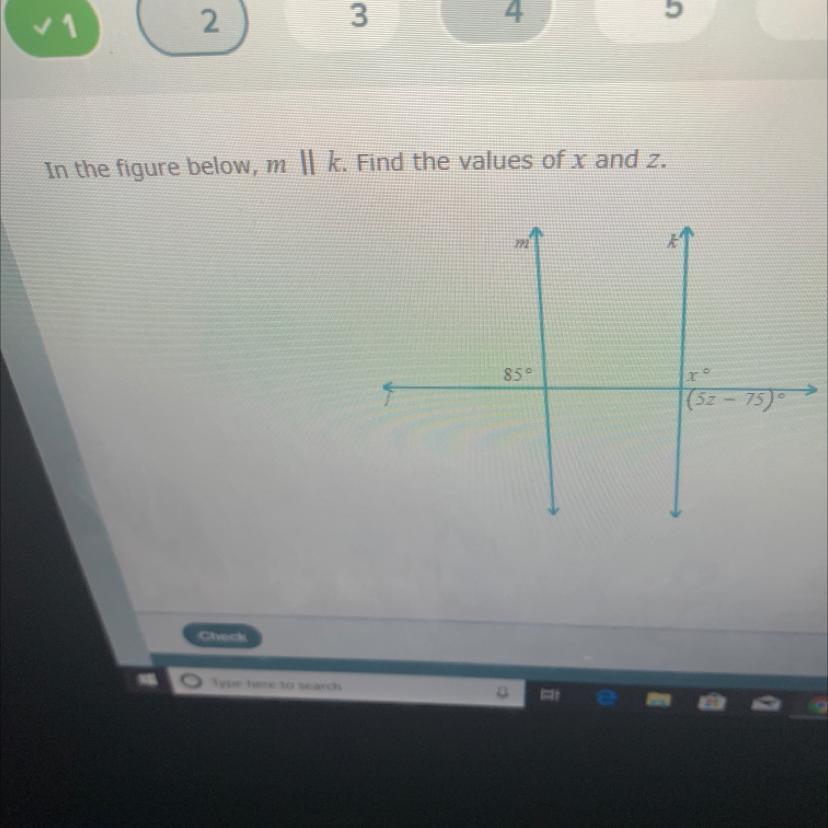
Answers
Answer:
z=33 x=90
Step-by-step explanation:
33 X 5 = 165 - 75 = 90 degress and x is a right angle so x is 90 degrees
Suppose the cumulative distribution function of the random variable X is F(x) = 0 when x<-2 , F(x) = .25x + .5 when -2 <= x < 2 and F(x) = 1 when 2<=x (<= means greater than or equal). Determine the following a. P(X<1.8) b. P(X>-1.5) c. P(X<-2) d. P(-1
Answers
the probability P(X<-2), we use the cumulative distribution function F(x) = 0 for x < -2. We plug in -2 for x in the function to get F(-2) = 0.
a. P(X<1.8) = .25(1.8) + .5 = .95
b. P(X>-1.5) = .25(-1.5) + .5 = .375
c. P(X<-2) = 0
d. P(-1.5<X<2) = .25(2) + .5 - (.25(-1.5) + .5) = .875
a. For the probability P(X<1.8), we use the cumulative distribution function F(x) = 0.25x + 0.5 for -2 <= x < 2. We plug in 1.8 for x in the function to get F(1.8) = 0.25(1.8) + 0.5 = 0.95. Therefore, P(X<1.8) = 0.95.
b. For the probability P(X>-1.5), we use the cumulative distribution function F(x) = 0.25x + 0.5 for -2 <= x < 2. We plug in -1.5 for x in the function to get F(-1.5) = 0.25(-1.5) + 0.5 = 0.375. Therefore, P(X>-1.5) = 0.375.
c. For the probability P(X<-2), we use the cumulative distribution function F(x) = 0 for x < -2. We plug in -2 for x in the function to get F(-2) = 0. Therefore, P(X<-2) = 0.
d. For the probability P(-1.5<X<2), we use the cumulative distribution function F(x) = 0.25x + 0.5 for -2 <= x < 2. We plug in -1.5 and 2 for x in the function to get F(-1.5) = 0.25(-1.5) + 0.5 = 0.375 and F(2) = 0.25(2) + 0.5 = 0.95. Therefore, P(-1.5<X<2) = 0.95 - 0.375 = 0.875.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
A 3-mi cab ride cost $7.90. A 9-mi cab ride cost $18.70
Answers
Answer:
first part: y=2.63x
second part: y=2.08x
Step-by-step explanation:
1) 7.90 / 3 = 2.633333 (I rounded to 2.63)
2) 18.70 / 9 = 2.07777 (I rounded to 2.08)
I hope this what you were asking
The cab ride for the 3.8 mile trip is $8.4 .
What is the slope of a straight line?Slope tells how vertical a line is.
The more the slope is, the more the line is vertical. When slope is zero, the line is horizontal.
To find the slope, we take the ratio of how much the line's height increases as we go forward or backward on the horizontal axis.
the points are (3, 7.90) and (9, 18.70)
y = mx + b
m = y2-y1/x2-x1
m = (18.70 - 7.90)/(9-3)
m = 10.8/6
m = 1.8
y = 1.8x + b
Put the values of x and y to find b ;
y = 1.8x + b
18.70 = 1.8(9) + b
10.5=8.75 + b
b=1.75
The equation of the line is y = 1.8x + 1.75
y=(1.8 X 3.8) + 1.75
y=6.65+1.75
y=8.4
Thus, The cab ride for the 3.8 mile trip is $8.4 .
The complete question is
A 3-mi cab ride cost $7.90. A 9-mi cab ride cost $18.70. How much does a 3.8-mi cab ride cost?
Learn more about slope here:
https://brainly.com/question/2503591
#SPJ2
In a large city, 70% of people own a cell phone. A sociologist wishes to study the impact cell phones have on society. To get started, the sociologist randomly samples 45 people in the city. Use a calculator to find the probability that of those 45 people sampled, between 33 and 36 of them own a cell phone
Answers
The probability that of those 45 people sampled, between 33 and 36 of them own a cell phone is 0.2413
How to solve for the probabilityWe have to solve for the probability that of those 45 people sampled, between 33 and 36 of them own a cell phone
The standard deviation is given as
\(s = \sqrt{} \frac{P(1-p)}{n}\)
where we have p = proportion = 70% = 0.7
q = 1 - p
= 1 - 0.7
= 30 % = 0.3
s = \(\sqrt{\frac{0.7(1-0.7}{45} }\)
= 0.07
we are to find the interval of
P(33 ≤ x ≤ 36)
this would be written as
(33 / 45 - 0.70) / 0.07 < z < (36 / 45 - 0.70) / 0.07)
p(0.49 < z < 1.46)
we have to find the critical values of p(z < 0.49) and p(z < 1.46)
= 0.9284 - 0.68721
= 0.2413
Read more on probability here: https://brainly.com/question/24756209
#SPJ1
Describe the possible lengths of the third side of the triangle given that the lengths of the other two sides are 2 feet and 40 inches.
Answers
The triangle's third side is between 1.333 and 5.333 feet long.
How to find the range for the third side of the Triangle?One that assumes the longer value supplied is the longest side in the triangle and one that assumes the third side is the longest side in the triangle to determine a range of values for the third side when given two lengths. For the solution, combine the two inequality's.
Given:
Two sides are 2 feet and 40 inches (3.33 ft)
Now, the range for the third side can be
2+ 3.333 = 5.333 feet
and, 3.333 - 2= 1.333 feet
Hence, the third side of the triangle lies between 1.333 feet and 5.333 feet.
Learn more about Triangle Inequality here:
https://brainly.com/question/1163433
#SPJ1
A city's population has increased 40% in the last 5 years and is now 53,782 people.
What was the population 5 years ago?
Answers
Given:
A city's population has increased 40% in the last 5 years and is now 53,782 people.
To find:
The population 5 years ago.
Solution:
Let x be the population 5 years ago.
A city's population has increased 40% in the last 5 years.
So, present population is
\(x+x\times \dfrac{40}{100}=x+0.4x=1.4x\)
It is given that the present population is 53782.
\(1.4x=53782\)
\(x=\dfrac{53782}{1.4}\)
\(x=38415.7142857\)
\(x\approx 38416\)
Therefore, the population 5 years ago was about 38416.
Write an algebraic expression for each verbal expression.
1) Nine plus the product of two and the number d.
Answers
Answer:
9 + 2nd
Step-by-step explanation:
I just did it
what are the missing numbers?

Answers
6Q = 30
14Q= 70
Answer:
5, 30, and 70
Step-by-step explanation:
Multiply by number of quarters by 5 to get the number of nickels.
find atleast 3 solutions for the following linear equation in two variables:2x + 3y = 4
Answers
First solution :
Say, x = 0
→ 2x + 3y = 4
→ 2(0) + 3y = 4
→ 0 + 3y = 4
→ 3y = 4
→ y = 4/3
x = 0, y = 4/3Second solution :
Say, x = 1
→ 2x + 3y = 4
→ 2(1) + 3y = 4
→ 2 + 3y = 4
→ 3y = 4 - 2
→ 3y = 2
→ y = 2/3
x = 1, y = 2/3Third solution :
Say, x = 2
→ 2x + 3y = 4
→ 2(2) + 3y = 4
→ 4 + 3y = 4
→ 3y = 4 - 4
→ 3y = 0
→ y = 0 ÷ 3
→ y = 0
x = 2, y = 0Q9 i. Comment whether the sequence is Converges or diverges. Obtain the first five terms of that sequence. ii. 2(1 + 3 (2+ 3 2 3 1 + 3 p (n + p) (n + 2p) (n2 + p) 4 + 3
Answers
i) The sequence is Converges.
ii) The first five terms of that sequence is 81.5
In this case, we do not have a geometric or arithmetic sequence, so we cannot use those techniques. However, we can use the comparison test or the ratio test. The comparison test states that if there exists a sequence that converges and is greater than or equal to the given sequence, then the given sequence converges. The ratio test states that if the limit of the absolute value of the ratio of consecutive terms of the sequence is less than 1, then the sequence converges.
Unfortunately, the given sequence is too complex to find a sequence that converges and is greater than or equal to the given sequence. Also, the ratio test is inconclusive since the limit of the absolute value of the ratio of consecutive terms is not easy to find.
Therefore, we cannot determine the convergence or divergence of the given sequence with the methods mentioned above. However, we can still find the first five terms of the sequence by plugging in values for n and p. For example, if we let n = 1 and p = 2, we get:
2(1 + 3(2+ 3² + 1 + 3(1+2)(1+4)(1²+2)/4 + 3...)
= 2(1 + 3(2+9+1+3(3)(5)(3)/4 + 3...)
= 2(1 + 3(12.75 + 3...)
= 81.5
Similarly, we can find the first five terms by plugging in different values for n and p.
To know more about convergence here
https://brainly.com/question/15415793
#SPJ4
What is 2/3 of a triangle?
Answers
According to the centroid theorem, the distance between the vertex and the midpoint of the sides equals 2/3 of a triangle's centroid.
The center of the object is known as the centroid. The centroid of a triangle is the location where the three medians of the triangle meet. The intersection of all three medians is another way to define it. The middle is a line that joins the midpoint of a side and the contrary vertex of the triangle. The ratio of the distance between the median and the centroid of the triangle is 2: 1. It can be determined by taking the average of all the triangle's vertices' x- and y-coordinate points.
Know more about centroid here: https://brainly.com/question/10708357
#SPJ4
Juan has 3 blue markers and 4 red markers in his book bag. He randomly chooses 6 markers from the bag. Which event is certain
Answers
The event of Juan choosing at least one blue marker from the bag when randomly selecting 6 markers is certain.
In this scenario, Juan has a total of 7 markers in his bag, with 3 blue markers and 4 red markers. When he randomly chooses 6 markers from the bag, it is certain that he will select at least one blue marker. This is because there are more blue markers (3) than the number of markers he is selecting (6).
To understand why this event is certain, consider the worst-case scenario where Juan selects all 4 red markers first. Even in this case, there will still be 2 markers left in the bag, both of which are blue. Therefore, Juan is guaranteed to choose at least one blue marker when selecting 6 markers from the bag.
Since there are more blue markers available than the number of markers Juan is choosing, it is certain that he will select at least one blue marker. This makes the event of choosing at least one blue marker from the bag when randomly selecting 6 markers a certain event.
Learn more about certain event here:
https://brainly.com/question/32025802
#SPJ11
Two congruent ellipses are perpendicular to each other. Squares fill the gaps between the two ellipses as shown. Show that the side of the square equals half the minor axis of the ellipse.
Answers
The side of the square equals half the minor axis of the ellipse.
To show that the side of the square is half the minor axis of the ellipse, we must prove that the angles of the ellipses and the squares are congruent. To do this, we must first draw in the diagonals of the square, which will form two additional isosceles triangles.
Since the ellipses are perpendicular, the angles of the ellipses and the squares will be the same. Since the angles of the isosceles triangles are equal, the side of the square must be equal to half of the minor axis of the ellipse. Therefore, the side of the square is equal to half of the minor axis of the ellipse.
For more questions like Minor axis click the link below:
https://brainly.com/question/29054958
#SPJ4
How to express each of the following pairs of
simultaneous inequalities in the form
a * x * b where a and b are numbers and #
may be < or <,
(a) x > 3, 2x - 3 < 15
(b) 25 > 1 - 6x, 1 > 3x + 7
(c) 2x - 7<3< 27 + 4x
(d) 3x + 8 <0 < 21 + 4x
(e) 5x - 36 < -1 < 2x – 1
Answers
Answer:
a) 3<x<8
b) -4<x<-2
c) -6<x<5
d) -21/4 < x-8/3
e) 0<x<7
Step-by-step explanation:
Given the following inequalities
a) x > 3, 2x - 3 < 15
Solve 2x - 3 < 15
2x < 15+3
2x<18
x<18/2
x<8
Combine x>3 and x<8
If x>3, then 3<x
On combining, we have:
3<x<8
b) For the inequalities 25 > 1 - 6x, 1 > 3x + 7
25 > 1 - 6x
25-1>-6x
24>-6x
Divide through by -6:
24/-6 > -6x/-6
-4 <x
For the inequality 1 > 3x + 7
1-7>3x
-6>3x
-6/3 > 3x/3
-2 > x
x < -2
Combining both results i.e -4 <x and x < -2, we will have:
-4<x<-2
c) For the inequalities 2x - 7<3< 27 + 4x
On splitting:
2x - 7<3 and 3< 27 + 4x
2x < 3+7
2x<10
x<5
Also for 3< 27 + 4x
3-27<4x
-24<4x
-24/4 < 4x/4
-6<x
Combining both solutions i.e x<5 and -6<x will give;
-6<x<5
d) For the inequalities 3x + 8 <0 < 21 + 4x
3x + 8 <0
3x < -8
x < -8/3
Also for 0 < 21 + 4x
0-21<4x
-21<4x
-21/4 < 4x/4
-21/4 < x
Combining -21/4 < x and x < -8/3 will give;
-21/4 < x-8/3
e) For the inequalities 5x - 36 < -1 < 2x – 1
Split:
5x - 36 < -1
5x < -1+36
5x<35
5x/5 < 35/5
x < 7
For the expression -1 < 2x – 1
-1+1 < 2x
0 < 2x
0<x
Combining both inequalities 0<x and x < 7 will give:
0<x<7
∫(0 to [infinity]) x/(1+x2)2 dx is?
A. 1/2
B. 1
C. π/2
D. divergent
Answers
The value of the integral is 1/2. Your answer is: A. 1/2
How to find a definite integral using substitution and determining its value?the integral ∫(0 to ∞) x/(1+x²)² dx. Let's evaluate the integral and see which option fits:
The integral in question is:
∫(0 to ∞) x/(1+x²)² dx
To solve this integral, we can use the substitution method:
Let u = 1 + x². Then, du = 2x dx.
Now, we change the limits of integration:
When x = 0, u = 1 + 0² = 1.
When x -> ∞, u -> ∞.
Now, we substitute x and dx in the integral and update the limits:
∫(1 to ∞) (1/2) du/u²
This is an improper integral, so we have to take the limit as b -> ∞:
lim(b -> ∞) ∫(1 to b) (1/2) du/u²
Now, we integrate with respect to u:
lim(b -> ∞) [-1/2 * 1/u] evaluated from 1 to b
Now, evaluate the limit:
lim(b -> ∞) [-1/2 * (1/b - 1)]
As b -> ∞, 1/b -> 0:
-1/2 * (-1) = 1/2
So, the value of the integral is 1/2. Your answer is:
A. 1/2
Learn more about definite integral.
brainly.com/question/29685762
#SPJ11
Mae Ling earns a weekly salary of $365 plus a 5.0% commission on sales at a gift shop. How much she make in a workweek if she sold $4,800 worth of merchandise?
Answers
The amount that she make in a workweek if she sold $4,800 worth of merchandise will be $605.
How to calculate the value?A percentage is a value or ratio that may be stated as a fraction of 100. If we need to calculate a percentage of a number, we should divide it's entirety and then multiply it by 100.
Here, Mae Ling earns a weekly salary of $365 plus a 5.0% commission on sales at a gift shop.
The amount that she make in a workweek if she sold $4,800 worth of merchandise will be:
= $365 + (5% × $4800)
= $605
The amount is $605.
Learn more about percentages on:
brainly.com/question/24877689
#SPJ1
Consider the following vector field.
F(x, y, z) =
9ex sin(y), 2ey sin(z), 8ez
sin(x)
(a)
Find the curl of the vector field.
curl(F) =
(b)
Find the divergence of the vector field.
div(F) =
Answers
The curl of the vector field
curl(F) = -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
The divergence of the vector field
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
To find the curl of the vector field F(x, y, z) = 9ex sin(y), 2ey sin(z), 8ez sin(x), we need to compute the determinant of the curl matrix.
(a) Curl of F:
The curl of a vector field F = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k is given by the following formula:
curl(F) = (∂R/∂y - ∂Q/∂z)i + (∂P/∂z - ∂R/∂x)j + (∂Q/∂x - ∂P/∂y)k
In this case, we have:
P(x, y, z) = 9ex sin(y)
Q(x, y, z) = 2ey sin(z)
R(x, y, z) = 8ez sin(x)
Taking the partial derivatives, we get:
∂P/∂y = 9ex cos(y)
∂Q/∂z = 2ey cos(z)
∂R/∂x = 8ez cos(x)
∂R/∂y = 0 (no y-dependence in R)
∂Q/∂x = 0 (no x-dependence in Q)
∂P/∂z = 0 (no z-dependence in P)
Substituting these values into the curl formula, we have:
curl(F) = (0 - 2ey cos(z))i + (8ez cos(x) - 0)j + (0 - 9ex cos(y))k
= -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
Therefore, the curl of the vector field F is given by:
curl(F) = -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
(b) Divergence of F:
The divergence of a vector field F = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k is given by the following formula:
div(F) = ∂P/∂x + ∂Q/∂y + ∂R/∂z
In this case, we have:
∂P/∂x = 9e^x sin(y)
∂Q/∂y = 2e^y sin(z)
∂R/∂z = 8e^z
Substituting these values into the divergence formula, we have:
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
Therefore, the divergence of the vector field F is given by:
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
Learn more about divergence of the vector this link:
https://brainly.com/question/30907324
#SPJ11
Mrs. Yakubov needs to distribute 4 colored pencils and 3 glue sticks to the 6 tables in her classroom. Which expression represents the number of materials being distributed this situation? *
Answers
Answer:
The expression that represents the number of materials being distributed this situation is;
\(6(4+3)\)Explanation:
Let P and G represent the number of coloured pencils and glue sticks to be distributed;
\(P+G\)For 6 tables we have;
\(6(P+G)\)Given;
\(\begin{gathered} P=4 \\ G=3 \end{gathered}\)So, we have;
\(6(4+3)\)The expression that represents the number of materials being distributed this situation is;
\(6(4+3)\)let f ( x ) = ∫ x 2 0 ( sin t ) d t . at how many points in the closed interval [ 0 , √ π ] does the instantaneous rate of change of f equal the average rate of change of f on that interval
Answers
The instantaneous rate of change of f equals the average rate of change of f at 2 points in the closed interval [0, √π]: x = 0.673 and x = 1.325.
How did we get the values?To find the points in the closed interval where the instantaneous rate of change of f equals the average rate of change of f, we need to set up the equation for the derivative of f and the formula for the average rate of change of f on the interval.
First, we can evaluate the integral to get:
f(x) = ∫x^2 0 (sin t) dt = 1 - cos x^2
Next, we can find the derivative of f:
f'(x) = sin x^2 * 2x
To find the average rate of change of f on the interval [0, √π], we can use the formula:
Average rate of change of f = [f(√π) - f(0)] / (√π - 0)
= [1 - cos π] / √π
= 2 / √π
Now, we can set up the equation:
f'(x) = 2 / √π
sin x^2 * 2x = 2 / √π
sin x^2 = 1 / (√π x)
We can solve for x numerically using a graphing calculator or computer software. The solutions are approximately x = 0.673 and x = 1.325. Since these solutions are within the interval [0, √π], they are valid solutions.
Therefore, the instantaneous rate of change of f equals the average rate of change of f at 2 points in the closed interval [0, √π]: x = 0.673 and x = 1.325.
learn more about instantaneous rate of change: https://brainly.com/question/28684440
#SPJ1
An ice cream stand sells three different flavors of ice cream: vanilla, chocolate, and strawberry. Each gallon of vanilla costs $6.00 to purchase, each gallon of chocolate costs $6.50 to purchase, and each gallon of strawberry costs $7.00 to purchase. On average, the stand has 8 gallons of vanilla, 6 gallons of chocolate, and 4 gallons of strawberry in inventory and 1.5 days-of-supply. Each gallon of ice cream serves 16 customers, on average. How many customers does the ice cream stand expect to serve each day?
Answers
The ice cream stand expects to serve 288 customers each day.
To calculate the expected number of customers the ice cream stand expects to serve each day, we need to multiply the gallons of each flavor by the number of customers served per gallon and then sum up the results.
Let's denote:
V = Gallons of vanilla = 8
C = Gallons of chocolate = 6
S = Gallons of strawberry = 4
D = Days-of-supply = 1.5
Serving per gallon = 16
The number of customers served each day can be calculated as follows:
Total customers = (V * Serving per gallon) + (C * Serving per gallon) + (S * Serving per gallon)
Total customers = (8 * 16) + (6 * 16) + (4 * 16)
Total customers = 128 + 96 + 64
Total customers = 288
To determine the number of customers served each day, we need to multiply the gallons of each flavor by the number of customers served per gallon and sum up the results. In this case, the stand has 8 gallons of vanilla, 6 gallons of chocolate, and 4 gallons of strawberry. Given that each gallon serves an average of 16 customers, we can calculate the number of customers served for each flavor by multiplying the gallons by the serving per gallon. Finally, by summing up the customers served for each flavor, we obtain the total number of customers served per day, which in this case is 288.
Learn more about customers here:-
https://brainly.com/question/29255658
#SPJ11
ABCD is a parallelogram.
Answers
Answer:
It is
Step-by-step explanation:
If the ratio of lengths between two similar solid is 5 to 8, what is the ratio of their volumes?
Answers
The ratio of the volumes as per the given length ratio is equal to 125:512.
The ratio of the volumes of two similar solids is equal to the cube of the ratio of their corresponding lengths.
Let's denote the ratio of lengths between the two similar solids as a:b.
Here, a:b = 5:8.
The ratio of their volumes (V₁ : V₂) is given by,
V₁ : V₂= (a³) : (b³)
Substituting the given values, we get:
V₁ : V₂
= (5³) : (8³)
= 125 : 512
Therefore, the ratio of their volumes is 125:512.
Learn more about volume here
brainly.com/question/10109192
#SPJ4
00 Q) Determine whether {(und)"} 3" Converges or diverges no
Answers
We can say that {(und)"} 3" diverges because it is a geometric sequence with a common ratio of 3, which is greater than 1.
To determine whether the sequence {(und)"} 3" converges or diverges, we need to look at the behavior of the terms as n gets larger.
We can start by writing out the first few terms of the sequence:
{(und)"} 3" = 3, 9, 27, 81, ...
We can see that each term is simply the previous term multiplied by 3. This means that the sequence is a geometric sequence with a common ratio of 3.
In general, a geometric sequence with a common ratio r will converge if |r| < 1 and diverge if |r| ≥ 1.
In the case of {(und)"} 3", the common ratio is 3, which is greater than 1. Therefore, the sequence diverges.
To summarize, we can say that {(und)"} 3" diverges because it is a geometric sequence with a common ratio of 3, which is greater than 1.
Learn more about diverges here:
https://brainly.com/question/30889536
#SPJ11
Solve m +1.4 = 0.6.
What does m equal?
Answers
Answer:
m=0.8
Step-by-step explanation:
Answer:
0.8
Step-by-step explanation:
1.4-0.6=m
NEED HELP ASAP ASAP!!!!!
