what is the length of BC, AC, ED, DK, &’ EK?
sorry there’s so many!! i tried putting it at 25 points!!!!! PLEASE PLEASE HELP ME THIS IS 4 A TEST

Answers
For the truth
am not sure
Answer:
BC = 12, AC = 12, ED = 8, DK = 14, EK = 12
Related Questions
A pet store increases the price of a bag of dog food by 5%
If the increase in price is $2.00, what is the new price for dog food?
Answers
Answer:
$42.00
Step-by-step explanation:
We can represent the given information as a ratio:
% of original price : price
5% : $2.00
Then, we can multiply both sides of this ratio by 20 (or 100% / 5%) to get 100% of the original price, which IS the original price.
5% : $2.00
↓ × 20 ↓ × 20
100% : $40.00
Now that we know the original price, we can add $2.00 to get the new price.
$40.00 + $2.00 = $42.00
12. The calculation of property tax is based on the
Answers
The tax revenue generated from property taxes is often used to fund expressions public services such as schools, parks, and infrastructure projects in the local community.
what is expression ?In mathematics, you can multiply, divide, add, or subtract. An expression is constructed as follows: Number, expression, and mathematical operator A mathematical expression is made up of numbers, variables, and functions (such as addition, subtraction, multiplication or division etc.) It is possible to contrast expressions and phrases. An expression or algebraic expression is any mathematical statement that has variables, integers, and an arithmetic operation between them. For example, the expression 4m + 5 has the terms 4m and 5, as well as the provided expression's variable m, all separated by the arithmetic sign +. The calculation of property tax is typically based on the assessed value of the property and the tax rate set by the local government. The assessed value is determined by a government-appointed assessor who evaluates the value of the property based on factors such as its location, size, age, and condition. The tax rate is then applied to the assessed value to determine the amount of tax owed by the property owner. The tax revenue generated from property taxes is often used to fund public services such as schools, parks, and infrastructure projects in the local community.
To know more about expressions visit :-
https://brainly.com/question/14083225
#SPJ1
A savings account increased by $75 is now more than $500. What is the least amount of money that was originally put in the savings account?
Answers
The least amount of money that was originally put in the savings account is $426.
What is the least amount of money?The amount of money in the savings account is a function of the money that was originally in the account and the amount by which the account was increased by.
The inequality that represents the total amount of money in the savings account is:
amount originally in the account + amount deposited > 500
x + $75 > $500
x > $500 - $75
x > $425
The least amount would be $426 because this is the smallest number that is greater than $425 that would make the total amount more than $500.
To check:
$75 + $426 = $501
To learn more about savings, please check: https://brainly.com/question/28727268
#SPJ1
Write in Slope Intercept Form :-)

Answers
y = -5x + 2
Explanation:

A. Use a triple integral to find the volume of the given solid. The tetrahedron enclosed by the coordinate planes and the plane8x + y + z = 2B. Find the volume of the smaller wedge cut from a sphere of radius 4 by two planes that intersect along a diameter at an angle of π/6.
Answers
The volume of the smaller wedge cut from a sphere of radius 4 by two planes that intersect along a diameter at an angle of π/6 is 1/6.
What is volume ?
Volume is a measurement of three-dimensional space that is occupied. It is frequently expressed quantitatively using SI-derived units, as well as several imperial or US-standard units. Volume and the notion of length are connected.
Consider that the tetrahedron is bounded by the coordinate planes and the plane 8 x+y+z=2
Evaluate the triple integral \(\iiint_E d V$.\)
The lower boundary of tetrahedron is the plane z=0 and the upper boundary of tetrahedron is the plane z=2-8 x-y.
And the projection is y=2-8 x.
The x-limits are obtained by taking y=0 and z=0 in 8 x+y+z=2.
\($$\begin{array}{r}8 x=2 \\x=\frac{2}{8} \\x=\frac{1}{4}\end{array}$$\)
Therefore, the region becomes \($R=\left\{(x, y, z) / 0 \leq x \leq \frac{1}{4}, 0 \leq y \leq 2-8 x, 0 \leq z \leq 2-8 x-y\right\}$\).
Therefore, the integral becomes
\($ \iiint_E d V=\int_0^{\frac{1}{4}} \int_0^{2-8 x} \int_0^{2-8 x-y} d z d y d x $\)
\($=\int_0^{\frac{1}{4}} \int_0^{2-8 x}[z]_0^{2-8 x-y} d y d x $\)
\($ =\int_0^{\frac{1}{4}} \int_0^{2-8 x}[2-8 x-y] d y d x $\)
\($ =\int_0^{\frac{1}{4}}\left[2 y-8 x y-\frac{y^2}{2}\right]_0^{2-8 x} d x . $\)
\($ =\int_0^{\frac{1}{4}}\left[2(2-8 x)-8 x(2-8 x)-\frac{(2-8 x)^2}{2}\right] d x $\)
\($ =\int_0^{\frac{1}{4}}\left[32 x^2-16 x+2\right] d x $\)
\($ =\left[32\left(\frac{x^3}{3}\right)-16\left(\frac{x^2}{2}\right)+2 x\right]_0 $\)
\($ =32\left(\frac{\left(\frac{1}{4}\right)^3}{3}\right)-16\left(\frac{\left(\frac{1}{4}\right)^2}{2}\right)+2\left(\frac{1}{4}\right)-0 $\)
\($ =\frac{1}{6} $\)
To learn more about Volume visit:https://brainly.com/question/13338592
#SPJ4
Right triangle with a hypotenuse of 159 ft and Angle A = 34 degree
Calculate the length of the sides they should be rounded to the nearest whole foot. The rounded for the legs (side) should be used to calculate the area of the triangle
Answers
the length of side a is 91 ft (rounded to the nearest whole foot) and the length of side b is 132 ft (rounded to the nearest whole foot). The area of the triangle is approximately 6007 sq ft.
Given: The hypotenuse of the right triangle,
c = 159 ft; angle A = 34°
We know that, in a right-angled triangle:
\($$\sin\theta=\frac{\text{opposite}}\)
\({\text{hypotenuse}}$$$$\cos\theta=\frac{\text{adjacent}}\)
\({\text{hypotenuse}}$$\)
We know the value of the hypotenuse and angle A. Using trigonometric ratios, we can find the length of sides in the right triangle.We will use the following formulas:
\($$\sin\theta=\frac{\text{opposite}}\)
\({\text{hypotenuse}}$$$$\cos\theta=\frac{\text{adjacent}}\)
\({\text{hypotenuse}}$$$$\tan\theta=\frac{\text{opposite}}\)
\({\text{adjacent}}$$\) Length of side a is:
\($$\begin{aligned} \sin A &=\frac{a}{c}\\ a &=c \sin A\\ &= 159\sin 34°\\ &= 91.4 \text{ ft} \end{aligned}$$Length of side b is:$$\begin{aligned} \cos A &=\frac{b}{c}\\ b &=c \cos A\\ &= 159\cos 34°\\ &= 131.5 \text{ ft} \end{aligned}$$\)
Now, we have the values of all sides of the right triangle. We can calculate the area of the triangle by using the formula for the area of a right triangle:
\($$\text{Area} = \frac{1}{2}ab$$\)
Putting the values of a and b:
\($$\begin{aligned} \text{Area} &=\frac{1}{2}ab\\ &=\frac{1}{2}(91.4)(131.5)\\ &= 6006.55 \approx 6007 \text{ sq ft}\end{aligned}$$\)
Therefore, the length of side a is 91 ft (rounded to the nearest whole foot) and the length of side b is 132 ft (rounded to the nearest whole foot). The area of the triangle is approximately 6007 sq ft.
For more question triangle
https://brainly.com/question/29135702
#SPJ8
7. At the Go Nutty Peanut Company, dry roasted, shelled peanuts are placed in jars by a machine. The
distribution of weights in the glass jars is approximately Normal, with a mean of 17 ounces and a standard
deviation of 0.68 ounces (3 points)
a. What is the probability of randomly selecting 50 jars and finding the average contents to weigh less
than 16.8 ounces?
Answers
The probability of selecting 50 jars is 0%
The z score determines by how many standard deviations the raw score is above or below the mean. It is given by:
\(z=\frac{x-\mu}{\sigma/\sqrt{n} } \\\\where \mu=mean,\sigma=standard\ deviation, x=raw\ score,n=sample\ size\\\\Given\ that\ \mu=17,\sigma=0.68,n=50,x=16.8\\\\z=\frac{16.8-17}{0.65/\sqrt{50} } =-5\)
The P(z < -5) = 0%
Therefore the probability of selecting 50 jars is 0%
Find out more at: https://brainly.com/question/15016913
The function f(1) = 60,000(2)
00(2) 410 gives the number
of bacteria in a population & minutes after an initial
observation. How much time, in minutes, does it
take for the number of bacteria in the population to
double?
Answers
It takes 10 minutes for the number of bacteria in the population to double.
To determine the time it takes for the number of bacteria in a population to double, we need to find the value of t when the function f(t) equals twice the initial number of bacteria.
The given function is f(t) = 60,000 * 2^(t/10).
To find the time it takes for the number of bacteria to double, we set f(t) equal to twice the initial number of bacteria, which is 2 * 60,000 = 120,000:
120,000 = 60,000 * 2^(t/10).
Next, we can simplify the equation by dividing both sides by 60,000:
2 = 2^(t/10).
Since both sides of the equation have the same base (2), we can equate the exponents:
t/10 = 1.
To solve for t, we multiply both sides by 10:
t = 10.
Therefore, it takes 10 minutes for the number of bacteria in the population to double.
This result is obtained by setting the growth rate of the bacteria population in the given function. The exponent t/10 determines the rate of growth, and when t is equal to 10, the exponent becomes 1, resulting in a doubling of the initial number of bacteria.
For more scuh questions on population visit:
https://brainly.com/question/31243583
#SPJ8
Abby can buy an 8-pound bag of dog food for $7.40 or a 4-pound bag of the same dog food for $5.38. Which of the bags would be the best deal?
Answers
Given, Abby can buy an 8-pound bag of dog food for $7.40.
The cost of one pound bag when 8-pound bag of dog food for $7.40 is,
\(\begin{gathered} C=\frac{7.40}{8} \\ =0.925 \end{gathered}\)Given, 4-pound bag of the same dog food costs $5.38.
Therefore, the cost of one pound bag when 4-pound bag of dog food costs $5.38 is,
\(\begin{gathered} C=\frac{5.38}{4} \\ =1.345 \end{gathered}\)Since the cost of one pound bag has a smaller value(=0.925) when an 8-pound bag of dog food is bought, buying an 8-pound bag of dog food for $7.40 would be the best deal.
Find the distance between the points (-6, - 4) and (5, -4).
Answers
Answer:
\(d=11\)
Step-by-step explanation:
Distance Formula: \(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Simply plug in your 2 coordinates into the distance formula to find distance d:
\(d=\sqrt{(5-(-6))^2+(-4-(-4))^2}\)
\(d=\sqrt{(5+6)^2+(-4+4)^2}\)
\(d=\sqrt{(11)^2+(0)^2}\)
\(d=\sqrt{121+0}\)
\(d=\sqrt{121}\)
\(d=11\)
find the slope of the line that passes through the points (20,8) and (9,16)
Answers
Answer:
slope: \(-\frac{8}{11}\)
slope-intercept form: y= \(-\frac{8}{11}\)x+\(\frac{248}{11}\)
Step-by-step explanation:
Hope this helps!
how to graph the line Y= (1/4)x - 3
Answers
Solution:
Given:
\(y=\frac{1}{4}x-3\)To graph the line, at least the coordinates of two points are needed.
Using the x and y-intercepts;
\(\begin{gathered} x-intercept: \\ when\text{ y = 0} \\ 0=\frac{x}{4}-3 \\ 0+3=\frac{x}{4} \\ 3=\frac{x}{4} \\ x=3\times4 \\ x=12 \\ x-intercept=(12,0) \end{gathered}\)\(\begin{gathered} y-intercept: \\ when\text{ x = 0} \\ y=\frac{1}{4}(0)-3 \\ y=0-3 \\ y=-3 \\ y-intercept=(0,-3) \end{gathered}\)Using the two points, the graph of the line is shown;

What is the distance between the points (6,2) and (1,-5)
PLEASE ANSWER QUICK
Answers
Answer:
\(\displaystyle d = \sqrt{74}\)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Coordinates (x, y)Algebra II
Distance Formula: \(\displaystyle d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)Step-by-step explanation:
Step 1: Define
Point (6, 2) → x₁ = 6, y₁ = 2
Point (1, -5) → x₂ = 1, y₂ = -5
Step 2: Find distance d
Simply plug in the 2 coordinates into the distance formula to find distance d
Substitute in points [Distance Formula]: \(\displaystyle d = \sqrt{(1-6)^2+(-5-2)^2}\)[Distance] [√Radical] (Parenthesis) Subtract: \(\displaystyle d = \sqrt{(-5)^2+(-7)^2}\)[Distance] [√Radical] Evaluate exponents: \(\displaystyle d = \sqrt{25+49}\)[Distance] [√Radical] Add: \(\displaystyle d = \sqrt{74}\)Henry wants to create a vegetable garden in his backyard against the back wall of his
house. He has 60 feet fence to protect the garden from the deer. What is the maximum
area of the garden he can create (in square feet)?
Answers
Which ordered pair represents 3 points to the left and 2 points above T
Answers
Answer:
Answer:
(0, 6)
Step-by-step explanation:
Point T has a coordinate pair of (3, 4). That is, at point T, x = 3, while y = 4.
3 points to the left of T would be a movement on the x-axis. This movement is a run across the x-axis. At T, x = 3. Therefore, 3 points to the left would be a decrease by 3 = 3 - 3 = 0.
3 points to the left of T would leave us with an x coordinate of 0.
2 points above T suggest a rise, which is on the y-axis.
Therefore, at T, y = 4. 2 points above 4 = 4 + 2 = 6. y coordinate would now be 6.
In conclusion, the ordered pair representing 3 points to the left, and 2 points above point T is (0, 6).
Answer:
(0, 6)
Step-by-step explanation:
Need help asap please!

Answers
Answer:
The distance of two complex numbers
\(z_{1} z_{2} = \sqrt{82}\) = 9.055
Step-by-step explanation:
Step(i):-
Given that z₁ = 6-3i and z₂ = -3-4i
We know that 'z' represents a point on the argand plane with absicca 'x' and ordinate 'y'
Now given points are ( x₁ , y₁) = (6 ,-3) and (x₂, y₂) = (-3 , -4)
Step(ii):-
The distance of two points
\(\sqrt{(x_{2} -x_{1} )^{2} +(y_{2} - y_{1} )^{2} }\)
z₁ z₂ \(= \sqrt{(-3-6)^{2} +(-4-(-3)^{2} }\)
\(z_{1} z_{2} = \sqrt{81+1}\)
\(z_{1} z_{2} = \sqrt{82}\) =9.055
Two siblings, sibling A and sibling B, are saving money for their summer vacation. The amount of money that sibling A has in their savings account, y, can be represented by the equation y = 10x + 25, where x represents the number of weeks. Sibling B's savings can be represented by the equation y = 5x + 50. Based on the graph of this system of linear equations, after how many weeks will their savings accounts have the same amount of money? 2.5 weeks 5 weeks 15 weeks 75 weeks
Answers
Answer: 5 weeks
Explanation:
To find out when both siblings will have the same amount of money in their savings accounts, we need to solve the system of equations:
y = 10x + 25
y = 5x + 50
We can set the two equations equal to each other and solve for x:
10x + 25 = 5x + 50
5x = 25
x = 5
Therefore, after 5 weeks, both siblings will have the same amount of money in their savings accounts. So the answer is 5 weeks.
no spam
The linear function f(x) = 0.5x + 80 represents the average test score in your math class, where x is the number of the test taken. The linear function g(x) represents the average test score in your science class, where x is the number of the test taken.
x g(x)
1 81
2 83
3 85
Part A: Determine the test average for your math class after completing test 2. (2 points)
Part B: Determine the test average for your science class after the completing test 2. (2 points)
Part C: Which class had a higher average after completing test 4? Show work to support your answer. (6 points)
Answers
Table
\(\boxed{\begin{array}{c|c}\boxed{\bf x} &\boxed{\bf g(x)} \\ \sf 1&\sf 81 \\ \sf 2&\sf 83 \\ \sf 3&\sf 85\\ \sf 4 &\sf 87(Expected)\end{array}}\)
\(\boxed{\begin{array}{c|c}\boxed{\bf x} &\boxed{\bf f(x)} \\ \sf 1&\sf 80.5 \\ \sf 2&\sf 81 \\ \sf 3&\sf 81.5 \\ \sf 4&\sf 82\end{array}}\)
Now
#Part A:-
Test average for completing test 2 in maths=81
#Part-B
Test average for completing test 2in science=83
#Part C.
CLASS B HAS HIGHER AVERAGEA mail-order computer business has six telephone lines. Let X denote the number of lines in use at a specified time. Suppose the pmf of X is as given in the accompanying table.
x 0 1 2 3 4 5 6
p(x) 0.12 0.18 0.20 0.20 0.20 0.07 0.03
Calculate the cdf F(x).
x 0 1 2 3 4 5 6
f(x)
Use the graph to calculate the probabilities of the events given below.
(a) {at most three lines are in use}
(b) {fewer than three lines are in use}
(c) {at least three lines are in use}
(d) {between two and five lines, inclusive, are in use}
Answers
The probability of the event between two and five lines, inclusive, are in use is 0.85.
What is the probability?Probability can be defined as the ratio of the number of favourable outcomes to the total number of outcomes of an event.
Given that,
x 0 1 2 3 4 5 6
p(x) 0.12 0.18 0.20 0.20 0.20 0.07 0.03
a) At most three lines are in use
Here we need to find the probability for x≤3.
P(x≤3)=P(x=0)+P(x=1)+P(x=2)+P(x=3)
= 0.12+0.18+0.20+0.20
= 0.70
b) Fewer than three lines are in use
Here we need to find the probability for x<3.
P(x<3)=P(x=0)+P(x=1)+P(x=2)
= 0.12+0.18+0.20
= 0.50
c) At least three lines are in use
Here we need to find the probability for x≥3.
P(x≥3)=P(x=3)+P(x=4)+P(x=5)+P(x=6)
= 0.20+0.20+0.07+0.03
= 0.50
d) Between two and five lines, inclusive, are in use
Here we need to find the probability for 2≤x≤5.
P(2≤x≤5)= P(x=2)+P(x=3)+P(x=4)+P(x=5)
= 0.18+0.20+0.20+0.20+0.07
= 0.85
Therefore, the probability of the event between two and five lines, inclusive, are in use is 0.85.
To learn more about the probability visit:
https://brainly.com/question/11234923.
#SPJ1
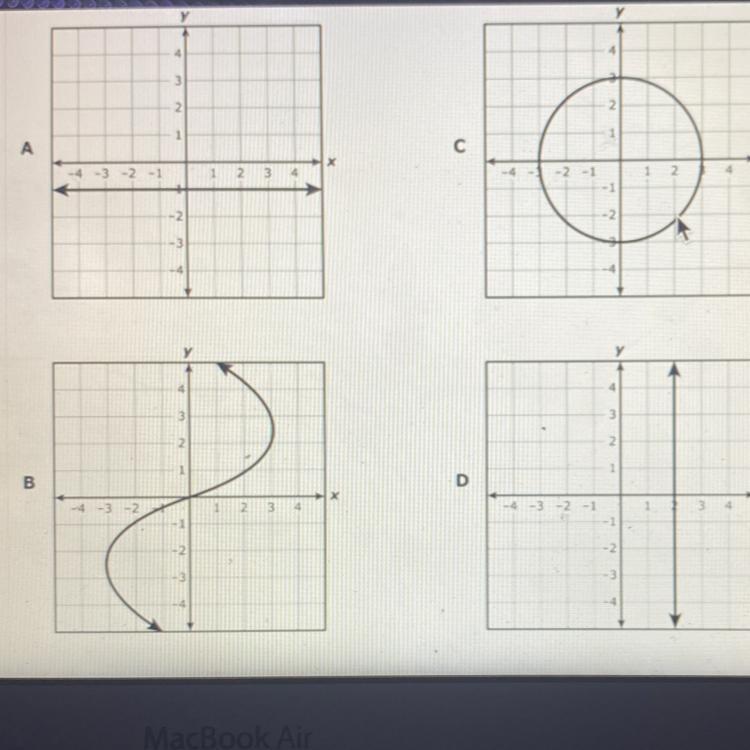
Which graph represents y as a function of x?
Answers
Answer:
D
Step-by-step explanation:
Has only one point on the x- axis.
Please help for a grade

Answers
The situation that cannot be modeled by using an exponential function is A. Jim buys a golf membership for $ 150 and it costs him $ 11 each time he plays a round of golf.
What can are exponential functions ?Exponential functions are mathematical functions in which the variable (usually denoted by "x") is in the exponent, rather than the base. They take the form of f(x) = a^x, where a is a constant known as the base of the function, and x is the input variable. These functions are characterized by rapid growth or decay as x increases or decreases.
The situation where Jim buys a golf membership cannot be modelled this way as it is a linear function because there is a given rate of increase that is not exponential.
Find out more on exponential functions at https://brainly.com/question/2456547
#SPJ1
checK if x=2 is a solution of a) 7x+5=21 b 2*-2=2
Answers
Answer:
First, substitute x for 2 in 7x+5=21.
7 * 2 = 14 + 5 = 19
x = 2 is not a solution of 7x+5=21.
Consider a sample with data values of 26, 27, 20, 15, 30, 34, 28, and 20. Compute the range, interquartile range, variance, and standard deviation (to a maximum of 2 decimals, if decimals are necessary).
Answers
Answer:
\(r=19\)
\(IQR=9\)
\(SD=5.81\)
Step-by-step explanation:
Given the following data set:
\(26, 27, 20, 15, 30, 34, 28,20\)
To find the range of a data set we have to find the largest and the smallest number of the set and then subtract them.
\(26, 27, 20, 15, 30, 34, 28,20\)
\(34-15=19\)
\(r=19\)
To find the interquartile range we have to subtract the third quartile by the first quartile.
\(26, 27, 20, 15, 30, 34, 28,20\)
\(IQR=Q3-Q1\)
\(Q1=20\)
\(Q3=29\)
\(IQR=29-20=9\)
\(IQR=9\)
To find the standard deviation of a data set we have to use the formula to calculate standard deviation with the given values.
\(SD=\frac{(26-25)^2+...+(20-25)^2}{8}\)
\(SD=\frac{270}{8} =\sqrt{33.75} =5.8094750193111\)
\(5.8094750193111\)
\(9>5\)
\(SD=5.81\)
Hope this helps.
PLEASE HELP!!!!! (31 POINTS!) Fill in the arithmetic table

Answers
The table for this arithmetic sequence should be completed as follows:
Position 1 6 8 11 19 25
Term 0 -10 -14 -20 -36 -48
How to calculate an arithmetic sequence?Mathematically, the nth term of an arithmetic sequence can be calculated by using this expression:
aₙ = a₁ + (n - 1)d
Where:
d represents the common difference.a₁ represents the first term of an arithmetic sequence.n represents the total number of terms.Next, we would determine the common difference by using the 25th term of this arithmetic sequence:
-48 = 0 + (25 - 1)d
-48 = 24d
d = -48/2
d = -2.
For the nth term of this arithmetic sequence with -10, we have:
aₙ = a₁ + (n - 1)d
-10 = 0 + (n - 1)-2
-10 = -2n + 2
2n = 12
n = 6.
For the 8th term of this arithmetic sequence, we have:
a₈ = a₁ + (n - 1)d
a₈ = 0 + (8 - 1)-2
a₈ = -14.
For the nth term of this arithmetic sequence with -20, we have:
aₙ = a₁ + (n - 1)d
-20 = 0 + (n - 1)-2
-20 = -2n + 2
2n = 22
n = 11.
For the 19th term of this arithmetic sequence, we have:
a₁₉ = a₁ + (n - 1)d
a₁₉ = 0 + (19 - 1)-2
a₁₉ = -36.
Read more on arithmetic sequence here: brainly.com/question/24989563
#SPJ1
If a 4 digit number 4ab5 is divisible by 55 then determine the value of b-a
Answers
Answer:
Step-by-step explanation:
Solution:
A four-digit number 4ab5 is divisible by 55. Then the value of b - a is 1.
Falling objects can be modeled with quadratic functions. One student was thinking about this
and wondered what might happen in a few different situations.
They wondered if they could get on top of a 126 foot tall building and throw a tennis ball
straight up in the air as hard as they could, how long would it take for the ball to hit the ground.
Based on their knowledge of gravity and how fast they can throw a ball, they created the
following equation, which relates time, t, in seconds to height, h(t), in feet.
h(t) = -14t² + 56t+126
a. Find the vertex of the equation and explain what it means in this context.
b. Find the x-intercepts and y-intercept and explain what they mean in this context.
This student also wonders how long it will take the ball to reach the 6th floor, which
they measured to be 72 feet from the ground. Find the time it will take for the ball to reach 72 feet.
Answers
a. The x-coordinate of the vertex (2) represents the time it takes for the ball to reach its maximum height, and the y-coordinate (182) represents the maximum height itself.
b. The tennis ball is initially at a height of 126 feet above the ground.
How to calculate the valuea. The x-coordinate of the vertex is 2. To find the y-coordinate, we substitute this value back into the equation:
h(2) = -14(2)² + 56(2) + 126
h(2) = -14(4) + 112 + 126
h(2) = -56 + 112 + 126
h(2) = 182
Therefore, the vertex of the equation is (2, 182). In this context, the vertex represents the highest point reached by the tennis ball during its trajectory. The x-coordinate of the vertex (2) represents the time it takes for the ball to reach its maximum height, and the y-coordinate (182) represents the maximum height itself.
b. In order to find the y-intercept, we set t equal to zero and evaluate h(t):
h(0) = -14(0)² + 56(0) + 126
h(0) = 126
The y-intercept is 126. In this context, the y-intercept represents the initial height of the ball when it is thrown. Therefore, the tennis ball is initially at a height of 126 feet above the ground.
Learn more about equations
https://brainly.com/question/2972832
#SPJ1
$2.95+$3.09+$5.85+$4.10
Answers
Step-by-step explanation:
the value of P(B|A)P(B∣A), rounding to the nearest thousandth
$15.99
Explanation:
All you have to do is add them together
the daily totals of enrollments at sunny side daycare last monday through saturday were 17, 19, 23, 14, 25, and 28
Answers
The average number of enrollments per day at the Sunnyside Daycare is 21.
What is an average?An average is a result obtained by summing some numerical values and then dividing the total by the number of values or variables.
An average is the mean, which is one of the central tendency values.
Data and Calculations:Day Number of Enrollments
Monday 17
Tuesday 19
Wednesday 23
Thursday 14
Friday 25
Saturday 28
Total = 126
Average enrollments = 21 (126/6)
Thus, the average number of enrollments per day at the Sunnyside Daycare is 21.
Learn more about finding average values at https://brainly.com/question/11874959
#SPJ1
Question Completion:What was the average number of enrollments per day?
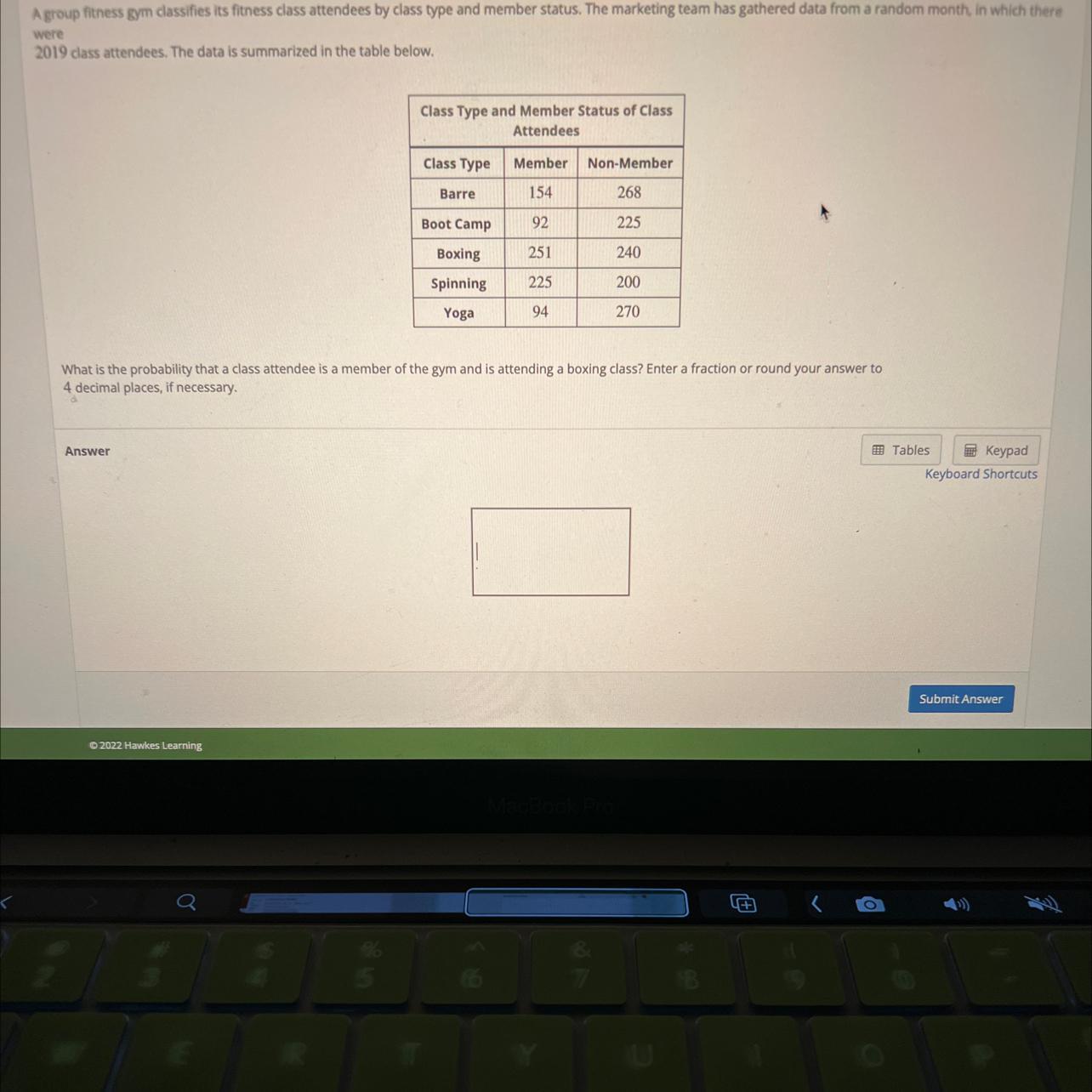
A group fitness gym classifies its fitness class attendees by class type and member status. The marketing team has gathered data from a random month, in which thereWere2019 class attendees. The data is summarized in the table below.What is the probability that a class attendee is a member of the gym and is attending a boxing class? Enter a fraction or round your answer to4 decimal places, if necessary.
Answers
Member of the gym: (154 + 92 + 251 + 225 + 94 ) = 816
Boxing class = 251 (member)
Boxing/ total members = 251 / 816 = 0.3076
TARGET SELLS 24 BOTTELS OF WATER FOR 3 DOLARS AND 36 DOLARS WHICH IS THE BETTER BUY AND BY HOW MUCH
Answers
Answer:
The 36-pack is a better buy by $0.50 per 36 bottles.
Step-by-step explanation:
24 bottles for $3 compared to 36 bottles for $4
Unit rates:
$3/24 = $0.125/bottle
$4/36 = $0.111/bottle
The 36-pack is a better buy since the unit price is lower.
$0.125 - $0.111 = $0.013888...
$0.01388888... * 36 = $0.50
Answer: The 36-pack is a better buy by $0.50 per 36 bottles.