Write each function in factored form. Check by multiplication. y=-2x³-2x²+40 x .
Answers
The multiplication confirms that the factored form -2x(x + 5)(x - 4) is equivalent to the original function -2x³ - 2x² + 40x.
To write the function y = -2x³ - 2x² + 40x in factored form, we can factor out the greatest common factor (-2x) from each term:
y = -2x(x² + x - 20)
Now, let's factor the quadratic expression (x² + x - 20) further:
y = -2x(x + 5)(x - 4)
To check this factored form, we can multiply the factors together:
-2x(x + 5)(x - 4) = -2x(x² - 4x + 5x - 20)
= -2x(x² + x - 20)
= -2x³ - 2x² + 40x
The multiplication confirms that the factored form -2x(x + 5)(x - 4) is equivalent to the original function -2x³ - 2x² + 40x.
Learn more about function here:
https://brainly.com/question/31062578
#SPJ11
Related Questions
Solve for x: 6x + 3 = 5x − 8 −11 11 −5 5
Answers
Step-by-step explanation:
6x + 3 = 5x - 8
x = -11
Bring x terms to LHS and constant terms to RHS
Topic: Algebraic equations
If you like to venture further, feel free to check out my insta (learntionary). It would be best if you could give it a follow. I'll be constantly posting math tips and notes! Thanks!
Answer:
-11
Step-by-step explanation:
What is an expression that is equivalent to 6x2 −19x−7?
Select options from the drop-down menus to correctly complete the equivalent expression.
Answers
Answer:
12+133
Step-by-step explanation:
Separate this expression into two parts, (6x2) + (-19x-7)
Solve what is in the parenthesis (12) + (133)= 12+133
The simplified expression would also be 145
The expression that is equivalent to 6x² −19x−7 would be (2 x - 7 ) ( 3x - 1)
What are equivalent expressions?Those expressions that might look different but their simplified forms are the same expressions are called equivalent expressions.
To derive equivalent expressions of some expressions, we can either make it look more complex or simple. Usually, we simplify it.
We need to find the expression into an equivalent form 6x² −19x−7
This expression could also be given by;
6x² −19x−7
Separate this expression into two parts;
(6x²) + (-19x-7)
Solve the parenthesis ;
3x (2 x - 7 ) -1 (2 x - 7 ) = 0
(2 x - 7 ) ( 3x - 1) = 0
The expression that is equivalent to 6x² −19x−7 would be (2 x - 7 ) ( 3x - 1)
Learn more about expression here;
brainly.com/question/14083225
#SPJ2
will someone plz help
by the way funny photo


Answers
110.859
Hi its me again
Answer:
1026
Step-by-step explanation:
as everyone knows that up to 4 the number increases so here it is 4 so it decreases we can't increase it .
hope it helps.
Weighted average cost flow method under perpetual inventory system the following units of a particular item were available for sale during the calendar year: jan. 1 inventory 10,000 units at $75.00 mar. 18 sale 8,000 units may 2 purchase 18,000 units at $77.50 aug. 9 sale 15,000 units oct. 20 purchase 7,000 units at $80.25
Answers
The weighted average cost per unit under the perpetual inventory system is $55.76.
To calculate the weighted average cost flow method under the perpetual inventory system, follow these steps:
1. Calculate the total cost of inventory on hand at the beginning of the year: 10,000 units * $75.00 = $750,000.
2. Calculate the cost of goods sold for each sale:
- For the first sale on March 18, the cost of goods sold is 8,000 units * $75.00 = $600,000.
- For the second sale on August 9, the cost of goods sold is 15,000 units * $77.50 = $1,162,500.
3. Calculate the total cost of purchases during the year:
- The purchase on May 2 is 18,000 units * $77.50 = $1,395,000.
- The purchase on October 20 is 7,000 units * $80.25 = $561,750.
- The total cost of purchases is $1,395,000 + $561,750 = $1,956,750.
4. Calculate the total number of units available for sale during the year: 10,000 units + 18,000 units + 7,000 units = 35,000 units.
5. Calculate the weighted average cost per unit: $1,956,750 ÷ 35,000 units = $55.76 per unit.
Learn more about cost of goods sold from the given link:
https://brainly.com/question/33405095
#SPJ11
Find the total balance of each investment account earning simple annual interest.
A: $624 at 5% for 3 years
B: $4,120 at 7% for 18 months
C: $900 at 3.1% for 6 months
D: $275 at 4.8% for 8 years
Answers
You should remember the formula: Interest = P * R * T /100
Apply it in every part.
A) I = 624 * 5 * 3 / 100
I = 9360/100
I = 93.60
So, Total amount = 93.60 + 624 = $717.60
B) I = 4120 * 7 * 3 / 2*100
I = 86520 / 200
I = 432.60
So, Total amount = 432.60 + 4120 = $4552.60
C) I = 900 * 3.1 * 1 / 2 * 100
I = 2790 / 200
I = 13.95
So, Total Amount = 13.95 + 900 = $913.95
D) I = 275 * 4.8 * 8 /100
I = 10560 / 100
I = 105.60
So, Total amount = 105.60 + 275 = $380.60
Hope this helps
What is the relation between area height and volume?
Answers
The relation between area, height and volume is: volume = area * height
In this question we need to find the relation between area height and volume.
the formula for area and volume are based on height:
volume = base area * height
Let v represents the volume, A represents area and h represents the height.
V = A * h
As we know the volume of rectangular prism is:
volume = length * width * height
i.e., V = l * w * h
and the base area is:
area = length * width
i.e., A = l * w
Substitute A = l * w in V = l * w * h
Then we get, V = A * h
Therefore, the relation between area, height and volume is: V = A * h i.e., volume = area * height
Learn more about the area, height and volume here:
https://brainly.com/question/19217739
#SPJ4
Suppose a continuous random variable X is uniformly distributed on the interval [4,9]. able Y distributed? That is, determine the probability density function fy(y) 1. None of these. 2. for 4-y-9 = 10, 0 otherwise
Answers
For a continuous random variable X, which is uniformly distributed on an interval [4,9], the probability density function of \(f_Y( y)\) is equals to
\(f_Y( y) =\begin{cases} \frac{2y}{5},\quad 2≤ x ≤ 3 \\ 0, \quad \: otherwise\ \ \end{cases}\). So, option(5) is correct.
We have a continuous random variable X is uniformly distributed on the interval [4,9]. The PDF is a probability that a random variable acquire a value exactly same or equal to the random variable but in case of CDF, this probability values is less than or equal to the random variable. The probability density function for X is defined as \(f_X(x) = \frac{1}{b - a} \) so, we can write it as \(f_X ( x) =\begin{cases} \frac{1}{5},\quad 4≤ x ≤ 9 \\ 0, \quad otherwise \\ \end{cases}\).
We have to determine the probability density function \(f_Y(y)\). For this first we have to calculate the cumulative distribution function for f(x) is written as \(F_X(x) = \int_{4}^{x} f(x) dx \)
\(= \int_{4}^{x} \frac{1}{5} dx \)
\(= \frac{1}{5} [ x]_{4}^{x} \)
\(F_X(x) = \frac{x - 4}{5}\)
Now, we have, \( Y = \sqrt{X}\)
when X = 4 => Y = 2 and X = 9 => Y = 3
Also, X = Y²
Differentiating X = Y² with respect to Y
=> dX = 2Y dY
=> dX/dY = 2Y
Now, pdf of Y is written as \(f_Y(y) = f_X(x)|\frac{dX}{dY}| \)
\( = \frac{ 1}{5} × 2y\)
\(= \frac{ 2y}{5}\)
So, \(f_Y( y) =\begin{cases} \frac{2y}{5},\quad 2≤ x ≤ 3 \\ 0, \quad \: otherwise \ \ \end{cases}\). Hence, required value is \(f_Y( y) =\begin{cases} \frac{2y}{5},\quad 2≤ x ≤ 3 \\ 0, \quad \: otherwise \ \ \end{cases}\).
For more information about uniform distribution, visit :
https://brainly.com/question/31293679
#SPJ4
Complete question:
The above figure complete the question.
![Suppose a continuous random variable X is uniformly distributed on the interval [4,9]. able Y distributed?](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/nxh50RPDAVKvcQ3eaCbJnTUKucKYFdYM.jpeg)
Solve the inequality. 22−2x<38 Which answer represents the solution set?
Answers
Answer:
x >-8
Step-by-step explanation:
22−2x<38
Subtract 22 from each side
22-22−2x<38-22
-2x < 16
Divide each side by -2, remembering to flip the inequality
-2x/-2 > 16/-2
x >-8
If desalinated water costs $ 2100 per acre-foot, how much does desalinated water cost per liter? ΑΣφ ? $/L Request Answer Submit Part B How much would it cost one household per day if it were the only source of water?
Answers
The cost of desalinated water is approximately $0.00513 per liter.
To calculate the cost of desalinated water per liter, we need to convert the cost from acre-feet to liters and then divide it by the total volume.
1 acre-foot is equal to 1233.48 cubic meters or 1,233,480 liters. Therefore, if desalinated water costs $2100 per acre-foot, the cost per liter can be calculated as follows:
Cost per liter = Cost per acre-foot / Volume in liters
Cost per liter = $2100 / 1,233,480 liters
Cost per liter ≈ $0.00513
For Part B, we need additional information about the water consumption of the household per day to calculate the cost.
For more questions like Water click the link below:
https://brainly.com/question/1992092
#SPJ11
given that the absolute value of the difference of the two roots of $ax^2 + 5x - 3 = 0$ is $\frac{\sqrt{61}}{3}$, and $a$ is positive, what is the value of $a$?
Answers
The value of "a" is approximately 1.83 given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive.
We are given that the absolute value of the difference between the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive. We need to find the value of "a".
Let the two roots of the equation be r1 and r2, where r1 is not equal to r2. Then, we have:
|r1 - r2| = √(61) / 3
The sum of the roots of the quadratic equation is given by r1 + r2 = -5 / a, and the product of the roots is given by r1 × r2 = -3 / a.
We can express the difference between the roots in terms of the sum and product of the roots as follows:
r1 - r2 = √((r1 + r2)² - 4r1r2)
Substituting the expressions we obtained earlier, we have:
r1 - r2 = √(((-5 / a)²) + (4 × (3 / a)))
Simplifying, we get:
r1 - r2 = √((25 / a²) + (12 / a))
Taking the absolute value of both sides, we get:
|r1 - r2| = √((25 / a²) + (12 / a))
Comparing this with the given expression |r1 - r2| = √(61) / 3, we get:
√((25 / a²) + (12 / a)) = √(61) / 3
Squaring both sides and simplifying, we get:
25 / a² + 12 / a - 61 / 9 = 0
Multiplying both sides by 9a², we get:
225 + 108a - 61a² = 0
Solving this quadratic equation for "a", we get:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61)
Since "a" must be positive, we take the positive root:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61) ≈ 1.83
Therefore, the value of "a" is approximately 1.83.
Learn more about absolute value at
https://brainly.com/question/1301718
#SPJ4
The question is -
Given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive, what is the value of "a"?
match each verbal description to its equivelent function rule as applied to the given function below.

Answers
The parent function is f(x) = 7x + 5.
So let's find the equation for each transformation:
a) The function f reflected about the y-axis and translated 3 units left.
A reflection about the y-axis can be calculated just changing the sign of the variable x:
\(f(x)=7x+5\to f^{\prime}(x)=7\cdot(-x)+5=-7x+5\)Now, in order to translate 3 units left, we just need to add 3 units to the x-value:
\(\begin{gathered} f^{\prime}(x)=-7x+5\to g(x)=-7(x+3)+5 \\ g(x)=-7x-21+5 \\ g(x)=-7x-16 \end{gathered}\)b) The function f stretched vertically by a factor of 3 and translated up by 2 units.
In order to stretch up the function, we multiply the whole function by the factor:
\(\begin{gathered} f(x)=7x+5\to f^{\prime}(x)=3\cdot(7x+5) \\ f^{\prime}(x)=21x+15 \end{gathered}\)Then, to translated 2 units up, we add 2 units of the function:
\(\begin{gathered} f^{\prime}(x)=21x+15\to g(x)=21x+15+2 \\ g(x)=21x+17 \end{gathered}\)c) The function f translated 2 units down and 3 units right.
To do a translation of 2 units down, we subtract 2 units of the function, and to translate 3 units right, we subtract 3 units from the value of x:
\(\begin{gathered} f(x)=7x+5\to f^{\prime}(x)=7x+5-2 \\ f^{\prime}(x)=7x+3 \\ \\ f^{\prime}(x)=7x+3\to g(x)=7\cdot(x-3)+3 \\ g(x)=7x-21+3 \\ g(x)=7x-18 \end{gathered}\)d) The function f stretched vertically by a factor of 2 and translated down by 3 units.
In order to stretch up the function, we multiply the whole function by the factor:
\(\begin{gathered} f(x)=7x+5\to f^{\prime}(x)=2\cdot(7x+5) \\ f^{\prime}(x)=14x+10 \end{gathered}\)Then, to translated 3 units down, we subtract 3 units of the function:
\(\begin{gathered} f^{\prime}(x)=14x+10\to g(x)=14x+10-3 \\ g(x)=14x+7 \end{gathered}\)Use the given scale factor in the side length of the scale drawing to determine the side links of the real object
Answers
Answer:
A. side a is 7 inches long, side b is 6 inches long,and side c is 3 inches long
Step-by-step explanation:
Here is the complete question. Please find attached a diagram showing the scaled and real drawing
Use the given scale factor and the side lengths of the scale drawing to determine the side lengths of the real object
A. side a is 7 inches long, side b is 6 inches long,and side c is 3 inches long
B. side a is 30 inches long, side b is 25 inches long, and side c is 20 inches long
C. side a is 40 inches long, side b is 35 inches long,and side c is 20 inches long
D. side a is 175 inches long,side b is 150 inches long, and side c is inches long
A scale drawing is a reduced form in terms of dimensions of an original image / building / object
the scale drawing is usually reduced at a constant dimension
scale of the drawing = original dimensions / dimensions of the scale drawing
The scaled drawing is an enlarged image of the original triangle.
It is enlarged at a ratio of 5:1
original dimensions
a = 35/5 = 7
b = 30 / 5 = 6
c = 15/5 = 3

What is the following expression?
12-3×(8-5)
will give brainliest :)
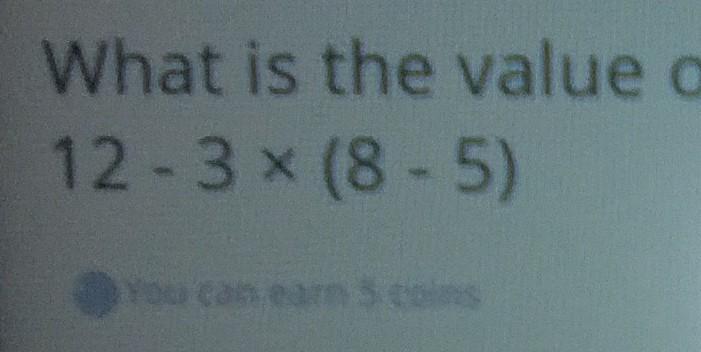
Answers
I believe that the following expression is 3. I hope that's right ♡
Explanation:
What linear expression would you need to add to (-6x+3) to have a sum of -x?
Answers
Answer:
5x-3
Step-by-step explanation:
(-6x+3)+(5x-3)
-6x+3+5x-3
-x
The value that should be added to the expression (-6x+3) is (5x-3) to get the value -x.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
The given expression is (-6x+3). The value to be added to the expression to get the value of -x is calculated as,
E = (-6x+3)+(5x-3)
E = -6x+3+5x-3
E = -x
Therefore, the value that should be added to the expression (-6x+3) is (5x-3) to get the value -x.
To know more about an expression follow
https://brainly.com/question/25968875
#SPJ5
How do you graph a quadratic form?
Answers
The Graph of quadratic functions gives parabolas that are U-shaped, and wide or narrow depending upon the coefficients of the function.
The graph of quadratic functions is a technique to study the nature of the quadratic functions graphically. The shape of the parabola is determined by the coefficient 'a' of the quadratic function f(x) = ax2 + bx + c, where a, b, c are real numbers and a ≠ 0.
the vertex of a quadratic function is. \(f(x)=a(x-h)^2+k, where (h,k)\) is the vertex of parabola. When a>0 then function will be open upward if a<0 then function will be opens downward.
Steps to plot graph of quadratic function.
a\(x^2\) is imply a vertical scaling of the parabola, if a<0 the parabola will also flip its mouth from the positive to negative side.
\(a(x+\frac{b}{2a} )^2\) This is a horizontal shift of magnitude |\(\frac{b}{2a}\)| units. The direction of the shift will be decided by the sign of b/2a. The new vertex of the parabola will be at (-b/2a,0).
This transformation is a vertical shift of magnitude |\(\frac{D}{4a}\)| units. The direction of the shift will be decided by the sign of \(\frac{D}{4a}\). The final vertex of the parabola will be at (\(\frac{-b}{2a} ,\frac{-D}{4a}\)).
So, The Graph of quadratic functions gives parabolas that are U-shaped, and wide or narrow depending upon the coefficients of the function.
Learn more about quadratic function.
https://brainly.com/question/29775037
#SPJ4
Consider the probability distribution of the random variable X
X P(X)
0 0.1
1 0.2
2 0.3
3 ?
a. Find the missing (?) probability value
b. Find E(X).
c. Find Var(X) and x.
d. If Z = 1 + 2/3X, find E(Z), Var(Z) and z.
Answers
a. The missing probability value is 0.4.
b. E(X) = 1.4.
c. Var(X) = 0.56 and σx = 0.75.
d. E(Z) = 2.27, Var(Z) = 2.56, and σz = 1.60.
The given probability distribution of the random variable X shows the probabilities associated with each possible outcome. To find the missing probability value, we know that the sum of all probabilities must equal 1. Therefore, the missing probability can be calculated by subtracting the sum of the probabilities already given from 1. In this case, 0.1 + 0.2 + 0.3 = 0.6, so the missing probability value is 1 - 0.6 = 0.4.
To find the expected value or mean of X (E(X)), we multiply each value of X by its corresponding probability and then sum up the results. In this case, (0 * 0.1) + (1 * 0.2) + (2 * 0.3) + (3 * 0.4) = 0.4 + 0.2 + 0.6 + 1.2 = 1.4.
To calculate the variance (Var(X)) of X, we use the formula: Var(X) = Σ[(X - E(X))^2 * P(X)], where Σ denotes the sum over all values of X. The standard deviation (σx) is the square root of the variance. Using this formula, we find Var(X) = [(0 - 1.4)² * 0.1] + [(1 - 1.4)^2 * 0.2] + [(2 - 1.4)² * 0.3] + [(3 - 1.4)² * 0.4] = 0.56. Taking the square root, we get σx = √(0.56) ≈ 0.75.
Now, let's consider the new random variable Z = 1 + (2/3)X. To find E(Z), we substitute the values of X into the formula and calculate the expected value. E(Z) = 1 + (2/3)E(X) = 1 + (2/3) * 1.4 = 2.27.
To calculate Var(Z), we use the formula Var(Z) = (2/3)² * Var(X). Substituting the known values, Var(Z) = (2/3)² * 0.56 = 2.56.
Finally, the standard deviation of Z (σz) is the square root of Var(Z). Therefore, σz = √(2.56) = 1.60.
Learn more about probability value
brainly.com/question/30897652
#SPJ11
The truth table represents statements p, q, and r.
p q r p ∧ q p ∧ r
A T T T T T
B T T F T F
C T F T F T
D T F F F F
E F T T F F
F F T F F F
G F F T F F
H F F F F F
Which rows represent when (p ∧ q) ∨ (p ∧ r) is true?
A and B
A, B, and C
B and E
Answers
Answer:
A, B, and C
Step-by-step explanation:
EDGE unit test 2020
The rows that stands for when (p ∧ q) ∨ (p ∧ r) is true is row A, B, and C. Check more about Truth table below
What is a truth table?The truth table is known to be a table that depicts the real value of any kind of compound statement.
Note that for every truth-value of a statements there is a similar table depicting the value of the output for all of the value of all of the input and as such, rows that stands for when (p ∧ q) ∨ (p ∧ r) is true is row A, B, and C.
Learn more about Truth table from
https://brainly.com/question/14458200
#SPJ2
if calls to your cell phone are a poisson process with a constant rate of 2 calls per hour, what is the probability that, if you forget to turn your phone off during a 1.5-hour movie, your phone rings during that time? how many calls do you expect to get during that movie?
Answers
we can expect to receive approximately 3 phone calls during the 1.5-hour movie, on average.
The probability of your phone ringing during a 1.5-hour movie can be calculated using the Poisson distribution formula:
P(X = k) = (e^-λ * λ^k) / k!
Where X is the number of phone calls, λ is the average rate of calls per unit time (in this case, 2 calls per hour), and k is the number of calls during the 1.5-hour period.
So, for k = 0 (no calls), the probability is: P(X = 0) = (e^-2 * 2^0) / 0! = e^-2 ≈ 0.1353
Therefore, the probability that your phone rings at least once during the movie is: P(X ≥ 1) = 1 - P(X = 0) = 1 - e^-2 ≈ 0.8647
To calculate the expected number of calls during the movie, we use the formula: E(X) = λ * t
Where t is the duration of the period (1.5 hours in this case). So, the expected number of calls during the movie is: E(X) = 2 * 1.5 = 3
Therefore, we can expect to receive approximately 3 phone calls during the 1.5-hour movie, on average.
To know more about probability click here
brainly.com/question/15124899
#SPJ11
The ray y=x,x>=0 contains the origin and all points in the coordinate system whose bearing is 45\deg . Determine the equation of a ray consisting of the origin and all points whose bearing is 60\deg .
Answers
The equation of the ray consisting of the origin (0, 0) and all points whose bearing is 60° is y = √3x.
To determine the equation of the ray consisting of the origin and all points whose bearing is 60°, we can use the slope-intercept form of a line, which is y = mx.
Given that the ray passes through the origin (0, 0), we know that the y-intercept is 0.
The bearing of 60° corresponds to a slope of tan(60°).
Let's calculate the slope:
slope = tan(60°) = √3
Therefore, the equation of the ray can be written as:
y = √3x
Hence, the equation of the ray consisting of the origin (0, 0) and all points whose bearing is 60° is y = √3x.
To learn more about ray
https://brainly.com/question/31176412
#SPJ11
Is -6.5555 a rational or irrational number?
Answers
Answer:
Rational
hope this helps
have a good day :)
Step-by-step explanation:
Answer:
Rational.
Step-by-step explanation:
Rational numbers are the numbers that can be expressed in the form of a ratio.
I lowered the points because people were stealing them.

Answers
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
Domain ~
\( - 6 \leqslant x \leqslant - 1\)Range ~
\( - 5 \leqslant x \leqslant - 3\)what's the place value of the 1 in 352.01
Answers
Answer:
100ths place
Step-by-step explanation:
You want to be able to withdraw the specified amount periodically from a payout annuity with the given terms. Find how much the account needs to hold to make this possible. Round your answer to the nearest dollar. Regular withdrawal: Interest rate: Frequency Time: $3200 4. 5% quarterly 18 years Account balance: $â
Answers
To withdraw $3,200 quarterly at an interest rate of 4.5% for 18 years, the account balance needs to be approximately $178,311. This is calculated using the formula for the present value of an annuity, where the payment, interest rate, time period, and compounding frequency are considered.
To find the account balance needed, we need to use the present value of an annuity formula.
Convert the annual interest rate to a quarterly rate: 4.5% / 4 = 1.125%
Convert the number of years to the number of quarters: 18 years * 4 quarters per year = 72 quarters
Calculate the present value of the annuity using the formula:
PV = PMT * (1 - (1 + r)⁻ⁿ) / r
where PV is the present value, PMT is the regular withdrawal amount, r is the quarterly interest rate, and n is the number of quarters.
Plugging in the values, we get
PV = 3200 * (1 - (1 + 0.01125)⁻⁷²) / 0.01125
= 3200 * (1 - 0.2717) / 0.01125
= 178,311.11
Round the answer to the nearest dollar: $178,311
Therefore, the account needs to hold $178,311 to make regular withdrawals of $3200 per quarter for 18 years at a quarterly interest rate of 4.5%.
To know more about interest rate:
https://brainly.com/question/15089941
#SPJ4
What is the area of triangle ABC if a = 7, c = 11, and B = 55°?
Round the answer to the nearest hundredth.
Answers
The area of the triangle is 31.54 square units
How to determine the area of the triangleFrom the question, we have the following parameters that can be used in our computation:
We have the following values
a = 7 units
c = 11 units
B = 55 degrees
The area of the triangle is calculated using the following area formula
Area = 1/2absin(C)
Substitute the known values in the above equation, so, we have the following representation
Area = 1/2 * 7 * 11 * sin(55 degrees)
Evaluate
Area = 31.54
Hence, the area is 31.54 square units
Read more about area at
brainly.com/question/25292087
#SPJ1
determine whether the relation defines y as a function of x. Guve the domain.

Answers
Answer
Explanation
Given:
\(y=-\frac{5}{x}\)To determine whether the relation defines y as a function of x, we get the domain first.
Based on the given relation, when we plug in x=0, the value would be undefined. So the function domain is x<0 or x>0.
Hence, the interval notation is:
\((-\infty,0)\cup(0,-\infty)\)We can use vertical line test to determine if it is a function as shown in the graph below:
As we can see, there's only one point of intersection so the relation defines y as a function of x. Therefore, the answer is:
Function; domain
\((-\infty,0)\cup(0,-\infty)\)
25^2/5 using the root symbol
Answers
Answer:
5 outside of the square root symbol and 625 on the inside
Develop a full regression model based on all the predictor variables indicated. Choose the right model equation below
A. Assessed Value = 246.42+43.94*(Size) + 15.69*(Fireplace Coded)+8.25*(Bedrooms) B. Asking Price = 246.42+43.94*(Size) + 15.69*(Fireplace Coded)+8.25*(Bedrooms)
C. Assessed Value = 246.42+43.94*(Size) + 15.69*(Fireplace Coded)+0.9677*(Bathrooms) D. Assessed Value = 244.4325 + 43.5532*(Size)+ 8.1910*(Bedrooms)+ 0.9677*(Bathrooms)
Q2. A review of the t-test on the significance of individual independent variable suggests that, based on the p-values
A. Only one of the independent variable possibly needs to be retained B. Two of the independent variables possibly needs to be retained C. None of the independent variables could be retained D. Three of the independent variables could be retained
Q3:
Choose the right option below. Based on the full regression model involving all of the independent variables
A. VIF for Size = 2.336, VIF for Fireplace = 1.121, VIF for bedrooms = 1.979
B. VIF for Size = 5.3352, VIF for Fireplace = 10.1873, VIF for bedrooms = 2.7885
C. VIF for Fireplace = 1.1873, VIF for bedrooms = 1.9885
D. None of the above
Q4: Based on VIF values, there is concern for collinearity in this dataset
A. True B. False
Q5:
Based on the normal probability plot, the normality assumption seems to be met
A. True
B. False
Q:7: Based on conducting residual analysis the model seems
Group of answer choices
Adequate
Inadequate
Violates Independence Assumption
Not enough information to assess the LINE assumptions
Answers
Q.2: A review of the t-test on the significance of individual independent variable suggests that, based on the p-values. None of the independent variables could be retained. This is because if the p-value is high, it means the significance is low.
Q3: Choose the right option below. Based on the full regression model involving all of the independent variables. VIF for Size = 5.3352, VIF for Fireplace = 10.1873, VIF for bedrooms = 2.7885.
Q.4: Based on VIF values, there is concern for collinearity in this dataset. True
Q5: Based on the normal probability plot, the normality assumption seems to be met. True
Q7: Based on conducting residual analysis the model seems. Adequate.
Learn more about independent variable at
https://brainly.com/question/7228371
#SPJ11
richard klein works as auto mechanic and earns the following commission rates 3.00 percent for oil changes 5.00 percent for tune ups and 6.25 percent on auto parts sales he is guaranteed a minimum salary of $2,450.00 per month last month he brought in $2,500.00 in oil changes $4,500.00 in tune ups and sold $28,200.00 in parts what is his gross pay for the month
Answers
Answer:
His gross pay for the month is $4,509.50
Step-by-step explanation:
The commission Richard Klein earns for oil change = 3.00%
The commission he earns for tune ups = 5.00%
The commission he earns for auto parts sales = 6.25%
The minimum salary he is guaranteed = $2,450.00
The amount he brought in last month includes;
1) $2,500.00 in oil changes
2) $4,500 in tune ups
3) Sold $28,200.00 in parts
The amount he earns last month in commission are;
3/100 × 2,500 = 75 in oil changes
5/100 × 4,500 = 225 in tune ups
6.25/100 × 28,200 = 1762.5 in parts sold
The total commission = 72 + 225 + 1762.5 = 2,059.5
∴ The total commission = $2,059.5
The amount he makes as salary = $2,450.00
Richard Klein's gross pay for the month = His total pay for the month
Therefore;
Richard Klein's gross pay for the month = $2,059.5 + $2,450 = $4,509.5
Which of the following expressions correctly determines that x is greater than 10 and less than 20?
a. 10 < x < 20
b. ( 1 0 < x < 20)
c. 10 < x & & x < 20
d. 10 < x I I x < 20
Answers
Option d is not correct as it uses "II" which is not a commonly used symbol to indicate less than and greater than.
What is the correct expression to indicate?The correct expression to indicate that x is greater than 10 and less than 20 is:
a. 10 < x < 20
This is read as "10 is less than x, and x is less than 20." The symbols "<" and ">" indicate "less than" and "greater than," respectively.
Option b is not correct as it uses parentheses instead of the less than/greater than symbols.
Option c is not correct as it uses "&" and "&&" which are not commonly used symbols to indicate less than and greater than.
Option d is not correct as it uses "II" which is not a commonly used symbol to indicate less than and greater than.
Learn more about symbol
brainly.com/question/11490241
#SPJ11
2.) The corresponding sides of two similar parallelograms measure 4 and 12. If the area of the larger parallelogram is 72, what is the area of the smaller parallelogram?
Answers
The area of the smaller parallelogram will be 8 square units.
What is parallelogram?The parallelogram is a quadrilateral whose two opposite sides are parallel to each other.
In the question the two corresponding sides of the two similar parallelogram are 4 and 12 so the ratio of the larger and the smaller parallelogram will be 3:1
Now the area of the smaller parallelogram will be calculated as
\((\dfrac{3}{1})^2=\dfrac{72}{A_s}\)
\(A_s=\dfrac{72}{9}=8\)
Hence the area of the smaller parallelogram will be 8 square units.
To know more about Parallelogram follow
https://brainly.com/question/970600
#SPJ1