If y=-1 is a zero of the polynomial q (y) = 4y³+ ky² - y -1, then find the vaLue of k
Answers
Answer:
Step-by-step explanation:
Since zero of a polynomial function is a value of the variable at which the function's value is 0, 0=4(-1)^3+k(-1)^2-(-1)-1, for the given polynomial q(y)=4y^3+ky^2-y-1
simplifying the above gives: 0= -4+k+0
k=4
Related Questions
A company manufacturing bike helmets wants to estimate the proportion p of helmets with a certain type of flaw. They decide to keep inspecting helmets until they find r = 5 flawed ones. Let X denote the number of helmets that were not flawed among those examined.
(a) Write the log-likelihood function and find the MLE of p. (Hint. What is the distribution of X + 5?)
(b) Find the method of moments estimator of p.
(c) Find the model-based estimator of the variance of X and the model-based estimator of P(X = 0). (Hint. Compute the true value as a function of model parameter p and them plug in the estimator
Answers
(a) The log-likelihood function log L(p) = const + 5 log p + (n-5) log (1-p) and MLE of p is 5/n. (b) The method of moments estimator of p is (n-r)/n. (c) The model-based estimator of P(X = 0), P_hat(X=0) = \((1 - 5/n)^n\)
(a) The number of flawed helmets, Y, follows a binomial distribution with parameters n (the number of helmets inspected) and p (the proportion of flawed helmets). Thus, the number of helmets that were not flawed, X = n - Y, also follows a binomial distribution with parameters n and 1 - p. Since we know that r = 5 flawed helmets were found, we can write:
Y ~ Binomial(n, p), with probability mass function (PMF) f(Y) = (n choose Y) \(p^Y (1-p)^{(n-Y)\)
X = n - Y ~ Binomial(n, 1-p), with PMF f(X) = (n choose X) \((1-p)^X p^{(n-X)\)
We want to find the MLE of p based on the observed value r = 5. The likelihood function is:
L(p) = f(Y=5) = (n choose 5) \(p^5 (1-p)^{(n-5)\)
Taking the logarithm of L(p), we get:
log L(p) = const + 5 log p + (n-5) log (1-p)
To find the MLE of p, we differentiate log L(p) with respect to p and set the derivative equal to 0:
d/dp log L(p) = 5/p - (n-5)/(1-p) = 0
Solving for p, we get:
p = 5/n
Thus, the MLE of p is 5/n.
(b) The method of moments estimator of p is obtained by equating the sample mean (which is an estimate of the population mean) to the theoretical mean. The mean of X is n(1-p), so we have:
n(1-p) = n - r
Solving for p, we get:
p = (n-r)/n
Thus, the method of moments estimator of p is (n-r)/n.
(c) Since X ~ Binomial(n, 1-p), the mean and variance of X are:
E(X) = n(1-p)
Var(X) = n(1-p)p
Plugging in the MLE of p from part (a), we get:
E(X) = n - 5
Var(X) = (n/6) * (1 - 5/n) * 5/n
The model-based estimator of the variance of X is the plug-in estimator, which replaces the unknown parameter p with its MLE:
Var_hat(X) = (n/6) * (1 - 5/n) * 5/n
To find the model-based estimator of P(X = 0), we use the PMF of X:
P(X = 0) = (n choose 0) \((1-p)^n = (1-p)^n\)
Plugging in the MLE of p from part (a), we get:
P_hat(X=0) = \((1 - 5/n)^n\)
For more such questions on Moments estimator.
https://brainly.com/question/30435928#
#SPJ11
Which of the following are solutions to the equation below?
Check all that apply.
x2 + 6x + 9 = 20
A. x= 13 + 20
B. X = -2.75 +3
C. X = 2.5+ 3
D. X = -1/5 + 20
E. X = 2.5 - 3
F. x = -24/5-3
Answers
I need help finding the distance on here, I got the wrong answer when tried please help thank you

Answers
The distance of person A from the hot air balloon is approximately 780m to the nearest whole number using the trigonometric ratios of tangent and cosine
What is trigonometric ratios?The trigonometric ratios is concerned with the relationship of an angle of a right-angled triangle to ratios of two side lengths.
The basic trigonometric ratios includes;
sine, cosine and tangent.
Considering the right triangle ∆BDC, angle D can be derived as:
tan BDC = 200/384 {opposite/adjacent}
angle BDC = tan⁻¹(200/384)
angle BDC = 27.5°
For right triangle ∆ADC;
angle ADC = 33 + 27.5 = 60.5°
The distance of person A from the hot air balloon is the length AD and can be calculated as follows;
cos60.5 = 384/AD {adjacent/hypotenuse}
AD = 384/cos60.5
AD = 779.8165
Therefore, the distance of person A from the hot air balloon is approximately 780m to the nearest whole number using the trigonometric ratios of tangent and cosine
Read more about trigonometric ratios here: https://brainly.com/question/3457795
#SPJ1
Solve the simultaneous equation 24n+9m=8 and 3n-2m=6
Answers
Answer:
We can solve the simultaneous equation 24n + 9m = 8 and 3n - 2m = 6 by using the elimination method.
First, we need to multiply the second equation by 3 to eliminate n:
24n + 9m = 8
(3n - 2m) × 3 = 6 × 3
9n - 6m = 18
Now we have two equations with the same n coefficient, so we can subtract the second equation from the first to eliminate n:
24n + 9m = 8
-(9n - 6m = 18)
-----------------
15n + 15m = -10
We can simplify this equation by dividing both sides by 5:
3n + 3m = -2
Now we have two equations with the same m coefficient, so we can subtract the second equation from the first to eliminate m:
24n + 9m = 8
-(3n + 3m = -2)
----------------
21n + 6m = 10
We can simplify this equation by dividing both sides by 3:
7n + 2m = 10/3
Now we have two equations with only one variable, so we can solve for one variable and substitute the value into one of the original equations to solve for the other variable:
7n + 2m = 10/3
2m = 10/3 - 7n
m = (10/3 - 7n)/2
Substitute this expression for m into the first equation:
24n + 9m = 8
24n + 9[(10/3 - 7n)/2] = 8
24n + (30/2 - 63n/2)/2 = 8
24n + 15 - 63n/4 = 8
24n - 63n/4 = 8 - 15
(96n - 63n)/4 = -7
33n/4 = -7
n = -28/33
Substitute this value of n into the second equation:
3n - 2m = 6
3(-28/33) - 2m = 6
-28/11 + 2m/11 = 2
2m/11 = 2 + 28/11
2m/11 = 50/11
Answer:
n = 14 / 15
m = -8 / 5
Step-by-step explanation:
24n + 9m = 8 ------- (1) x 2
3n - 2m = 6 -----------(2) x 9
48n + 18m = 16 ------- (3)
27n - 18m = 54 --------(4)
Adding two eqn , we get ;
______________
75n = 70
n = 14 / 15
Putting value of n in eqn (2) , we get ;
14 / 5 - 2m = 6
2m = 14 / 5 - 6
2m = -16 / 5
m = -8 / 5
suppose you have calculated a two-way anova where the interaction was not significant. how should you next proceed?
Answers
The connection test is performed prior to making any ends in view of the tests for the primary impacts. The effect of one factor on the population mean when two factors interact is determined by the specific value or level of the other factor.
Before drawing any conclusions based on the tests for the main effects, the interaction test is carried out. The effect of one factor on the population mean when two factors interact is determined by the specific value or level of the other factor.
There may be an interaction if the plot's lines don't line up in the same direction. A collaboration demonstrates that the method for the Y information at the levels of the main X variable are different at each level of the second X variable. The interaction's strength increases with the number of nonparallel lines.
To learn more about Interaction test here
https://brainly.com/question/29633075
#SPJ4
A kangaroo chae a rabbit that tart 150 feet ahead of the kangaroo. For every 12-foot leap of the kangaroo, the rabbit leap 7 feet. How many leap would the kangaroo have to make to catch up to the rabbit?
Answers
Rabbit leaps two feet. Kangaroo leaps sixteen feet. sEight time as far as the rabbit, the kangaroo jumps.
What is unitary method?The unitary technique involves first determining the value of a single unit, followed by the value of the necessary number of units. what kinds of values and units
Let's say you go to the store to buy six apples.
You are informed by the shopkeeper that he is offering 10 apples for Rs 100. In this instance, the value and the units are the price of the apples. Recognizing the units and values is crucial when using the unitary technique to a problem.
Always write the items that need to be computed on the right side and the things that are known on the left side to simplify things.
We are aware of the quantity of apples and the amount of money in the aforesaid problem.
According to our question-
A bunny leaps two feet. The kangaroo leaps 16 feet. The kangaroo leaps eight times farther than the rabbit.
learn more about unitary method click here:
brainly.com/question/24587372
#SPJ4
Travis bought 60 cans of soda for a party. He bought 24 cans of diet cola and 36 cans
of regular cola. What percent of the soda that Travis bought is diet cola?
PLEASE EXPLAIN!
Answers
The percentage of diet cola Travis bought is 60%
PercentageA percentage is a number or ratio that can be expressed as a fraction of 100. If we have to calculate percent of a number, divide the number by the whole and multiply by 100. Hence, the percentage means, a part per hundred. The word per cent means per 100. It is represented by the symbol “%”.
Using the data given;
Total = 60 diet cola = 24regular cola = 36The percentage of diet cola bought is calculated as;
Percentage of diet cola = (diet cola / total cans) * 100
Percentage of diet cola = (24 / 60) * 100
Percentage of diet cola = 40%
Learn more on percentage here;
https://brainly.com/question/24877689
#SPJ1
Which expression is equivalent to the question?

Answers
Answer:the third one I suppose
Step-by-step explanation:
If a sample of 64 golfers is taken from a population of 190 golfers, the
sample mean, X, is the mean of how many golfers' scores?
A. 64
B. Neither 64 nor 190
C. 190
D. Both 64 and 190
SUBMIT
Answers
Explanation:
Its either tricky or I’m thinkin too hard on it, but I’m seeing that 64 golfers were TAKEN OUT the population of 190 golfers, so it can’t be either.
Answer:
64
Step-by-step explanation:
ITSSSS 64!!
Question: which number represents the following 8 degrees warmer today than monday answers: -7, 0, 7, 14
Answers
The number that represents 8 degrees warmer today than Monday is 0.
To find this, we can subtract 8 from the number that represents Monday's temperature.
Since Monday's temperature is not provided in the question, we cannot determine the exact number. However, out of the given options (-7, 0, 7, 14), the only number that is 8 degrees warmer than any other number is 0.
So, 0 represents the number that is 8 degrees warmer today than Monday.
8 degrees and Monday : https://brainly.com/question/30199233
#SPJ11
Mr tuyen uses 5/8 of a tank of gas each week to drive to and from his job. How many tanks of gas does Mr.tuyen
used in five weeks write your answer two different ways.
Answers
Mr. Tuyen uses 25/8 or 3 1/8 (or 3 1/64) tanks of gas in five weeks.
As per the question,
Multiply the amount of gas used in one week (5/8 tank) by the number of weeks (5):
5/8 x 5 = 25/8 tanks of gas.
Simplify the fraction 25/8 by dividing the numerator and denominator by 8: 25/8 ÷ 8/8 = 25/64.
25/64 is an improper fraction, so we can convert it to a mixed number:
3 1/64 tanks of gas.
Alternative method:
In one week, Mr. Tuyen uses 5/8 of a tank of gas.
In five weeks, he uses 5/8 x 5 = 25/8 tanks of gas.
25/8 is an improper fraction, so we can convert it to a mixed number: 3 1/8 tanks of gas.
Therefore, Mr. Tuyen uses 25/8 or 3 1/8 (or 3 1/64) tanks of gas in five weeks.
Learn more about the fraction here:
brainly.com/question/10354322
#SPJ1
The weekly sales of an album have increased since it was first sold at a music store 6 weeks ago. The linear regression equation describing the change is y=1.9x+13.3 , where x represents the week and y represents the number of albums sold per week. Round the residual value to the nearest integer and then construct a residual plot of the data.
Answers
The residual value to the nearest integer and then construct the residual plot of the data will be 25.
What is a linear equation?A connection between a number of variables results in a linear model when a graph is displayed. The variable will have a degree of one.
The linear equation is given as,
y = mx + c
Where m is the slope of the line and c is the y-intercept of the line.
Since an album went on sale for the first time at a music retailer six weeks ago, its weekly sales have climbed. The change is described by the linear regression equation y=1.9x+13.3, where x is the week and y is the number of albums sold each week.
The residual value is given as,
y = 1.9(6) + 13.3
y = 11.4 + 13.3
y = 24.7
y ≅ 25
The residual value to the nearest integer and then construct the residual plot of the data will be 25.
More about the linear equation link is given below.
https://brainly.com/question/11897796
#SPJ1
-7x + 13 > 41
The Solution to the Inequality is ________. A graph of the solution should have __________ and be shaded to the _____.
Fill on the Blanks
Answers
Answer:
x>4
Step-by-step explanation:
-7x+13>41
-13 -13
-7x>28
/-7 /-7
x>4
Answer:
x < -4
a filled circle on -4
should be shaded to the left
Step-by-step explanation:
The seventh grade class is putting on a verity shell to raise money it cost 1700 to rent the banquet hall That they are going to use. If they charge for $55 for each ticket, how many tickets do they need to sell in order to raise at least $2000 write an inequality that represents the situation.how many tickets do they need to sell?
Answers
Answer:
g
Step-by-step explanation:
Write 4 over 8 as a percent and as a decimal. this is so easy I know
Answers
Answer:
As a decimal 0.5
as a percentage 50%
\(\bf \sqrt{49}\times \sqrt{49}\)
Answers
\( = 49\)
Step-by-step explanation:
\( \sqrt{49} \times \sqrt{49} \)
When a square root of an expression is multiplied by itself, the result is that expression\( = 49\)
hope it helps
Answer:
\(\sf\longmapsto \: 49\)
Step-by-step explanation:
\(\sf\longmapsto \sqrt{49} \times \sqrt{49} \)
\(\sf\longmapsto \: {49} \)
Study the outcrops of the Mesozoic (green) and Cenozoic (yellow) rocks in the map area. What structures are indicated by these map patterns
Answers
The structures indicated by the map patterns of Mesozoic (green) and Cenozoic (yellow) rocks can provide insights into the geological history and tectonic activity of the area.
The presence of linear or curvilinear patterns in the map may suggest the occurrence of faults or fractures in the rocks. Faults are fractures along which rocks on either side have moved relative to each other. These structures can be associated with the movement of tectonic plates and the deformation of the Earth's crust.
Additionally, the map patterns may reveal the presence of folds in the rocks. Folds are bending or flexing of rock layers caused by compressional forces in the Earth's crust. They can result in the formation of anticlines (upward folds) and synclines (downward folds) that can be observed in the map patterns.
The interpretation of the map patterns in terms of specific structures requires careful analysis and additional geological data. Field observations, cross-sections, and geophysical techniques are often employed to gain a better understanding of the geological structures present in the area.
Learn more about curvilinear patterns here:
https://brainly.com/question/28111322
#SPJ11
need help
with 1.9 more especially

Answers
Answer:
1/2 × |AB| × |OE|
Step-by-step explanation:
use the formula for finding the area of a triangle.
PLEASE ANSWER ASP
If the volume of the cylinder is 3000i * n ^ 3 what is the height of the cylinder ? Use 3.14 for and round the answer to the nearest hundredth . r = 10in The length of height=\ in
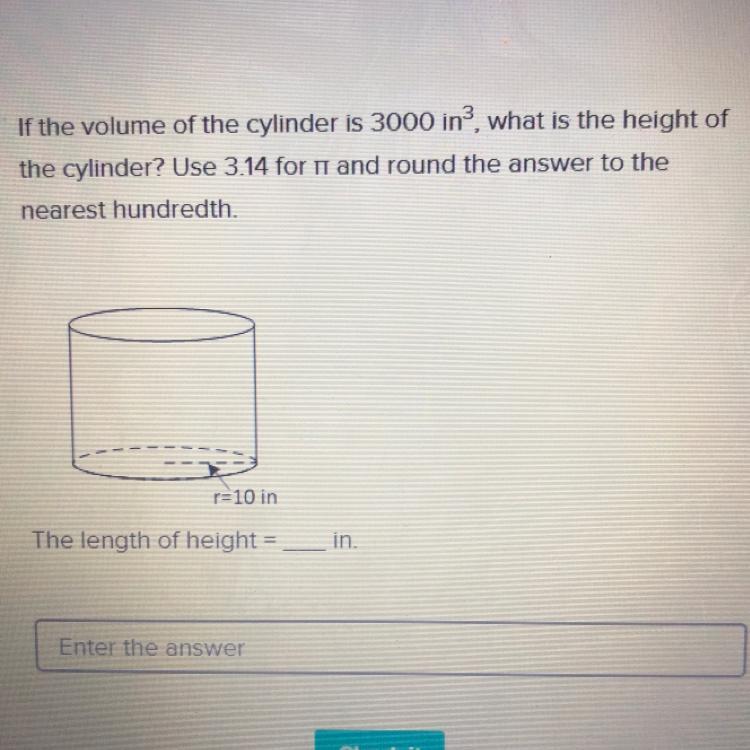
Answers
Answer:
9.55 in
Step-by-step explanation:
First of all we have to find the base area
base area = radius^2 x 3.14 = 10^2 x 3,14 = 100 x 3,14 =314 in^2
the volume of a cylinder is
V = base area x height
so the height is
V/base area
3000 : 314 = 9.55 in
Find a sequence of translations, rotations, and
reflections that transform triangle EFG so that its image
rest on square ABCD to together form a simple drawing
of a house.

Answers
A series of rigid transformation that transform triangle EFG to produce an image that rests on the square ABCD to together form a simple drawing of a house are;
A translation and a counterclockwise rotation
What is a rigid transformation?A rigid transformation is one in which the lengths of corresponding points in the image are preserved.
A sequence of transformations (translations, rotations, and reflections that transform triangle EFG so that its image rest on square ABCD to together form a simple drawing of a house are;
A translation of triangle EFG to the leftA rotation of triangle EFG counterclockwise by an acute angleThe performance of the above transformations will produce the image of the simple drawing of the house consisting of the square base and the triangular top.
Learn more on translation transformation here: https://brainly.com/question/11134096
#SPJ1

Given the differential equation dy dt a) Find the equilibrium solutions for the equation. dy = 0 dx y²-24-8=0 Y = 4,-2 (4-4)(4+21=0 b) Draw a phase line for the equation illustrating where the function y is increasing, decreasing, and label the equilibrium points as a sink, source, or node. for increasing: y & L-00₁-2) 4 (4₁0) Ə for decreasing: ye [-2, 41 c) Draw the slope field using the software I used in the video or similar graphing software then paste it in this document. Where -1 ≤t≤ 1 and -6 ≤ y ≤6 2 224 - + + 4 d) Graph the equilibrium solutions on the slope field. c) Draw the solutions that passes through the point (0,1), (0,-3), and (0,6) = y² - 2y-8
Answers
a) To find the equilibrium solutions of the equation dy/dt = (y² - 24)/(y - 8), we set dy/dt = 0 and solve for y:
(y² - 24)/(y - 8) = 0
The numerator of the fraction is zero when y = ±√24 = ±2√6.
The denominator of the fraction is zero when y = 8.
So, the equilibrium solutions are y = ±2√6 and y = 8.
b) The phase line for the equation can be illustrated as follows:
```
decreasing increasing
| |
V V
-∞ - -2√6 - 8 - 2√6 - ∞
Sink Source
```
The equilibrium point y = -2√6 is a sink, while the equilibrium point y = 8 is a source.
c) Unfortunately, as a text-based AI model, I am unable to generate visual representations or graphs. I recommend using graphing software or online graphing tools to plot the slope field for the given differential equation.
d) To graph the equilibrium solutions on the slope field, you would plot horizontal lines at y = ±2√6 and y = 8, intersecting with the slope field lines.
e) The given equation y² - 2y - 8 can be factored as (y - 4)(y + 2) = 0. This equation has two roots: y = 4 and y = -2.
To draw the solutions that pass through the points (0, 1), (0, -3), and (0, 6), you would plot curves that follow the direction indicated by the slope field and pass through those points.
Learn more about intersecting here:
https://brainly.com/question/12089275
#SPJ11
find the simplified product :

Answers
Answer:
Edge 2021
Step-by-step explanation:
2nd one is C, 3x^4
Quadrilateral LMNO is reflected about the x-axis.
What are the coordinates of the images of vertices L, M, N, and O?
A. L’(2, 5), M’(2, -1), N’(5, -2) and O’(6,-4)
B. L’(-5, 2), M’(-2, -1), N’(-5, -2) and O’(6,-4)
C. L’(2, -5), M’(2, -1), N’(5, -2) and O’(6,-4)
D. L’(2, -5), M’(2, -1), N’(-5, -2) and O’(-6,-4)
(first correct answer gets branleist)

Answers
C.)
L’(2, -5), M’(2, -1), N’(5, -2) and O’(6,-4)
Answer:
c i did the quiz
Step-by-step explanation:
7.
Which of the following is the graph of y = 3x^2 + 6?

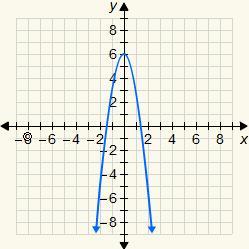

Answers
Answer:
A. graph A
Step-by-step explanation:
Graph the parabola using the direction, vertex, focus, and axis of symmetry.
Direction: Opens Up
Vertex:
( 0 , 6 )
Focus:
( 0 , 73 /12 )
Axis of Symmetry:
x = 0
Directrix:
y = 71 /12
x
y
−
2
18
−
1
9
0
6
1
9
2
18

Plss help me out!!!!!!

Answers
Answer:
its D because they all match the sides
if 20 of the men are randomly selected, find the probability that their mean score is at least 513.2.
Answers
The probability that the mean score of 20 randomly selected men is at least 513.2 is approximately 0.217.
To find the probability that the mean score of 20 randomly selected men is at least 513.2, we need to use the central limit theorem.
Assuming that the scores of men are normally distributed with a mean of μ and a standard deviation of σ, the sample mean of a random sample of size n (in this case, n=20) will be normally distributed with a mean of μ and a standard deviation of σ/sqrt(n).
Let X be the score of a randomly selected man. We know that μ = 510 and σ = 20. Therefore, the sample mean of 20 randomly selected men will be normally distributed with a mean of 510 and a standard deviation of 20/sqrt(20) = 4.47.
To find the probability that the mean score of 20 randomly selected men is at least 513.2, we can standardize the distribution of the sample mean using the z-score formula:
z = (x - μ) / (σ / sqrt(n))
where x is the value we want to find the probability for, μ and σ are the mean and standard deviation of the population, and n is the sample size.
Substituting the given values, we get:
z = (513.2 - 510) / (4.47)
z ≈ 0.784
Using a standard normal distribution table or calculator, we can find the probability that a standard normal random variable is greater than or equal to 0.784:
P(Z ≥ 0.784) ≈ 0.217
Click the below link, to learn more about probability:
https://brainly.com/question/14210034
#SPJ11
when two sides and an angle are given at least one triangle can be formed. True or False
Answers
The answer is TRUE, When two sides and an angle are given at least one triangle can be formed.
When two sides and an angle are given, it is possible to form a unique triangle if the given angle is between the two given sides (i.e., the angle is not included by the two given sides). This is known as the Side-Angle-Side (SAS) criterion, which states that if two sides and the angle between them are given, then a unique triangle can be formed.
For example, if we are given that the length of side AB is 5 cm, the length of side AC is 7 cm, and the angle BAC is 60 degrees, then we can use this information to construct a unique triangle ABC.
However, if the given angle is not between the two given sides, then it is not possible to form a unique triangle. In this case, we would need to be given additional information, such as another angle or side length, to determine the dimensions and shape of the triangle.
In summary, the statement "When two sides and an angle are given at least one triangle can be formed" is true if the given angle is between the two given sides.
To know more about Triangle:
https://brainly.com/question/9738532
#SPJ11
Determine the number of integer solutions of x1 + x2 + x3 + x4 = 17, where
a. xi ≥ 0, 1 ≤ i ≤ 4
b. x1, x2 ≥ 3 and x3, x4 ≥ 1
c. xi ≥ -2, 1 ≤ i ≤ 4
d. x1 , x2 , x3 > 0 and 0 < x4 ≤ 10
Answers
a. The number of integer solutions to the equation x1 + x2 + x3 + x4 = 17, where xi ≥ 0 for 1 ≤ i ≤ 4, is 1140.
b. The number of integer solutions to the equation x1 + x2 + x3 + x4 = 17, where x1, x2 ≥ 3 and x3, x4 ≥ 1, is 364.
c. The number of integer solutions to the equation x1 + x2 + x3 + x4 = 17, where xi ≥ -2 for 1 ≤ i ≤ 4, is 23751.
d. The number of integer solutions to the equation x1 + x2 + x3 + x4 = 17, where x1, x2, x3 > 0 and 0 < x4 ≤ 10, is 560.
a. For the equation x1 + x2 + x3 + x4 = 17, where xi ≥ 0 for 1 ≤ i ≤ 4, we can use the stars and bars combinatorial technique. We have 17 stars (representing the value 17) and 3 bars (dividers between the variables). The stars can be arranged in (17 + 3) choose (3) ways, which is (20 choose 3).
Therefore, the number of integer solutions is (20 choose 3) = 1140.
b. For the equation x1 + x2 + x3 + x4 = 17, where x1, x2 ≥ 3 and x3, x4 ≥ 1, we can subtract the minimum values of x1 and x2 from both sides of the equation. Let y1 = x1 - 3 and y2 = x2 - 3. The equation becomes y1 + y2 + x3 + x4 = 11, where y1, y2 ≥ 0 and x3, x4 ≥ 1.
Using the same technique as in part a, the number of integer solutions for this equation is (11 + 3) choose (3) = (14 choose 3) = 364.
c. For the equation x1 + x2 + x3 + x4 = 17, where xi ≥ -2 for 1 ≤ i ≤ 4, we can shift the variables by adding 2 to each variable. Let y1 = x1 + 2, y2 = x2 + 2, y3 = x3 + 2, and y4 = x4 + 2. The equation becomes y1 + y2 + y3 + y4 = 25, where y1, y2, y3, y4 ≥ 0.
Using the same technique as in part a, the number of integer solutions for this equation is (25 + 4) choose (4) = (29 choose 4) = 23751.
d. For the equation x1 + x2 + x3 + x4 = 17, where x1, x2, x3 > 0 and 0 < x4 ≤ 10, we can subtract 1 from each variable to satisfy the conditions. Let y1 = x1 - 1, y2 = x2 - 1, y3 = x3 - 1, and y4 = x4 - 1. The equation becomes y1 + y2 + y3 + y4 = 13, where y1, y2, y3 ≥ 0 and 0 ≤ y4 ≤ 9.
Using the same technique as in part a, the number of integer solutions for this equation is (13 + 3) choose (3) = (16 choose 3) = 560.
Therefore:
a. The number of integer solutions is 1140.
b. The number of integer solutions is 364.
c. The number of integer solutions is 23751.
d. The number of integer solutions is 560.
To learn more about equations visit : https://brainly.com/question/29174899
#SPJ11
Once a model of reality is constructed around certain assumptions, it can be tested to determine its value in Group of answer choices predicting outcomes. producing data. graphing equations.
Answers
Once a model of reality is constructed around certain assumptions, it can be tested to determine its value in predicting outcomes.
Once a model of reality is constructed around certain assumptions, it can be tested to determine its value in predicting outcomes. This involves comparing the model's predictions with actual observed data or outcomes to assess its accuracy and reliability. By testing the model against real-world data, we can evaluate its validity and determine if it accurately represents the underlying reality or phenomenon being studied.
Producing data and graphing equations are related activities that can be part of the process of testing a model, but they are not the primary purpose of the model itself. Producing data involves collecting and generating empirical data that can be used to assess the model's predictions or outcomes. Graphing equations can be a way to visualize the relationships between variables in the model, but it is not the main purpose of the model itself. The primary purpose of constructing a model is to make predictions or generate hypotheses about how a system or phenomenon works, and testing these predictions against real-world outcomes is the key step in evaluating the model's value.
To know more about Real-world data refer here:
https://brainly.com/question/17544139
#SPJ11
Find the slope and the equation of the tangent line to the graph of the function at the given value of x. y=x 4
−10x 2
+9;x=1 The slope of the tangent line is (Simplify your answer.) The equation of the tangent line is
Answers
The equation of the tangent line represents a straight line that passes through the point of tangency and has a slope of -16.
The slope of the tangent line to the graph of the function y = x^4 - 10x^2 + 9 at x = 1 can be found by taking the derivative of the function and evaluating it at x = 1. The equation of the tangent line can then be determined using the point-slope form.
Taking the derivative of the function y = x^4 - 10x^2 + 9 with respect to x, we get:
dy/dx = 4x^3 - 20x
To find the slope of the tangent line at x = 1, we substitute x = 1 into the derivative:
dy/dx (at x = 1) = 4(1)^3 - 20(1) = 4 - 20 = -16
Therefore, the slope of the tangent line is -16.
To find the equation of the tangent line, we use the point-slope form: y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope.
Given that the point of tangency is (1, y(1)), we substitute x1 = 1 and y1 = y(1) into the equation:
y - y(1) = -16(x - 1)
Expanding the equation and simplifying, we have:
y - y(1) = -16x + 16
Rearranging the equation, we obtain the equation of the tangent line:
y = -16x + (y(1) + 16)
To find the slope of the tangent line, we first need to find the derivative of the given function. The derivative represents the rate of change of the function at any point on its graph. By evaluating the derivative at the specific value of x, we can determine the slope of the tangent line at that point.
In this case, the given function is y = x^4 - 10x^2 + 9. Taking its derivative with respect to x gives us dy/dx = 4x^3 - 20x. To find the slope of the tangent line at x = 1, we substitute x = 1 into the derivative equation, resulting in dy/dx = -16.
The slope of the tangent line is -16. This indicates that for every unit increase in x, the corresponding y-value decreases by 16 units.
To determine the equation of the tangent line, we use the point-slope form of a linear equation, which is y - y1 = m(x - x1). We know the point of tangency is (1, y(1)), where x1 = 1 and y(1) is the value of the function at x = 1.
Substituting these values into the point-slope form, we get y - y(1) = -16(x - 1). Expanding the equation and rearranging it yields the equation of the tangent line, y = -16x + (y(1) + 16).
The equation of the tangent line represents a straight line that passes through the point of tangency and has a slope of -16.
To learn more about tangent click here:
brainly.com/question/10053881
#SPJ11