Let X be a random variable with Poisson distribution of
parameter Lamda: Calculate
E (cos (\thetaX))
Answers
The expectation is 0.25.
Poisson distribution:Poisson distribution is a discrete distribution which is used to model events that occur in the specified interval of time. Parameter of Poisson distribution is \(\lambda\), which describes the average number of events occurring in the given interval of time.
The given information is:
E(X) = In 2
X ~ Poi( \(\lambda\) ) where \(\lambda\), = In 2
\(f(x)=\frac{e^-^\lambda\lambda^x}{x!}\)
It is known that cos(\(\pi x\))\(=(-1)^x\), for x = 1, 2, 3...
To calculate the value of the required expectation.
\(E(cos(\pi x))=\sum^\infty_x_=_0 (-1)^xf(x)\\\\E(cos(\pi x))=\sum^\infty_x_=_0(-1)^x\frac{e^-^\lambda(\lambda)^x}{x!}\\ \\E(cos(\pi x))=e^-^\lambda\sum^\infty_x_=_0\frac{(-\lambda)^x}{x!}\)
Expansion of exponential function is as follows
\(e^a=\sum^\infty_x_=_0\frac{(a)^x}{x!}\)
Therefore, further calculation can be done as
\(E(cos(\pi x))=e^-^\lambda \,e^-^\lambda\\\\E(cos(\pi x))=e^-^2^\lambda\\\\E(cos(\pi x))=e^-^2^(^I^n^ 2^)\\\\E(cos(\pi x))=e^(^I^n^ 2^)^2\\\\E(cos(\pi x))=\frac{1}{4}\)
Therefore, the expectation is 0.25.
Learn more about Poisson distribution at:
https://brainly.com/question/30388228
#SPJ4
The given question is incomplete, complete question is:
Let X be a Poisson random variable with E(X) =In 2. Calculate \(E[cos(\pi x)]\).
Related Questions
can someone help me asap

Answers
ASK ONE QUESTION!!
But to help you with one, the problem is.... h(x) + x with power of 2 - 5x
ANSWER= x(h+x−5)
SOLUTION= x(x+h−5) you had this equation and then you factor out x
Consider the function g(x)=−(x−1)^3−2. Which ordered pair lies on the inverse of the function?
(62,−3)
(−4, 123)
(3, 1)
(3,−6)
Answers
The ordered pair lie on the inverse of the function is (62,−3).
Option A is the correct answer.
What is a function?A function is a relationship between inputs where each input is related to exactly one output.
Example:
f(x) = 2x + 1
f(1) = 2 + 1 = 3
f(2) = 2 x 2 + 1 = 4 + 1 = 5
The outputs of the functions are 3 and 5
The inputs of the function are 1 and 2.
We have,
f(x) = -(x - 1)³ - 2
The inverse of f(x).
y = -(x - 1)³ - 2
interchange x and y and solve for y.
x = -(y - 1)3 - 2
(y - 1)³ = -2 - x
(y - 1)³ = -(2 + x)
Cuberoot on both sides.
y - 1 = ∛-(2 + x)
y = ∛-(2 + x) + 1
Now,
Substitute in the inverse of g(x).
(62, -3) = (x, y)
(−4, 123) = (x, y)
(3, 1) = (x, y)
(3,−6) = (x, y)
So,
y = ∛-(2 + x) + 1
y = ∛-(2 + 62) + 1
∛-1 = -1
y = -1∛64 + 1
y = -1 x 4 + 1
y = -4 + 1
y = -3
So,
(62, -3) ______(1)
And,
y = ∛-(2 + x) + 1
y = ∛-(2 - 4) + 1
∛-1 = -1
y = ∛(-2 + 4) + 1
y = ∛2 + 1
y = 1.26 + 1
y = 2.26
So,
(-4, 2.26) _______(2)
And,
y = ∛-(2 + x) + 1
y = ∛-(2 + 3) + 1
∛-1 = -1
y = -1∛5 + 1
y = -1 x 1.71 + 1
y = -1.71 + 1
y = -0.71
So,
(3, -0.71) _______(3)
And,
y = ∛-(2 + x) + 1
y = ∛-(2 + 3) + 1
∛-1 = -1
y = -1∛5 + 1
y = -1 x 1.71 + 1
y = -1.71 + 1
y = -0.71
So,
(3, -0.71) ______(4)
Thus,
From (1), (2), (3), (4) we see that,
(62, -3) is the solution to the inverse of g(x).
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ1
determine the distance travelled by the car during this time D =(2m x t2)/2
Answers
Answer:
D = 2mt
Step-by-step explanation:
D = (2m × 2t)/2
\( \sf \: d \: = \frac{2m \times t(2)}{2} \)
\( \rightarrow \: \sf \: d = \frac{2m \times 2t}{2} \)
\( \rightarrow \: \sf \: d = \frac{4mt}{2} \)
\( \rightarrow \: \sf \: d = 2mt\)
~Done~
------
anders makes scones using sugar,butter and flour in the ratio 1:2:8. He makes the scones using 100g of sugar, 300g of butter and 400g of flour.How much of each ingredient does he use?
Answers
Based on the ratio, Anders uses 72.73g of sugar, 145.46g of butter, and 581.84g of flour to make his scones.
Find the number by the ratioAnders makes scones using the ratio 1:2:8 for sugar, butter, and flour respectively. This means that for every 1 gram of sugar, he uses 2 grams of butter and 8 grams of flour.
To find out how much of each ingredient he uses, we can use the following steps:
1. Add the ratios together: 1 + 2 + 8 = 11
2. Divide the total amount of ingredients by the sum of the ratios: 100 + 300 + 400 = 800 / 11 = 72.73
3. Multiply each ratio by the result from step 2 to find the amount of each ingredient:
Sugar: 1 x 72.73 = 72.73g
Butter: 2 x 72.73 = 145.46g
Flour: 8 x 72.73 = 581.84g
Learn more about ratio at https://brainly.com/question/13419413
#SPJ11
Write an expression equivalent to -4(-6m - 7).
Answers
Answer: 24m+28
Step-by-step explanation:
Distribute the negative four among the two terms.
Answer:
\((12*2)m+(-56/-2)\)
I hope this helped :)
If both p and 2p+1 are prime, then 2p+1 is a safe prime and p is what other kind of prime, whose namesake—the first woman to win a prize from the Paris Academy of Sciences, for work on elasticity—used them to investigate Fermat's Last Theorem?
Answers
If both p and 2p+1 are prime, then 2p+1 is a safe prime and p is a Sophie Germain prime.
Sophie Germain was a French mathematician who used these primes to investigate Fermat's Last Theorem, a famous mathematical conjecture that was finally proved in 1994 by Andrew Wiles. A safe prime is a prime number of the form 2p+1, where p is also a prime number, and it is called "safe" because it has some cryptographic properties that make it useful in certain encryption schemes. In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers a, b, and c satisfy the equation an + bn = cn for any integer value of n greater than 2. The cases n = 1 and n = 2 have been known since antiquity to have infinitely many solutions.
Learn more about safe prime here, https://brainly.com/question/145452
#SPJ11
What is the equation of a line that is parallel to the line 2x + 5y = 10 and passes through the point (-5, 1)? Check all
that apply.
O
y
O 2x + 5y = -5
y=-2x-3
O 2x + 5y = -15
O y - 1= -2(x + 5)
Answers
The required equation of the line is 2x + 5y + 5 = 0
What is an equation?
Equations are used to describe geometric shapes in Cartesian geometry. Because the equations under consideration, such as implicit equations or parametric equations, contain an unlimited number of solutions, the goal has shifted: instead of directly stating the solutions or counting them, which is impossible, one utilizes equations to investigate the features of figures. This is the fundamental concept of algebraic geometry, a significant branch of mathematics. Algebra is concerned with two types of equations: polynomial equations and the particular case of linear equations. Polynomial equations have the form P(x) = 0, where P is a polynomial, while linear equations have the form ax + b = 0, where a and b are parameters, when there is only one variable. Algorithms are used to solve equations from either family.
Given equation of the line is 2x + 5y = 10
or, 5y = -2x + 10
or, y = -2x/5 + 2
slope of the equation, m = -2/5
Since the lines are parallel, so the required equation of the line is
y-1 = (-2/5)(x+5)
or, 5(y-1) = -2(x+5)
or, 5y-5 = -2x-10
or, 2x + 5y + 5 = 0
Hence, the required equation of the line is 2x + 5y + 5 = 0
i.e. 2x + 5y = -5
To know more about an equation, click on the link
https://brainly.com/question/27893282
#SPJ13
Six times the sum of half a number x and 12 is 30
Answers
Answer:
-14
Step-by-step explanation:
Translate the words to an equation
6(\(\frac{x}{2}\) + 12) = 30
Divide both sides by 6
\(\frac{x}{2}\) + 12 = 5
Multiply both sides by 2
x + 24 = 10
Subtract 24 from both sides
x = -14
Graph the solution set of the system. Please my graph to point.-2x-y ≥2 y ≥-2 x ≥-4

Answers
To graph the solution set of the system, first, we have to graph each inequality.
First, express each inequality as an equation.
\(\begin{gathered} -2x-y=2 \\ y=-2 \\ x=-4 \end{gathered}\)Then, graph each equation, they represent lines. The second and third equations are horizontal and vertical lines, respectively. While the first equation has an inclination, to graph the first one, we have to find the zeros of the equation.
Y - INTERCEPT (x = 0).
\(-2(0)-y=2\to y=-2\)The y-intercept is (0,-2).
X - INTERCEPT (y = 0).
\(-2x-0=2\to-2x=2\to x=\frac{2}{-2}\to x=-1\)The x-intercept is (-1,0).
Using the intercept points, we can draw the line. Also, let's draw the other two.
Once we have all the lines, evaluate the inequalities to see which area is the solution.
y ≥-2 indicates that all the real numbers above or equal to -2 must be the solution.
x ≥-4 indicates that all the real numbers on the right of the line must be the solution.
Now, evaluate the first inequality with a test point (0,0).
\(-2x-y\ge2\to-2(0)-0\ge2\to0\ge2\)But, we know that zero is not greater than 2, which means the solutions must be below the red line because it can't include the point (0,0).
Unite all three areas to get the final solution set.
Therefore, the purple triangle represents the solution set.

Matt wanted to buy a new mountain bike. The bike he wants to buy costs $319. He received $85 for his birthday and earned another $147 from his job as an Uber driver. How much more money will he need in order to buy the mountain bike?
Answers
Answer:
he will need $87 more to buy a mountain bike.
Step-by-step explanation:
85+147= 232 dollars that he has all together.
subtract that from the total cost of the bike (319-233= $87 more to buy a bike.)
I need to show all my work, please.
2r + 49 = -8 (-r - 5)
Answers
Answer:
2r+49=-8(-r-5)
-8*-1r -8*-5
2r+49=8r+40
40-49
2r=8r-9
2r-8r
-6r=-9
/-6
r=3/2
Let A = 2x + 5 and B = x2 - 4x – 1
Find A - B
PLEASE HELP
Answers
First, combine your like terms, 2x, 2x, and -4x, which equals to 0x or x. Then, you add the regular numbers together, +5 and -1, which equals to 4. Now that we have our numbers, our full answer will be x-4.
Look at the equation.
X-3 = 12
Which value of x makes this equation true?
4
(b9
с
15
d) 36
Answers
Answer:
c) 15
Step-by-step explanation:
Plugging in the value of x as 15 in the equation,
15-3 which is equal to 12
4.
Alexander was able to travel 25% of 150 km journey in the morning. How many
journey is still left to be traveled?
Answers
Answer: 112.5 km5.
-
Alexander was able to cover 25% of 150 km journey in the morning. What percent of journey is still left to be covered?
112.5km5
Question 2 of 6 View Policies Current Attempt in Progress Express the following as a linear combination of u =(3, 1,6), v = (1.-1.4) and w=(8,3,8). (14, 9, 14) = ____ u- _____ v+ _____
Answers
Answer: The given vector can be expressed as a linear combination of u, v, and w as (14, 9, 14) = u - v + 3w.
Question: Express the following as a linear combination of u =(3, 1,6), v = (1.-1.4) and w=(8,3,8). (14, 9, 14) = ____ u- _____ v+ _____
Current Progress: To express the given vector as a linear combination of u, v, and w, we need to find scalars a, b, and c such that (14, 9, 14) = a*u + b*v + c*w.
Step 1: Write the equation in component form:
(14, 9, 14) = (3a + b + 8c, a - b + 3c, 6a + 4b + 8c)
Step 2: Equate the corresponding components and solve for a, b, and c:
3a + b + 8c = 14
a - b + 3c = 9
6a + 4b + 8c = 14
Step 3: Solve the system of equations using any method (substitution, elimination, etc.). One possible solution is a = 1, b = -1, and c = 3.
Step 4: Plug the values of a, b, and c back into the linear combination equation:
(14, 9, 14) = 1*u + (-1)*v + 3*w
Step 5: Simplify the equation:
(14, 9, 14) = u - v + 3w
Answer: The given vector can be expressed as a linear combination of u, v, and w as (14, 9, 14) = u - v + 3w.
Learn more about Express
brainly.com/question/28172855
#SPJ11
Consider functions f and g.
f(X) = X2 + 24x + 144
g(x) = X3 – 216
-
Which expression is equal to f(x) + g(x)?
Answers
Option A is correct. The expression f(x)+g(x) is equal to \(x^3+x-204\).
The given two functions are f(x) and g(x):
\(f(x)=\sqrt{x^2+24x+144}\)
\(g(x)=x^3-216\)
We need to find f(x)+g(x).
Let us simplify f(x) function:
\(f(x)=\sqrt{x^2+24x+144}\)
\((x+12)^2=x^2+24x+144\) by using \((a+b)^2\) formula.
\(f(x)+g(x)=\sqrt{x^2+24x+144}+x^3-216\)
\(=\sqrt{(x+12)^2}+x^3-216\)
The square root gets cancelled.
\(=x+12+x^3-216\)
Combine like terms:
\(=x^3+x-204\)
Hence, the expression f(x)+g(x) is equal to \(x^3+x-204\). Option A is correct.
To learn more on Functions click:
https://brainly.com/question/30721594
#SPJ12
Complete question:
Consider functions f and g.
f(X) =√(X^2 + 24x + 144)
g(x) = X^3 – 216
Which expression is equal to f(x) + g(x)?
(a) x^3+x-204
(b) x^3+x^2+24x-72
(c)x^4-204
(d) x^3+x-228
Helppp!!!!!!!!!!!!!!!!!!!!!

Answers
The value of x is equal to 15°
How to determine the value of x?In Mathematics and Geometry, the sum of the exterior angles of both a regular and irregular polygon is always equal to 360 degrees.
Note: The given geometric figure (regular polygon) represents a pentagon and it has 5 sides.
By substituting the given parameters, we have the following:
3x + 4x + 8 + 5x + 5 + 6x - 1 + 5x + 3 = 360°.
3x + 4x + 5x + 6x + 5x + 8 + 5 - 1 + 3 = 360°.
23x + 15 = 360°.
23x = 360 - 15
23x = 345
x = 345/23
x = 15°.
Read more on sum of interior angles here: brainly.com/question/13293407
#SPJ1
a rectangular poster is to contain 392 square inches of print. the margins at the top and bottom of the poster are to be 2 inches, and the margins on the left and right are to be 1 inch. what should the dimensions of the poster be (in inches) so that the least amount of poster is used? (enter your answers as a comma-separated list.)
Answers
The dimensions of the poster with an area of 392 square inches is equal to 14 inches and 28 inches.
Area of rectangular poster to print = 392 square inches
Let us assume that dimensions of the posters are,
Width of the poster is x inches and the length of the poster is y inches.
Area of the rectangular poster is,
xy = 392
Add 2 inches to the top and bottom margins for a total of 4 inches
And 1 inch to the left and right margins for a total of 2 inches.
Total area of the poster including the margins using the following equation,
Total area = (x + 2) × (y + 4)
Minimize the total area of the poster while still satisfying the area constraint.
Use the first equation to solve for one variable
And substitute it into the second equation,
y = 392/x
Total area = (x + 2) × (392/x + 4)
⇒ Total area = 4x + 392 +784/x + 8
⇒Total area = 4x + 400 +784/x
Minimize the total area, take the derivative of this expression with respect to x and set it equal to 0,
d/dx (4x + 400 +784/x ) = 0
⇒ 4 + 0 - 784/x² = 0
⇒ x² = 784 /4
⇒ x = 14
Substituting this value of x back into the equation for y, we get,
y = 392/14
= 28
Therefore, the dimensions of the poster should be 14 inches by 28 inches.
Learn more about dimensions here
brainly.com/question/29803134
#SPJ4
Let x and y be real numbers such that x < 2y. Prove that if
7xy ⤠3x2 + 2y2, then 3x ⤠y.
Answers
To prove that 3x ≤ y, assume the opposite, that is, 3x > y, rearrange the inequality substitute x < 2y and simplify, contradict the given condition that x < 2y, therefore, concluding that 3x ≤ y.
Start by assuming the opposite, that is, 3x > y.
From the given inequality,\(7xy \leq 3x^2 + 2y^2,\), we can rearrange to get:
\(7xy - 3x^2 \leq 2y^2\)
We can substitute \(x < 2y\) into this inequality:
\(7(2y)x - 3(2y)^2 \leq 2y^2\)
Simplifying, we get:
\(y(14x - 12y) \leq 0\)
Since y is a real number, this means that either y ≤ 0 or 14x - 12y ≤ 0.
If y ≤ 0, then 3x ≤ y is trivially true.
If 14x - 12y ≤ 0, then we can rearrange to get:
3x ≤ (12/14)y
3x ≤ (6/7)y
3x < y (since we assumed 3x > y)
But this contradicts the given condition that x < 2y, so our assumption that 3x > y must be false.
Therefore, we can conclude that 3x ≤ y.
Know more about inequality here:
https://brainly.com/question/25275758
#SPJ11
A ball is dropped from a ladder. After the first bounce, the ball is 13. 5 feet off the ground. After the second bounce, the ball is 10. 8 feet, off the ground. After the third bounce, the ball is 8. 64 feet off the ground.
a. ) Write an equation to represent how high the ball is after each bounce:
b. ) How high is the ball after 5 bounces?
Answers
The height of the ball after five bounces is 2.28 feet. The problem can be solved by writing an equation to determine the height of the ball after each bounce, where h is the initial height of the ladder and b is the number of bounces the ball has taken.
a) Write an equation to represent how high the ball is after each bounce:
The problem can be solved by writing an equation to determine the height of the ball after each bounce, where h is the initial height of the ladder and b is the number of bounces the ball has taken. Using this information, the equation is:
\(h = (3/4)^b * h\)
\(h = 13.5(3/4)^1\\\)
\(h = 10.8(3/4)^2\)
\(h = 8.64(3/4)^3\)
b) How high is the ball after 5 bounces?
The height of the ball after 5 bounces can be found by simply substituting b = 5 into the equation. The height of the ball is:
h = \((3/4)^5 * h\) = \((0.16875) * h\) = \((0.16875) * 13.5h\) = 2.28 feet
Therefore, the height of the ball after 5 bounces is 2.28 feet. To find out how high a ball is after each bounce and after five bounces, we can use the equation:
\(h = (3/4)^b * h\)
Where h is the height of the ladder and b is the number of bounces the ball has taken. For example, after the first bounce, the ball is 13.5 feet off the ground. So, if we use b = 1 in the equation, we get: \(h = (3/4)^1 * 13.5\)
h = 10.125 feet
Similarly, we can use the equation to find out the height of the ball after the second and third bounces, which are 10.8 and 8.64 feet respectively. After the fifth bounce, we need to substitute b = 5 in the equation. This gives us:
h\(= (3/4)^5 * h\)
h = 2.28 feet
Therefore, the height of the ball after five bounces is 2.28 feet.
To know more about height visit: https://brainly.com/question/29131380
#SPJ11
Calculate the area of the following figure:
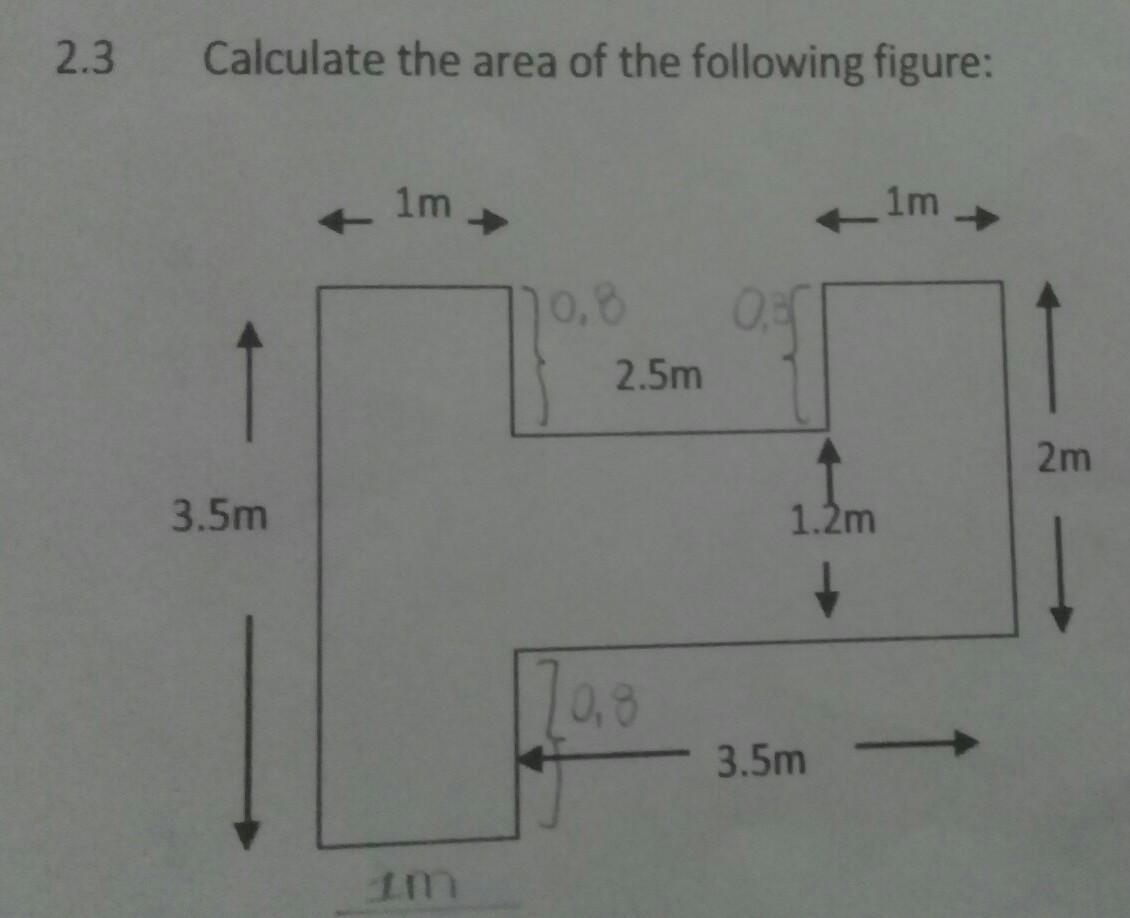
Answers
Step by step.
I like to break down figures like these into smaller figures as shown in the attachment.
We know that area (A) = Length x Width.
Figure 1 : 3.5 x 1 = 3.5m
Figure 2 : 2.5 x 1.2 = 3m
Figure 3 : 1 x 2 = 2m
Add the 3 figures together you get 8.5m

Answer:
Area => 8.5m2
Step-by-step explanation:
Hope this helps! (=`ω´=) x

Draw the net of the solid that best models the hay bales. Please include the correct dimensions on your net.

Answers
pls help due in an hour if you get it right ill mark you brainiest

Answers
Step-by-step explanation:
B to B'
( 7,-2) to (-2,-7)
(x,y) changed to (y,-x) this is a 90 degree clockwise rotation
Answer:
Step-by-step explanation:
It is a 90 degree clockwise rotation.
A = (2, -5)
A' = (-5, -2)
90° clockwise will reverse the x an y points and change the sign of x.
(x, y) becomes (y, -x)
You only need to use one point to figure the rotation.
Any help would be appreciated!
7/9+ 8/9 as a mixed number
Answers
Answer:
15/9 :))
is your answerrr
Answer:
15/9
Step-by-step explanation:
For this all you have to do is add the numerators.
So 7 + 8 = 15
The number is 15/9
Hope this helps ya!!
Ethan is watering his plants. He starts with a watering can filled with 32 ounces of water, and he pours 3.5 ounces onto each plant. When Ethan finishes watering his plants, he has 14.5 ounces of water left. How many plants does he have? Write and solve an equation to find the answer.
Answers
The number of plants Ethan has are 5.
What is Equation?Two or more expressions with an Equal sign is called as Equation.
Let x be the number of plants Ethan has.
Ethan uses 3.5 ounces of water for each plant, so he will use a total of 3.5p ounces of water.
If he starts with 32 ounces of water and ends up with 14.5 ounces
Total of 32 - 14.5 = 17.5 ounces of water.
As given the amount of water used is equal to the amount of water per plant times the number of plants:
3.5x = 17.5
Divide both sides by 3.5
x=5
Hence, , Ethan has 5 plants.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ9
g(n)= -2n-4
f(n)= 2n+1
find (g-f) (2)
Answers
step by step:
g(2)= -2(2)-4
-4-4=-8
f(2)= 2(2)+1
4+1=5
-8-5=-13
There are 19 animals in the field. Some are cows and some are ducks. There are 60 legs in all. How many of each animal are in the field?
Answers
Answer:
There are 11 cows and 8 ducks
Step-by-step explanation:
x will represent number of cows and (19-x) will represent ducks
\(4x+2(19-x)=60\)
multiply 2 with (19-x)
\(4x+38-2x=60\)
add your x's
\(2x+38=60\)
subtract 38 on both sides
\(2x=22\)
then divided 2 on both sides
\(x=11\) cows
now to find ducks subtract
\(19-11\)
your answer will be 8
So there are 11 cows and 8 ducks
to double check do this
\(11*4 + 8*16\\=44+16\\=60\)
me need a lot of help

Answers
I hope you have a good day!
NEEED HELPPP !!!!!!!!!!

Answers
Answer:
X + 7 + 2x + 19 = 35
Add like terms
3x + 26 = 35
-26 -26
3x = 9
/3 /3
X = 3
Sam is playing a game where he flips a coin and rolls a number cube labeled 1 through 6. He listed the possible outcomes in the sample space shown:
{(H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5)}
Which two elements did he leave out by mistake?
Answers
The correct elements he left out by mistake are (B) (H, 6) and (T, 4).
What is the sample space for a random experiment?Sample space is the set of all possible outcomes the considered random experiment can result to. Thus, suppose we toss a coin, then tossing a coin is a random experiment, and the sample space is {'head', 'tail'}.
We are Given that Sam is playing a game where he flips a coin and rolls a number cube labeled 1 through 6.
He listed the possible outcomes in the sample space as :
S' = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (T, 1), (T, 2), (T, 3), (T, 5), (T, 6)}.
We need to find the two elements that he left out while writing the sample space.
The complete sample space is;
S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
All the elements of S are in S' except the two (H, 6) and (T, 4).
Hence Sam left out the elements (H, 6) and (T, 4).
Learn more about the sample space of a random experiment here:
https://brainly.com/question/9773761
#SPJ1