Answers
Answer:
35997
Step-by-step explanation:
Related Questions
Can you please help me

Answers
Answer:
Fourth choice, 19/30
Step-by-step explanation:
Add 38 and 22 together, it's 60
Out of 60 times, he flipped heads 38 times, so it's 38/60
Simplify 38/60 with 2, 19/30
Please Help.......................

Answers
Answer:
I think its d
Step-by-step explanation:
bc it's the only one who has the = sign on both ends I'm not really sure tho I might of learned it a different way hope this helps
Answer:
8x - 2y = -14
16x - 6y = -18
Step-by-step explanation:
I haven't done this in a long time, but I believe my answer is correct.
Hope this helps!
Write this sets in set-builder notation. 17. {2,4,8,16,32,64...}
Answers
The set {2, 4, 8, 16, 32, 64...} can be represented in set-builder notation as {2ⁿ| n is a non-negative integer}.The given set consists of powers of 2, starting from 2 and increasing by doubling each time.
We can observe that each element in the set can be expressed as 2 raised to the power of some non-negative integer. To represent this set in set-builder notation, we use the form {x | condition on x}, where x represents the elements of the set and the condition specifies the pattern or property that the elements must satisfy. In this case, the condition is that the element must be a power of 2, which can be written as 2ⁿ, where n is a non-negative integer. Therefore, the set can be expressed as {2ⁿ| n is a non-negative integer}, indicating that the elements of the set are 2 raised to the power of all non-negative integers.
Learn more about integer here: https://brainly.com/question/199119
#SPJ11
Todd's living room is rectangular and measures 9 meters by 3 meters. Beginning in one corner, Todd walks the length of his living room and then turns and walks the width. Finally, Todd walks back to the corner he started in. How far has he walked? If necessary, round to the nearest tenth.
Answers
write the function in terms of unit step functions. find the laplace transform of the given function. f(t) = 5, 0 ≤ t < 4 −5, t ≥ 4
Answers
The Laplace transform of the given function f(t) is (5 - 5e^(-4s))/s.
We can write the given function f(t) in terms of unit step functions as follows:
f(t) = 5u(t) - 5u(t-4)
This expression gives us the value of f(t) as 5 for 0 ≤ t < 4, and as -5 for t ≥ 4.
To find the Laplace transform of f(t), we use the linearity property of Laplace transforms and the fact that the Laplace transform of a unit step function u(t-a) is given by e^(-as)/s. Therefore, we have:
L{f(t)} = L{5u(t)} - L{5u(t-4)}
= 5L{u(t)} - 5L{u(t-4)}
= 5 * [1/s] - 5 * [e^(-4s)/s]
Simplifying this expression, we get:
L{f(t)} = (5 - 5e^(-4s))/s
Therefore, the Laplace transform of the given function f(t) is (5 - 5e^(-4s))/s.
Learn more about Laplace transform here:
https://brainly.com/question/30759963
#SPJ11
is the complex vector space of polynomials consist of complex-valued functions of a complex variable?
Answers
The complex vector space of polynomials is a vector space over complex number fields and is composed of complex-valued functions of a complex variable.
A vector represents a mathematical entity with both magnitude and direction. When the vector elements are generally complex numerals, then the column space is referred to as complex. The set of polynomials in such a vector space generates the space over the domain of complex numbers by combining extra polynomials that are each specified portion and by multiplying each coefficient by the scalar.
In this vector space, the polynomials are vectors whereas the complex numerals are scalars. These requirements for the space are in addition also catered by this space, like the associativity and commutativity of vector addition, the presence of additive inverses, the distributivity of scalar multiplication over vector addition, and the existence of a neutral element with respect to vector addition.
Read more about complex vector space on:
https://brainly.com/question/14466269
#SPJ4
Two cyclists start from 98 miles apart and begin racing toward each other. Three hours later, they have not yet met and the distance between them is 2 miles. How fast is each of them biking if one bikes 3 mph slower than the other?
Answers
Answer:
18 and 21
Step-by-step explanation:
there are more than 7 shades of skin color. can you offer an explanation?
Answers
First and foremost, it is important to note that human skin color is determined by a variety of factors, including genetics, environmental influences, and geographic location. In fact, skin color is the result of the amount and type of melanin pigment produced by specialized cells in the skin called melanocytes.
There are two main types of melanin pigment: eumelanin and pheomelanin. Eumelanin is responsible for producing darker skin colors, while pheomelanin produces lighter skin colors. However, the amount and distribution of these pigments can vary greatly between individuals, resulting in a wide range of skin tones.
Additionally, skin color can also be influenced by factors such as sun exposure, age, and hormonal changes. For example, prolonged sun exposure can lead to darker skin, while aging and hormonal changes can cause changes in skin pigmentation. Furthermore, it is important to note that skin color is not always clearly defined or easily categorized into specific shades. There can be a great deal of variation within a single skin tone, as well as overlap between different skin tones. This is due to the complex interplay of genetic and environmental factors that contribute to skin color.
To know more about genetics visit:-
https://brainly.com/question/30459739
#SPJ11
A right triangle has an angle measure of 52.4 degrees. What is the value of 'x', the missing angle?
Answers
Answer:
The answer is 37.6 degrees
Step-by-step explanation:
Since a right angle is 90 degrees in total, to find the missing degree subtract 52.4 from 90 to find the value of x.
90-52.4= 37.6 degrees
37.6 degrees is your answer
Hope this helps
finally, what is the total distance the particle travels between time 0 0 and time 16 16 ?
Answers
Without knowing the specific form of the velocity function v(t), it is not possible to determine the exact distance traveled.
Why would we say so?The total distance traveled by a particle can be found by integrating its velocity over time. If the velocity of the particle at time t is given by the function v(t), then the total distance traveled between time t1 and t2 is given by:
distance = ∫v(t)dt from t1 to t2
In this case, we want to find the distance traveled between time 0 and time 16, so t1 = 0 and t2 = 16. Without knowing the specific form of the velocity function v(t), it is not possible to determine the exact distance traveled.
What is velocity?Velocity is a vector quantity that describes the rate at which an object changes its position in space. It is a combination of both speed and direction and is typically represented by the symbol v.
In physics, velocity is defined as the derivative of position with respect to time. If the position of an object at time t is given by the function x(t), then its velocity at time t is given by:
v(t) = dx(t)/dt
This means that velocity is the rate of change of position with respect to time. For example, if an object moves in a straight line from position x1 to x2 in time t, its average velocity during that time is given by:
v = (x2 - x1)/t
Velocity is an important concept in mechanics, as it is used to describe the motion of objects and to calculate various physical quantities, such as force and acceleration.
Learn more about quadratic equations here
https://brainly.com/question/14083225
#SPJ1
Victor wanted to know the height of a tree at his friend’s house. On Saturday morning, he measured the shadow of the tree along the ground to be 24 feet long. At the same time, he measured his own shadow to be 3 feet long. Victor is 6 feet tall. Find the height of the tree
Answers
Ratio remains same
Let that be x\(\\ \rm\rightarrowtail \dfrac{6}{3}=\dfrac{x}{24}\)
\(\\ \rm\rightarrowtail 2=x/24\)
\(\\ \rm\rightarrowtail x=48\)
Help my little sister shes pass due


Answers
3. 3x = 12
An open statement in math means that it utilizes variables, and can only be concluded as being "true" or "false". The problem would result in asking whether or not it is always true or not. In this case, x will be true when you plug in 4, however, it will not be true when you plug in any other number. Therefore, it is a closed statement that can be falsified.
4. Open.
The statement can be true if the variable g is 35, however, it is false if it is not. An open statement concludes that it may or may not be correct, thereby being open.
~
If u/8 -4 = 7, what does u equal
Answers
Answer:
88
Step-by-step explanation:
\(\frac{u}{8}-4=7 \\ \\ \frac{u}{8}=11 \\ \\ u=88\)
Answer:u=88
Step-by-step explanation:
Builtrite has calculated the average cash flow to be $14,000 with a standard deviation of $5000. What is the probability of a cash flow being between than $16,000 and $19,000 ? (Assume a normal distribution.) 16.25% 18.13% 23.90% 2120%
Answers
The correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
The probability of a cash flow between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
Drink Price Primary School Secondary School Juice £1.50 21 45 Water £0.80 12 115 Coca-Cola £1.20 33 51 Sprite £1.20 45 45 Milk £1.40 9 12 Chocolate Milk £1.90 30 32 What was the daily turnover for the drink vender in the Secondary School? O A. £353.20 O B. £247.05 O C. £452.90 D. £345.50
Answers
The daily turnover for the drink vendor in the secondary school is £352.30, which is closest to option A, £353.20 i.e. Option A is the correct answer
To calculate the daily turnover for the drink vendor in the secondary school, we need to consider the number of drinks sold and the price of each drink. From the given table, we can see that for secondary school, the number of Juice drinks sold is 45, the number of Water drinks sold is 115, the number of Coca-Cola drinks sold is 51, the number of Sprite drinks sold is 45, the number of Milk drinks sold is 12, and the number of Chocolate Milk drinks sold is 32.
Using these numbers, we can calculate the daily turnover for each drink by multiplying the number of drinks sold by the price of each drink. For example, for Juice, the price is given as £1.50 and the number of drinks sold is 45, so the total turnover for Juice is £1.50 x 45 = £67.50. Similarly, we can calculate the daily turnover for each drink sold in the secondary school.
Finally, we add up all the daily turnovers for each drink sold in the secondary school to get the total daily turnover for the drink vendor in the secondary school. The calculated total turnover is £352.30, which is closest to the option A, £353.20.
For the secondary school, the turnover can be calculated as follows:
Juice: £1.50 x 45 = £67.50
Water: £0.80 x 115 = £92.00
Coca-Cola: £1.20 x 51 = £61.20
Sprite: £1.20 x 45 = £54.00
Milk: £1.40 x 12 = £16.80
Chocolate Milk: £1.90 x 32 = £60.80
Total turnover = £352.30
practice more on turnover here: brainly.com/question/29214829
#SPJ11
The slope at [1,pi/2] from -8x^3/siny
Answers
As a result, the function's slope at [1, pi/2] is [-24] as where the derivative of y with respect to x is denoted by y'.
what is slope ?The slope of a line in mathematics serves as a gauge for how steep it is. Between any two locations on the line, it is the proportion of the shift in the vertical motion (y) to the shift in the horizontal position (x). If we take into account two points on a line, (x1, y1) and (x2, y2), we can use the following formula to get the slope of the line: slope equals (y2 - y1)/. (x2 - x1) . Depending on the line's direction, the inclination can be zero, positive, or negative. A line with a positive slope is moving upward from left to right, whereas one with a negative slope is moving downward.
given
Finding the derivative of the given function with respect to x can be our first step. By applying the quotient rule, we get:
F(x) = 8x 3 sin (y)
\([(sin(y))(-24x2)] = f'(x) - (-8x^3) (cos(y))(y')] / (sin(y))^2\)
where the derivative of y with respect to x is denoted by y'.
We can change x=1 and y=pi/2 in the equation above since we are interested in the slope at the position [1, pi/2].
Due to the fact that cos(pi/2) = 0 and sin(pi/2) = 1, we can write:
\(f'(1) = [(1)(-24) (-24) - (-8)(1)(0)(y')] / (1)^2\)
f'(1) = -24 + 0
f'(1) = -24
As a result, the function's slope at [1, pi/2] is [-24] as where the derivative of y with respect to x is denoted by y'.
To know more about slope visit:
https://brainly.com/question/3605446
#SPJ1
What does this equal? Show your work pls
Answers
Answer:
can u show us the question
Step-by-step explanation:
Find the root of the equations using the Newton Raphson method. y=f(x)=e^x−x x0=0 ,e^x−3x=3 root of the equation (0,1) in the range x^3+2x^2+6x+3=0 root of the equation (−1,0) in the range
Answers
The root of this equation is determined to be approximately 0.567143.The root is found to be approximately -0.673253.
The Newton-Raphson method is an iterative numerical technique used to find the roots of equations. In the first equation, y = f(x) = e^x - x, the initial approximation x0 is set to 0. By applying the Newton-Raphson method, successive approximations of the root are calculated until convergence is achieved. The root of this equation is determined to be approximately 0.567143.
In the second equation, x^3 + 2x^2 + 6x + 3 = 0, the root is sought within the range (-1, 0). The Newton-Raphson method is employed again, starting with an initial approximation x0 of -1. Through iterative calculations, the root is found to be approximately -0.673253.
Both equations demonstrate the effectiveness of the Newton-Raphson method in finding roots within specific ranges by iteratively refining approximations until a satisfactory solution is obtained.
For more information on effectiveness visit: brainly.com/question/33225255
#SPJ11
Write the slope-intercept form of the equation of a line with a slope of -5/8 that passes through the point (-14,6)

Answers
Answer:
y = -5/8x - 11/4
Step-by-step explanation:
Since we already know the slope which is -5/8. This will be the m in the equation.
To find the y-intercept, plug the coordinates into the equation, which is
y= -5/8 + b
6 = -5/8(-14) + b
6 = 35/4 + b
= -11/4 = b
Which ordered pair is a solution to
the equation
3x + 9y = 27 ?
Answers
Answer:
x=9-3y
Step-by-step explanation:
- Move the variable to the right & change its sign
3x + 9y = 27
- Divide both sides by 3
3x = 27 - 9y
- Write the solution x in parametric form
x=9-3y
- Solution:
x= 9-3y
You have been saving nickels, dimes, and quarters in a jar for about a year. You decide to see how much money you've saved up. When you get everything counted it turns out you have 361 total nickels, dimes, and quarters worth a total of $41.45. You think is is odd that you have exactly twice as many dimes as quarters. Find the number of each coin.
Answers
Answer:
No. of Nickels = 127
No. of Dimes = 156
No. of Quarters = 78
Step-by-step explanation:
First we need to form a system of equations representing the situation. So, first we let:
x = number of nickel coins
y = number of dimes
z = number of quarters
Now, we know that the total coins are 361. Therefore,
x + y + z = 361 ----------- equation (1)
It is also given that there are twice as many dimes as quarters:
y = 2z
y - 2z = 0 ----------------equation (2)
Now, we have a total worth of $41.45. A dime is worth $0.1, nickel is worth $0.05 and a quarter is worth $0.25. Therefore,
0.05x + 0.1y + 0.25z = 41.45 ----------------- equation (3)
Simultaneously solving the three equations, we get:
x = 127, y = 156, z = 78
Hence,
No. of Nickels = 127
No. of Dimes = 156
No. of Quarters = 78
pregnancy length (in days) is a normally distributed random variable with a mean of 266 days and a standard deviation of 16 days. births that occur before 245 days are considered premature. what is the probability that a randomly selected newborn baby is premature? use the appropriate applet. enter a number in decimal form, e.g. 0.68 not 68 or 68%.
Answers
The probability of a birth occurring before 245 days, which is the probability of a newborn baby being premature.
To do this, we need to calculate the area under the normal distribution curve that represents the probability of a birth occurring before 245 days.
We can use a standard normal distribution table or an appropriate applet to find this probability. Using the applet, we can enter the mean, standard deviation, and the value of 245 days to find the probability.
In mathematical terms, we can write this as:
P(birth before 245 days) = probability of a randomly selected newborn baby being premature
= P(X < 245), where X is the random variable representing pregnancy length
Using the normal distribution table or applet, we can find P(X < 245) by calculating the area under the normal distribution curve to the left of 245 days.
To know more about probability here
https://brainly.com/question/11234923
#SPJ4
Need help asap!
1. sin theta =
-15/17
8/17
15/17
-8/17
2. cos theta =
-8/17
15/17
-15/17
8/17
3. tan theta =
8/15
15/8
-15/17
-15/8
4. csc theta =
-17/8
-17/15
17/15
17/8
5. sec theta =
17/15
-17/8
-17/15
17/8
6. cot theta =
15/8
-15/17
-15/8
8/15
Answers
sin theta = opposite/hypotenuse = -15/17
cos theta = adjacent/hypotenuse = 8/17
tan theta = opposite/adjacent = -15/8
Then, using the reciprocal identities, we can determine csc theta, sec theta, and cot theta as:
csc theta = 1/sin theta = -17/15
sec theta = 1/cos theta = 17/8
cot theta = 1/tan theta = -8/15
Therefore, the answers are:
1. sin theta = -15/17
2. cos theta = 8/17
3. tan theta = -15/8
4. csc theta = -17/15
5. sec theta = 17/8
6. cot theta = -8/15
Compare the following sets of data for June 2006 and June 2005.
Canadian Housing Prices by City ($)
June 2006
June 2005
Canadian City
Vancouver
Victoria
Calgary
Edmonton
Regina
Saskatoon
Ottawa
Toronto
Montreal
Fredericton
Saint John
Halifax
Sources: MLS and Remax
Mean:
1. Find the measures of central tendency for each. State any conclusions found.
Median:
Mode:
508 435
538 913
367 033
254 240
137 022
160 548
260 458
358 035
222 879
136 371
127 586
201 316
Conclusions:
June 2006
June 2006
422 843
469 588
245 803
199 409
132 054
139 728
254 725
345 065
210 740
134 334
125 455
184 853
June 2006
June 2005
June 2005
June 2005

Answers
The Mean for June 2006 and 2005 is $345,909 and $335,977 respectively. The median for June 2006 and 2005 is $254,000 and $139,000 respectively, there's no mode in this question.
Explain mean, median, mode briefly?In statistics, the mean, mode, and median are three measures of central tendency that describe a set of numerical data.
The mean is the average of a set of numbers, calculated by adding up all the values and dividing by the number of values. For example, if a set of data contains the values {1, 2, 3, 4, 5}, the mean is (1 + 2 + 3 + 4 + 5) / 5 = 3.
The mode is the value that appears most frequently in a set of data. For example, if a set of data contains the values {1, 2, 2, 3, 4, 4, 4, 5}, the mode is 4, because it appears three times, which is more than any other value.
The median is the middle value in a set of data when it is ordered in ascending or descending order. For example, if a set of data contains the values {1, 2, 3, 4, 5}, the median is 3, because it is the middle value. If there is an even number of values, then the median is the average of the two middle values.
It is important to note that different sets of data may have different measures of central tendency, and sometimes none of these measures may be appropriate.
Measures of central tendency are used to summarize and describe a set of data. The most common measures of central tendency are the mean, median, and mode.
1. Mean:
• Mean for June 2006: (508+435+538+913+367+033+254+240+137+022+160+548+260+458+358+035+222+879+136+371+127+586+201+316)/22 = $345,909
• Mean for June 2005: (422+843+469+588+245+803+199+409+132+054+139+728+254+725+345+065+210+740+134+334+125+455+184+853)/22 = $335,977
2. Median:
• Median for June 2006: Median of ordered data is the value in the middle of the data set, It is the 11th value in order set. we can see that it is $254,000
• Median for June 2005: Median of ordered data is the value in the middle of the data set, It is the 11th value in order set. we can see that it is $139,000
3. Mode:
• Mode for June 2006: There is no mode, because no value is repeated.
• Mode for June 2005: There is no mode, because no value is repeated.
Conclusions:
• The mean housing price in June 2006 is higher than the mean housing price in June
To know more about mode visit:
https://brainly.com/question/12789483
#SPJ1
11. Which of the following is the formula for the sequence 3, -6, 9, -18, 36, ... ?
A. an = 3(-2)n-1
B. an = 2(-3) -1
C. an=3(-2)"
D. an=3(2)n-1
Answers
Answer:
a
Step-by-step explanation:
K
BD bisects ZABC. Solve for x and find mZABC.
m/ABD = (6x), m/DBC = (2x+12)°
X=
m/ABC=
Answers
bisects x = -12AB / (2AB - 6BD)
m∠ABC = 6x
= 6 × (-12AB / (2AB - 6BD))
To solve for x and find the measure of angle ABC (m∠ABC), we will apply the angle bisector theorem and use the given information.
According to the angle bisector theorem, the ratio of the lengths of the segments created by an angle bisector is equal to the ratio of the measures of the angles formed by the bisector.
Let's set up the equation using the given information:
m∠ABD = 6x (angle ABD)
m∠DBC = 2x + 12 (angle DBC)
Using the angle bisector theorem, we have:
AB/BD = m∠ABD/m∠DBC
Since BD bisects ∠ABC, we can substitute the given measures into the equation:
AB/BD = (6x) / (2x + 12)
To solve for x, we can cross-multiply:
AB × (2x + 12) = BD × (6x)
Expanding both sides of the equation:
2ABx + 12AB = 6BDx
Rearranging the equation:
(2AB - 6BD)x = -12AB
Now we can isolate x:
x = -12AB / (2AB - 6BD)
The measure of angle ABC (m∠ABC), we substitute the value of x back into the expression:
Simplifying this expression further would require additional information about the lengths of AB and BD.
Without this information, we cannot find the exact value of m∠ABC.
For similar questions on bisects
https://brainly.com/question/22499006
#SPJ8
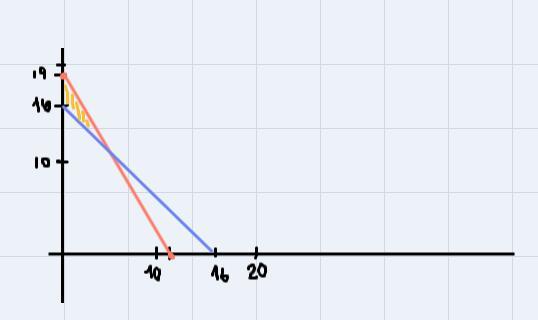
Jack is buying tables and chairs for his deck party tables cost $25 and chair cost $15 he plans to spend no more than $285 and buy at least 16 items. write a system of inequalities that meet the criteria.Graph and shade the inequalities and then list one solution that makes the situation true.
Answers
Answer:
25x + 15y ≤ 285
x + y ≥ 16
Explanation:
Let's call x the number of tables that Jack will buy and y the number of chairs that Jack will buy.
Then, the total cost for the tables will be $25 times the number of tables or $25x. In the same way, the total cost for the chairs will be $15 times the number of chairs or $15y.
So, if he plans to spend $285 or less, we can write the following inequality:
25x + 15y ≤ 285
Then, If he will buy at least 16 items, the sum of the number of tables x and the number of chairs y will be greater or equal to 16. So:
x + y ≥ 16
So, the system of inequalities that meet the criteria is:
25x + 15y ≤ 285
x + y ≥ 16
Now, to graph the inequalities we need to graph the lines that separate the regions, so we will graph the lines 25x + 15y = 285 and x + y = 16, and then we will find the region that satisfies the inequalities.
So, we will find two points in every line.
For 25x + 15y = 285, we get:
If x = 0 then:
25(0) + 15y = 285
15y = 285
y = 19
If y = 0 then:
25x + 15(0) = 285
25x = 285
x = 11.4
In the same way, for x + y = 16, we get:
If x = 0 then y = 16
If y = 0 then x = 16
So, we have (0, 19) and (11.4, 0) for the first equation and (0, 16) and (16, 0) for the second equation. Therefore, the graph of the lines is:
Where the red line is the first equation and the blue line is the second equation.
Now, we need to identify the region that satisfies the inequality, so let's select a point in every region. So, if we select the point (0, 17), we get:
25x + 15y ≤ 285
25(0) + 15(17) ≤ 285
255 ≤ 285
x + y ≥ 16
0 + 17 ≥ 16
17 ≥ 16
Since both expressions are true, this region is the solution of the system, and (0, 17) makes the situation true.
If one dozen avocados the same size weigh 7. 2 lb then what does one avocado weigh?
Answers
If one dozen avocados the same size weigh 7. 2 lb then the weight of one avocado is 0.6lb.
Weight is a measurement of the force of gravity acting on an item. It is the result of the object's mass and acceleration brought on by gravity. Usually, weight is expressed in units like pounds (lb) or kilograms (kg). Weight may be defined more simply as the amount of pressure an object applies to a scale when it is placed there. The force produced by a person's body on a scale as a result of gravity, for instance, is equal to 150 lb if they weigh 150 lb.
One dozen avocados equals 12 avocados. If one dozen avocados weigh 7.2 lb, then we can find the weight of one avocado by dividing the total weight (7.2 lb) by the number of avocados (12):
Weight of one avocado = Total weight / Number of avocados
Weight of one avocado = 7.2 lb / 12
Weight of one avocado = 0.6 lb
Therefore, the weight of one avocado is 0.6lb.
To learn more about weight, refer to:
https://brainly.com/question/86444
#SPJ4
\(\sqrt{x} 10 greater than, less than, or equal to 3\)
Answers
The square root of 10 will be greater than 3.
What is square root of a number?The square root of a number is the value which when multiplied by itself results into the number. Mathematically -
n = x²
then -
x = \(\sqrt{n}\)
Given are two numbers as -
\(\sqrt{10}\) and 3.
Now, the square root of 10 will be 3.16 (approx.)
On comparing the square root of 10 with 3, we can clearly see that the square root of 10 will be greater than 3. Mathematically -
\(\sqrt{10}\) > 3.
Therefore, we can conclude that the square root of 10 will be greater than 3.
To solve more questions on comparing numbers, visit the link below-
https://brainly.com/question/13763555
#SPJ1
a drink costs 2 dollars. a taco costs 5 dollars. given the number of each, compute total cost and assign to totalcost. ex: 2 drinks and 3 tacos yields totalcost of 19.
Answers
Answer:
To compute the total cost based on the number of drinks and tacos, we can use the given prices of $2 for a drink and $5 for a taco. Let's assume the number of drinks is represented by "d" and the number of tacos is represented by "t". The **total cost** can be calculated as:
totalcost = (2 * d) + (5 * t)
For example, if we have 2 drinks and 3 tacos, the calculation would be:
totalcost = (2 * 2) + (5 * 3) = 4 + 15 = 19
So, with 2 drinks and 3 tacos, the total cost would be $19.
You can substitute the values of "d" and "t" with the desired quantities to calculate the total cost for different combinations of drinks and tacos.
Learn more about calculations and pricing in problem-solving here:
brainly.com/question/16961791
#SPJ11
