Sample standard deviation for
283,269,259,265,256,262,268
Answers
The required sample standard deviation is approximately 8.83.
To calculate the sample standard deviation for the data set, {283, 269, 259, 265, 256, 262, 268}, follow the given steps below:
First we find the mean of the data set.
μ = (283 + 269 + 259 + 265 + 256 + 262 + 268)/7
= 266
Now, we Subtract the mean from each data value and then square it. (283 - 266)² = 289
(269 - 266)² = 9
(259 - 266)² = 49
(265 - 266)² = 1
(256 - 266)² = 100
(262 - 266)² = 16
(268 - 266)² = 4
Now, we add the squares obtained above
= (289 + 9 + 49 + 1 + 100 + 16 + 4)
= 468
Now, we divide the sum obtained by (n-1).
= (468/(7-1))
= 78
Take the square root of the quotient obtained above and we get
σ = √78 ≈ 8.83
Therefore, the sample standard deviation for the data set, {283, 269, 259, 265, 256, 262, 268} is approximately 8.83, which is the square root of the variance of the data set.
Thus, the sample standard deviation is approximately 8.83.
To know more about standard deviations,
https://brainly.com/question/475676
#SPJ11
Related Questions
3. Is it possible to find a function f(t,x) that is continuous and has continuous partial derivatives such that the functions x1(t)=tand x2(t)=sint are both solutions to x′=f(t,x) near t=0 ?
Answers
Yes, it is possible to find a function \( f(t, x) = 1 \) that is continuous and has continuous partial derivatives, making \( x_1(t) = t \) and \( x_2(t) = \sin(t) \) solutions to \( x' = f(t, x) \) near \( t = 0 \).
Certainly! We can find a function \( f(t, x) = 1 \) that satisfies the given conditions. Let's consider the differential equation \( x' = f(t, x) \), where \( x' \) represents the derivative of \( x \) with respect to \( t \). For \( x_1(t) = t \) and \( x_2(t) = \sin(t) \) to be solutions near \( t = 0 \), we need \( x_1'(t) = 1 \) and \( x_2'(t) = \cos(t) \) respectively.
Since \( f(t, x) = 1 \), it matches the derivatives of both \( x_1(t) \) and \( x_2(t) \) with respect to \( t \). The function \( f(t, x) = 1 \) is continuous and has continuous partial derivatives, making it a valid choice. Thus, \( x_1(t) = t \) and \( x_2(t) = \sin(t) \) satisfy \( x' = f(t, x) \) near \( t = 0 \).
To learn more about equation, click here:
brainly.com/question/29657983
#SPJ11
Substitute 3 for x and evaluate the expression below.
|x - 8| - 1
giving brainliest if correct and your work is shown
Answers
Answer:4
Step-by-step explanation:3-8=-5. But because it is in absolute value, it would be positive 5. And then 5-1=4.
in a random sample of 7 residents of the state of california, the mean waste recycled per person per day was 1.7 pounds with a standard deviation of 0.36 pounds. determine the 99% confidence interval for the mean waste recycled per person per day for the population of california. assume the population is approximately normal. step 1 of 2 : find the critical value that should be used in constructing the confidence interval. round your answer to three decimal places.
Answers
The critical value that should be used in constructing the confidence interval is ( 1.592, 1.807 ).
Given that;
Number of residents, n = 7
Z*- value of 90% confidence level equals z* = 0.79
Mean x = 1.7 and deviation σ = 0.36
What is the standard deviation?
Standard deviation is calculated as the square root of variance by determining each data point's deviation relative to the mean.
Now,
Number of residents, n = 7
Z*- value of 90% confidence level equals z* = 0.79
Mean x = 1.7 and deviation σ = 0.36
The confidence interval for mean waste recycled per person is
\((x-z^{*} \frac{sigma}{\sqrt{n} } ; x+z^{*} \frac{sigma}{\sqrt{n} } )\)
\((1.7 - 0.79*\frac{0.36}{\sqrt{7} } ; 1.7 + 0.79*\frac{0.36}{\sqrt{7} })\)
\((1.592, 1.807)\)
Hence, the critical value that should be used in constructing the confidence interval is ( 1.592, 1.807 ).
Learn more about the standard deviation visit:
https://brainly.com/question/12402189
#SPJ4
Which value is not a solution of the inequality -x + 5 < 7? Select all
A. 5
B.7
C. -1
D.-3
E. 10
F.-12
G. 1
H. -5
Answers
Answer:
-3
-12
-5
Step-by-step explanation:
A negative number with another negative symbol put onto it is positive because both negative symbols cancel each other out
So -(-3) = 3
-(-12) = 12
-(-5) = 5
wh at is the smallest number of rectangles, each measuring 2cm by 3cm, which are needed to fit together without overlap to form a rectangle whose sides are in the ratio 5:4 ?
Answers
The smallest number of rectangles required will be 30.
Given:- The sides of the rectangle are in the ratio of 5:4
let, length=5x
breadth=4x
Area = 20x²
Area of smaller rectangle =2*3
=6cm²
Now, take numbers which are in the ratio of 5:4;
suppose, Case 1=10:8
Case2 = 15:12
For Case 1;
number of rectangles needed =10*8/2*3
=13.3333
This means it is overlapping hence, not possible.
For Case 2;
number of rectangles needed=15*12/2*3
=30
therefore, the smallest number will be 30.
To learn more about areas of Rectangle visit;
https://brainly.com/question/20693059
#SPJ4
You run the perimeter of a baseball field at a rate of 9 feet per second.how long does it take you to run the baseball field to the nearest tenth of a second?
Answers
The answer to the nearest tenth of a second is 40.0 seconds.
To solve this problem, we need to know the length of the perimeter of a baseball field. According to official regulations, the distance between each base is 90 feet, so the perimeter of a baseball field is 360 feet.
Now, we can use the formula distance = rate x time, where distance is 360 feet, and rate is 9 feet per second. We can solve for time by dividing both sides of the equation by the rate:
time = distance / rate
time = 360 / 9
time = 40 seconds
Therefore, it takes you 40 seconds to run the perimeter of the baseball field. To find the answer to the nearest tenth of a second, we need to round the answer. Since the next decimal place after the tenths is a hundredth, we need to look at the second decimal place. If it is 5 or greater, we round up, otherwise, we round down. In this case, the second decimal place is 0, so we round down. Therefore, the answer to the nearest tenth of a second is 40.0 seconds.
Learn more on nearest tenth here:
https://brainly.com/question/12102731
#SPJ11
determine if 4x + 5 =10 and 5x + 4y = 28 is parallel or perpendicular
Answers
Answer: u have perpendicular lines
Step-by-step explanation: Hope this helps :)
if m =2 solve these 3m²-2m-7
Answers
Answer:
1
Step-by-step explanation:
m=2
3m²- 2m- 7
3(2)² -2(2) -7
3(4)- 4- 7
12- 4- 7= 1
Write the relation as a set of ordered pairs. A relation. An arrow goes from 1 to negative 1, from 2 to 0, from 3 to 1. a. ordered pairs: {(–1, 1), (2, 0), (3, 1)} b. ordered pairs: {(–1, 1), (0, 2), (1, 3)} c. ordered pairs: {(1, –1), (0, 2), (1, 3)} d. ordered pairs: {(1, –1), (2, 0), (3, 1)} Please select the best answer from the choices provided A B C D
Answers
The following ordered pair is given as {(1, -1), (2,0), (3,1)} for the given data of movement of arrow.
What is a set ?A set comprises elements or members that can be mathematical objects of any sort, including numbers, symbols, points in space, lines, other geometric forms, variables, or even other sets. A set is the mathematical model for a collection of various things.
An ordered pair consists of two items. The order of the objects in the pair matters because, unless a = b, the ordered pair differs from the ordered pair. Ordered pairs are also known as 2-tuples, or 2-length sequences.
An ordered pair is made up of the ordinate and the abscissa of the x coordinate, with two values given in parenthesis in a certain sequence. In order to understand a point visually, it might be helpful to position it on the Cartesian plane. An ordered pair's numerical values may be fractions or integers.
The following ordered pair is given as {(1, -1), (2,0), (3,1)} for the given data of movement of arrow.
To learn more about Set Theory refer to :
https://brainly.com/question/12742951
#SPJ1
Answer:
D
Step-by-step explanation:
What’s the midpoint of a line segment joining the points (5,-4) and(-13,12)?
Answers
Great question! A midpoint is exactly what it sounds like; the point in the middle of two objects (in this case it's the middle of these two coordinates). Another way to think of the middle of something in math is by using the average. To find the midpoint of two points, we just find the average of the x-values and the average of the y-values:
((x1 + x2)/2 , (y1 + y2)/2)
((5 + -13) / 2 , (-4 + 12) / 2)
( -8 / 2 , 8 / 2)
(-4 , 4)
Which is a complete list of factors of each term in the expression 15 + 20 x? 15: 1, 3, 5, 15 20x: 1, 2, 4, 5, 10, 20, x 15: 1, 3, 5, 15 20x: 1, 2, 4, 5, 10, 20 15: 3, 5 20x: 4, 5, x 15: 1, 3, 5 20x: 1, 2, 4, 5, 10, x
Answers
Answer:
15: 1 3 5 15
20: 1 2 4 5 10 20
Step-by-step explanation:
This assumes you are only factoring the coefficients of the expression. Using this assumption, we simply create a list of factors of the coefficients.
15 -> 1 * 15, 3 * 5 --> 1 3 5 15
20 -> 1 * 20, 2 * 10, 4 * 5 --> 1 2 4 5 10 20
If you don't assume factoring of just the coefficients, then 20x factors
20x: 1 2 4 5 10 20 x
Cheers.
Answer:
b
Step-by-step explanation:
amia went to a flower farm and picked f flowers. when she got home,she put the flowers in 4 vases, with 22 flowers in each vases.
'write an equation to describe this situation'
Answers
Answer:
88 Flowers
Step-by-step explanation:
The equation of a parabola is y=2x^2 +8x +3
Write the equation in vertex form and show your work.
Answers
Answer: y = 2(x + 2)² - 5
Step-by-step explanation:
We are going to use the completing the square method to transform this quadratic equation from standard form to vertex form.
Given:
y = 2x² + 8x + 3
Factor the 2 out of the first two terms:
y = 2(x² + 4x) + 3
Add and subtract \(\frac{b}{2} ^2\):
y = 2(x² + 4x + 4 - 4) + 3
Distribute the 2 into -4 and combine with the 3:
y = 2(x² + 4x + 4) - 5
Factor (x² + 4x + 4):
y = 2(x + 2)² - 5
Use mathematical induction to prove the following statements. () (1 1)" - (17) for all integers n 21. (b) If (tn) is a sequence defined recursively by t₁ = 1; n = 3n-1+4, n 22, then tn 3-2 for all integers n
Answers
(a) Base case: n = 21. Inductive step: Assume true for k, prove for k + 1. Therefore, by mathematical induction, the statement holds.(b) Base case: n = 2. Inductive step: Assume true for k, prove for k + 1. Therefore, by mathematical induction, the statement holds
(a) To prove the statement that (n^2) - (17n) holds for all integers n ≥ 21, we use mathematical induction.
Base case: For n = 21, (21^2) - (17*21) = 441 - 357 = 84, which is true.
Inductive step: Assume that the statement holds for some k ≥ 21, i.e., (k^2) - (17k) is true.
Now we need to prove it for k + 1, i.e., ((k + 1)^2) - (17(k + 1)).
Expanding and simplifying, we get (k^2) - (17k) + 2k - 17.
Using the assumption that (k^2) - (17k) holds, we substitute it and obtain 2k - 17.
Now, we need to show that 2k - 17 ≥ 0 for k ≥ 21, which is true.
Therefore, by mathematical induction, the statement (n^2) - (17n) holds for all integers n ≥ 21.
(b) To prove that tn ≤ 3 - 2 holds for all integers n ≥ 2 in the recursively defined sequence tn = 3tn-1 + 4, we use mathematical induction.
Base case: For n = 2, t2 = 3t1 + 4 = 3(1) + 4 = 7, which is less than or equal to 3 - 2.
Inductive step: Assume that the statement holds for some k ≥ 2, i.e., tk ≤ 3 - 2.
Now we need to prove it for k + 1, i.e., tk+1 ≤ 3 - 2.
Substituting the recursive formula, we have tk+1 = 3tk + 4.
Using the assumption tk ≤ 3 - 2, we get 3tk ≤ 3(3 - 2) = 3 - 2.
Adding 4 to both sides, we have 3tk + 4 ≤ 3 - 2 + 4 = 3 - 2.
Therefore, by mathematical induction, the statement tn ≤ 3 - 2 holds for all integers n ≥ 2 in the sequence tn = 3tn-1 + 4.
To learn more about mathematical induction click here brainly.com/question/31244444
#SPJ11
5(x+1)=4(x−1)+x
Someone pwease help me D:
Answers
Answer:
answer is -9
Step-by-step explanation:
5(x+1)=4(x-1)x
5x+5=4x-4+x
5x+5=4x+x-4
5x+5=5x-4
5x-5x=-4-5
x=-9
how many pounds to cups?
Answers
Answer:
2
Step-by-step explanation:
: )
Scientist tag and release a group of salmon after they hatch. Later, they catch a sample of salmon that Return To The River and check them for tags. One sample 20 out of 400 returning salmon have tags what is the best prediction of the total number of tagged salmon in a sample of 2000?
Answers
The best prediction of the number of tagged salmon in a sample of 2000 is 100.
The best prediction of the number of tagged salmon in a sample of 2000 returning salmon can be estimated using the proportion of tagged salmon in the sample of 400.
The proportion of tagged salmon in the sample of 400 is \((\frac{20}{400} )=(\frac{1}{20} )\).
According to proportion, if two sets of given numbers are increasing or decreasing in the same ratio, then the ratios are said to be directly proportional to each other. Proportions are denoted using the symbol '::' or '='.We can use this proportion:
To estimate the number of tagged salmon in a sample of 2000:
Tagged salmon in a sample of 2000 = \((\frac{1}{20}) * 2000\) = 100
Therefore, the best prediction of the number of tagged salmon in a sample of 2000 is 100.
For more such questions on prediction
https://brainly.com/question/14471838
#SPJ4
A television manufacturer has three locations where it is finally assembled. Plants a, b, and c supply 65%, 15%, and 20% respectively of the televisions used by the manufacture. Quality control has determined that 1. 5% produced by plant a are defective, while plants b and c have 2. 5% defective products. 13. What is the probability of finding a non-defective television?.
Answers
There is a 0.9815 percent chance of probability a television is not broken.
Let's assume that Plant A provides televisions = P(A) = 0.65
Let's assume that Plant B provides televisions = P(B) = 0.15
Let's assume that Plant C provides televisions = P(C) = 0.20
Also, let D = event that the television is defective
Given that it is supplied by Plant A, the likelihood that the television is malfunctioning = P(D/A) = 0.015
The probability that the television is defective given that it is supplied by Plant B = P(D/B) = 0.025
The probability that the television is defective given that it is supplied by Plant C = P(D/C) = 0.025
We will first determine the likelihood of finding a defective television before determining the likelihood of finding one without a defect.
the probability a defective television is given by;
= P(A) × P(D/A) + P(B) × P(D/B) + P(C) × P(D/C)
= 0.65 × 0.015 + 0.15 × 0.025 + 0.20 × 0.025
= 0.00975 + 0.00375 + 0.005
= 0.0185
Now, what are the chances of finding a working television = 1 - Probability of a defective television
likelihood of discovering a television that isn't broken = 1 - 0.0185
= 0.9815
Therefore, there is a 98.15% chance of finding a television that is in good condition.
To learn more about probability
https://brainly.com/question/11234923
#SPJ4
A group of mountain climbers begin an expedition with 250 pounds of food. They plan to eat a total
of 12 pounds of food per day. Write and solve a linear equation to find the number of days their
food will last.
Answers
250=12x
250/12=20.8
12/12=1
20.8 x 1 = 20.8
Answer:
y=-12x+250
If you graph it you will get that it only lasts for 20.833 days
Step-by-step explanation:
The minus twelve is the twelve pounds they eat per day, the positive 250 is the amount of food they start with. If you graph the above equation in desmos you should get the right graph if you need it. But it should last 20.833 (or just round to 21) days.
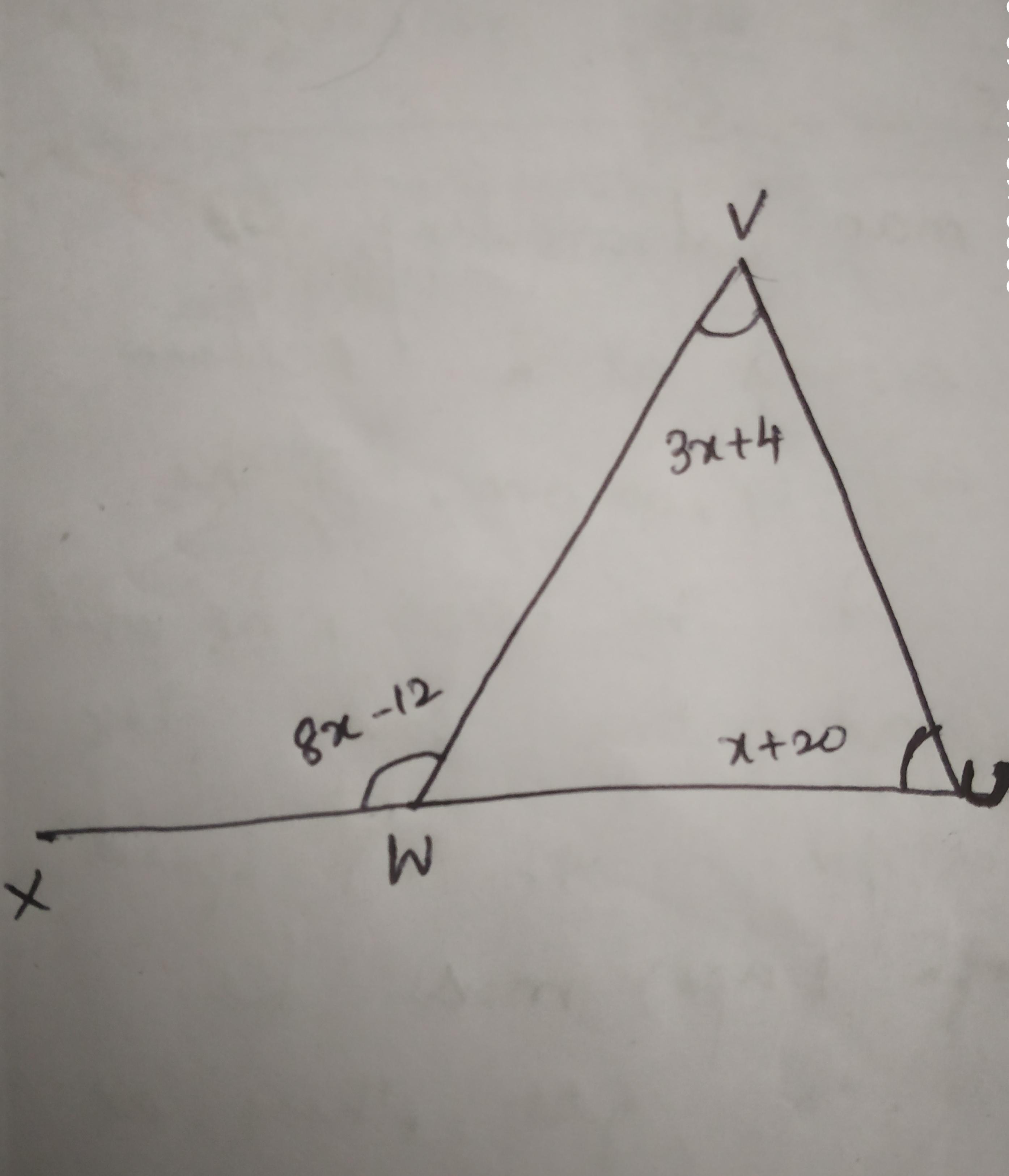
In ΔUVW,
U
W
‾
UW
is extended through point W to point X,
m
∠
U
V
W
=
(
3
x
+
4
)
∘
m∠UVW=(3x+4)
∘
,
m
∠
V
W
X
=
(
8
x
−
12
)
∘
m∠VWX=(8x−12)
∘
, and
m
∠
W
U
V
=
(
x
+
20
)
∘
m∠WUV=(x+20)
∘
. What is the value of
x
?
x?
Answers
The value of x is 9°
What do you mean by degree?
A unit of measure is used to measure the magnitude of an angle.
1 degree equals 1/360 of a complete revolution in magnitude.
Given that:
ΔUVW with side UW extended to X
m ∠UVW = (3x + 4)°
m ∠VWX = (8x -12)°
m ∠WUV = (x + 20)°
We know that ,
Sum of angles of triangle = 180°
m ∠UVW + m ∠WUV + m ∠VWU = 180°
m ∠VWU = 180° - (m ∠UVW + m ∠WUV)
Also we know that sum of angles on a straight line
m ∠VWX and m ∠VWU are supplementary angles
m ∠VWX + m ∠VWU = 180°
m ∠VWU = 180° - m ∠VWX
m ∠VWX = (m ∠UVW + m ∠WUV)
Substituting the given values , we get
(8x -12)° = (3x + 4)° + (x + 20)°
8x - 3x - x = 4 + 20 + 12
4x = 36
x = 36/4 = 9
x = 9°.
Therefore , The value of x is 9°
To learn more about degree check the given link
brainly.com/question/25770607
#SPJ1
What a deal! Just deShirts is having a 20% off sale. Trixie rushes to the store and buys 14 shirts. When the clerk rings up her purchases, Trixie sees that the clerk has added the 5% sales tax first, before taking the discount. Trixie wonders whether adding the sales tax before the discount makes her final cost more than adding the sales tax after the discount. Without making any calculations, make a conjecture. Is Trixie getting charged more when the clerk adds sales tax first? The next few problems will help you figure it out for sure.
Does it matter if sales tax is added before the discount or after her final total? (Yes or no AND why or why not?)
Answers
Answer:
no because she would get the same total if she added it before or after
Step-by-step explanation:
Kendo opened a beverage booth at the local flea market and sold 200 drinks last weekend. The pie chart depicts the proportio sold compared to lce teas. 2 times as many 4.5 times as many 1.5 times as many 3.5 times as many
Answers
The pie chart represents the proportions of different types of drinks sold at Kendo's beverage booth. The proportions are as follows: 2 times as many of one type, 4.5 times as many of another type, 1.5 times as many of another type, and 3.5 times as many of another type.
Based on the information provided, we can interpret the pie chart as showing the relative quantities of different types of drinks sold at Kendo's beverage booth. Let's assign variables to represent the quantities of each type of drink.
Let's say the quantity of the first type of drink is x. According to the pie chart, the second type of drink is sold in 2 times as many quantities, so its quantity would be 2x. Similarly, the third type of drink is sold in 4.5 times as many quantities, so its quantity would be 4.5x. The fourth type of drink is sold in 1.5 times as many quantities, making its quantity 1.5x. Finally, the fifth type of drink is sold in 3.5 times as many quantities, so its quantity is 3.5x.
To find the exact quantities of each type of drink, we need additional information or values. The given information only states the proportional relationships between the quantities.
Learn more about pie chart here:
https://brainly.com/question/29148468
#SPJ11
Can someone please help me with this? I am not good at Algebra
Reward: 2 ppl answer 1s person gets a brainly, thanks on ur page, and a follow
Wrong Answers will get reported and so will nonsense

Answers
Let theta be an angle such that cos(theta) = -1/9 and 0 <=theta<=2pi
Assume that cos(theta/2) < 0. Then if
Terminal point of theta/2 = (a1, a2), enter a1 and a2 in that order.
Answers
In this case, the terminal point of theta/2 can be determined using the following steps:
Since cos(theta/2) < 0 and the cosine function has a range of [-1, 1], it follows that theta/2 must be in the second or third quadrant (90 degrees to 180 degrees or 180 degrees to 270 degrees).
To find the terminal point of theta/2, we can use the formula for converting from polar to Cartesian coordinates: x = rcos(theta) and y = rsin(theta), where (x,y) is the Cartesian coordinates of the terminal point, r is the radius, and theta is the angle in radians.
In this case, the radius is 1 (since the terminal point is on the unit circle) and the angle is theta/2. Substituting these values into the formulas above, we get:
x = 1 * cos(theta/2)
y = 1 * sin(theta/2)
To find the values of cos(theta/2) and sin(theta/2), we can use the identity cos(theta/2) = sqrt((1 + cos(theta))/2) and sin(theta/2) = sqrt((1 - cos(theta))/2).
Substituting the given value of cos(theta) (-1/9) and the identities above into the formulas for x and y, we get:
x = sqrt((1 + (-1/9))/2) = -sqrt(2)/3
y = sqrt((1 - (-1/9))/2) = sqrt(8)/3
Thus, the coordinates of the terminal point of theta/2 are (-sqrt(2)/3, sqrt(8)/3).
The terminal point (a₁, a₂) for theta/2 is (-2/3, √(5) / 3).
How to find terminal point?To find the terminal point (a₁, a₂) of theta/2, use the half-angle identity for cosine:
cos(theta/2) = ± √((1 + cos(theta)) / 2)
Given that cos(theta) = -1/9 and cos(theta/2) < 0, the negative sign should be used in the half-angle identity.
Calculate cos(theta/2):
cos(theta/2) = - √((1 + cos(theta)) / 2)
cos(theta/2) = - √((1 - 1/9) / 2)
cos(theta/2) = - √((8/9) / 2)
cos(theta/2) = - √(8/18)
cos(theta/2) = - √(4/9)
cos(theta/2) = - 2/3
Cos(theta/2) = -2/3. To find the terminal point (a₁, a₂), determine the values of a₁ and a₂.
Since cos(theta/2) is negative, a₁ is negative. To find the value of a₂, use the Pythagorean identity:
cos²(theta/2) + sin²(theta/2) = 1
Since cos(theta/2) = -2/3, calculate sin(theta/2):
sin²(theta/2) = 1 - cos²(theta/2)
sin²(theta/2) = 1 - (-2/3)²
sin²(theta/2) = 1 - 4/9
sin²(theta/2) = 5/9
sin(theta/2) = ± √(5/9)
sin(theta/2) = ± √(5) / 3
Since theta is in the second quadrant (cos(theta) = -1/9), sin(theta) is positive in the second quadrant. Therefore, sin(theta/2) = √(5) / 3.
Now, sin(theta/2) = √(5) / 3.
So, the terminal point (a₁, a₂) for theta/2 is (-2/3, √(5) / 3).
Find out more on Terminal point here: https://brainly.com/question/14435471
#SPJ2
Ms. Rowlen went Black Friday shopping and she bought a flat screen TV that originally costs $259.00. She used her super savings coupon of 45%, how much did Ms. Rowlen pay for the tv?
Answers
Answer:
142.55
Step-by-step explanation:
What four adjacent square numbers have a diagonal sum of 161? what four adjacent square numbers have a diagonal sum of 45? what three adjacent vertical numbers add up to 156?
Answers
The four adjacent square numbers with a diagonal sum of 45 are 2^2, 3^2, 4^2, and 5^2, which are 4, 9, 16, and 25.
To find the four adjacent square numbers with a diagonal sum of 161, we can start by considering the square numbers. Let's call the four numbers x^2, (x+1)^2, (x+2)^2, and (x+3)^2. The diagonal sum can be expressed as: x^2 + (x+1)^2 + (x+2)^2 + (x+3)^2 = 161. Simplifying the equation: x^2 + (x^2 + 2x + 1) + (x^2 + 4x + 4) + (x^2 + 6x + 9) = 161; 4x^2 + 12x + 14 = 161; 4x^2 + 12x - 147 = 0. Using the quadratic formula, we can solve for x: x = (-12 ± √(12^2 - 44(-147))) / (2*4); x = (-12 ± √(144 + 2352)) / 8; x = (-12 ± √2496) / 8
x = (-12 ± 49.96) / 8. Solving for x, we have two possible solutions: x = 4 or x ≈ -9.496. Since we are looking for positive square numbers, we can discard the negative solution. Therefore, the four adjacent square numbers with a diagonal sum of 161 are 4^2, 5^2, 6^2, and 7^2, which are 16, 25, 36, and 49.
To find the four adjacent square numbers with a diagonal sum of 45, we can follow the same approach. The equation would be: x^2 + (x+1)^2 + (x+2)^2 + (x+3)^2 = 45. Simplifying this equation and solving for x, we find that x = 2. Therefore, the four adjacent square numbers with a diagonal sum of 45 are 2^2, 3^2, 4^2, and 5^2, which are 4, 9, 16, and 25. To find three adjacent vertical numbers that add up to 156, we need more information about the arrangement of the numbers. Please provide additional details or context about the arrangement of the numbers so that we can solve the problem accurately.
To learn more about diagonal sum click here: brainly.com/question/1400844
#SPJ11
please help people are bringing me down with all these files this is my 5th time asking so please.

Answers
Answer:
b.16
hope this helps
\('-' )/
Clint is interested in making an offer on a house with hardwood floors that will need to be replaced. The hallway is 18 feet by 6 feet. The kitchen is 20 feet by 30 feet. The living room is 25 feet by 45 feet. There are two bedrooms, which measure 12 feet by 16 feet each, plus a master bedroom that is 14 feet by 20 feet. If the cost of the flooring is $5.48 per square foot, and the cost of installation is $1.49 per square foot, how much can Clint plan to spend to replace the floors
Answers
The amount of money Clint will plan to spend to replace the floors is $17404.09
How to find the cost to replace the floor?The hardwood floor is rectangular.
Therefore,
area of hallway = 18 × 6 = 108 ft²
area of the kitchen = 20 × 30 = 600 ft²
area of the living room = 25 × 45 = 1125 ft²
area of each bedroom = 12 × 16 = 192 ft²
area of master bedroom = 14 × 20 = 280 ft²
Hence,
cost of flooring per square foot is $5.48
total cost for flooring = 108(5.48) + 600(5.48) + 1125(5.48) + 192(5.48) + 192(5.48) + 280(5.48) = $13683.56
Cost of installation is $1.49 per square.
total cost of installation = 108(1.49) + 600(1.49) + 1125(1.49) + 192(1.49) + 192(1.49) + 280(1.49) = $3720.53
Total amount to replace the floor = 13683.56 + 3720.53 = $17404.09
Learn more about cost at: brainly.com/question/21394250
#SPJ4
we have a study involving 3 different groups that each contain 9 participants (27 total). what two degrees of freedom would we report when we report the results of our study?
Answers
Using degree of freedom,
Two degrees of freedom would we report when we report the results of our study is (2,24).
Degree of freedom:
The statistical degrees of freedom (DF) indicate the number of independent values that can be changed in the analysis without violating the constraints.
degrees of freedom is the number of independent values that can be estimated in a statistical analysis. It can also be thought of as the number of values that are free to vary when estimating the parameters
DF = N – P
Where:
N = sample size
P = the number of relationships
We given that,
Number of groups , k = 3
Number of total participants, n = 27
Degrees of freedom for F-test is F(k-1,n-k)
= F(3-1 , 27-3)
= F(2,24)
Hence, (2,24,) are required two degrees of freedom.
To learn more about degree of freedom in statistics, refer:
#SPJ4
Sal's Plumbing charges $25 for a service call plus $50 per hour of service. Write the equation.
:: y = 50x - 25
#: y = 50x + 25
y = -50x + 25

Answers
Answer: y = $50x + $25
Step-by-step explanation:
First, let x be equal to the hours of service and y be the total cost. Since the cost is 50 dollars per hour of service, we will write this as "y = 50x" for our equation.
Next, there is a 25-dollar charge for each call. We will add this to our equation as "y = 50x + 25."
Our equation is;
y = $50x + $25