Answers
The probability of a junior not playing a sport given that they do not have a gym membership is 45/102, which is about 0.4412 or 44.1% rounded to the tenths place.
What is probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen.
To find the probabilities, we can use the formula:
P(A | B) = P(A and B) / P(B)
where P(A | B) is the probability of A given that B has occurred, P(A and B) is the probability of A and B occurring together, and P(B) is the probability of B occurring.
Using this formula, we can calculate the probabilities:
a. P(membership | sport)
P(membership and sport) = 57 (the number of juniors who have a gym membership and play a sport)
P(sport) = 57 + 41 = 98 (the total number of juniors who play a sport)
P(membership | sport) = P(membership and sport) / P(sport) = 57/98
Therefore, the probability of a junior having a gym membership given that they play a sport is 57/98, which is about 0.5816 or 58.2% rounded to the tenths place.
b. P(no sport | no membership)
P(no sport and no membership) = 45 (the number of juniors who have no gym membership and do not play a sport)
P(no membership) = 45 + 57 = 102 (the total number of juniors who do not have a gym membership)
P(no sport | no membership) = P(no sport and no membership) / P(no membership) = 45/102
Therefore, the probability of a junior not playing a sport given that they do not have a gym membership is 45/102, which is about 0.4412 or 44.1% rounded to the tenths place.
To learn more about probability from the given link:
https://brainly.com/question/30034780
#SPJ1
Related Questions
Sixth grade
Jacob is planting flowers for his grandmother. This morning, he spent an hour planting
annuals and an hour planting perennials, but he planted more annuals than perennials. This
afternoon, he has the same number of annuals and perennials left to plant. Which will likely
take him more time to plant?
Answers
Step-by-step explanation:
Guess "This afternoon l,he has the same number of annuals and perennials left to plant will take more time to plant.
NO LINKS!! Please help me with these problems. Part 13a1

Answers
Answer's:
27. vertex: (-4, -5) and x-intercept: (√5 - 4, 0) and (-√5 - 4, 0)
28. vertex: (-5, -11) and x-intercept: (√11 - 5, 0) and (-√11 - 5, 0)
29. vertex: (1, 16) and x-intercept: (-3, 0) and (5, 0)
To find vertex, the quadratic function should be in f(x) = a(x - h)² + k form.
where:
(h, k) is the vertex27.
g(x) = x² + 8x + 11
completing square:
g(x) = (x² + 8x) + 11
g(x) = (x + 4)² + 11 - (4)²
g(x) = (x + 4)² - 5
g(x) = (x - (-4))² - 5
To find x-intercept: set y = 0
\(\sf (x + 4)^2 - 5 = 0\)
\(\sf (x + 4)^2 = 5\)
\(\sf x + 4 = \pm \sqrt{5}\)
\(\sf x= \sqrt{5}-4, \ - \sqrt{5}-4\)
Hence, the vertex is (-4, -5) and x intercepts (√5 - 4, 0) and (-√5 - 4, 0).
28.
f(x) = x² + 10x + 14
completing square:
f(x) = (x² + 10x) + 14
f(x) = (x + 5)² + 14 - (5)²
f(x) = (x + 5)² - 11
Find x intercept, so y = 0:
\(\sf (x + 5)^2 - 11 = 0\)
\(\sf (x + 5)^2 = 11\)
\(\sf x + 5 = \pm\sqrt{11}\)
\(\sf x = \sqrt{11} -5, \ -\sqrt{11} -5\)
Hence, the vertex is (-5, -11) and x intercepts (√11 - 5, 0) and (-√11 - 5, 0).
29.
f(x) = -(x² - 2x - 15)
f(x) = -((x² - 2x)) + 15
f(x) = -(x - 1)² + 15 + (-1)²
f(x) = -(x - 1)² + 16
Find the x-intercept's:
\(\sf -(x - 1)^2 + 16 = 0\)
\(\sf -(x - 1)^2 = -16\)
\(\sf (x - 1)^2 = 16\)
\(\sf x - 1 = \pm\sqrt{16}\)
\(\sf x - 1 = \pm4\)
\(\sf x = -3, \ 5\)
Hence, the vertex is (1, 16) and x intercepts (-3, 0) and (5, 0).



Answer:
\(\textsf{27.} \quad \textsf{Vertex}:(-4,-5) \quad \textsf{$x$-intercepts}: x=-4+\sqrt{5}, \:\:x=-4-\sqrt{5}\)
\(\textsf{28.} \quad \textsf{Vertex}:(-5,-11) \quad \textsf{$x$-intercepts}: x = -5+\sqrt{11}, \:\:x=-5-\sqrt{11}\)
\(\textsf{29.} \quad \textsf{Vertex}:(1,16) \quad \textsf{$x$-intercepts}: x = 5, \:\:x=-3\)
Step-by-step explanation:
Vertex form of a quadratic function:
\(\boxed{y=a(x-h)^2+k}\)
where:
(h, k) is the vertex.\(a\) is some constant.Question 27Given function:
\(g(x)=x^2+8x+11\)
Change to vertex form by completing the square.
Add and subtract the square of half the coefficient of x:
\(\implies g(x)=x^2+8x+11 +\left(\dfrac{8}{2}\right)^2-\left(\dfrac{8}{2}\right)^2\)
\(\implies g(x)=x^2+8x+11 +16-16\)
\(\implies g(x)=x^2+8x+16+11-16\)
\(\implies g(x)=x^2+8x+16-5\)
Factor the perfect trinomial:
\(\implies g(x)=(x+4)^2-5\)
Therefore, the vertex is (-4, -5).
To find the x-intercepts, set the function to zero and solve for x:
\(\begin{aligned}g(x) & = 0\\\implies (x+4)^2 -5 & = 0\\(x+4)^2 & = 5\\\sqrt{(x+4)^2} & = \sqrt{5}\\x+4&=\pm\sqrt{5}\\x+4-4&=-4\pm\sqrt{5}\\x&=-4\pm\sqrt{5}\end{aligned}\)
Therefore, the x-intercepts are:
\(x = -4+\sqrt{5}, \quad x = -4-\sqrt{5}\)
---------------------------------------------------------------------
Question 28Given function:
\(f(x)=x^2+10x+14\)
Change to vertex form by completing the square.
Add and subtract the square of half the coefficient of x:
\(\implies f(x)=x^2+10x+14+\left(\dfrac{10}{2}\right)^2-\left(\dfrac{10}{2}\right)^2\)
\(\implies f(x)=x^2+10x+14+25-25\)
\(\implies f(x)=x^2+10x+25+14-25\)
\(\implies f(x)=x^2+10x+25-11\)
Factor the perfect trinomial:
\(\implies f(x)=(x+5)^2-11\)
Therefore, the vertex is (-5, -11).
To find the x-intercepts, set the function to zero and solve for x:
\(\begin{aligned}f(x) & = 0\\\implies (x+5)^2 -11 & = 0\\(x+5)^2 & = 11\\\sqrt{(x+5)^2} & = \sqrt{11}\\x+5&=\pm\sqrt{11}\\x+5-5&=-5\pm\sqrt{11}\\x&=-5\pm\sqrt{11}\end{aligned}\)
Therefore, the x-intercepts are:
\(x = -5+\sqrt{11}, \quad x = -5-\sqrt{11}\)
---------------------------------------------------------------------
Question 29Given function:
\(f(x)=-(x^2-2x-15)\)
Change to vertex form by completing the square.
Add and subtract the square of half the coefficient of x:
\(f(x)=-\left(x^2-2x-15+\left(\dfrac{-2}{2}\right)^2-\left(\dfrac{-2}{2}\right)^2\right)\)
\(f(x)=-\left(x^2-2x-15+1-1\right)\)
\(f(x)=-\left(x^2-2x+1-15-1\right)\)
\(f(x)=-\left(x^2-2x+1-16\right)\)
Factor the perfect trinomial:
\(f(x)=-\left((x-1)^2-16\right)\)
Simplify:
\(f(x)=-(x-1)^2+16\)
Therefore, the vertex is (1, 16).
To find the x-intercepts, set the function to zero and solve for x:
\(\begin{aligned}f(x) & = 0\\\implies -(x-1)^2 +16 & = 0\\(x-1)^2 -16 & = 0\\(x-1)^2 & = 16\\\sqrt{(x-1)^2} & = \sqrt{16}\\x-1&=\pm4\\x-1+1&=1\pm4\\x&=5,-3\end{aligned}\)
Therefore, the x-intercepts are:
\(x = 5, \quad x=-3\)
What is the domain of the function shown on the graph?

Answers
The asnwer is C
for finding domain look at just x-axis from left to right , because there are arrows , so domain is all real numbers or from negative infinity to positive infinity
Please give brainliest
Another day, another math problem 3

Answers
Answer:
\(2\sqrt{x+1}-3\\domain:[-1, \infty)\)
Step-by-step explanation:
\(g(h(x)) = 2(\sqrt{x+1})-3\\g(h(x)) = 2\sqrt{x+1} - 3\\\)
the function is only defined when (x+1) >= 0 (since square root) so the domain is when x >= -1
Show that the equations x+y+z = 4, 2x+5y-2z =3, x+7y-7z =5 are not consistent
Answers
Answer:
We can start by using the second equation to eliminate x:
2x + 5y - 2z = 3
2x = -5y + 2z + 3
x = (-5/2)y + z + 3/2
Now we can substitute this expression for x into the first and third equations:
x + y + z = 4
(-5/2)y + z + 3/2 + y + z = 4
(-5/2)y + 2z = 5/2
x + 7y - 7z = 5
(-5/2)y + z + 3/2 + 7y - 7z = 5
(9/2)y - 6z = 7/2
Now we have a system of two equations with two variables, (-5/2)y + 2z = 5/2 and (9/2)y - 6z = 7/2. We can use any method to solve for y and z, such as substitution or elimination. However, we will find that the system is inconsistent, meaning there is no solution that satisfies both equations.
Multiplying the first equation by 9 and the second equation by 5 and adding them, we get:
(-45/2)y + 18z = 45/2
(45/2)y - 30z = 35/2
Adding these two equations, we get:
-12z = 40/2
-12z = 20
z = -5/3
Substituting z = -5/3 into (-5/2)y + 2z = 5/2, we get:
(-5/2)y + 2(-5/3) = 5/2
(-5/2)y - 10/3 = 5/2
(-5/2)y = 25/6
y = -5/12
Substituting y = -5/12 and z = -5/3 into any of the original equations, we get:
x + y + z = 4
x - 5/12 - 5/3 = 4
x = 29/12
Therefore, the solution is (x, y, z) = (29/12, -5/12, -5/3). However, if we substitute these values into any of the original equations, we will find that it does not satisfy the equation. For example:
2x + 5y - 2z = 3
2(29/12) + 5(-5/12) - 2(-5/3) = 3
29/6 - 5/2 + 5/3 ≠ 3
Since there is no solution that satisfies all three equations, the system is inconsistent.
Step-by-step explanation:
Answer:
See below for proof.
Step-by-step explanation:
A system of equations is not consistent when there is no solution or no set of values that satisfies all the equations simultaneously. In other words, the equations are contradictory or incompatible with each other.
Given system of equations:
\(\begin{cases}x+y+z = 4\\2x+5y-2z =3\\x+7y-7z =5\end{cases}\)
Rearrange the first equation to isolate x:
\(x=4-y-z\)
Substitute this into the second equation to eliminate the term in x:
\(\begin{aligned}2x+5y-2z&=3\\2(4-y-z)+5y-2z&=3\\8-2y-2z+5y-2z&=3\\-2y-2z+5y-2z&=-5\\5y-2y-2z-2z&=-5\\3y-4z&=-5\end{aligned}\)
Subtract the first equation from the third equation to eliminate x:
\(\begin{array}{cccrcrcl}&x&+&7y&-&7z&=&5\\\vphantom{\dfrac12}-&(x&+&y&+&z&=&4)\\\cline{2-8}\vphantom{\dfrac12}&&&6y&-&8z&=&1\end{aligned}\)
Now we have two equations in terms of the variables y and z:
\(\begin{cases}3y-4z=-5\\6y-8z=1\end{cases}\)
Multiply the first equation by 2 so that the coefficients of the variables of both equations are the same:
\(\begin{cases}6y-8z=-10\\6y-8z=1\end{cases}\)
Comparing the two equations, we can see that the coefficients of the y and z variables are the same, but the numbers they equate to is different. This means that there is no way to add or subtract the equations to eliminate one of the variables.
For example, if we subtract the second equation from the first equation we get:
\(\begin{array}{crcrcl}&6y&-&8z&=&-10\\\vphantom{\dfrac12}-&(6y&-&8z&=&\:\:\;\;\:1)\\\cline{2-6}\vphantom{\dfrac12}&&&0&=&-11\end{aligned}\)
Zero does not equal negative 11.
Since we cannot eliminate the variable y or z, we cannot find a unique solution that satisfies all three equations simultaneously. Therefore, the system of equations is inconsistent.
PLEASE ANSWER THIS I HAVE 5 MINS WILL MARK BRAINLIEST IF CORRECT (PICTURE)

Answers
A= 36 * 3.14
A = 113.04 but after rounding the answer will be 113 cm^2
Answer:
Step-by-step explanation:
diameter = 12 cm
r = 12/2 = 6 cm
\(Area \ of \ semicircle = \dfrac{1}{2}\pi r^{2}\\\\\\=\dfrac{1}{2}* 3.14*6*6\\\\\\= 56.52 \ cm^{2}\)
Anna volunteers on the weekend at the Central Library. As a school project, she decides to record how many people visit the library, and where they go. On Saturday, 382 people went to The Youth Wing, 461 people went to Social Issues, and 355 went to Fiction and Literature. On Sunday, the library had 800 total visitors. Based on what Anna had recorded on Saturday, about how many people should be expected to go to The Youth Wing? Round your answer to the nearest whole number.
Answers
Based on the data recorded by Anna on Saturday, we can estimate the number of people expected to visit The Youth Wing on Sunday.
Let's calculate the proportion of visitors to The Youth Wing compared to the total number of visitors on Saturday:
\(\displaystyle \text{Proportion} = \frac{\text{Visitors to The Youth Wing on Saturday}}{\text{Total visitors on Saturday}} = \frac{382}{382 + 461 + 355}\)
Next, we'll apply this proportion to the total number of visitors on Sunday to estimate the number of people expected to go to The Youth Wing:
\(\displaystyle \text{Expected visitors to The Youth Wing on Sunday} = \text{Proportion} \times \text{Total visitors on Sunday}\)
Now, let's substitute the values into the equation and calculate the estimated number of visitors to The Youth Wing on Sunday:
\(\displaystyle \text{Proportion} = \frac{382}{382 + 461 + 355}\)
\(\displaystyle \text{Expected visitors to The Youth Wing on Sunday} = \text{Proportion} \times 800\)
Calculating the proportion:
\(\displaystyle \text{Proportion} = \frac{382}{382 + 461 + 355} = \frac{382}{1198}\)
Calculating the estimated number of visitors to The Youth Wing on Sunday:
\(\displaystyle \text{Expected visitors to The Youth Wing on Sunday} = \frac{382}{1198} \times 800\)
Simplifying the equation:
\(\displaystyle \text{Expected visitors to The Youth Wing on Sunday} \approx \frac{382 \times 800}{1198}\)
Now, let's calculate the approximate number of visitors to The Youth Wing on Sunday:
\(\displaystyle \text{Expected visitors to The Youth Wing on Sunday} \approx 254\)
Therefore, based on the data recorded on Saturday, we can estimate that around 254 people should be expected to go to The Youth Wing on Sunday.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
If the fabric, thread, buttons, and zipper cost $13.30, how much is the sales tax if the tax is 8%?
Answers
Answer:
it'd be $1.06 rounded to the nearest thousendth or $1.06400
Step-by-step explanation:
13.30*8/100=Your Answer
Increase £16470.45 by 3.5%
Give your answer rounded to 2 DP
Answers
Answer:
it is £16490.36
Step-by-step explanation:
since £156.78 is 100%, £16470.45 by 3.5 is £16490.36
Answer:
it's 17,046.92
Step-by-step explanation:
that's what my calculations said
If AIf C=2a² - 5 and D = 3 -a, then C - 2D equals2a2 + a-82)2a283) 2a² + 2a - 112a2-a-111)2)
Answers
4) 2a²+a -11
1) If C = 2a²-5 and D = 3-a, then C -2D =?
2) D = 3-a
a=3-D Writing that for a
C -2D Plugging into C and D
2a² -5 - 2(3-a) Applying distributive property
2a²-5 -6 +a Combining like terms
2a² -11 +a
2a²+a -11
Penelope goes out to lunch. The bill, before tax and tip, was $16.05. A sales tax of 3% was added on. Penelope tipped 18% on the amount after the sales tax was added. How much tip did she leave? Round to the nearest cent.
Answers
Answer:
2.98
Step-by-step explanation:
First find 3% of 16.05 which is 0.48.
Then add 0.48 to 16.05 which is 16.53.
Then multiply .18 by 16.53 which gets you 2.98
Hope it helps
Answer:
To find the amount of the sales tax, we need to multiply the bill amount by the tax rate of 3% or 0.03:
Sales tax = 0.03 x $16.05 = $0.48
To find the total amount of the bill after the sales tax was added, we need to add the bill amount to the sales tax:
Total bill = $16.05 + $0.48 = $16.53
To find the amount of the tip, we need to calculate 18% of the total bill after the sales tax was added:
Tip = 0.18 x $16.53 = $2.98
Rounding to the nearest cent, Penelope left a tip of $2.98.
Step-by-step explanation:
. Find the greatest common factor and the least common multiple of each of the following sets of numbers. 12 and 7
Answers
Answer:
HCF: 1
LCM: 84
Step-by-step explanation:
7 is a prime number. Nothing but 1 and 7 divide into which means that twelve and 7 have no highest common factor but 1.
The lowest common multiply (because 12 and 7 are prime to each other ) is 12 * 7 = 84
Answer:
LCM = 84 GCF = 1
Step-by-step explanation:
LCM of 7 and 12 is 84.
GCF(7,12) = 1
LCM(7,12) = ( 7 × 12) / 1
LCM(7,12) = 84 / 1
LCM(7,12) = 84
The formula of LCM is LCM(a,b) = ( a × b) / GCF(a,b).
GCF of 7 and 12 is 1. Now calculate the prime factors of 7 and 12, then find the greatest common factor (greatest common divisor) of the numbers.
To find the GCF of two numbers: List the prime factors of each number. Multiply those factors both numbers have in common. If there are no common prime factors, the GCF is 1.
At a family reunion, there only blood relatives, consisting of children, parents, and grandparents, in attendance. There were 400 people total. There were twice as many parents as grandparents, and 50 more children than parents. How many children, parents, and Grandparents were in attendance?
Applying the Solution to a 3X3 System
Show up all steps please
Answers
our equation now looks like
y = 2z, x=y+50 and xty+z= 400.
× = 190
y= 140
z= 70
Show how you got each answer:
What is the measurement of ∟1 if gg || h?
What is the measurement of ∟3 if gg || h?

Answers
Step-by-step explanation:
angles 1 and 3 are supplementary angles (together they have 180°), because together they make sure that line f is a straight line, and there are no segments of the line angling "off". a straight line can be always seen as prolonged diameter of a circle. each side represents a half-circle with 180°.
a line intersecting 2 parallel lines has the same intersection angles with both lines, as parallel lines perfectly copy each other's behavior and attributes except for the y-intercept.
the angles of intersecting lines are the same in both sides of any of the 2 lines, they are just left-right mirrored.
therefore,
angle 1 = 82° = angle 2
angle 3 = 180 - angle 1 = 180 - 82 = 98° = angle 4
Answer:
∠1 = 82°
∠3 = 98°
Step-by-step explanation:
You want the measures of angles 1 and 3 where a transversal crosses parallel lines and one of the angles is marked as 82°.
Alternate interior anglesThe "alternate interior angles theorem" tells you that the alternate interior angles created by a transversal crossing parallel lines are congruent. Hence angle 1 is congruent to the one marked 82°.
∠1 = 82°
Linear pairThe angles of a linear pair are supplementary. Angles 1 and 3 form a linear pair, so ...
∠3 = 180° -∠1 = 180° -82°
∠3 = 98°
__
Additional comment
"Interior" angles are between the parallel lines. "Exterior" angles are outside the parallel lines. "Alternate" angles are on opposite sides of the transversal. "Consecutive" or "same-side" angles are on the same side of the transversal. (Angles 2 and 4 are "consecutive".)
"Corresponding" angles are in the same direction from the point of intersection of the transversal with the parallel lines. In this figure, angle 2 and the one marked 82° are corresponding. Corresponding angles are congruent. If you remember that, and that vertical angles are congruent, and linear pairs are supplementary, you can figure out all of the other relationships.
In the end, when the lines are parallel, all of the acute angles are congruent, and all of the obtuse angles are congruent. The acute and obtuse angles are supplementary. The angle relations themselves are pretty simple; the rest is a lot of vocabulary.
If you are god of math you can try this

Answers
Answer:
BRO, u dont need to be a god :D, This is simple math and you just need to use your brains
Step-by-step explanation:
Given is a polynomial, and the values of the variables in it are given by showing what set are they an element of, right? It just gets easier from here
They tell us that 'z' is an element of set C, which stands for Complex Numbers.
And they also tell us that 'a' is an element of set Z, which stands for Integers, which are just numbers with a sign :).
They have also given us a root (solution) to the polynomial, which is also a complex number.
The two statements given are just there for us to verify that we are on the right track to the solution.
We can see that (z = 3 + i) which of course is a complex number, due to the presence of 'i', and 'a' is an integer for when we find its value.
Put it all together and we will get the answer.
Like this,
take the given value of 'z' and place it into the polynomial given, now keep your eyes open here. They said the value of z is as such when the polynomial is an equation which equals 0, so hence we get this:
P(z) = a(3+i)³ - 37(3+i)² + 66(3+i) - 10 = 0,
now just go on simplifying,
=> a(3³+i³+3×3²i+3×3i²) - 37(3²+2×3×i+i²) + 66×3 + 66×i - 10 = 0
=> a(27-i+27i-9i) - 37(9+6i-1) + 198 + 66i - 10 = 0
=> a(27+17i) - 37(8+6i) + 188 + 66i = 0
=> a(27+17i) = 296 + 222i - 188 - 66i
=> a(27+17i) = 108 + 156i
=> a = (108+156i) / (27+17i)
=> a = (108+156i)(27-17i) / (27)² - (17i)²
=> a = (5568 + 2376i) / (699 + 289)
=> a = 5568 + 2376i / 1488
DONNEEE....yayyyy....lol
The product of two fractions is 2/1/2 if one of the fraction is 7/1/2 find the other
Answers
Then, we have:
7/ 1/2 . x
= 2 / 1/2
Simplifying the left-hand side, we get:
7x = 4
Dividing both sides by 7, we get:
x = 4/7
Therefore, the other fraction is
4/7
The radius of the base of a cylinder is expanding at a constant rate of 3 mm/min. If the height of
the cylinder is a constant 20 mm, find the rate at which the VOLUME of the cylinder is changing at the
moment when the radius of the base of the cylinder is 10 mm. Also find the rate at which the SURFACE
AREA of the cylinder is changing at this same moment.
(V = r²h, SA=2лrh+2rr²)
I’m getting 1800pi mm^3/min for volume and 360pi mm^2/min for surface area but I’m not sure if it’s correct
Answers
The rate at which the volume of the cylinder is changing is 600 mm^3/min, and the rate at which the surface area is changing is 240π mm^2/min.
To find the rate at which the volume and surface area of the cylinder are changing, we can use the given formulas for volume and surface area and differentiate them with respect to time. Let's calculate the rates at the moment when the radius of the base is 10 mm.
Given:
Radius rate of change: dr/dt = 3 mm/min
Height: h = 20 mm
Radius: r = 10 mm
Volume of the cylinder (V) = \(r^2h\)
Differentiating with respect to time (t), we have:
dV/dt = 2rh(dr/dt) + \(r^2\)(dh/dt)
Since the height of the cylinder is constant, dh/dt = 0.
Substituting the given values:
dV/dt = 2(10)(20)(3) + (10^2)(0)
dV/dt = 600 + 0
dV/dt = 600 mm^3/min
Therefore, the rate at which the volume of the cylinder is changing at the given moment is 600 mm^3/min.
Surface area of the cylinder (SA) = 2πrh + 2π\(r^2\)
Differentiating with respect to time (t), we have:
dSA/dt = 2πr(dh/dt) + 2πh(dr/dt) + 4πr(dr/dt)
Again, since the height of the cylinder is constant, dh/dt = 0.
Substituting the given values:
dSA/dt = 2π(10)(0) + 2π(20)(3) + 4π(10)(3)
dSA/dt = 0 + 120π + 120π
dSA/dt = 240π mm^2/min
Therefore, the rate at which the surface area of the cylinder is changing at the given moment is 240π mm^2/min.
For more such questions on cylinder
https://brainly.com/question/28247116
#SPJ8
Consumers Energy states that the average electric bill across the state is $67.16. You want to test the claim that the average bill amount is greater than $67.16. The hypotheses for this situation are Null Hypothesis: μ ≤ 67.16, Alternative Hypothesis: μ > 67.16. If the true statewide average bill is $51.28 and the null hypothesis is not rejected, did a type I, type II, or no error occur?
a. Type I Error has occured.
b. No error has occured.
c. We do not know the degrees of freedom, so we cannot determine if an error has occured.
d. Type II Error has occured
e. We do not know the p-value, so we cannot determine if an error has occured.
Answers
Answer:
B: No error has occured
Step-by-step explanation:
In statistical hypothesis testing, we have two types of errors namely Type I error and Type II error.
Type I error occurs when we reject the null hypothesis although it is true. Meanwhile, Type II error occurs when we fail to reject the null hypothesis null hypothesis even though it is false.
Now, we are given the null and alternative hypothesis as;
Null Hypothesis: μ ≤ 67.16
Alternative Hypothesis: μ > 67.16.
Where μ represents the statewide average bill.
We are also given the true statewide average bill is $51.28.
Now, the true statewide average bill falls within the range of the null hypothesis given.
Thus, we can't reject the null hypothesis since it is true.
Now, we are told the null hypothesis is not rejected and that is correct.
Thus, there is no error as it doesn't fall into the type I or the type II error.
Mr. Evans is currently 4 times as old as his son, Dan. If Mr. Evans was 46 years old 2 years ago, how old is Dan now?
Answers
Answer:
the son age is 13band Evans age is 52 years old at present day
Dan is 12 years old.
What is Algebra?A branch of mathematics known as algebra deals with symbols and the mathematical operations performed on them.
Variables are the name given to these symbols because they lack set values.
In order to determine the values, these symbols are also subjected to various addition, subtraction, multiplication, and division arithmetic operations.
Given:
let the Age of Dan is x years
Mr. Evans Age = 4x
If Mr. Evans was 46 years old 2 years ago
The, Present age of Mr. Evans = 48 years
So, Dan's Age = 48/4
= 12 years.
Hence, Dan is 12 years old.
Learn more about Algebra here:
https://brainly.com/question/24875240
#SPJ2
Scott needs to mail a gift card to a friend. He uses
47
-cent stamps and
7
-cent stamps to pay $2.91
$
2.91
in postage. How many of each stamp did Scott use?
Answers
Answer:
He used 5 47 cent stamps and 8 7 cent stamps
subtract 0.47 from 2.91 until you get 0.56 then you begin to subtract 0.07 to get 0.
8 of the 7 cent
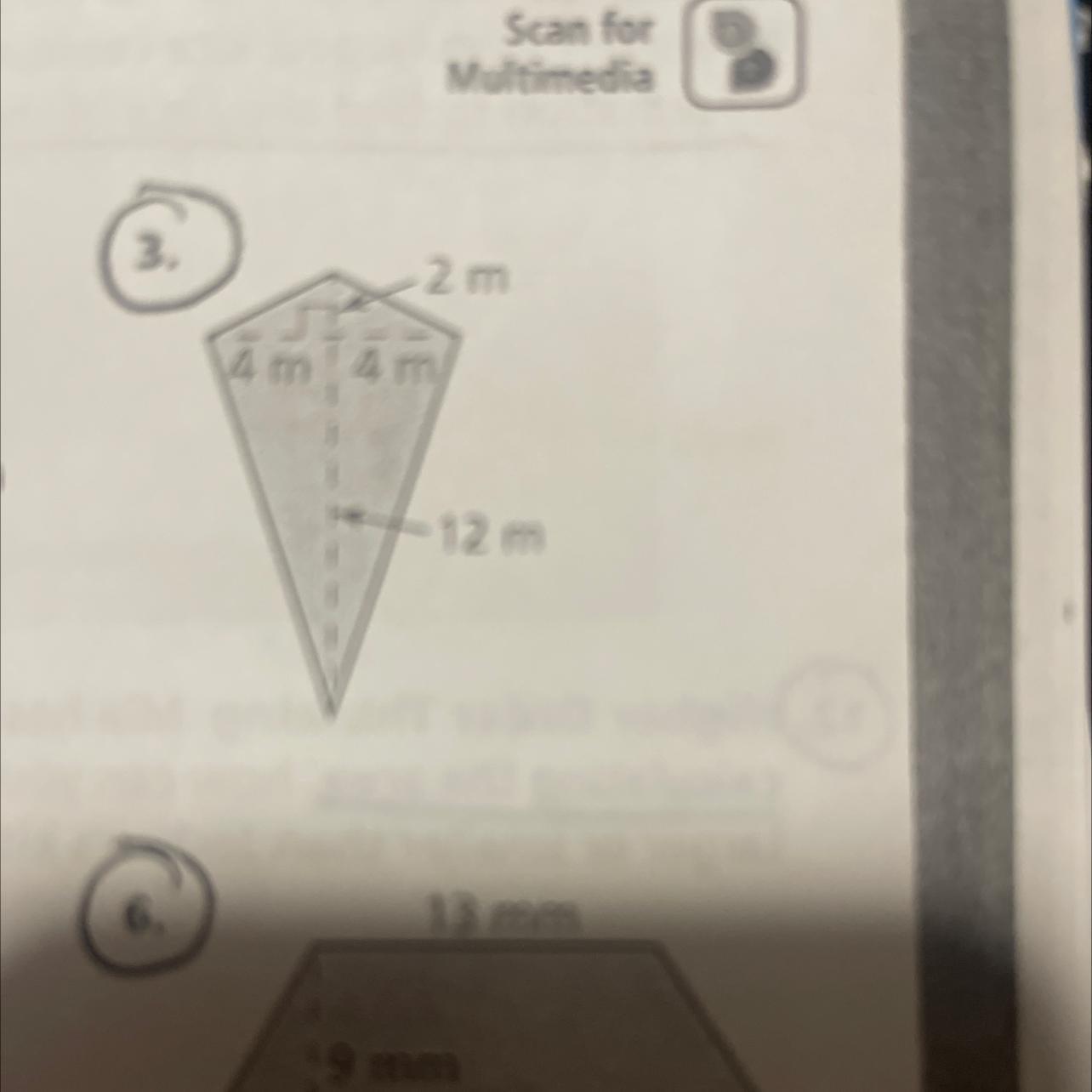
FIND THE AREA PLEASE
Answers
Answer:
the area of the shape is 48m
Step-by-step explanation:
10*4=40
2*4=8
40+8=48
brake it up into two triangles. one is a triangle that is 10m tall and 8m wide at the top. you can solve that by doing 4*10=40. the other triangle is 4m wide at the bottom and 2m tall. you can solve that by doing 2*4=8. and 40+8=48.
I WILL GIVE BRAINLIEST!
-2x + 8 = 2x + 10
COMBINE LIKE TERMS
Answers
Answer:
x= -1/2
Step-by-step explanation:
BECAUSE IT JUST DOES!!!!
Help me anyone I need it now!
Giving brainliest

Answers
Step-by-step explanation:
simple interest formula is I = p × r × t / 100
$32 = p × 8 × 3 / 100
$32 = 24p / 100
32 × 100 = 24p
3200 / 24 = $133.33
.) 1 remote controlled cars cost $27. Fill in the blanks
of the table.
Answers
Answer:
1:27
2:54
3:81
4:108
5:135
Step-by-step explanation:
If this answer helped you then please consider liking this and marking it as brainliest :)
4 2/3 - 5/6= / \ 2/6 3/6
Answers
You have the following expression:
4 2/6 - 5/6
consider that 5/6 = 2/6 + 3/6, then:
4 2/6 - 5/6 = 4 2/6 - (2/6 + 3/6) = 4 2/6 - 2/6 - 3/6 = 4 3/6 = 4 1/2
Hence, the result is 4 1/2
Percent of change
Find the Percent of decrease for the following problems:
1. Chad played three hours of Pokémon Go per day during the summer. Since
school began, he is only allowed to play one hour per day.
2. Karen has 7 Eevees in her Pokémon stash. She transferred some in to the
Professor and now only has 2 Eevees.
3. It takes 200 coins to get a bag upgrade in Pokémon Go. The creators
decided to throw a sale on bag upgrades. For one day only, anybody can
upgrade their bag for 125 coins.
Answers
Answer:
1. 33%
2. 28
3. 62.5
Step-by-step explanation:
10.64 - 8.5=
before you can subtract these two decimals what do you do
Answers
nothing u can add a zero after the five but it won’t do anything
How to prove this differential with limit?
\( \frac{d {e}^{ \\ x} }{dx} = {e}^{x} \)
Answers
The differentiation of \(e\x^{x}\) is \(e\x^{x}\) proved using the first law of differentiation or limit law.
What is Differentiation ?A technique for determining a function's derivative is differentiation. Mathematicians use a procedure called differentiation to determine a function's instantaneous rate of change based on one of its variables. The most typical illustration is velocity, which is the rate at which a distance changes in relation to time.
Differentiation is the ratio of a slight change in one quantity to a little change in another that depends on the first quantity. Calculus' major emphasis on the differentiation of a function makes it one of the subject's key ideas. Differentiation is the process of determining the maximum or lowest value of a function, the speed and acceleration of moving objects, and the tangent of a curve. If y = f(x) and f(x) is differentiable, then f'(x) or dy/dx is used to indicate the differentiation.
\(\frac{d}{dx}e\x^{x}\) using first order or limits to differentiate we get
for \(\lim_{h \to0} \frac{f(x+h) - f(x)}{h} = \frac{d}{dx}f(x)\)
therefore,
\(\lim_{h \to 0} \frac{e\x^{(x +h)}- e\x^{x} }{h} \\\) = \(\lim_{h \to 0} \frac{e\x^{x}(e\x^{h}-1 ) }{h}\) = \(\lim_{h \to 0} \frac{e\x^{x}*e\x^{h} }{1} \\\) ( using L-Hospital)
\(\lim_{h \to 0} e\x^{x} * e\x^{h} = e\x^{x} (proved)\)
To learn more about Differentiation refer to :
https://brainly.com/question/28974113
#SPJ1
by what number should 2/9 be divided to obtain 8/3
Answers
Answer:
\( \frac{1}{12} \)
Step-by-step explanation:
\( \frac{2}{9} \div \frac{8}{3} \\ = \: \frac{1}{12}\)
So, if you divide 2/9 by 1/12, you'll get 8/3
Answered by GAUTHMATH
Mr. Walker asked his students to use the associative property to find an expression that is equivalent to (13 + 15 + 20) + (20 + 47 + 18). The expressions that four students created are shown in the table below.
Expressions Generated by Students
Student
Expression
Jeremy
(20 + 13 + 15) + (20 + 47 + 18)
Layla
(20 + 47 + 18) + (13 + 15 + 20)
Keith
(13 + 20) + (20 + 47 + 18) + 15
Melinda
(13 + 15 + 20 + 20) + (47 + 18)
How many of the students correctly applied only the associative property to rewrite the expression?
one
two
three
four
