Brian flips a fair coin 3 times. What is the probability of getting 3 heads?
Answers
If Brain flips a coin 3 times the probability of getting 3 heads is 0.125.
The given statement is Brian flips a fair coin 3 times.
We need to find the probability of getting 3 heads.
What is probability?Probability refers to possibility. A random event's occurrence is the subject of this field of mathematics. The range of the value is 0 to 1.
The possible outcomes are {HHH, THH, HTH, HHT, TTH, THT, HTT, TTT}.
Total number of outcomes = 8
The number of favourable outcomes =1
So, the probability of getting 3 heads = 1/8 = 0.125
Hence, if Brain flips a coin 3 times the probability of getting 3 heads is 0.125.
To learn more about the probability visit:
https://brainly.com/question/11034287.
#SPJ1
Related Questions
Lenny earned $1,200 over the summer working at the waterpark . He deposited half of the money in an account that earns 2% interest compounded monthly He deposited the other half of the money in an account that earns 4 % interest compounded continuously . Assuming there are no other deposits or withdrawals find the difference in the interest earned his two investments after 10 years.
Answers
After 10 years, there is a difference of approximately $165.15 in interest earned between Lenny's two investments.
Lenny earned $1,200 during the summer and decided to deposit half in two different accounts. The first account has a 2% interest rate compounded monthly, while the second account has a 4% interest rate compounded continuously. To determine the difference in interest earned in these two investments after 10 years, we must first calculate the final balance for each account and then find the difference.
For the first account, he deposited $600. With a 2% annual interest rate compounded monthly, the formula to calculate the final balance is:
A1 = P(1 + r/n)^(nt)
where A1 is the final balance, P is the initial deposit, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years.
A1 = 600(1 + 0.02/12)^(12*10)
A1 ≈ $732.81
For the second account, he also deposited $600. With a 4% annual interest rate compounded continuously, the formula is:
A2 = Pe^(rt)
where A2 is the final balance, P is the initial deposit, e is the base of the natural logarithm, r is the annual interest rate, and t is the number of years.
A2 = 600 * e^(0.04*10)
A2 ≈ $897.96
Now, we can find the difference in interest earned:
Difference = (A2 - P) - (A1 - P)
Difference = ($897.96 - $600) - ($732.81 - $600)
Difference ≈ $165.15
To learn more about annual interest rate : brainly.com/question/20631001
#SPJ11
You are flipping two coins. Find the probability of flipping two tails.
A. 1/2
B. 1/24
C. 1/8
D. 1/4
Answers
Answer:
D. 1/4
Step-by-step explanation:
The probability of flipping a tail is 1/2. To find the probability of flipping two tails, multiply.
1/2 x 1/2 = 1/4
Answer: Here we will learn how to find the probability of tossing two coins.
Let us take the experiment of tossing two coins simultaneously:
When we toss two coins simultaneously then the possible of outcomes are: (two heads) or (one head and one tail) or (two tails) i.e., in short (H, H) or (H, T) or (T, T) respectively; where H is denoted for head and T is denoted for tail.
Therefore, total numbers of outcome are 22 = 4
The above explanation will help us to solve the problems on finding the probability of tossing two coins.
Step-by-step explanation:
THE ANSWER MUST BE AT LEAST 1/4 OR 1/8
IF THAT IS WRONG LET ME KNOW!
AND IF YOU NEED A TUTOR I AM OPEN FOR HELP JUST CONTACT ME IF YOU HAVE ANY QUESTIONS!
(Laws of Exponents with Whole Number Exponents MC)
Evaluate one third raised to the seventh power divided by one third raised to the sixth power comma all raised to the second power.
one eighteenth
one ninth
1
one and one ninth
Answers
The simplified form of the given expression is 1/9. Therefore, option B is the correct answer.
The given expression is \((\frac{(\frac{1}{3})^{7}}{(\frac{1}{3})^{6} } )^{2}\).
We need to evaluate the given expression.
What are the laws of exponents?Laws of exponents:
When multiplying like bases, keep the base the same and add the exponents. When raising a base with power to another power, keep the base the same and multiply the exponents. When dividing like bases, keep the base the same and subtract the denominator exponent from the numerator exponent.Now, \((\frac{(\frac{1}{3})^{7}}{(\frac{1}{3})^{6} } )^{2}=((\frac{1}{3})^{7-6})^{2}\) (Because \(\frac{a^{m} }{a^{n} } =a^{m-n}\))
\(=(\frac{1}{3})^{2}\)
=1/9
The simplified form of the given expression is 1/9. Therefore, option B is the correct answer.
To learn more about the laws of exponents visit:
https://brainly.com/question/568161.
#SPJ1
Hi ! It would be awesome If some genius could check if I’m right plis :^

Answers
Answer:
D. 12 units
Step-by-step explanation:
For a point to be translated x units to the left, we must subtract x from the original point, so the x coordinate for M' is -4 as 4 - 8 = -4
For a point to be translated x units down, we must subtract x from the original point, so the y coordinate for M' is -3 as 6 - 9 = -3
Thus, the coordinates for M' is (-4, -3)
The formula for distance, d, between two points is
\(d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2 }\), where (x1, y1) is one point and (x2, y2) is another point.
If we allow M (4, 6) to be our x1 and y1 point and M' (-4, -3) to be our x2 and y2 point, we can find the distance between the two points:
\(d=\sqrt{(4-(-4))^2+(6-(-3))^2}\\ d=\sqrt{(4+4)^2+(6+3)^2}\\ d=\sqrt{(8)^2+(9)^2}\\ d=\sqrt{64+81}\\ d=\sqrt{145}\\ d=12.04159458\)
Please answer quick ill give brainliest to the best
Jerome parked his car for 4½ hours each day for two days at two different parking lots. The cost of parking at each parking lot is shown below. Day 1 - $5.00 for the first hour plus $1.50 for every additional hour. Day 2 - $2.50 for the first hour plus $1.50 for every additional hour. How much more money did Jerome pay on Day 1 compared to Day 2?
A) $19.00
B)$3.50
C) $18.00
D) $2.50
Answers
hope this helped you out!!
Jerome spent $80 on a meal and he left a 15% tip. How much was the
tip that Jerome left?
Answers
Answer:
12
Step-by-step explanation:
If you multiply .15 times 80, you get 12. therefore the tip was 12 dollars
Given the system of linear equations:
2 – 2y = 4
4x + 3y = 5
What would be a possible FIRST STEP in the process of SOLVING by ELIMINATION?
Answers
you could multiple the first equation by 3 and the second equation by 2 so you can eliminate the y variable
hope this helps
c) 2 x x 3 x y
Please help
Answers
PLS HELP I WAS SUPPOSE TO SO THIS TODAY BUT I FELL ASLEEP AND IN HAVING TROUBLE

Answers
What is the perimeter of this trapezoid?

Answers
I really need some help on this math problem please

Answers
Answer:
16.8 cubic centimeters
Step-by-step explanation:
3 cm * 4 cm * 1.4 cm = the volume of the prism
3 * 4 = 12
12 * 1.4
1 + 0.4 = 1.4
12 * 1 = 12
12 * 0.4 = 4.8
12 + 4.8 = 16.8
the volume of the prism is 16.8 cubic centimeters
Can someone help me with this, and if you can Explain it.

Answers
Answer:
20
Step-by-step explanation:
Since C is the midpoint of BD, BC must be equal to CD. Therefore, we can set the equation:
x+4=3x-10
Solve:
14=2x
x=7
Then we find AC, which is:
2x-5+x+4 = 3x-1
We can plug x in to get:
3*(7)-1=20
Use the information given below to find tan(a+b).
12
COS = with a in quadrant I
13
3
tanſ = with ß in quadrant III
4'
Give the exact answer, not a decimal approximation.

Answers
what is 3/4 of 2483???
Answers
Answer:
1862.25
Step-by-step explanation:
.......
help!!! please see attached

Answers
The speed of the runner at a time of 2 hours is approximately 11 kilometers per hour.
How to estimate the speed of a runner by trangent line
In this question we find a smooth curve for runner's distance, in kilometers, in time, in hours, and the speed at t = 2 hours can be estimated by constructing a line tangent to the curve. The speed (v), in kilometers per hour, can be estimated by secant line formula:
v ≈ [x(3 h) - x(1 h)] / (3 h - 1 h)
Where:
x(1) - Distance at t = 1, in kilometers.x(3) - Distance at t = 3, in kilometers.If we know that x(1 h) = 22 km and x(3 h) = 44 km, then the velocity of the runner is:
v ≈ (44 km - 22 km) / (3 h - 1 h)
v ≈ 22 km / 2 h
v ≈ 11 km / h
To learn more on tangent lines: https://brainly.com/question/28994498
#SPJ1
Match the missing parts of the triangle with their correct length or measure.
HINT: The ONLY right triangles we are given in this problem are ADB and BDC. Triangle ABC is NOT necessarily a right triangle.
Given:
DB=24
AD=32
AC=42
DC=10
BC=26
AB=40
Measure
Measure of
Find:
Measure
Measure
Measure
Measure
Measure

Answers
The length of DB, AD and AC are 24 m, 32 m, 42 m respectively. The measurement of ∠C = 67.38°.
What is a right angle triangle?
A right triangle, also known as a right-angled triangle, right-perpendicular triangle, orthogonal triangle, or formerly rectangled triangle, is a triangle with one right angle, or two perpendicular sides. The foundation of trigonometry is the relationship between the sides and various angles of the right triangle.
Given that, in △BCD
BD = 24 m
DC = 10 m
BC = 26 m
△BCD is a right angle triangle.
The trigonometry ratio of sine is ratio of height to hypothenuse.
With respect to C, the height of △BCD is 24m and hypothenuse is 26m.
sin C = height/hypothenuse
sin C = 24/26
C = 67.38°
To learn more about measurement of an angle of right angle triangle, click on below link:
https://brainly.com/question/9281904
#SPJ1
students deliver newspapers and magazines to houses.
one day,they have to deliver 875 newspapers and 1200 magazines.
each student can deliver 35 newspapers or 50 magazines in 1 hour.
each student can only work for 8 hours
work out the minimum number of students needed
Answers
Answer:
4 students for newspapers & 3 students for magazines are needed for the deliveries to be made in a day.
Step-by-step explanation:
According to the question,
875 newspapers & 1200 magazines are to be delivered in a day by students.In an hour each student can deliver 35 newspapers or 50 magazines & each student can only work for 8 hoursSo, In 8 hours each student can deliver:
35 × 8 = 280 newspapers
50 × 8 = 400 magazines
To find out minimum number of students needed to work we need to divide work done by each student in 8 hours by total deliveries to be made.
\( \therefore\)
For Newspapers:
875/280 = 3.125
So, by rounding of the figure we will need 4 students to deliver newspapers as each student can work only for 8 hours.
For magazines:
1200/400 = 3
3 students are needed to deliver magazines.
Helppp pleaseeeeeeeeeeeeeeee…………

Answers
The expression that represents the number of football cards that Frankie has is given as follows:
F = J + 65.
How to model the situation?The situation can be modeled by a system of equations, in which the variables are given as follows:
Variable F: number of football cards that Frankie has.Variable J: number of football cards that John has.Frankie has sixty-five more football cards than his friend John, hence the expression that represents the number of football cards that Frankie has is given as follows:
F = J + 65.
As the term sixty-five more means that the number 65 is added to the amount of cards that John has, which is symbolized by J, to obtain the amount F, which is the number of football cards that Frankie has.
Missing InformationThe problem asks for the expression of the number of cards that Frankie has.
More can be learned about a system of equations at https://brainly.com/question/24342899
#SPJ1
The state of a spin 1/2 particle in Sx basis is defined as (Ψ) = c+l + x) + i/√7 l - x) a) Find the amplitude c+ assuming that it is a real number and the state vector is properly defined. b) Find the expectation value . c) Find the uncertainty △SX.
Answers
1) The amplitude c+ is c+l
2) The expectation value is 0
3) The uncertainty ΔSX is √(3/7) c+.
Now, we know that any wave function can be written as a linear combination of two spin states (up and down), which can be written as:
Ψ = c+ |+> + c- |->
where c+ and c- are complex constants, and |+> and |-> are the two orthogonal spin states such that Sx|+> = +1/2|+> and Sx|-> = -1/2|->.
Hence, we can write the given wave function as:Ψ = c+|+> + i/√7|->
Now, we know that the given wave function has been defined in Sx basis, and not in the basis of |+> and |->.
Therefore, we need to write |+> and |-> in terms of |l> and |r> (where |l> and |r> are two orthogonal spin states such that Sy|l> = i/2|l> and Sy|r> = -i/2|r>).
Now, |+> can be written as:|+> = 1/√2(|l> + |r>)
Similarly, |-> can be written as:|-> = 1/√2(|l> - |r>)
Therefore, the given wave function can be written as:Ψ = (c+/√2)(|l> + |r>) + i/(√7√2)(|l> - |r>)
Therefore, we can write:c+|l> + i/(√7)|r> = (c+/√2)|+> + i/(√7√2)|->
Comparing the coefficients of |+> and |-> on both sides of the above equation, we get:
c+/√2 = c+l/√2 + i/(√7√2)
Therefore, c+ = c+l
The amplitude c+ is a real number and is equal to c+l
The expectation value of the operator Sx is given by: = <Ψ|Sx|Ψ>
Now, Sx|l> = 1/2|r> and Sx|r> = -1/2|l>
Hence, = (c+l*) + (c+l) + (i/√7) - (i/√7)(c+l*)= -i/√7(c+l*) + i/√7(c+l)= 2i/√7 Im(c+)
As c+ is a real number, Im(c+) = 0
Therefore, = 0
The uncertainty ΔSX in the state |Ψ> is given by:
ΔSX = √( - 2)
where = <Ψ|Sx2|Ψ>and2 = (<Ψ|Sx|Ψ>)2
Now, Sx2|l> = 1/4|l> and Sx2|r> = 1/4|r>
Hence, = (c+l*) + (c+l) + (i/√7) - (i/√7)(c+l*)= 1/4(c+l* + c+l) + 1/4(c+l + c+l*) + i/(2√7)(c+l* - c+l) - i/(2√7)(c+l - c+l*)= = 1/4(c+l + c+l*)
Now,2 = (2i/√7)2= 4/7ΔSX = √( - 2)= √(1/4(c+l + c+l*) - 4/7)= √(3/14(c+l + c+l*))= √(3/14 * 2c+)= √(3/7) c+
Learn more about the wave function at
https://brainly.com/question/31744195
#SPJ11
a smallercircle passes through the center of, and is tanget to a larger cirlc the area of the smaller circle is 9 square units. What is teh area of the larger circle in square units
Answers
36 square units make up the larger circle's surface area.
We can use the fact that the smaller circle is tangent to the larger circle and passes through its center to find the area of the larger circle. Since the radius of the smaller circle is tangent to the larger circle, the radius of the larger circle is double the radius of the smaller circle.
Let's call the radius of the smaller circle "r" and the radius of the larger circle "R". We know that R = 2r.
We know that the area of a circle is given by the formula A = πr^2.
We know that the area of the smaller circle is 9 square units, we can use this formula to find the radius:
A = πr^2 => r^2 = 9/π => r = sqrt(9/π)
Now we can use the formula of the area of a circle with R-value to get the area of the larger circle:
A = πR^2 => A = π(2r)^2 => A = 4πr^2 => A = 4π(9/π) => A = 36
So the area of the larger circle is 36 square units
To learn more about the area of the circle, refer to the link:brainly.com/question/28642423
#SPJ4
$64 for four video games
What is the ratio and unit rate
Answers
Answer:
16 for each video game
Step-by-step explanation:
The unit rate is 16x
the ratio is 16:1
The slope is y=16x
Answer:
The ratio: $65:4
The unit rate: 16.25:1
Step-by-step explanation:
The ratio is money to video games.
The unit rate is how much money each video games cost.
help quickly pls area of a triangle: sine formula

Answers
Answer:
If you were to use the sine formula you would have to use the cosine formula to get one of the opposite sides and then use the sine formula.
For the area why not use 1/2 * 20 to get the base.
Then the height would be 24 * sin 63 = 21.38
That would give an area of 213.8
Solve the equation: 12 - x (x - 3) = (6 - x)(x + 2)
Answers
Answer: the answer is 0
Why 0?:
Step 1: Simplify both sides of the equation
-x * x= -x²
-x * -3= 3x all together it is ( -x²+3x+12)
for the other side:
-x * x= -x²
6 * x= 6x and x * 2= 2x and 6 * 2= 12
then subtract 6x-4x= 2x so final would be = −x²+4x+12
Step 2: Add x² to both sides.
−x²+3x+12+x²=−x²+4x+12+x² then we are left with 3x+12=4x+12
Step 3: Subtract 4x from both sides.
3x+12−4x=4x+12−4x --> −x+12=12
Step 4: Subtract 12 from both sides.
−x+12−12=12−12
−x=0
Step 5: Divide both sides by -1 or -x
x=0
what is the volume of the cone?
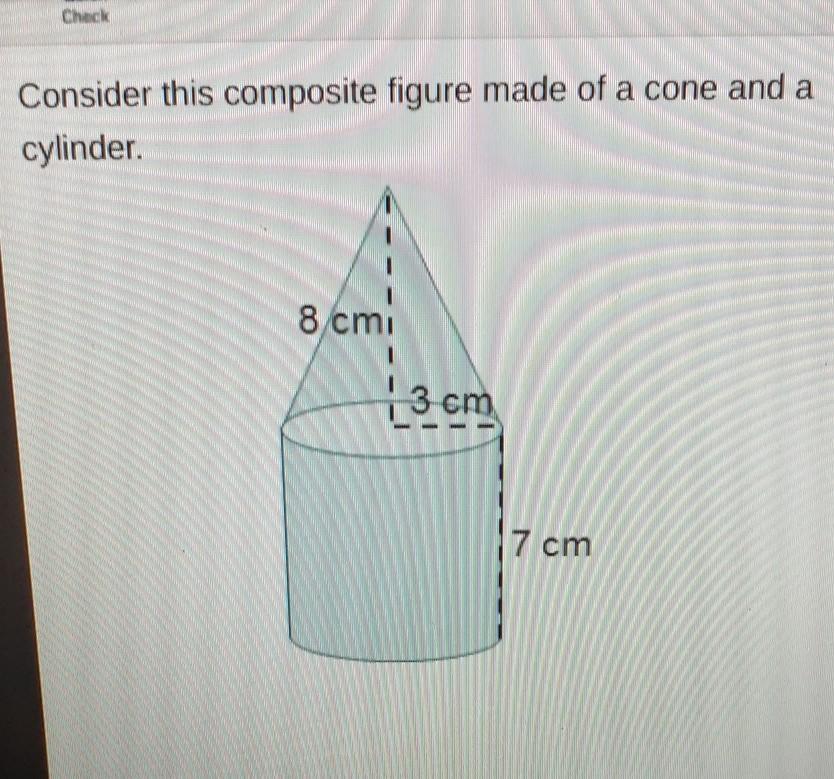
Answers
Answer:
The volume of the cone is 75.36 cm³
Step-by-step explanation:
The rule of the volume of a cone is V = \(\frac{1}{3}\) π r² h, where
r is the length of the radius of its baseh is the height of the coneIn the given figure
∵ The length of the radius of the cone is 3 cm
∴ r = 3 cm
∵ The length of the height of the cone is 8 cm
∴ h = 8 cm
→ Substitute the values of r and h in the rule of the volume above
∵ π ≅ 3.14
∵ V = \(\frac{1}{3}\) (3.14)(3)²(8)
∴ V = 75.36 cm³
∴ The volume of the cone is 75.36 cm³
Suppose that X is a random variable with mean 20 and standard deviation 4. Also suppose that Y is a random variable with mean 40 and standard deviation 7. Find the mean and the variance of the random variable Z for each of the following cases. Be sure to show your work.
(a) Z = 40 - 5X
(b) Z = 15X - 20
(c) Z = X + Y
(d) Z = X - Y
(e) Z = -2X + 3Y
Answers
(a) The mean of Z in case (a) is -60 and the variance is 400.
(b) The mean of Z in case (b) is 280 and the variance is 3600.
(c) The mean of Z in case (c) is 60 and the variance is 65.
(d) The mean of Z in case (d) is -20 and the variance is 65.
(e) The mean of Z in case (e) is 80 and the variance is 505.
To find the mean and variance of the random variable Z for each case, we can use the properties of means and variances.
(a) Z = 40 - 5X
Mean of Z:
E(Z) = E(40 - 5X) = 40 - 5E(X) = 40 - 5 * 20 = 40 - 100 = -60
Variance of Z:
Var(Z) = Var(40 - 5X) = Var(-5X) = (-5)² * Var(X) = 25 * Var(X) = 25 * (4)² = 25 * 16 = 400
Therefore, the mean of Z in case (a) is -60 and the variance is 400.
(b) Z = 15X - 20
Mean of Z:
E(Z) = E(15X - 20) = 15E(X) - 20 = 15 * 20 - 20 = 300 - 20 = 280
Variance of Z:
Var(Z) = Var(15X - 20) = Var(15X) = (15)² * Var(X) = 225 * Var(X) = 225 * (4)² = 225 * 16 = 3600
Therefore, the mean of Z in case (b) is 280 and the variance is 3600.
(c) Z = X + Y
Mean of Z:
E(Z) = E(X + Y) = E(X) + E(Y) = 20 + 40 = 60
Variance of Z:
Var(Z) = Var(X + Y) = Var(X) + Var(Y) = (4)² + (7)² = 16 + 49 = 65
Therefore, the mean of Z in case (c) is 60 and the variance is 65.
(d) Z = X - Y
Mean of Z:
E(Z) = E(X - Y) = E(X) - E(Y) = 20 - 40 = -20
Variance of Z:
Var(Z) = Var(X - Y) = Var(X) + Var(Y) = (4)² + (7)² = 16 + 49 = 65
Therefore, the mean of Z in case (d) is -20 and the variance is 65.
(e) Z = -2X + 3Y
Mean of Z:
E(Z) = E(-2X + 3Y) = -2E(X) + 3E(Y) = -2 * 20 + 3 * 40 = -40 + 120 = 80
Variance of Z:
Var(Z) = Var(-2X + 3Y) = (-2)² * Var(X) + (3)² * Var(Y) = 4 * 16 + 9 * 49 = 64 + 441 = 505
Therefore, the mean of Z in case (e) is 80 and the variance is 505.
Learn more about Mean and Variance at
brainly.com/question/29253308
#SPJ4
find the nth term of a sequence whose first several terms are given. 2, 4, 8, 16,
Answers
Therefore, the nth term of the sequence is 2^(n-1).
To find the nth term of a sequence, we need to identify the pattern or rule that governs the relationship between the terms.
Looking at the given sequence, we can observe that each term is obtained by multiplying the previous term by 2.
Starting with the first term:
2 * 2 = 4
4 * 2 = 8
8 * 2 = 16
We can see that each term is double the value of the previous term.
Therefore, the rule for this sequence is that each term is obtained by multiplying the previous term by 2.
To find the nth term, we can express it as a formula:
aₙ = aₙ₋₁ * 2
where aₙ represents the nth term and aₙ₋₁ represents the (n-1)th term.
For this sequence, the first term is a₁ = 2.
Using the formula, we can find the nth term:
aₙ = a₁ * 2^(n-1)
Substituting the given first term, we have:
aₙ = 2 * 2^(n-1)
To know more about sequence,
https://brainly.com/question/1315120
#SPJ11
A family is having a pool built in their backyard. If their yard is rectangular and measures 10x by 10x and the pool is circular with a radius of 2x how much of the yard will be left over after the pool is built
Answers
Answer:
\(100x^2-4\pi x^2\)
Also can be said as:
\(4x^2(25-\pi )\)
Step-by-step explanation:
The scenario:The question is asking you, "how much is left over."
In this scenario, you're going to have to subtract the area of the pool (P) from the total area of the backyard (B), which will leave you with the remaining area of the backyard (x).
This means your equation to solve this question is:
\(x=B-P\)
Step 1:The value of B is the area of the backyard.
We are told that the backyard is a rectangular shape. So, we can use the formula of finding the area of a rectangle.
The formula is \(B=L*W\), where L is the length and W is the width.
Both the length and width are 10x, so we must plug that into this equation.
We end up getting:
\(B=10x*10x\)
Which can be simplified to:
\(B=100x^2\)
Step 2:The value of P is the area of the pool.
The pool is a circular shape. So, to get the area of it, we must use the formula of finding the area of a circle.
The formula is \(P=\pi r^2\), where r is the radius.
Plugging in the radius of 2x, we get:
\(P=\pi (2x)^2\)
By solving this out, we end up with:
\(P=4\pi x^2\)
Step 3:From the scenario, we have the equation:
\(x=B-P\)
And from steps 1 and 2, we have the values:
\(B=100x^2\) and \(P=4\pi x^2\)
Now we just plug those values in to get:
\(x=100x^2-4\pi x^2\)
And finally, the amount of the backyard remaining is:
\(100x^2-4\pi x^2\)
Different format:This answer may be simplified to:
\(4x^2(25-\pi )\)
what is the slope of the line that contains points (−3 −5) and (2 7)
Answers
Answer:
Step-by-step explanation:
To find the slope of a line when only given two points on that line, divide the difference in the y points by the difference in the x points.
slope = (-5 - 7)/(-3 - 2) = -12/-5 = 12/5
slope = (7 - -5)/(2 - -3) = 12/
Brian runs 7 miles in 50 minutes. At the same rate, how many miles would he run in 75 minutes?
Answers
Answer:
7/50 = x/75
x = 10.5
therefore he would run 10.5 miles in 75 minutes
Answer:
In 75 minutes, she runs (7/50) x 75 = 10.5.
She runs 10.5 miles in 75 minutes.
Step-by-step explanation:
how many different digits are used in the hexadecimal number system?
Answers
Answer:16
Step-by-step explanation: