Calculate each value requested for the following scores: 16, 23, 8, 25, 11, 20, and 10 a. sigma x b. [sigma x]^2 c. sigma x^2 d. n sigma x^2
Answers
The value requested for the following scores, which are 16, 23, 8, 25, 11, 20, and 10, are: a. sigma x = 113b. [sigma x]^2 = 12769 c. sigma x^2 = 3849 d. n sigma x^2 = 26943
Given scores are: 16, 23, 8, 25, 11, 20, and 10.σx = Σx/n
where Σx = sum of all values of x, and n = total number of values of xσx
= (16+23+8+25+11+20+10)/7σx
= 113/7σx
= 16.14σx^2
= Σx²/n where Σx² = sum of the square of all values of x, and n = total number of values of xσx^2
= (16² + 23² + 8² + 25² + 11² + 20² + 10²)/7σx^2
= 3849/7σx^2 = 549.857[σx]²
= (Σx)²/n where Σx = sum of all values of x, and n = total number of values of x[σx]²
= (16+23+8+25+11+20+10)²/7[σx]²
= 16129/7[σx]²
= 2304.14nσx²
= n(Σx²) where Σx² = sum of the square of all values of x, and n = total number of values of xnσx²
= 7(16² + 23² + 8² + 25² + 11² + 20² + 10²)nσx²
= 7(3849)nσx²
= 26943
Therefore, the value requested for the following scores are: a. σx = 113 b. [σx]² = 12769 c. σx² = 3849 d. nσx² = 26943
To know more about scores, click on the link below:
https://brainly.com/question/12905637#
#SPJ11
Related Questions
The sum of the reciprocals of two consecutive odd integers is 12/35. Find the two integers.
Answers
The two consecutive odd integers are 9 and 11. 1/8 plus 1/11 equals 12/35.
The sum of the reciprocals of two consecutive odd integers is 12/35.
1/x + 1/(x+2) = 12/35
(x+2)/(x*35) + (x/35) = 12/35
x + 2 + x = 12
2x = 10
x = 5
5 and 7 are the next two odd numbers.
The sum of the reciprocals of two consecutive odd integers is 12/35. To find the two integers, we need to solve for x. Since the two integers are consecutive and odd, the equation
1/x + 1/(x+2) = 12/35
can be used to find x. We can then multiply both sides of the equation by x*35 and simplify it to (x+2)/(x*35) + (x/35) = 12/35.
By subtracting x/35 from both sides and then adding 2 to both sides, we can get the equation
x + 2 + x = 12.
By solving the equation 2x = 10, we find that x = 5. This means that the two consecutive odd integers are 5 and 7. This can also be verified by checking that 1/5 + 1/7 is equal to 12/35.
Learn more about integer here
https://brainly.com/question/15276410
#SPJ4
SHOW WORK PLEASE Find the future value of an annuity of $500 per year for 12 years if the interest rate is 5%.
Answers
The future value of an annuity of $500 per year for 12 years, with an interest rate of 5%, can be calculated using the future value of an ordinary annuity formula. The future value is approximately $7,005.53.
To calculate the future value of an annuity, we can use the formula:
FV = P * [(1 + r)^n - 1] / r
Where:
FV is the future value of the annuity,
P is the annual payment,
r is the interest rate per compounding period,
n is the number of compounding periods.
In this case, the annual payment is $500, the interest rate is 5% (or 0.05), and the number of years is 12. As the interest is compounded annually, the number of compounding periods is the same as the number of years.
Plugging the values into the formula:
FV = $500 * [(1 + 0.05)^12 - 1] / 0.05
= $500 * [1.05^12 - 1] / 0.05
≈ $500 * (1.795856 - 1) / 0.05
≈ $500 * 0.795856 / 0.05
≈ $399.928 / 0.05
≈ $7,998.56 / 100
≈ $7,005.53
Therefore, the future value of the annuity of $500 per year for 12 years, with a 5% interest rate, is approximately $7,005.53.
Learn more about here:
#SPJ11
Help meeeeeeeeeeeeee

Answers
The distance between point P and line l is
1. Distance = 2√2
2. Distance =0
3. Distance =6
4. Distance =1
5. Distance =√10
To find the distance between a point and a line, we can use the formula for the distance between a point and a line in the coordinate plane. The formula is:
Distance = |Ax + By + C| / √(A² + B²)
1. Line & contains points (0, -3) and (7, 4). Point P has coordinates (4,3).
The equation of the line is y = x - 3. We can rewrite it as x - y + 3 = 0.
So, Distance = |4 - 3 + 3| / √(1² + (-1)²)
= |4| / √2
= 4 / √2
= 2√2
2. Line & contains points (11, -1) and (-3, -11). Point P has coordinates (-1, 1).
The equation of the line is y = -2x - 1. We can rewrite it as 2x + y + 1 = 0.
So, Distance = |2(-1) + 1 + 1| / √(2² + 1²)
= |-2 + 2| / √5
= 0 / √5
= 0
3. Line & contains points (-2, 1) and (4, 1). Point P has coordinates (5, 7).
The equation of the line is y = 1.
So, Distance = |0(5) + 7 - 1| / √(0² + 1²)
= |6| / √1
= 6
4. Line & contains points (4, -1) and (4, 9). Point P has coordinates (1, 6).
The line is vertical, and its equation is x = 4.
so, Distance = |1 - 4 + 4| / √(1² + 0²)
= |-1| / √1
= 1
5. Line & contains points (1, 5) and (4, -4). Point P has coordinates (-1, 1).
The equation of the line is y = -3x + 8.
So, Distance = |3(-1) + 1 - 8| / √(3² + 1²)
= |-3 - 7| / √10
= |-10| / √10
= 10 / √10
= 10√10 / 10
= √10
Learn more about Distance formula here:
https://brainly.com/question/25841655
#SPJ1
what do we call premises or starting points that are based on scientific testing, methodical experimentation, or measurable, validated, and verified evidence?
Answers
Answer:
empirical and topical
Step-by-step explanation:
starting points (empirical, topical) common grounds you locate between yourself and your composite audience that will allow you to build conviction toward your conclusion. Empirical Starting points: Dealing in certainty, concrete evidence.
Does anyone know the answer to this?
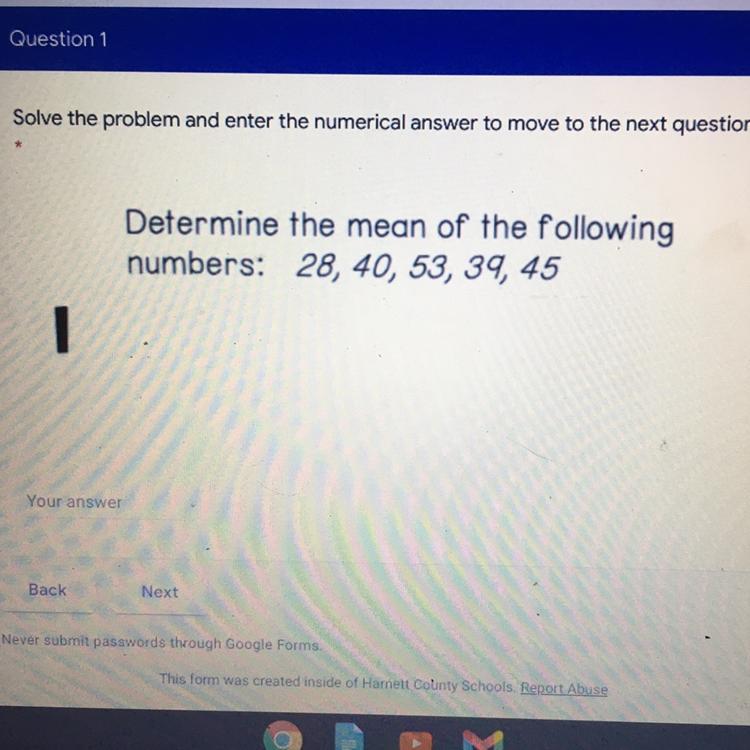
Answers
Answer:
41
Step-by-step explanation:
pizza HELP me this is really important answer for both questions
3. In a given city, the number of rainy days and the number of sunny days are recorded.
A. If 15% of days are sunny and the rest are rainy, what is the ratio of sunny days to rainy days? B. If 50% of days are sunny and 50% of days are rainy, what is the ratio of sunny days to rainy days?
Answers
Answer:
i think the ratio for the first is 1:5 and the other is 1:1
Step-by-step explanation:
have a nice day
Find the equation of a line parallel to 3x + 3y = 21 that passes through the point
(8,-2).
Answers
Answer:
do you have like any picture of a graph?
During a routine check of the fluoride content of Gotham City's water supply, the given results were obtained from replicate analyses of a single sample: 0.815mg/L,0.789mg/L,0.811mg/L,0.789mg/L, and 0.815mg/L. Determine the mean and 90% confidence interval for the average fluoride concentration in this sample. Report the mean and the confidence interval using the "real rules" for significant figures.
Answers
To determine the mean and 90% confidence interval for the average fluoride concentration in the sample, we can follow these steps: The correct answer is 90% confidence interval = 0.791 to 0.817 mg/L
The first step is to calculate the mean of the data:
mean = (0.815 + 0.789 + 0.811 + 0.789 + 0.815) / 5 = 0.804 mg/L
The next step is to calculate the standard deviation of the data:
std_dev = sqrt((\(0.009^{2}\) + \(0.015^{2}\) + \(0.002^{2}\) + \(0.015^{2}\) + \(0.009^{2}\)) / 5) = 0.008 mg/L
The 90% confidence interval for the mean is calculated using the following formula:
mean ± t * std_dev / sqrt(n)
where t is the 90% critical value for the t-distribution with 4 degrees of freedom, which is 1.685.
90% confidence interval = 0.804 ± 1.685 * 0.008 / \(\sqrt{5}\) = 0.791 to 0.817 mg/L
The mean fluoride concentration in the sample is 0.804 mg/L. The 90% confidence interval for the mean is 0.791 to 0.817 mg/L.
Reporting:
The mean and the confidence interval should be reported to 3 significant figures, since the original data was given to 3 significant figures.
mean = 0.804 mg/L
90% confidence interval = 0.791 to 0.817 mg/L
Learn more about mean here:
brainly.com/question/26509052
#SPJ11
Evaluate f(x)=4x+5 when x=4.
Answers
21
Step-by-step explanation:
=4x+5
=4*4+5
=16+5
=21
The value of function f(x) = 4x + 5 when x = 4 is 21 the answer is 21.
What is a function?It is defined as a special type of relationship, and they have a predefined domain and range according to the function every value in the domain is related to exactly one value in the range.
We have a function:
f(x) = 4x + 5
Plug x = 4
f(4) = 4(4) + 5
f(4) = 16 + 5
f(4) = 21
Thus, the value of function f(x) = 4x + 5 when x = 4 is 21 the answer is 21.
Learn more about the function here:
brainly.com/question/5245372
#SPJ2
Can y’all help me on question 14?!

Answers
Answer:
The answer is 3.2
Step-by-step explanation:
A house that was originally listed for sale at $450,000 has decreased the asking price by 8%. By how much has the price been reduced?
Answers
= 36,000
They reduce $36,000 from the original price.
Construct a 90% confidence interval for the population mean you. Assume the population has a normal distribution a sample of 15 randomly selected math majors had mean grade point average 2.86 with a standard deviation of 0.78
Answers
The 90% confidence interval is: (2.51, 3.22)
Confidence interval :It is a boundary of values which is eventually to comprise a population value with a certain degree of confidence. It is usually shown as a percentage whereby a population means lies within the upper and lower limit of the provided confidence interval.
We have the following information :
Number of students randomly selected, n = 15.Sample mean, x(bar) = 2.86Sample standard deviation, s = 0.78Degree of confidence, c = 90% or 0.90The level of significance is calculated as:
\(\alpha =1-c\\\\\alpha =1-0.90\\\\\alpha =0.10\)
The degrees of freedom for the case is:
df = n - 1
df = 15 - 1
df = 14
The 90% confidence interval is calculated as:
=x(bar) ±\(t_\frac{\alpha }{2}\), df \(\frac{s}{\sqrt{n} }\)
= 2.86 ±\(t_\frac{0.10 }{2}\), 14 \(\frac{0.78}{\sqrt{15} }\)
= 2.86 ± 1.761 × \(\frac{0.78}{\sqrt{15} }\)
= 2.86 ± 0.3547
= (2.51, 3.22)
Learn more about Confidence interval at:
https://brainly.com/question/32546207
#SPJ4
Mr. Zuro finds the mean height of all students in his statistics class to be inches. Just as mr. Zuro finishes explaining how to get the mean, danielle walks in late. Danielle is inches tall. What is the mean height of the students in the class?.
Answers
Mean height of the students in the class = 65.7 inches
The mean height of all 12 students in the class is 66.0 inches.
So the Total height of 12 students in the class = 66 × 12
= 792 inches
As Danielle's height = 62.1 inches
So the total height of 13 students = 792 + 62.1
= 854.1 inches
Mean of all 13 students in the class = 854.1 / 13
= 65.7 inches
To know more about the Average refer to the link given below:
https://brainly.com/question/20118982
#SPJ4
The complete question:
Mr. Zuro finds the mean height of all 12 students in his class to be 66.0 inches. Just as Mr. Zuro finishes explaining how to get the mean, Danielle walks in late. Danielle is 62.1 inches tall. What is the mean of the 13 students in the class?
1.5 grams of potassium 40 is found in a material. We know that it orginally contained 6 grams. How many half lives have passed since this material formed
Answers
Approximately 2 half-lives have passed since the material containing potassium-40 (K-40) was formed.
Here we know that,
Initial mass of potassium-40 (K-40) = 6 grams
Current mass of potassium-40 (K-40) = 1.5 grams
The relationship between the number of half-lives and the remaining amount of a radioactive substance can be expressed using the formula:
Remaining amount = Initial amount × (1/2)^(number of half-lives)
Let's solve the equation for the number of half-lives. We can rearrange the formula to solve for the number of half-lives as follows:
(number of half-lives) = log(base 1/2) (remaining amount / initial amount)
Substituting the given values:
(number of half-lives) = log(base 1/2) (1.5 grams / 6 grams)
Using the logarithmic properties, we can rewrite the equation as:
(number of half-lives) = log(base 1/2) (1.5) - log(base 1/2) (6)
To simplify further, we can use the change of base formula to convert the logarithm to a base 10 logarithm:
(number of half-lives) = log(1.5) / log(1/2) - log(6) / log(1/2)
Evaluating the logarithms:
(number of half-lives) = 0.1761 / (-0.3010) - 0.7782 / (-0.3010)
(number of half-lives) = -0.5847 - (-2.5814)
(number of half-lives) = -0.5847 + 2.5814
(number of half-lives) = 1.9967
Since the number of half-lives must be a whole number, we can conclude that approximately 2 half-lives have passed since the material containing potassium-40 (K-40) was formed.
To know more about half life here
https://brainly.com/question/31666695
#SPJ4
The monthly payments on a five-year loan at 7.5% compounded monthly are $200.38. 0. What was the original amount of the loan? (Do not round intermediate calculotions and round your final answer to 2 decimal ploces.) Amount $ b. What is the balance after the 30
th
payment? (Do not round intermediote calculotions and round your finol answer to 2 decimal places.) Balance $
Answers
The original amount of the loan is approximately $6,605.45, and the balance after the 30th payment can be calculated using the remaining number of payments, interest rate, and the original loan amount
The original amount of the loan can be calculated using the monthly payment amount and the interest rate. The balance after the 30th payment can be determined by considering the remaining number of payments and the interest accrued on the loan.
To find the original amount of the loan, we need to calculate the present value (PV) using the monthly payment amount, interest rate, and the loan term. In this case, the loan term is five years, or 60 months, and the monthly payment is $200.38.
Using the formula for the present value of an ordinary annuity:
PV = PMT × [(1 - (1 + r)^(-n)) / r]
Where PMT is the monthly payment, r is the monthly interest rate, and n is the number of periods (number of months in this case).
First, we need to convert the annual interest rate to a monthly interest rate. The annual interest rate is 7.5%, so the monthly interest rate is 7.5% / 12 = 0.075 / 12 = 0.00625.
Next, we can substitute the values into the formula to find the present value (original amount of the loan):
PV = $200.38 × [(1 - (1 + 0.00625)^(-60)) / 0.00625]
≈ $200.38 × 32.9536
≈ $6,605.45
Therefore, the original amount of the loan is approximately $6,605.45.
To find the balance after the 30th payment, we need to consider the remaining number of payments and the interest accrued on the loan. Since each monthly payment reduces the loan balance, we need to calculate the remaining loan balance after 30 payments.
Using the formula for the remaining balance of a loan:
Balance = PV × (1 + r)^n - PMT × [(1 + r)^n - 1] / r
Where PV is the present value (original loan amount), r is the monthly interest rate, n is the remaining number of periods (remaining number of months), and PMT is the monthly payment.
Substituting the values into the formula:
Balance = $6,605.45 × (1 + 0.00625)^(60 - 30) - $200.38 × [(1 + 0.00625)^(60 - 30) - 1] / 0.00625
Calculating the expression will give the balance after the 30th payment.
learn more about balance here
https://brainly.com/question/27154367
#SPJ11
Write an equation in point-slope form for the line with a slope of 1/4 that passes through the point (-1, -8)
Answers
Answer:
y = 1/4 x - 31/4
Step-by-step explanation:
Slope (m) = 1/4
Point A (-1, -8)
y = mx + b
-8 = 1/4 (-1) + b
-8 + 1/4 = b
b = -32/4 + 1/4
b = -31/4
y = mx + b <-- this is a linear equation, continuing line, so there are infinite values for x and y. Therefore we don't have to plug the values of x and y in
y = 1/4 x + - 31/4
y = 1/4 x - 31/4
what is the higher (stronger) correlation? write the letter of the correct answer. a. 0.87 b. -0.89 c. -0.2 d. 1.2
Answers
The strongest correlation is - 0.89 that is option B
To gauge how closely two variables are related to one another, correlation coefficients are used. The most common correlation coefficient is Pearson's, though there are other varieties as well. The correlation coefficient known as Pearson's is frequently applied in linear regression. Correlation coefficients typically fall between -1.00 and +1.00. The strongest correlation is taken into account when the value is closest to +1 or -1, according to the rule of correlation coefficients.
A positive correlation coefficient means that the two variables directly affect one other's values. There is no association between the two variables, according to a zero correlation coefficient and when the correlation coefficient is negative, it means that the values of the two variables are inversely related.
To learn more about correlation, visit: https://brainly.com/question/28898177
#SPJ4
Find the nonpermissible replacement for y inthis expression.(y +3)/(y-1)
Answers
To find the nonpermissible replacement for y in the expression;
\(\frac{y+3}{y-1}\)The nonpermissible replacement for y is the replacement for y at which the denominator of the expression is zero. (when the denomenator is zero, the final value can not be determined).
For the given expression, the denomenator is;
\(y-1\)For y to be nonpermissible, the denometor must be equal to zero.
\(y-1=0\)To get y, add 1 to both sides.
\(\begin{gathered} y-1+1=0+1 \\ y=1 \end{gathered}\)At y =1, the expression becomes;
\(\frac{y+3}{y-1}=\frac{1+3}{1-1}=\frac{4}{0}\rightarrow\text{ nonpermissible }\)Therefore, the nonpermissible replacement for y in the given expression is;
\(y=1\)Graph h(x) = 38(0.51)x. What is the constant percent rate of change of f(x) with respect to x? Does the graph show growth or decay?
49% growth
49% decay
51% growth
51% decay
Answers
Answer:
Step-by-step explanation:
This is decay, the rate of change is 49%
hope this helps!
The correct rate of change is B)49% decay.
What constant rate of change ?
A rate of change is constant when, at any given point along the function, the ratio of the output to the input remains constant. The slope is another name for the rate of change that is constant. A linear function's rate of change will be constant.
Here the given function is ,
=> h(x)=38(0.51)x.
For any exponential function in which the base is less than 1, it will be an exponential decay situation.
In this problem, the base is 0.51.
Then,The amount that the base is less than 1 ( i.e. 1 - base) . It represents the rate of change in decimal ,
=> 1-0.51 = 0.49
Converting into percentage => 0.49 *100 = 49%
Therefore the correct option is B) 49% decay.
To learn more about rate of change in function
https://brainly.com/question/23299538
#SPJ1
find the derivative of the function g(x) = (x^2 - x +
1)^10.(tanx)^3.
Answers
The derivative of the function g(x) = (x² - x + 1\()^1^0\) * (tan(x))³ is g'(x) = 10(x² - x + 1)⁹ * (2x - 1) * (tan(x))³ + 3(x² - x + 1\()^1^0\) * (tan(x))² * sec²(x).
To find the derivative of the given function g(x), we can apply the product rule and the chain rule. Let's break down the function into its constituent parts: f(x) = (x² - x + 1\()^1^0\) and h(x) = (tan(x))³.
Using the product rule, the derivative of g(x) can be calculated as g'(x) = f'(x) * h(x) + f(x) * h'(x).
First, let's find f'(x). We have f(x) = (x² - x + 1\()^1^0\), which is a composite function. Applying the chain rule, f'(x) = 10(x² - x + 1\()^9\) * (2x - 1).
Next, let's determine h'(x). We have h(x) = (tan(x))³. Applying the chain rule, h'(x) = 3(tan(x))² * sec²(x).
Now, we substitute these derivatives back into the product rule formula:
g'(x) = f'(x) * h(x) + f(x) * h'(x)
= 10(x² - x + 1)² * (2x - 1) * (tan(x))³ + 3(x² - x + 1\()^1^0\)* (tan(x))² * sec²(x).
In summary, the derivative of the function g(x) = (x² - x + 1\()^1^0\) * (tan(x))³ is g'(x) = 10(x² - x + 1)⁹ * (2x - 1) * (tan(x))³ + 3(x² - x + 1\()^1^0\) * (tan(x))² * sec²(x).
Learn more about derivative
brainly.com/question/29144258
#SPJ11:
For what values of a make each expression true. |a|=-a
Answers
Answer:
a=0
Step-by-step explanation:
Pls help math algebra Match the algebraic expressions and the algebraic equations

Answers
2x^2-3x+1 - Algebraic Expression
x^3-2x^2=x Algebraic Equation
x^2-5x+6=0 Algebraic Equation
5x+20 Algebraic Expression
y=-2x+3 Algebraic Equation
-x-5 Algebraic Expression
Hope it helps you! :)
\(********************************************\)
Please mark Brainliest if this answer is helpful!
- Your friend, \(GraceRosalia\)
*Just a teen who listens to music
Answer:
1. Expression
2. Equation
3. Equation
4. Expression
5. Equation
6. Expression
Step-by-step explanation:
Algebraic Equation is basically algebraic expression except there's one difference.
Algebraic Equation must always have = sign.
The = sign applies to all equations, no matter what equation it is.
Next is Algebraic Expression;
Algebraic Expression does not have =, <, ≠, >, ≤ and ≥.
To put it simply, algebraic expression is just terms there; no comparison between two.
Usually, algebraic expression refers to polynomial, square root, etc.
So now, you understand the difference between two?
Algebraic Equation has =Algebraic Expression does not have any comparisons (>, = as examples)1. 2x^2-3x+1 is algebraic expression because there is no comparison.
2. x^3-2x^2=x is algebraic equation because there is comparison between two expressions.
3. x^2-5x+6=0 is algebraic equation because there is comparison between one expression and a constant.
4. 5x+20 is algebraic expression because there is no comparison.
5. y = -2x+3 is algebraic equation because there is comparison between x-term and y-term.
6. -x-5 is algebraic expression because no comparison.
find the matrix a' for t relative to the basis b'. t: r2 → r2, t(x, y) = (−8x y, 8x − y), b' = {(1, −1), (−1, 5)}
Answers
The matrix of \(t\) relative to the basis \(b'\) is \(A' = \begin{bmatrix} -9 & 7 \\ -37 & 43 \end{bmatrix}\).
\(\textbf{To find the matrix of } t \textbf{ relative to the basis } b', \textbf{we have to follow some steps. The steps are described below:}\)
First, we have to find the images of basis vectors under the transformation \(t\). \(t(-1,1) = (-9,7)\) and \(t(1,-5) = (-37,43)\).
Represent the image vectors of the basis in the standard basis. We use these vectors as columns in the matrix of \(t\) in the basis \(b'\).
\((-9,7) = -9(1,0) + 7(0,1) = (-9,7) = -9(-1,1) + 7(1,-5)\)
\((-37,43) = -37(1,0) + 43(0,1) = (-37,43) = -37(-1,1) + 43(1,-5)\)
Hence, we can write the following equation: \(A[x]_{b'} = [x]_S\)
Where \(A[x]_{b'}\) is the main answer in the form of a matrix, and \([x]_S\) is the coordinate of \([x]_{b'}\) with respect to the standard basis.
Now, we will write the equations with the coordinates of the basis vectors of \(b'\).
\(A[1,0] = [-9, -37]\) and \(A[0,1] = [7, 43]\)
Now we will write the matrix of \(A\) as follows:
\(A = \begin{bmatrix} -9 & 7 \\ -37 & 43 \end{bmatrix}\)
Thus, the matrix of \(t\) relative to the basis \(b'\) is \(A' = \begin{bmatrix} -9 & 7 \\ -37 & 43 \end{bmatrix}\).
To know more about matrix, click here
https://brainly.com/question/29132693
#SPJ11
dellana company tested 50 products for 75 hours each. during this time, it experienced four breakdowns. compute the number of failures per hour. what is the mean time between failures?
Answers
dellana company tested 50 products for 75 hours each. during this time, it experienced four breakdowns. compute the number of failures per hour, 937.50 hours is the mean time between failures.
What is mean time?The span of time before something occurs or before a given time frame expires. We can utilise the current computers while waiting for the new ones to arrive next week.
Given that,
dellana company tested 50 products
time =75 hours
Thus, total products in hours
= 50 products × 75 hours each
= 3750 product hours
Also said that, 4 breakdowns in 3750 product hours,
so, (4/3750) = 1.067 × 10⁻³ = 0.001067 breakdowns per hour.
Also, an average of 0.001067 breakdowns per hour = λ
therefore, mean time between failures:
= 1/ λ
= 1/0.001067
= 937.50 hours
To know more about mean time refer to:
https://brainly.com/question/28840486
#SPJ4
it is assumed that approximately 15% of adults in the u.s. are left-handed. consider the probability that among 100 adults selected in the u.s., there are at least 30 who are left-handed. given that the adults surveyed were selected without replacement, can the probability be found by using the binomial probability formula with x counting the number who are left-handed? why or why not?
Answers
Option C. No, because the 100 adults were selected without replacement, the selections are dependent.
The binomial probability formula assumes that the trials are independent, meaning that the probability of success or failure for each trial remains the same regardless of the outcomes of previous trials. However, in this case, the 100 adults were selected without replacement, so the probability of being left-handed for each selection depends on the outcomes of previous selections. Therefore, the binomial probability formula cannot be used to find the probability in this situation. Instead, the hypergeometric distribution can be used to account for the dependence between selections.
Learn more about probability here: brainly.com/question/30034780
#SPJ4
Complete question:
It is assumed that approximately 15% of adults in the U.S. are left-handed. Consider the probability that among 100 adults selected in the U.S., there are at least 30 who are left-handed. Given that the adults surveyed were selected without replacement, can the probability be found by using the binomial probability formula with x counting the number who are left-handed? Why or why not?
A. Yes, because the 100 adults represent less than 5% of the U.S. adult population, the trials can be treated as independent.
B. No, because the 30 adults represent more than 5% of the sample size, the trials are dependent.
C. No, because the 100 adults were selected without replacement, the selections are dependent.
D. No, because the probability of being right-handed is greater, x must count the number of right-handed adults.
A 6ft tall construction worker is standing at the tip of the Burj Khalifa’s shadow. His job is to attach a cable from the tip of the building to where he stands. He notices his shadow is 3ft and the Burj Khalifa is 2720ft tall. How long will the cable need to be?
Please someone help this is due Thursday
Answers
The length of the cable needed is 1360ft.
To find the length of the cable needed for the construction worker to attach from the tip of the Burj Khalifa to where he stands, we can use the concept of similar triangles.
Let's represent the length of the cable as "x."
According to the given information, the height of the construction worker is 6ft, and the length of his shadow is 3ft. Similarly, the height of the Burj Khalifa is 2720ft, and the length of its shadow is the unknown variable "x."
We can set up the following proportion based on the similar triangles formed by the construction worker and the Burj Khalifa:
(Length of construction worker's shadow) / (Height of construction worker) = (Length of Burj Khalifa's shadow) / (Height of Burj Khalifa)
Using the values given:
3ft / 6ft = x / 2720ft
Now, we can solve this proportion for "x":
(3/6) * 2720 = x
Simplifying:
(1/2) * 2720 = x
1360 = x
Therefore, the length of the cable needed is 1360ft.
To know more about length of the cable here
https://brainly.com/question/30932684
#SPJ4
A construction worker, standing at the tip of the Burj Khalifa’s shadow, must attach a cable from the tip of the building to where he stands. The worker notices that his shadow is 3ft and the Burj Khalifa is 2720ft tall.
In the given question, the worker notices that his shadow is 3ft and the Burj Khalifa is 2720ft tall.
Therefore, the height of the construction worker can be found using the concept of similar triangles, which states that corresponding angles in similar triangles are equal.
Hence, height of the worker can be calculated as (height of the Burj Khalifa / length of its shadow) x length of worker’s shadow = (2720 / 3) x 6
= 2720 x 2
= 5440 feet.
Thus, the length of the cable needed will be the sum of the height of the Burj Khalifa and the height of the construction worker,
which is 2720 + 5440 = 8160 feet.
Learn more about Burj Khalifa from the given link:
https://brainly.com/question/30637543
#SPJ11
let sugar be the explanatory variable and calories be the response variable; which scenario best describes ŷ
Answers
The amount of calories in fruit juice increases by 2.5 for every one gram of sugar. The calorie amount estimated by this model is 57 if there are zero grams of sugar.
Quantity of sugar=x ( in grams)
The juice's calorie count=y
Estimate of y, which means it's the juice's estimated calorie count=ŷ
Rearranging the regression equation, we get: ŷ=57+2.5x
This has the mathematical formula y = mx+c, where m is the slope and c is the y-intercept.
Here m= 2.5 and c=57
We can get the rate of change from the slope. It specifically informs us of the increase in calories (y) that occurs every time sugar (x) increases. Whenever x increases by 1, y increases by 2.5.
The starting or initial number of calories is represented by the y-intercept 57. You begin with 57 calories if you have 0 grams of sugar, the least amount of sugar that is feasible. Plugging x = 0 into = 2.5x + 57 (you should get = 57) will show us this. Where the line crosses the y-axis can be seen as the y-intercept.
Therefore, The amount of calories in fruit juice increases by 2.5 for every one gram of sugar. The calorie amount estimated by this model is 57 if there are zero grams of sugar
Learn more about calories here:
https://brainly.com/question/10075900
#SPJ4
The coordinates of point T are (0,5). The midpoint of ST is (5,-8). Find the coordinates of point S.
The other endpoint is
(Type an ordered pair.)
... HELP PLS!!!!
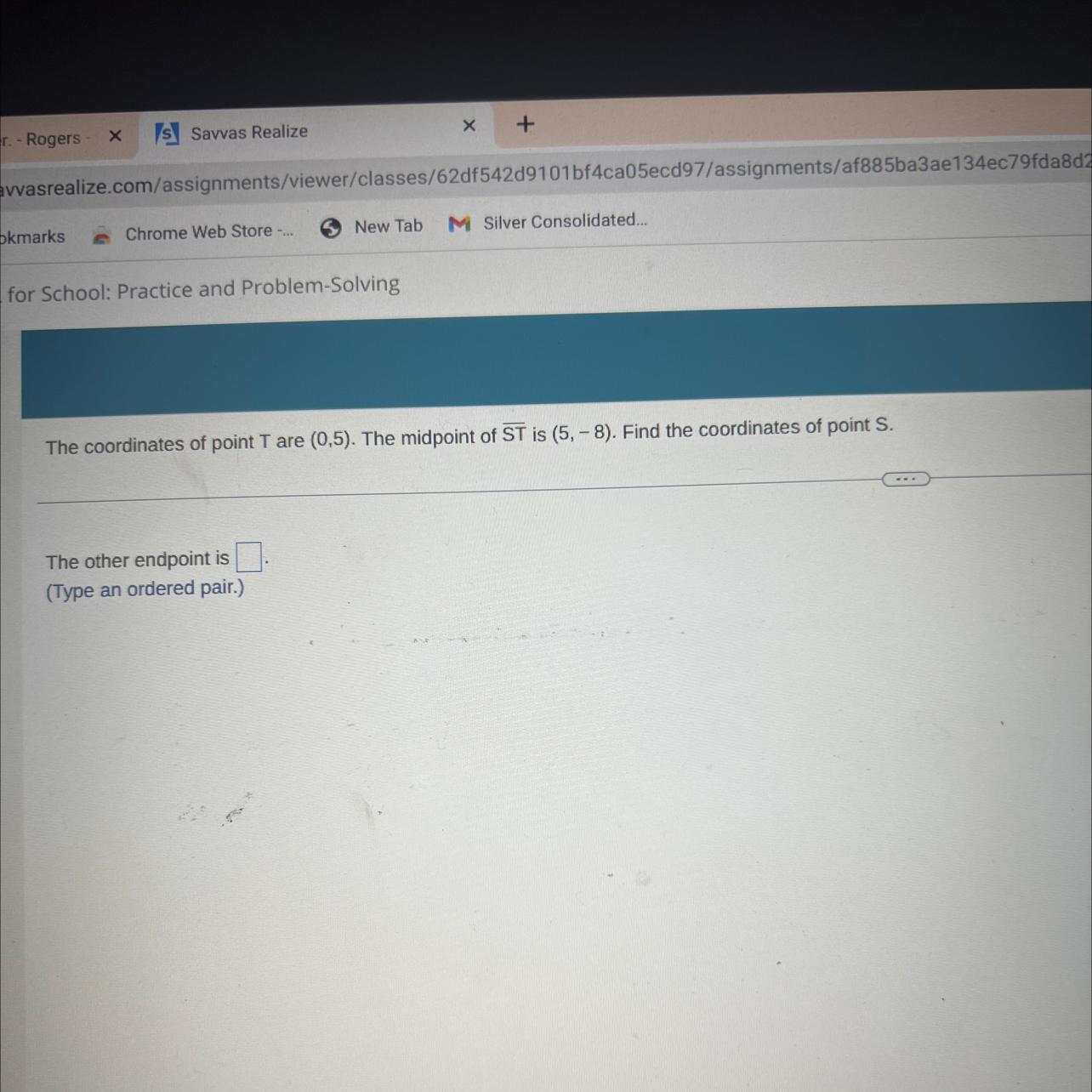
Answers
I hope this helps
consider the following line integral. xy dx x2 dy, c is counterclockwise around the rectangle with vertices (0, 0), (5, 0), (5, 1), (0, 1)
Answers
The line integral of xy dx + x^2 dy around the given rectangle is 0.
To evaluate the line integral ∮C (xy dx + x^2 dy) along the given rectangle C with vertices (0, 0), (5, 0), (5, 1), and (0, 1), we can break it down into four line integrals along each side of the rectangle and sum them up.
Along the bottom side:
Parametrize the line segment from (0, 0) to (5, 0) as r(t) = (t, 0), where t ranges from 0 to 5. The differential element along this line segment is dr = (dt, 0). Substituting these values into the line integral, we get:
∫[0,5] (t*0) dt = 0.
Along the right side:
Parametrize the line segment from (5, 0) to (5, 1) as r(t) = (5, t), where t ranges from 0 to 1. The differential element along this line segment is dr = (0, dt). Substituting these values into the line integral, we get:
∫[0,1] (5t0 + 25dt) = ∫[0,1] 25*dt = 25.
Along the top side:
Parametrize the line segment from (5, 1) to (0, 1) as r(t) = (5-t, 1), where t ranges from 0 to 5. The differential element along this line segment is dr = (-dt, 0). Substituting these values into the line integral, we get:
∫[0,5] ((5-t)*0 + (5-t)^2 * 0) dt = 0.
Along the left side:
Parametrize the line segment from (0, 1) to (0, 0) as r(t) = (0, 1-t), where t ranges from 0 to 1. The differential element along this line segment is dr = (0, -dt). Substituting these values into the line integral, we get:
∫[0,1] (0*(1-t) + 0) dt = 0.
Summing up all the line integrals, we have:
0 + 25 + 0 + 0 = 25.
Therefore, the line integral of xy dx + x^2 dy around the given rectangle is 25.
For more questions like Line integral click the link below:
https://brainly.com/question/32517303
#SPJ11
Lisa is checking out at the bookstore. Each book (b) costs $1.50 and she has a $5 off coupon she can use. She wants to spend $25 or less in the bookstore. How many books can Lisa buy?
Answers
Answer:
20
Step-by-step explanation:
Given:
Lisa is checking out at the bookstore.
Each book (b) costs $1.50 and she has a $5 off coupon she can use.
She wants to spend $25 or less in the bookstore.
Solve:
Since there is a $5 off coupon..
$1.5b - $5.00<=$25.00
$1.5b<= $30.00
$1.5b/1.5 = $30.00/1.5
b=20
Lisa can buy 20 book.
~lenvy~