Caleb is a fashion designer. He designed a jacket with 2 types of fabric. Now Caleb has to make samples. He buys 68 yards of nylon and 94 yards of wool. The nylon is $3 a yard, and a yard of wool is 3 times more expensive. How much did Caleb spend?
Answers
To find out how much the wool costs, we need to multiply the price of a yard of nylon by 3, since the wool is 3 times more expensive. So a yard of wool costs $3 * 3 = $<<3*3=9>>9.
To find out how many yards of wool Caleb bought, we need to divide the total number of yards by the number of fabrics, since he bought the same amount of each fabric. So Caleb bought 68 / 2 = <<68/2=34>>34 yards of wool.
To find out how much Caleb spent on wool, we need to multiply the number of yards of wool by the price of a yard of wool. So Caleb spent 34 * $9 = $<<34*9=306>>306 on wool.
To find out how much Caleb spent on nylon, we need to multiply the number of yards of nylon by the price of a yard of nylon. So Caleb spent 68 * $3 = $<<68*3=204>>204 on nylon.
To find out how much Caleb spent in total, we need to add the amount he spent on wool and the amount he spent on nylon. So Caleb spent $306 + $204 = $<<306+204=510>>510 in total. Answer: \boxed{510}.
Related Questions
is f(x)= 4x/5 +8/3 a linear function
Answers
Answer:
yes
Step-by-step explanation:
f(x) = 4x/5 + 8/3 can be written as
f(x) = 4/5 x + 8/3
which is in the form
y = mx + b
The form y = mx + b is the slope-intercept form of the equation of a line, so
f(x) = 4x/5 + 8/3 is a linear function.
Danielle was completing her science project and mixed saline solutions A and B. Brand A was a six gallon 18% saline solution and she ended up with an 18 gallon 8% saline solution mixture. Find the percent of saline solution in brand B.
A. 2.1%
B. 21%
C. 3%
Answers
Brand B contains 3% saline solution by volume. Then, C is the right answer.
Percentage of saline solution in brand B, let x be.
We know that the overall volume of saline solution in the combination is 18% of 6 gallons plus x% of (18 - 6) gallons since Danielle blended brands A and B to make a total of 18 gallons of 8% saline solution.
Then the equation is given as,
0.18(6) + 0.01x(18 - 6) = 0.08(18)
Simplifying and solving for x, we get:
1.08 + 0.12x = 1.44
0.12x = 0.36
x = 3
Therefore, the percentage of saline solution in brand B is 3%.
More about the percentage link is given below.
https://brainly.com/question/8011401
#SPJ1
What is the meaning of "the notion of finiteness"?

Answers
The notion of finiteness refers to the idea that something has a definite limit or is not infinite. It is a concept that has been applied in various fields of study, such as mathematics, computer science, and philosophy.
In mathematics, finiteness is a fundamental concept used to define various mathematical objects and structures, such as sets, numbers, and sequences. It is also used to define the properties of functions and to study the properties of mathematical systems.
In computer science, the notion of finiteness is crucial for the design and analysis of algorithms and computer programs. Computer scientists use finite state machines, which are mathematical models that describe the behavior of a system that can be in one of a finite number of states.
This concept is essential to the development of computer programs that are efficient, reliable, and secure.
In philosophy, finiteness is a concept that is often used to reflect on the nature of human existence and the limits of human knowledge. It is also used to examine the concept of time and the nature of reality.
In general, the notion of finiteness is a fundamental concept that has many applications in various fields of study.
To learn more about : finiteness
https://brainly.com/question/32403180
#SPJ8
NO LINKS!!!
answer all 3!!!!
easy brainliest!!



Answers
Answer:
Step-by-step explanation:
1) DE = 6/sin63 = 6.7
DF = 6/tan63 = 3.1
m∠E = 180 - 90 - 63 = 27°
2) tan30 = 1/√3 = UV / (27√10)
UV = (27√10) / √3 · (√3/√3) = (27√30) / 3 = 9√30
3) cosV = 3/8
cos⁻¹(3/8) = 68
m∠V = 68°
A chef used 0.65 cups of baking soda in a recipe. Which fraction is equivalent to this amount of baking soda in cups?
Answers
2. 65 and 100 both have a common factor of 5
3. You can simplify 65/100 to 13/20
Answer: 13/20
So the answer is 13/20
PLEASE HELP ASAP
Use the discriminant to determine how many real number solutions exist for the quadratic equation −4x2 + 3x –28 = 0.
Question 2 options:
A)
0
B)
3
C)
2
D)
1
Answers
A scientist has two solutions what she has labeled solution a and solution b each contains salt she knows that solution a is 60% salt and solution b is 85% salt she wants to obtain 70 ounces of a mixture that is 80% salt how many ounces of each solution should she use
Answers
Solving a system of equations we can see that:
She needs to use 56 oz of the 85% solution.She needs to use 14 oz of the 60% solution.How many ounces of each solution should she use?We can use the variables:
x = mass of the 60% solution.
y = mass of the 85% solution.
We can write a system of equations.
x + y = 70
x*0.6 + y*0.85 = 70*0.8
We can isolate x on the first equation to get:
x = 70 - y
Replace that in the other one:
(70 - y)*0.6 + y*0.85 = 70*0.8
Now we can solve this for y.
y*0.25 = 70*0.8 - 70*0.6
y = 14/0.25 = 56
Then he needs to use 56 ounces of the 85% solution, and 14 ounces of the 60% solution.
Learn more about systems of equations at:
https://brainly.com/question/13729904
#SPJ1
In Math town,60% of the population are males and 30% of them have brown eyes. Of the total math town population 28 % have brown eyes. What percentage of the females in math town have brown eyes?
Answers
25% percent of the females in Math town have brown eyes. To find the number of females with brown eyes, we need to subtract the number of males with brown eyes from the total number of people with brown eyes
what is percent ?
A percent is a way of expressing a number as a fraction of 100. The symbol for percent is %, which means "per hundred".
In the given question,
Let's assume that there are 100 people in Math town.
60% of them are males, so there are 60 males and 40 females.
Out of the 60 males, 30% have brown eyes, so there are 18 males with brown eyes.
28% of the entire population have brown eyes, so there are 28 people with brown eyes.
To find the number of females with brown eyes, we need to subtract the number of males with brown eyes from the total number of people with brown eyes:
28 - 18 = 10
So, there are 10 females with brown eyes.
Out of the 40 females in Math town, what percentage have brown eyes?
10 brown-eyed females out of 40 females is:
10/40 = 0.25 or 25%
Therefore, 25% of the females in Math town have brown eyes.
To know more about percent , visit:
https://brainly.com/question/28670903
#SPJ1
Please help me with this proof.

Answers
Answer:
See below
Step-by-step explanation:
For the second step, \(\angle T\cong\angle R\) by Alternate Interior Angles. The rest of the steps appear to be correct.
The values in the table represent a linear relationship between x and y.
x -8.5 -6.5 -2.5 -1
y -92 -72 -32 -17
What is the rate of change of y with respect to x?
Answers
The rate of change of y with respect to x for the given linear relationship is 10.
To determine the rate of change of y with respect to x, we can calculate the slope of the linear relationship between x and y using the formula:
slope = (change in y) / (change in x)
Given the values in the table:
x: -8.5, -6.5, -2.5, -1
y: -92, -72, -32, -17
We can calculate the change in y and change in x between any two points.
For example, between the first two points (-8.5, -92) and (-6.5, -72), the change in y is:
change in y = -72 - (-92) = -72 + 92 = 20
And the change in x is
change in x = -6.5 - (-8.5) = -6.5 + 8.5 = 2
Using the formula for slope:
slope = (change in y) / (change in x) = 20 / 2 = 10.
Therefore, the rate of change of y with respect to x is 10.
This means that for every unit increase in x, y increases by 10 units.
We can perform the same calculations for the other points in the table and observe that the rate of change of y with respect to x remains constant at 10.
Hence, the rate of change of y with respect to x for the given linear relationship is 10.
For similar question on linear relationship.
https://brainly.com/question/30300982
#SPJ11
PLEASE HELP...What is “b” ?

Answers
Solution,
B+22=180°
or,b=180-22
b=158°
Hope it helps
Good luck on your assignment
Answer:
158°
Step-by-step explanation:
b = 180-22= 158°{ angles in a straight line sum up to 180° meaning 22+b = 180°}
what is - 9 1/8 as a decimal number
Answers
Answer:
-9.125
Step-by-step explanation:
Answer:
It is -9.125.
Step-by-step explanation:
Please mark me Brainliest
Determine which answer in the solution set will make the equation true.
4p + 5 = 6p − 15
S: {−10, 0, 10, 20}
A: 0
B: −10
C: 20
D: 10
Answers
Answer:
d) 10
Step-by-step explanation:
Let's solve the problem,
→ 4p + 5 = 6p - 15
→ 6p - 4p = 5 + 15
→ 2p = 20
→ p = 20/2
→ [ p = 10 ]
Hence, option (d) is correct.
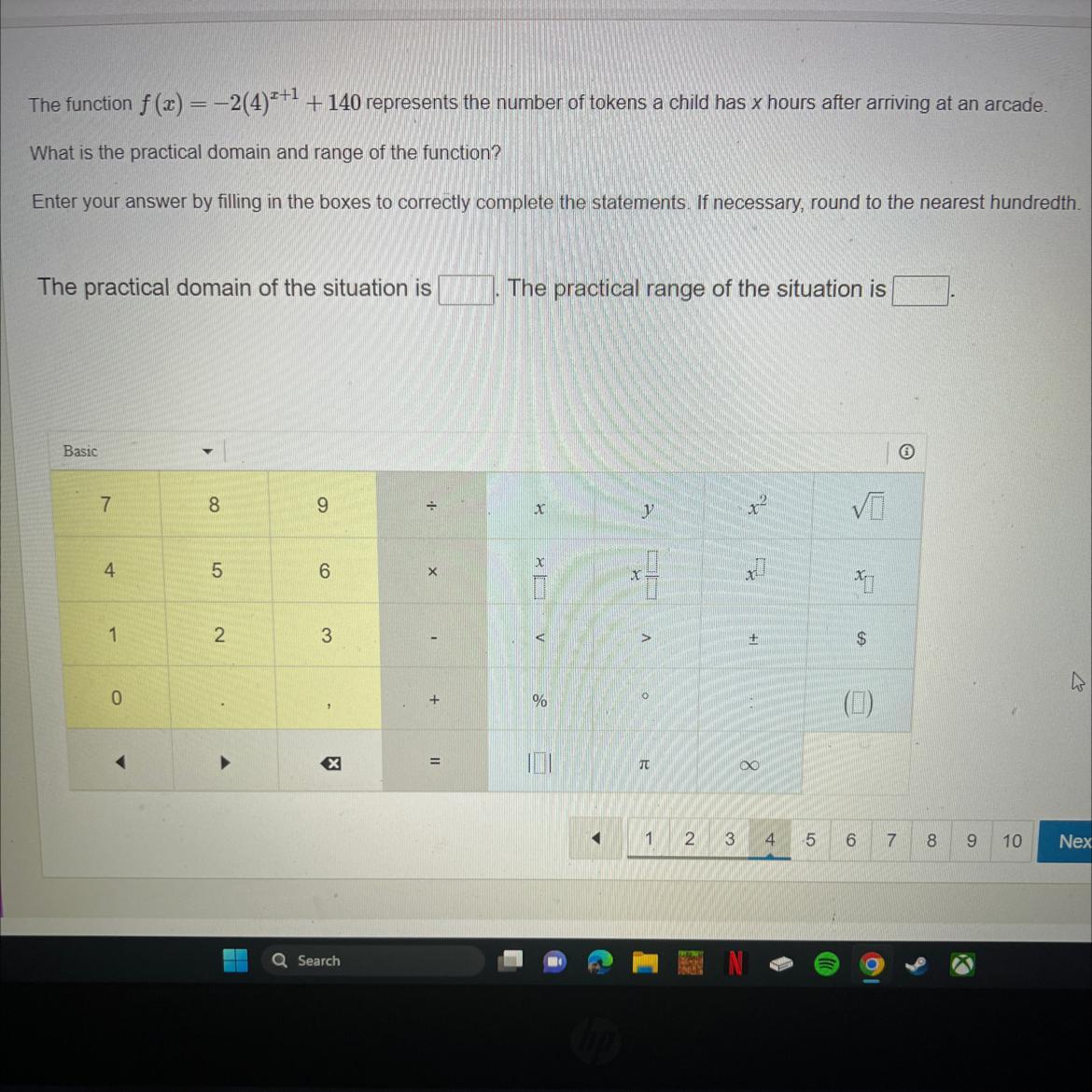
The function f(x) = -2(4)²+1 +140 represents the number of tokens a child has x hours after arriving at an arcade.
What is the practical domain and range of the function?
Enter your answer by filling in the boxes to correctly complete the statements. If necessary, round to the nearest hundredth.
The practical domain of the situation is ?
The practical range of the situation is ?
Answers
The practical domain of the situation is all real numbers, since there is no restriction on the number of hours the child can spend at the arcade.
The practical range of the situation is [1,140], since the minimum value of the function is 1 and the maximum value is 140.
3. What is the volume of the prism?
5.1 in
13.6 in
4.6 in
2.1 in
2.8 in

Answers
Answer:
102.19 cubic inches
Step-by-step explanation:volume =cross-section area * Length
cross-section area= (5.1 *4.6)+((13.6-4.6)*2.8)= 23.46 + 25.2= 48.66 square inches.
Length we take 2.1 in
volume = 46.66 * 2.1in = 102.19 cubic inches
how many ft is equal to 1.66m
Answers
Answer:
5.44 meters
Step-by-step explanation:
We Know
0.3048 meter = 1 ft
How many ft makes a height of 1.66m?
We Take
1.66 ÷ 0.3048 ≈ 5.44 meters
So, the answer is 5.44 meters.
find the area of the shaded region

Answers
Answer:
22 cm²Step-by-step explanation:
Shaded area is the difference of the bigger circle and two smaller ones:
A = π(3²) - 2π(1²) = 7π = 7*3.14 ≈ 22 cm²The locations of student desks are mapped using a coordinate plane where the origin represents the center of the classroom. Maria's desk is located at (2, −1), and Monique's desk is located at (−2, 5). If each unit represents 1 foot, what is the distance from Maria's desk to Monique's desk?
square root of 10 feet
square root of 20 feet
square root of 52 feet
square root of 104 feet
Answers
The distance from Maria's desk to Monique's desk is \(2\sqrt{13}\)
Given,
In the question:
Maria's desk is located at (2, −1), and Monique's desk is located at (−2, 5).
To find the distance from Maria's desk to Monique's desk.
Now, According to the question:
We know that :
The formula of Distance:
\(\sqrt{(x_{2} -x_{1} )^2+(y_{2}-y_{1} )^2}\)
Substitute (2, -1) and (-2, 5) into distance formula:
\(\sqrt{(-2-2)^2+(5+1)^2}\)
Calculate:
\(\sqrt{(-4)^2+(6)^2}\)
\(\sqrt{16+36}\\ \\\sqrt{52}\)
= \(2\sqrt{13}\)
Hence, The distance from Maria's desk to Monique's desk is \(2\sqrt{13}\)
Learn more about Distance Formula at:
https://brainly.com/question/21484248
#SPJ1
Answer: square root of 52
Step-by-step explanation:
did the practice test
12.874 rounded to the nearest tenth
Answers
I think it might be 12.9
Can anyone show how to solve these two questions. Thank you!

Answers
according the given question the exact value of given expression is \($\cos\frac{x}{2} = -\sqrt{\frac{1}{2(1 - \left(-\frac{160}{81}\right)^2)}} = -\sqrt{\frac{81^2}{2(81^2 - 160^2)}} = \boxed{-\frac{81\sqrt{239}}{319}}$\)
First, we need to find \($\sin x$\) using the identity\($\cos^2x + \sin^2x = 1$:$\sin^2x = 1 - \cos^2x = 1 - \left(-\frac{4}{5}\right)^2 = \frac{9}{25}$\)
Since \($\frac{\pi}{2} < x < \pi$\), we know that \($\frac{\pi}{4} < \frac{x}{2} < \frac{\pi}{2}$\). Therefore, we can use the
identity \($\tan\frac{x}{2} = \frac{\sin x}{1 + \cos x}$\):
\($\tan\frac{x}{2} = \frac{\sqrt{\frac{9}{25}}}{1 - \frac{4}{5}} = \frac{\frac{3}{5}}{\frac{1}{5}} = \boxed{3}$\)
\(If $\tan x = \frac{40}{9}$ and $\pi < x < \frac{3\pi}{2}$, find $\cos\frac{x}{2}$.\)
First, we need to find \($\sin x$\) using the identity \($\tan^2x + 1 = \sec^2x$\):
\($\sin x = \frac{\tan x}{\sec x} = \frac{\frac{40}{9}}{-\frac{9}{40}} = -\frac{160}{81}$\)
\(Since $\pi < x < \frac{3\pi}{2}$, we know that $\frac{\pi}{2} < \frac{x}{2} < \frac{3\pi}{4}$\). Therefore, we can use the identity \($\cos\frac{x}{2} = \pm\sqrt{\frac{1 + \cos x}{2}}$\):
\($\cos\frac{x}{2} = -\sqrt{\frac{1 + \cos x}{2}} = -\sqrt{\frac{1 + \frac{\cos^2x}{\sin^2x}}{2}} = -\sqrt{\frac{\sin^2x + \cos^2x}{2\sin^2x}} = -\sqrt{\frac{1}{2(1 - \sin^2x)}}$\)
Plugging in \($\sin x = -\frac{160}{81}$\) , we get:
\($\cos\frac{x}{2} = -\sqrt{\frac{1}{2(1 - \left(-\frac{160}{81}\right)^2)}} = -\sqrt{\frac{81^2}{2(81^2 - 160^2)}} = \boxed{-\frac{81\sqrt{239}}{319}}$\)
To know more about problems related to expression , click here:
https://brainly.com/question/16804733
#SPJ1
Abigail drove 84 miles in 4 hours. If she continued at the same rate, how far would she travel in 14 hours?
Answers
Answer:
210 miles
Step-by-step explanation:
84 divided by 4 equals 21
21 times 10 equals 210
Answer:
205 miles
Step-by-step explanation:
If the 14 hours is including the hours Abigail has already driven, then she would travel 121 miles for the six hours, for a combined total of 205 miles.
A forest covers 44,000 acres. A survey finds that 0.4% of the forest is old-growth trees. How many
acres of old-growth trees are there?
Answers
Answer:
0.4%*44000=1760 acres
Step-by-step explanation:
Match each expression with A, B, C or D.
A=a^3
B=6a
C=12a
D=3a^2
i)3a x 4
ii)a^2xa
iii) 6 1/2 a^2

Answers
The matching expressions are:
\(i) 3a x 4 = C (12a)\\ii) a^2 x a = A (a^3)\\iii) 6 × 1/2 a^2 = D (3a^2)\)
i) 3a x 4 can be represented as C (12a) since multiplying 3a by 4 gives 12a.
ii) a^2 x a can be represented as A (a^3) since multiplying a^2 by a gives a^3.
iii) \(6 \times 1/2 a^2\) can be represented as D (3a^2) since multiplying 6 by 1/2 and then by a^2 gives 3a^2.
To understand the matching expressions, let's break down each one:
i) 3a x 4:
This expression represents multiplying a variable, 'a', by a constant, 4. The result is 12a, which matches with C (12a).
ii) a^2 x a:
This expression represents multiplying the square of a variable, 'a', by 'a' itself. This results in a^3, which matches with A (a^3).
iii) 6 × 1/2 a^2:
This expression involves multiplying a constant, 6, by a fraction, 1/2, and then multiplying it by the square of 'a', a^2. The final result is 3a^2, which matches with D (3a^2).
Therefore, the matching expressions are:
i) 3a x 4 = C (12a)
ii) a^2 x a = A (a^3)
iii) 6 × 1/2 a^2 = D (3a^2)
for such more question on matching expressions
https://brainly.com/question/12270624
#SPJ8
Expand the function.
f(x) = (3x-4)4
81x4 − 432x³ + [? ]x²
+
-
X +
PLS HELP
Answers
The expansion of the function \((3x - 4)^4\) simplifies to \(81x^4 - 432x^3 + 864x^2 - 768x + 256.\)
To expand the function \(f(x) = (3x - 4)^4\), we can use the binomial theorem. According to the binomial theorem, for any real numbers a and b and a positive integer n, the expansion of \((a + b)^n\) can be written as:
\((a + b)^n = C(n, 0)a^n b^0 + C(n, 1)a^{(n-1)} b^1 + C(n, 2)a^{(n-2)} b^2 + ... + C(n, n-1)a^1 b^{(n-1)} + C(n, n)a^0 b^n\)
where C(n, k) represents the binomial coefficient, which is given by C(n, k) = n! / (k!(n-k)!).
Applying this formula to our function \(f(x) = (3x - 4)^4\), we have:
\(f(x) = C(4, 0)(3x)^4 (-4)^0 + C(4, 1)(3x)^3 (-4)^1 + C(4, 2)(3x)^2 (-4)^2 + C(4, 3)(3x)^1 (-4)^3 + C(4, 4)(3x)^0 (-4)^4\)
Simplifying each term, we get:
\(f(x) = 81x^4 + (-432x^3) + 864x^2 + (-768x) + 256\)
Therefore, the expanded form of the function \(f(x) = (3x - 4)^4\) is \(81x^4 - 432x^3 + 864x^2 - 768x + 256\).
Note that the coefficient of \(x^3\) is -432, the coefficient of \(x^2\) is 864, the coefficient of x is -768, and the constant term is 256.
For more question on function visit:
https://brainly.com/question/11624077
#SPJ8
Note the complete question is
![Expand the function.f(x) = (3x-4)481x4 432x + [? ]x+-X + PLS HELP](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/GfWbZg9TGTD1FI7gZnK9lbVdLBpjkw5X.jpeg)
Geometry proofs lm no
Answers
Answer:
?
Step-by-step explanation:
what is the answer to d and e?

Answers
Answer:
multiply!!
Step-by-step explanation:
just multiply for number 4 :)
At a sports event, a fair coin is flipped to determine which team has possession of the ball to start. The coin has two sides, heads, (H), and tails, (T). Identify the correct experiment, trial, and outcome below: Select all that apply: a. The experiment is identifying whether a heads or tails is flipped. b. The experiment is flipping the coin c. A trial is flipping a heads. d. A trial is one flip of the coin. e. An outcome is flipping a tails. f. An outcome is flipping a coin once.
Answers
The correct answer about experiment, trial, and outcome is
a. The experiment identifies whether a head or tail
b. The experiment is flipping the coin
d. A trial is one flip of the coin
Experiment:
An experiment in probability is a process or activity that involves observing or measuring an outcome or event, in order to determine the likelihood or probability of certain outcomes.
Outcome:In probability, an outcome refers to a possible result that can occur from an experiment or event. It is one of the possible outcomes that can happen, and it may be a single result or a set of results.
TrialIn probability, a trial is a single repetition of an experiment or event. It is the process of observing or measuring the outcome of an event or experiment once.
Here we have
At a sports event, a fair coin is flipped to determine which team has possession of the ball.
The coin has two sides, heads, (H), and tails, (T).
From the given options correct answers are
a. The experiment identifying whether a head or tail is flipped is correct because the experiment is to determine which side of the coin will be facing up after the coin is flipped, either heads (H) or tails (T).
b. The experiment is flipping the coin is correct because the experiment involves physically flipping the coin.
d. A trial is one flip of the coin is correct as a trial is defined as a single performance of an experiment, in this case, flipping the coin once.
Therefore,
The correct answer about experiment, trial, and outcome is
a. The experiment identifies whether a head or tail
b. The experiment is flipping the coin
d. A trial is one flip of the coin
Learn more about Probability at
https://brainly.com/question/30034780
#SPJ1
Test the claim about the difference between two population means
μ1
and
μ2
at the level of significance
α.
Assume the samples are random and independent, and the populations are normally distributed.Claim:
μ1=μ2;
α=0.01
Population statistics:
σ1=3.6,
σ2=1.4
Sample statistics:
x1=18,
n1=27,
x2=20,
n2=26
Determine the alternative hypothesis.
Ha:
μ1
▼
greater than>
greater than or equals≥
less than<
less than or equals≤
not equals≠
μ2
Determine the standardized test statistic.
z=nothing
(Round to two decimal places as needed.)
Determine the P-value.
P-value=nothing
(Round to three decimal places as needed.)
What is the proper decision?
A.Fail to reject
H0.
There is enough evidence at the
1%
level of significance to reject the claim.
B.Reject
H0.
There is enough evidence at the
1%
level of significance to reject the claim.
C.Fail to reject
H0.
There is not enough evidence at the
1%
level of significance to reject the claim.
D.Reject
H0.
There is not enough evidence at the
1%
level of significance to reject the claim
Answers
The correct answer is Option C. The proper decision, in this case, is "Fail to reject H0. There is not enough evidence at the 1% level of significance to reject the claim."
The alternative hypothesis, in this case, is "μ1 ≠ μ2", as the claim being tested is that the two population means are equal.
To calculate the standardized test statistic, we can use the following formula:
z = (x1 - x2) / sqrt(((σ1^2) / n1) + ((σ2^2) / n2))Substituting in the values given in the problem, we get:
z = (18 - 20) / sqrt(((3.6^2) / 27) + ((1.4^2) / 26))
z = (-2) / sqrt((12.96 / 27) + (1.96 / 26))
z = (-2) / sqrt(0.481 + 0.075)
z = (-2) / sqrt(0.556)
z = (-2) / 0.746
z = -2.67
To calculate the P-value, we can use the standard normal table to look up the probability of getting a value of -2.67 or lower if the null hypothesis were true. The P-value in this case would be the probability of getting a value equal to -2.67 or lower, plus the probability of getting a value equal to 2.67 or higher.
Using the standard normal table, we find that the probability of getting a value equal to -2.67 or lower is 0.0039, and the probability of getting a value equal to 2.67 or higher is 0.9961. Therefore, the P-value is 0.0039 + 0.9961 = 1.0000.
Since the P-value is equal to 1.0000, which is greater than the level of significance α = 0.01, we fail to reject the null hypothesis.
Learn more about alternative hypothesis here:
https://brainly.com/question/13045159
#SPJ4
Tina left her house at 6:45 AM.
She came home at 1:35 PM.
How long was she out of the
house?
Answers
Answer:
MY ANSWER IS 5:10
Step-by-step explanation:
HOPE HELPFUL MARK ME BRAINLIESTTina was out of the house for 7 hours 10 minutes.
What does x time same as cash mean?"x time same as cash" means that you got x time to pay the cash without any additional cost. If you take more time than x time to pay the due amount, then you would have to pay extra.
Tina left the house to go to work at = 6 : 45 AM
She gets back to home at = 1:35 PM or 13 :35 PM
We have to calculate the time she is out of the house.
Now ,we subtract the departure time from the arrival time.
= 13 : 35 - 06 : 45
= 07 : 10 hours
Hence, Tina was out of the house for 7 hours 10 minutes.
Learn more about work and time here:
https://brainly.com/question/1063042
#SPJ2
shareholders. Calculate the amount of dividend r of dividend received by Bishwant. Curriculum Development Centre. Sanothimi. Bhaktanur 65 Vedanta Excel in Mathematics - Booeceived by Mrs. Rai. b) A Business Company sold 2,500 shares at Rs 1,200 per share. Bishwant bought 450 shares. If the company earned a net profit of Rs 39,00.000 in a year and it announced to distribute 18% dividend from the net profit to its shareholders, find the amount
Answers
3900000×18% = 702000
702000÷2500 = 280.8 per share dividend
450×280.8 = 126360