Answers
Answer: x in top right = 90°
x in bottom left = 90°
Step-by-step explanation:
The vertical angle of 110° = 110°. That angle is corresponding to x + 20°
110° - 20° = 90°
We know all of the interior angles of the triangle because:
1. Vertical angle to 20° = 20°
2. Supplementary angle to 110° = 70°
3. Other angle = 180 - 20 - 70 = 90°
The supplement to 90° = 90° , so the x in the bottom left = 90°
I am not a professional, simply using prior knowledge!
Note- It would mean the world to me if you could mark me brainliest!
Related Questions
ill mark brainlist plss help

Answers
Answer:
kilometers
Step-by-step explanation:
I hope it´s right for you
2^3 + (-16) / 4^2 x 5 - (-3)
Answers

What is $15 with a 10% how much does he pay with the discount
Answers
Answer:
66.666666666667%
Step-by-step explanation:
Mayumi plans to buy pencils and a notebook at the school store. A pencil costs $0.15, and a The notebook costs $1.59. Mayumi has $5.00. Which inequality could she use to find the number of pencils she can buy? in equation please
Answers
Answer: 0.15p+1.59n ≤ 5.00
Step-by-step explanation:
Given: A pencil costs $0.15, and a The notebook costs $1.59.
Let p = Number of pencils.
n = Number of notebooks.
Total cost of pencil and notebook = 0.15p+1.59n
Since Mayumi has $5.00.
So, Total cost of pencil and notebook ≤ $5.00
⇒ 0.15p+1.59n ≤ 5.00
Hence, the required inequality: 0.15p+1.59n ≤ 5.00
Find x (circle)
(Btw I don’t know if 5.6 is correct so just ignore that)

Answers
Answer:
A. 11.2
Step-by-step explanation:
But this has nothing to do with 5.6 × 2. Erase that! Lol.
You have a right triangle here. The only thing to do with the circle is that there are two radii (plural of radius) shown. So they have to be the same measure.
The unmarked "bottom" of the triangle, the short leg, is a radius, so it too, is 8.4.
The hypotenuse of the right triangle, the side on the right, the longest side is 5.6 + 8.4.
The hypotenuse is 14.
Let's do some Pythagorean Theorem.
Leg^2+ leg^2=hypotenuse^2
you know,
a^2 + b^2 = c^2
fill in what we know.
8.4^2 + b^2 = 14^2
simplify.
70.56 + b^2 = 196
subtract 70.56
b^2 = 125.44
squareroot both sides
b = 11.2
What is the constant up a proportionally in a equation y=x/g
Answers
Answer:
Step-by-step explanation:
\(y=(\frac{1}{g} )x\)
Constant up a proportionally is \(\frac{1}{g}\).
the sum of 5 times a number and 23
Answers
Answer:
5n+23
Step-by-step explanation:
five times a number is 5n and 23 is +3
5n is 5 times a number and +23 is and 23
QUICK! 40 points. Consider this cone with the diameter measure of 17 inches.
A cone with diameter 17 inches and slant height of 22 inches.
What is the surface area of the cone?
SA = Pir2 + Pirl
A. 204Pi in.2
B. 259.25Pi in.2
C. 446.25Pi in.2
D. 663Pi in.2

Answers
259.25π in² is the surface area of the cone
The surface area of a cone can be calculated using the formula SA = πr² + πrl
where r is the radius and l is the slant height.
Given that the diameter is 17 inches, the radius (r) is half of the diameter, which is 17/2 = 8.5 inches.
The slant height (l) is given as 22 inches.
Substituting these values into the formula:
Surface Area = π(8.5)² + π(8.5)(22)
= 72.25π + 187π
= 259.25π
Therefore, the surface area of the cone is 259.25π in²
To learn more on Three dimensional figure click:
https://brainly.com/question/2400003
#SPJ1
Suppose y varies directly with x. When x is 5, y is 15. What is y when x is 12?
Answers
Answer:
y = 36
Step-by-step explanation:
given y varies directly with x then the equation relating them is
y = kx ← k is the constant of variation
to find k use the condition when x = 5 , y = 15
15 = 5k ( divide both sides by 5 )
3 = k
y = 3x ← equation of variation
when x = 12 , then
y = 3 × 12 = 36
f(x)= a(x+p)² +q and g(x)= 0 3 3.1 x + p 1. The turning point of f is (1;4) and the asymptotes of g intersect at the turning point of f. Both graphs cut the y-axic at 3. 3.2 3.3 3.4 a 10 g +94 (1:4) Determine the equation of f Determine the equation of g Determine the coordinates of the x-intercept of g For which values of x will f(x) ≥ g(x)? [9]
Answers
Step-by-step explanation:
Let's solve the given questions step by step:
1. Determine the equation of f:
From the given information, we know that the turning point of f is (1, 4). The general form of a quadratic function is f(x) = ax^2 + bx + c. We are given that f(x) = a(x + p)^2 + q, so let's substitute the values:
f(x) = a(x + p)^2 + q
Since the turning point is (1, 4), we can substitute x = 1 and f(x) = 4 into the equation:
4 = a(1 + p)^2 + q
This gives us one equation involving a, p, and q.
2. Determine the equation of g:
The equation of g is given as g(x) = 0.3x + p1.
3. Determine the coordinates of the x-intercept of g:
The x-intercept is the point where the graph of g intersects the x-axis. At this point, the y-coordinate is 0.
Setting g(x) = 0, we can solve for x:
0 = 0.3x + p1
-0.3x = p1
x = -p1/0.3
Therefore, the x-intercept of g is (-p1/0.3, 0).
4. For which values of x will f(x) ≥ g(x)?
To determine the values of x where f(x) is greater than or equal to g(x), we need to compare their expressions.
f(x) = a(x + p)^2 + q
g(x) = 0.3x + p1
We need to find the values of x for which f(x) ≥ g(x):
a(x + p)^2 + q ≥ 0.3x + p1
Simplifying the equation will involve expanding the square and rearranging terms, but since the equation involves variables a, p, and q, we cannot determine the exact values without further information or constraints.
To summarize:
We have determined the equation of f in terms of a, p, and q, and the equation of g in terms of p1. We have also found the coordinates of the x-intercept of g. However, without additional information or constraints, we cannot determine the exact values of a, p, q, or p1, or the values of x for which f(x) ≥ g(x).
Please help me with this proof.

Answers
Answer:
See below
Step-by-step explanation:
For the second step, \(\angle T\cong\angle R\) by Alternate Interior Angles. The rest of the steps appear to be correct.
Could you guys answer this for me by 12am!
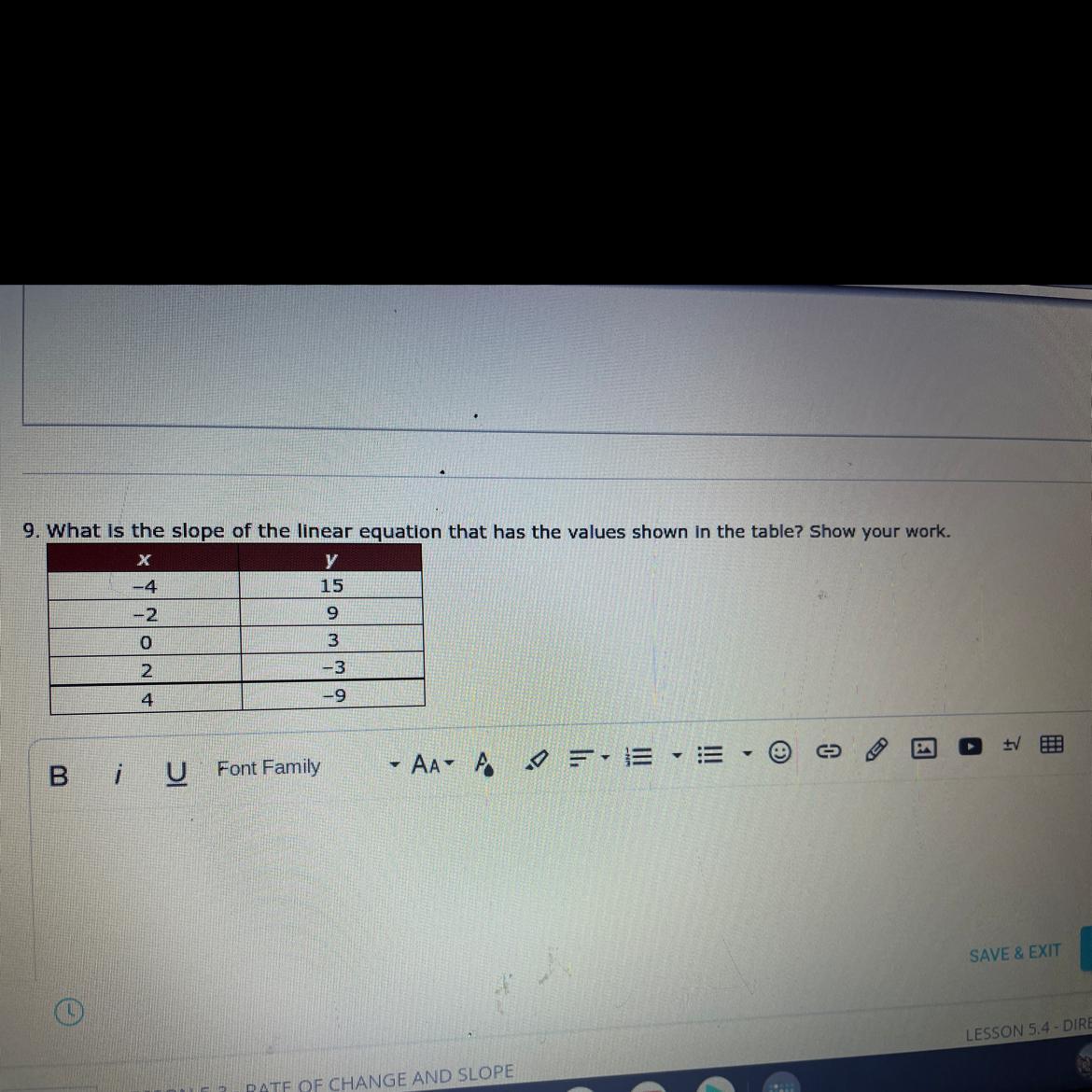
Answers
Answer:
-3
Step-by-step explanation:
Slope is y2 - y1 / x1 - x2.
So, let's take two random points; I have chosen (0, 3) and (2, -3).
Excellent. Let's calculate the slope.
Slope = (-3 - 3) / (2 - 0) = -6 / 2 = -3.
Hope this helps!
Find the slope of a line parallel
to 2y= 6x+8
Answers
The slope of a line parallel to 2y= 6x+8 is 3.
How to calculate or determine the slope of a line?In Mathematics and Geometry, the slope of any straight line can be determined by using the following mathematical equation;
Slope (m) = (Change in y-axis, Δy)/(Change in x-axis, Δx)
Slope (m) = rise/run
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
In Mathematics and Geometry, parallel lines are two (2) lines that are always the same (equal) distance apart and never meet. Therefore, two (2) lines are parallel under the following conditions:
m₁ = m₂
By making y the subject of formula, we have:
2y = 6x + 8
y = 3x + 4
Therefore, the slope is 3.
Read more on slope here: brainly.com/question/3493733
#SPJ1
Which of the following is equivalent to 2 x (4 x 3)? *
2 + (4 + 3)
2 x (6 x 4)
(2 x 4) x 3
8
Answers
2×(4×3)?24
4×3=12
12×2=24
(2×4)×3=24
ayudaaa a resolver esto plis

Answers
The value of x in degrees will be 6° and 11° using properties of parallel lines.
What Qualities Characterize Parallel Lines?They are typically equal-distance, parallel straight lines. The lines here are parallel. They never come together no matter how far you extend them in any one way.
Pairs of equal-sized angles that are both obtuse or acute and are generated on the same side of the transversal are known as corresponding angles. Each pair of comparable angles on the same side of the crossing transversal is equal to the other.
The alternative angle theorem states that alternate interior angles or alternate exterior angles that come from cutting two parallel lines are congruent.
In the above figure,
8x + 7 = 55
8x = 55 - 7
x = 6
Measure of the angle will be 8 × 6 + 7 = 49
In 11)
10x + 10 = 9x + 21 (by using first corresponding angles and then alternate angles)
⇒x = 11
The value of x in degrees will be = 11° using properties of parallel lines.
To learn more about Parallel lines refer to :
brainly.com/question/16701300
#SPJ1
The machinery in a cereal plant fills 350 g boxes of cereal. The specifications for the machinery permit for a certain amount of fill tolerance. It is found that the weights of filled cereal boxes are normally distributed with a mean of 350 g and a standard deviation of 4 g. What is the probability that a box of cereal is under filled by 5 g or more?
Answers
There is approximately an 89.44% probability that a box of cereal is underfilled by 5 g or more.
To find the probability that a box of cereal is underfilled by 5 g or more, we need to calculate the probability of obtaining a weight measurement below 345 g.
First, we can standardize the problem by using the z-score formula:
z = (x - μ) / σ
Where:
x = the weight value we want to find the probability for (345 g in this case)
μ = the mean weight (350 g)
σ = the standard deviation (4 g)
Substituting the values into the formula:
z = (345 - 350) / 4 = -1.25
Next, we can find the probability associated with this z-score using a standard normal distribution table or a statistical calculator.
The probability of obtaining a z-score less than -1.25 is approximately 0.1056.
However, we are interested in the probability of underfilling by 5 g or more, which means we need to find the complement of this probability.
The probability of underfilling by 5 g or more is 1 - 0.1056 = 0.8944, or approximately 89.44%.
Therefore, there is approximately an 89.44% probability that a box of cereal is underfilled by 5 g or more.
For more questions on probability
https://brainly.com/question/251701
#SPJ8
Calculus 2
Use the Trapezoidal Rule, the Midpoint Rule, and Simpson's Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.)
\(\int\limits^4_1 7\sqrt{ln(x)} \, dx\) , n=6
Answers
Answer:
See Below.
Step-by-step explanation:
We want to estimate the definite integral:
\(\displaystyle \int_1^47\sqrt{\ln(x)}\, dx\)
Using the Trapezoidal Rule, Midpoint Rule, and Simpson's Rule with six equal subdivisions.
1)
The trapezoidal rule is given by:
\(\displaystyle \int_{a}^bf(x)\, dx\approx\frac{\Delta x}{2}\Big(f(x_0)+2f(x_1)+...+2f(x_{n-1})+f(x_n)\Big)\)
Our limits of integration are from x = 1 to x = 4. With six equal subdivisions, each subdivision will measure:
\(\displaystyle \Delta x=\frac{4-1}{6}=\frac{1}{2}\)
Therefore, the trapezoidal approximation is:
\(\displaystyle =\frac{1/2}{2}\Big(f(1)+2f(1.5)+2f(2)+2f(2.5)+2f(3)+2f(3.5)+2f(4)\Big)\)
Evaluate:
\(\displaystyle =\frac{1}{4}(7)(\sqrt{\ln(1)}+2\sqrt{\ln(1.5)}+...+2\sqrt{\ln(3.5)}+\sqrt{\ln(4)})\\\\\approx18.139337\)
2)
The midpoint rule is given by:
\(\displaystyle \int_a^bf(x)\, dx\approx\sum_{i=1}^nf\Big(\frac{x_{i-1}+x_i}{2}\Big)\Delta x\)
Thus:
\(\displaystyle =\frac{1}{2}\Big(f\Big(\frac{1+1.5}{2}\Big)+f\Big(\frac{1.5+2}{2}\Big)+...+f\Big(\frac{3+3.5}{2}\Big)+f\Big(\frac{3.5+4}{2}\Big)\Big)\)
Simplify:
\(\displaystyle =\frac{1}{2}(7)\Big(f(1.25)+f(1.75)+...+f(3.25)+f(3.75)\Big)\\\\ =\frac{1}{2}(7) (\sqrt{\ln(1.25)}+\sqrt{\ln(1.75)}+...+\sqrt{\ln(3.25)}+\sqrt{\ln(3.75)})\\\\\approx 18.767319\)
3)
Simpson's Rule is given by:
\(\displaystyle \int_a^b f(x)\, dx\approx\frac{\Delta x}{3}\Big(f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+...+4f(x_{n-1})+f(x_n)\Big)\)
So:
\(\displaystyle =\frac{1/2}{3}\Big((f(1)+4f(1.5)+2f(2)+4f(2.5)+...+4f(3.5)+f(4)\Big)\)
Simplify:
\(\displaystyle =\frac{1}{6}(7)(\sqrt{\ln(1)}+4\sqrt{\ln(1.5)}+2\sqrt{\ln(2)}+4\sqrt{\ln(2.5)}+...+4\sqrt{\ln(3.5)}+\sqrt{\ln(4)})\\\\\approx 18.423834\)
(6-2x) +(15-3x) where x=0.2
Answers
\( \sf{\blue{«} \: \pink{ \large{ \underline{A\orange{N} \red{S} \green{W} \purple{E} \pink{{R}}}}}}\)
Expression: \(\displaystyle\sf (6-2x) +(15-3x)\)
Substituting \(\displaystyle\sf x=0.2\):
\(\displaystyle\sf (6-2(0.2)) +(15-3(0.2))\)
Simplifying the expression inside the parentheses:
\(\displaystyle\sf (6-0.4) +(15-0.6)\)
\(\displaystyle\sf 5.6 +14.4\)
Calculating the sum:
\(\displaystyle\sf 20\)
Therefore, \(\displaystyle\sf (6-2x) +(15-3x)\) evaluated at \(\displaystyle\sf x=0.2\) is equal to \(\displaystyle\sf 20\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
which of the following is true:
A. 59 + 59 = 108
B. 20 + 19 = 49
C. 32 + 34 = 76
D. 30 + 32 = 62
Answers
Please mark me as Brainliest.Thank you and hope it helps!
prove that there exist only five regular polyhedron
Answers
To prove that there are only these five regular polyhedra, we can consider Euler's polyhedron formula, which states that for any convex polyhedron, the number of vertices (V), edges (E), and faces (F) satisfy the equation V - E + F = 2.
Proving there exist Five Regular PolyhedronThe five regular polyhedra, also known as the Platonic solids, are the only convex polyhedra where all faces are congruent regular polygons, and the same number of polygons meet at each vertex.
The five regular polyhedra are:
1. Tetrahedron: It has four triangular faces, and three triangles meet at each vertex.
2. Cube: It has six square faces, and three squares meet at each vertex.
3. Octahedron: It has eight triangular faces, and four triangles meet at each vertex.
4. Dodecahedron: It has twelve pentagonal faces, and three pentagons meet at each vertex.
5. Icosahedron: It has twenty triangular faces, and five triangles meet at each vertex.
To prove that there are only these five regular polyhedra, we can consider Euler's polyhedron formula, which states that:
"for any convex polyhedron, the number of vertices (V), edges (E), and faces (F) satisfy the equation V - E + F = 2".
For regular polyhedra, each face has the same number of sides (n) and each vertex is the meeting point of the same number of edges (k). Therefore, we can rewrite Euler's formula for regular polyhedra as:
V - E + F = 2
=> kV/2 - kE/2 + F = 2
=> k(V/2 - E/2) + F = 2
Since each face has n sides, the total number of edges can be calculated as E = (nF)/2, as each edge is shared by two faces. Substituting this into the equation:
k(V/2 - (nF)/2) + F = 2
=> (kV - knF + 2F)/2 = 2
=> kV - knF + 2F = 4
Now, we need to consider the conditions for a valid polyhedron:
1. The number of faces (F), edges (E), and vertices (V) must be positive integers.
2. The number of sides on each face (n) and the number of edges meeting at each vertex (k) must be positive integers.
Given these conditions, we can analyze the possibilities for different values of n and k. By exploring various combinations, it can be proven that the only valid solutions satisfying the conditions are:
(n, k) pairs:
(3, 3) - Tetrahedron
(4, 3) - Cube
(3, 4) - Octahedron
(5, 3) - Dodecahedron
(3, 5) - Icosahedron
Therefore, there exist only five regular polyhedra.
Learn more about regular polyhedron here:
https://brainly.com/question/29134238
#SPJ1
A ladder of length (2x+6) feet is positioned x feet from a wall. If the ladder reaches a height of (2x+4) feet along the wall. Find the longest leg.
A. 10ft
B. 24ft
C. 26ft
D. 13cm
Answers
Using the Pythagoras theorem, the longest leg has the length of 24 feet.
Given that,
A ladder of length (2x+6) feet is positioned x feet from a wall.
Height of the ladder = (2x + 6) feet
Distance of ladder from the wall = x feet
Height of the wall that the ladder is placed = (2x + 4) feet
These three lengths form s right triangle where (2x + 6) feet is the hypotenuse.
Longest leg is (2x + 4) feet
Using the Pythagoras theorem,
(2x + 6)² = (2x + 4)² + x²
4x² + 24x + 36 = 4x² + 16x + 16 + x²
4x² + 24x + 36 = 5x² + 16x + 16
x² - 8x - 20 = 0
(x - 10) (x + 2) = 0
x = 10 or x = -2
x = 2 is not possible.
So x = 10
Longest leg = 2x + 4 = 20 + 4 = 24 feet
Hence the length of the longest leg is 24 feet.
Learn more about Pythagoras theorem here :
https://brainly.com/question/343682
#SPJ1
What should be subtracted from minus 3 / 4 so has to get 5 / 6 ?
Answers
Answer:
Step-by-step explanation:
Step 1:First Make 3/4 and 5/6 into like fractions.Find the L.C.M of 4 and
6,which is 12.
3*3/4*3=9/12
5*2/6*2=10/12
Step 2:Subtract 9/12 from 10/12,which is 1/12.
Please can somebody help me to solve this one? I been trying but it’s not 12. It has to be something else…

Answers
The area of the whole is: 5×3=15
The area of the triangle is: 2×3/2=3
So the area of the shades region is 15-3=12
Help please!
S = 180m
How many strides would a runner take during a 1-hour run (60 min)
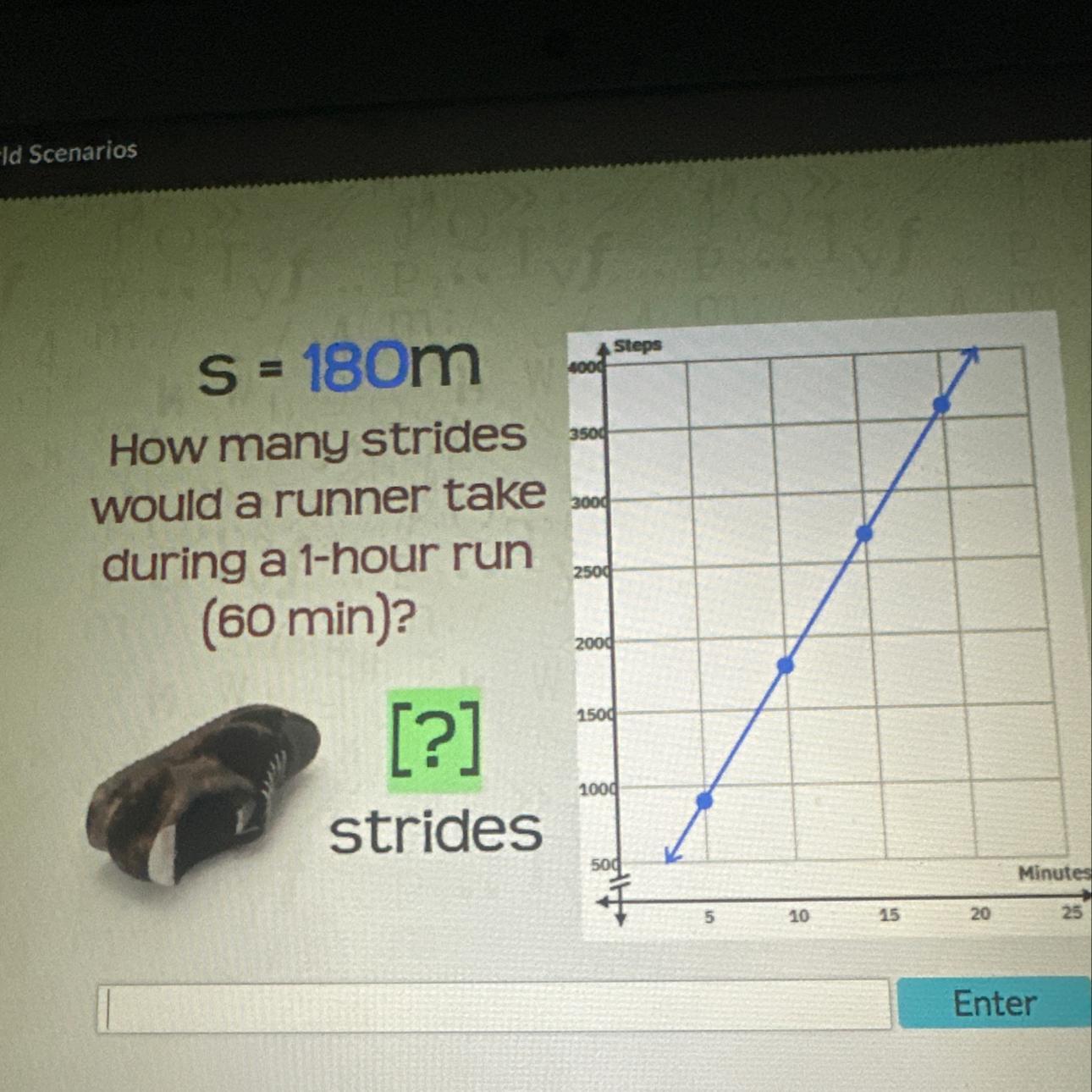
Answers
The number of strides the runner will make during 1 hour run will be =
10,800.
How to calculate the total number of strides made by the runner in a hour?To calculate the distance or number of strides made by the runner in an
hour, the graph given above is considered as follows;
The y-axis which represents the number of strides is plotted against the x-axis which is the number of hours.
From the graph
20 minutes= 3600 strides
60 minutes = X strides
make X the subject of formula;
x= 3600×60/20
= 216000/20
= 10,800
Learn more about distance here:
https://brainly.com/question/30694816
#SPJ1
How many
1/5s are in 9?
A.5/9
B.9/5
C.45
D.4 1/2
Answers
Answer:
C 45
Step-by-step explanation:
Answer:
Answer and explanation
9 ÷ 1/59 × 5/1= 45A sculpture is in the shape of a square pyramid. The sculpture has a height of 36 feet and a volume of 19,200 cubic feet. Find the side length of the square base
Answers
Answer:
40ft
Step-by-step explanation:
The volume of a square pyramid is given by:
\(V=\frac{l^2h}{3}\)
where V is the volume, l is the length of the square base, and h is the height.
Since we need to find the length, we solve for \(l\) in the last equation:
\(l^2h=3V\\\\l^2=\frac{3V}{h} \\\\l=\sqrt{\frac{3V}{h} }\)
and now, we substitute the known values:
\(V=19,200ft^3\\h=36ft\)
and we get the following:
\(l=\sqrt{\frac{3(19,200ft^3)}{36ft} }\\ \\l=40ft\)
the length of the square base is 40ft
Which statement describes the transformation of figure 2 into figure 3?

Answers
Answer:
2 reflection across the y axis
question is in the image below

Answers
The perimeter of Sam's string is 178 inches.
Given information:
Sam has a rectangular shaped window.
Length = 65 inches.
Width = 24 inches.
To find the perimeter:
you can use the formula:
Perimeter = 2 x (Length + Width)
Substituting the values into the formula, we have:
Perimeter = 2 x (65 + 24)
Perimeter = 2 x 89
Perimeter = 178 inches
Therefore, the perimeter of the rectangular window is 178 inches.
So, the perimeter of the rectangular window is 178 inches. This means that if you were to walk along the outline of the window, you would cover a total distance of 178 inches. It's important to note that the perimeter represents the total length of all the sides combined, and it is measured in the same unit (in this case, inches) as the length and width of the window.
To learn more about the rectangular perimeter;
https://brainly.com/question/22109593
#SPJ1
Kacie is constructing the inscribed circle for △MNP. She constructed the angle bisectors of angle M and angle N and labeled the intersection of the bisectors as point A.Which construction is a correct next step for Kacie?Open the compass to the width of AM¯¯¯¯¯¯ and draw a circle centered at point A.Open the compass to the width of , A M ¯ , and draw a circle centered at point , A, .Construct the perpendicular bisector of AM¯¯¯¯¯¯ .Construct the perpendicular bisector of , A M ¯ , .Open the compass to the width of AP¯¯¯¯¯ and draw a circle centered at point A.Open the compass to the width of , A P ¯ , and draw a circle centered at point , A, .Construct the line that passes through point A and is perpendicular to NP¯¯¯¯¯¯ .

Answers
From the statement, we know that:
• Kacie is constructing the inscribed circle for △MNP,
,• she constructed the angle bisectors of angle M and angle N,
• and labelled the intersection of the bisectors as point A.
(1) Now, Kacy must construct a perpendicular from the centre point to one side of the triangle.
(2) After this, she must place the compass on the centre point while adjusting its length to the point where the perpendicular crosses the triangle.
(3) Finally, she must draw the inscribed circle.
So the answer is that Kacy must construct the perpendicular bisector of AM.
AnswerConstruct the perpendicular bisector of AM
need help i dont understand

Answers
Answer:
Step-by-step explanation:
it would be "c" because the question asks for the number that makes the inequality true
4x≤ x+3
the graph in c is saying that every number that is 1 or less than 1 makes the inequality true. so lets take -7 as an example
4 x -7=-28
-28+3=-25
-25 is greater than -28 so the inequality is true. the reason why graph d doesnt work is because if we plug in 2 into the equation, then 4x =8 and x+3=5
5 is not greater than 8 so it doesnt work
