Answers
Answer:
24 25 26
Step-by-step explanation:
guess and check..................
Related Questions
HELP PLS I NED THIS LUV U GUUS

Answers
Answer:
\((x-h)^{2} + (y-k)^{2} = r^{2}\)
Step-by-step explanation:
Using the digits 1 to 9, without repeating any numbers, place a digit in each box that will create 3 equivalent ratios.

Answers
6:3 = 14:7 = 58:29
hope this is helpful!
19) Mr. Kelly finds a nice little bank (GOLIATH NATIONAL BANK) to invest the money he made from his
DAD-PUN-A-DAY calendar sales. He puts in $4,500 initially in an account that pays 24% interest
compounded quarterly. How long will it take for his money to reach the $15,000 he needs to buy some
real jokes?
Answers
Answer:
Step-by-step explanation:
Answer: it will take 17.5 years to double his money in the account.
Step-by-step explanation:
We would apply the formula for determining compound interest which is expressed as
A = P(1+r/n)^nt
Where
A = total amount in the account at the end of t years
r represents the interest rate.
n represents the periodic interval at which it was compounded.
P represents the principal or initial amount deposited
From the information given,
P = $500
A = 500 × 2 = $1000
r = 4% = 4/100 = 0.04
n = 4 because it was compounded 3 times in a year.
Therefore,.
1000 = 500(1 + 0.04/4)^4 × t
1000/500 = (1 + 0.01)^4t
2 = (1.01)^4t
Taking log of both sides, it becomes
Log2 = 4tlog 1.01
0.301 = 4t × 0.0043 = 0.0172t
t = 0.301/0.0172
t = 17.5 years
Sarah can text 91 words in 14 minutes. At
this rate, how many minutes would it take
her to text 65 words?
Answers
If Sarah can text 91 words in 14 minutes, then at this rate she will type 65 words in 10 minutes
Number of minutes to types 91 words = 14 minutes
Here we have to use the unitary method to solve the problem
Time taken to type 1 word = Number of minutes to types 91 words / 91
Substitute the values in the equation
= 14 / 91
= 2 / 13
Time taken to type 65 words = Time taken to type 1 word × 65
Substitute the values in the equation
= (2/13) × 65
= 10 minutes
Hence, if Sarah can text 91 words in 14 minutes, then at this rate she will type 65 words in 10 minutes
Learn more about unitary method here
brainly.com/question/22056199
#SPJ1
The drama club had a 'Yard Clean Up' day to earn money for their next production. At the end of the day, they had earned a total of $480. How much money did they have after they subtracted the amount they spent for the trash cans and plastic bags? What other information is needed to solve this problem? 1. The number of yards they cleaned up 2. The cost of the trash cans and plastic bags 3. The number of people who were working 4. The cost of cleaning up one yard
Answers
Answer:
2). The cost of the trash cans and plastic bags.
Step-by-step explanation:
As per the details provided, the information regarding 'the cost incurred on buying the trash cans, as well as, plastic bags for the cleanup process' is very necessary to find the money left with the drama club from their earnings. The amount they earned within the day is given and the amount left is being asked in the question post the expenditure of the cans and plastic bags for the cleaning process. To subtract the incurred expense from the total earnings, one will need information regarding the cost of those bags and cans. Thus, option 2 is the correct answer.
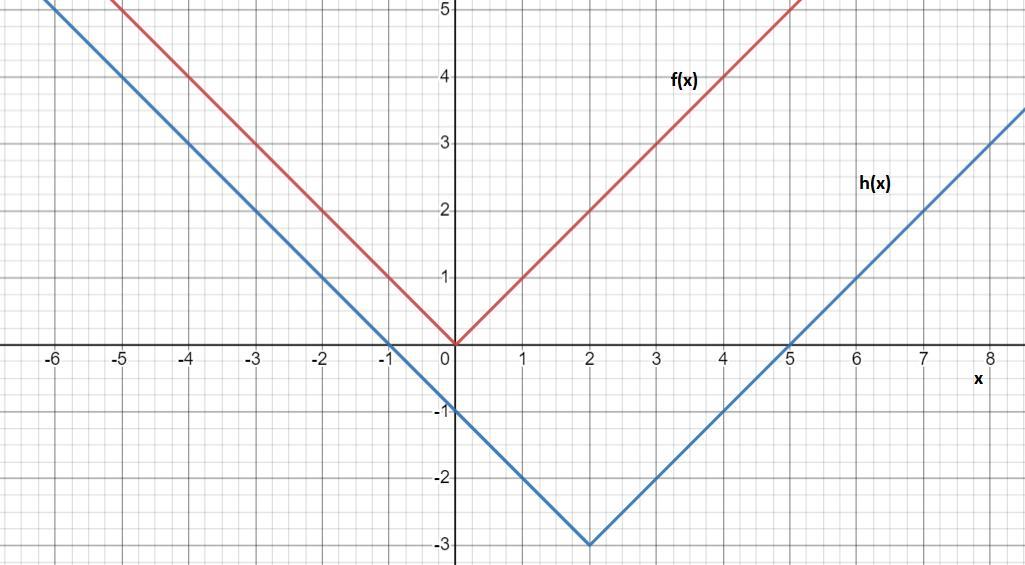
3. The function h(x) is a transformed function of f(x) = |x|. The transformation is as follows: 3 units vertical shift down, 2 units horizontal shift right.
a. Write the transformed equation, h(x).
b. Graph f(x) and h(x) on the same coordinate plane. Be sure to label the functions f(x) and h(x). This must be graphed by hand or by using the tools in Word. You may not use a web-based graphing program.
Answers
a. The transformed equation is given as follows: h(x) = |x - 2| - 3.
b. The graph of the two functions is shown by the image presented at the end of the answer.
What are translations?The translations are movements to the triangle in each of these directions:
Up.Down.Left.Right.The parent function in this problem is given as follows:
f(x) = |x|.
The first translation was a vertical translation three units down, hence we have that:
g(x) = f(x) - 3 = |x| - 3.
The second translation was a horizontal translation two units right, hence the have that the definition of the transformed equation h(x) is given as follows:
h(x) = g(x - 2) = |x - 2| - 3.
The graph of the functions is given by the image shown at the end of the answer, and the translations are verified on every point of the function, but especially the vertices.
More can be learned about translations at https://brainly.com/question/29211183
#SPJ1
15 points for anwser
Determine whether each expression is equivalent to x^(7/4).
Expression Yes No
√(7&x^4 )
∜(x^7 )
(∜x)^7
√(x^(7/4) )
∜(x^5 )∙∜(x^2 )
√(5&x^4 )∙√(2&x^4 )
(∜x)^7/(√x)^0
Help.
Answers
Answer:
Step-by-step explanation:
Michelle has $8 and wants to buy a combination of dog food to feed at least two dogs at the animal shelter. A serving of dry food costs $1, and a serving of wet food costs $3. This system of inequalities models the scenario: x + 3y ≤ 8 x + y ≥ 2 Part A: Describe the graph of the system of inequalities, including shading and the types of lines graphed. Provide a description of the solution set. (4 points) Part B: Is the point (8, 2) included in the solution area for the system? Justify your answer mathematically. (3 points) Part C: Choose a point in the solution set and interpret what it means in terms of the real-world context. (3 points)
Answers
Part A: The shaded region represents the feasible region where both inequalities are satisfied simultaneously. It is below the line x + 3y = 8 and above the line x + y = 2.
Part B: The point (8, 2) is not included in the solution area.
Part C: The point (3, 1) represents one feasible solution that meets the constraints of the problem.
Part A: The graph of the system of inequalities consists of two lines and a shaded region. The line x + 3y = 8 is a solid line because it includes the equality symbol, indicating that points on the line are included in the solution set. The line x + y = 2 is also a solid line. The shaded region represents the feasible region where both inequalities are satisfied simultaneously. It is below the line x + 3y = 8 and above the line x + y = 2.
Part B: To determine if the point (8, 2) is included in the solution area, we substitute the x and y values into the inequalities:
8 + 3(2) ≤ 8
8 + 6 ≤ 8
14 ≤ 8 (False)
Since the inequality is not satisfied, the point (8, 2) is not included in the solution area.
Part C: Let's choose a point in the solution set, such as (3, 1). This point satisfies both inequalities: x + 3y ≤ 8 and x + y ≥ 2. In the context of the real-world scenario, this means that Michelle can buy 3 servings of dry food (x = 3) and 1 serving of wet food (y = 1) with her $8 budget. This combination of dog food allows her to feed at least two dogs at the animal shelter while staying within her budget. The point (3, 1) represents one feasible solution that meets the constraints of the problem.
For more such questions on feasible region
https://brainly.com/question/29084868
#SPJ8
How do you calculate rate of change?

Answers
Change in the Independent Variable / Change in the Dependent Variable
hope this helps!!
Answer:
The calculation for ROC is simple in that it takes the current value of a stock or index and divides it by the value from an earlier period. Subtract one and multiply the resulting number by 100 to give it a percentage representation.
Step-by-step explanation:
The volume of a rectangular prism is 945 ft. If it has a length of 15 ft and a width of 9 ft, what is
its height?
Answers
Answer: 7ft
Step-by-step explanation:
Rectangular Prism = L x W x H
135H = 945
H = 7 ft
(4) let (s) be a sequence satisfying |sn 2 - sn 11 ≤|sn 1-snl for all n € n. e (a) show that sm 1 - sml≤2·2-m|s₂ s₁ for all m e n. | s₁ for all n>m > 1. (b) show that isn - sml≤4.2m|s₂ -
Answers
To prove the given statements, we will use the triangle inequality property, which states that for any real numbers a, b, and c:
|a + b| ≤ |a| + |b|
|a - b| ≤ |a| + |b|
(a) To prove sm+1 - sm ≤ 2·2^(-m)·|s₂ - s₁| for all m ∈ ℕ, we will use the given inequality |sn+2 - sn+1| ≤ |sn+1 - sn|.
Let's consider m ∈ ℕ. Using the given inequality, we can write:
|sm+1 - sm| ≤ |sm - sm-1|
≤ |sm-1 - sm-2|
≤ ...
≤ |s₂ - s₁|
Since we have |s₂ - s₁| on the right side, we can substitute it into the inequality:
|sm+1 - sm| ≤ |s₂ - s₁|
Now, we need to prove that |s₂ - s₁| ≤ 2·2^(-m)·|s₂ - s₁|. Let's multiply both sides of the inequality by 2^m:
2^m·|s₂ - s₁| ≤ 2·2^(-m)·|s₂ - s₁|
Since 2^m·2^(-m) = 2^(m-m) = 2^0 = 1, the inequality becomes:
|s₂ - s₁| ≤ 2·2^(-m)·|s₂ - s₁|
Therefore, we have shown that sm+1 - sm ≤ 2·2^(-m)·|s₂ - s₁| for all m ∈ ℕ.
(b) To prove |sn - sm| ≤ 4·2^m·|s₂ - s₁| for all n > m > 1, we can use the same approach as in part (a).
Let's consider n > m > 1. Using the given inequality, we can write:
|sn - sm| ≤ |sn - sn-1|
≤ |sn-1 - sn-2|
≤ ...
≤ |sm+1 - sm|
Using the inequality from part (a), we can substitute it into the inequality:
|sn - sm| ≤ |sm+1 - sm|
≤ 2·2^(-m)·|s₂ - s₁|
Now, we need to prove that 2·2^(-m)·|s₂ - s₁| ≤ 4·2^m·|s₂ - s₁|. Let's simplify this inequality:
2·2^(-m)·|s₂ - s₁| ≤ 4·2^m·|s₂ - s₁|
Since 2^(-m)·2^m = 2^(-m+m) = 2^0 = 1, the inequality becomes:
|s₂ - s₁| ≤ 4·2^m·|s₂ - s₁|
Therefore, we have shown that |sn - sm| ≤ 4·2^m·|s₂ - s₁| for all n > m > 1.
Learn more about inequalities in Mathematics: https://brainly.com/question/30238989
#SPJ11
A rectangular solid with sides a and b, and with a height of 20 cm has a volume of 120 cm³. Find the formula which defines b in terms of a. Why is this formula an indirect proportion? What is the domain of this function? A rectangular solid with sides a and b, and with a height of 20 cm has a volume of 120 cm³. Find the formula which defines b in terms of a. Why is this formula an indirect proportion? What is the domain of this function?
Answers
120 = ab(20)
Simplifying this equation, we get:
b = 6/a
Therefore, the formula that defines b in terms of a is b = 6/a.
This formula is an indirect proportion because as the value of a increases, the value of b decreases, and vice versa. In other words, the product of a and b is constant (in this case, 120), so if one of the variables increases, the other must decrease to maintain the same product.
The domain of this function is all positive real numbers except for a = 0, since division by zero is undefined. Therefore, the domain of the function is (0, ∞).
I
Simplify the expression.
2/5y−4+7−9/10y =
Answers
Step:

Find the distance between the two points in simplest radical form.

Answers
The distance bewteen the points (-3,5) and (3,1) in a simple radical form is 2√13.
What is the distance between the given points?The distance formula used in finding the distance between two points is expressed as;
d = √( ( x₂ - x₁ )² + ( y₂ - y₁ )² )
From the graph;
Point A: (-3,5)
x₁ = -3
y₁ = 5
Point B: (3,1)
x₂ = 3
y₂ = 1
Plug the given values into the distance formula and simplify.
\(d = \sqrt{( x_2 - x_1)^2 + (y_2 -y_1 )^2} \\\\d = \sqrt{( 3-(-3))^2 + (1 -5)^2} \\\\d = \sqrt{( 3+ 3)^2 + (1 -5)^2} \\\\d = \sqrt{( 6)^2 + (-4)^2} \\\\d = \sqrt{36 + 16} \\\\d = \sqrt{52}\\\\d = 2\sqrt{13}\)
Therefore, the distance between the points is 2√13.
Learn more about the distance formula here: brainly.com/question/24509115
#SPJ1
Omg guys I need help with this question I've failed the test like 4 time because of this question and I give up. Can someone please help me with this?

Answers
Answer:
D. 270
Step-by-step explanation:
With the information given you can work your way around the table to fill in the blanks
300-120=180 Red-footed one-headed
180+200=380 total red-footed
650-380=270 total black-footed (answer)
270-120=150 black-footed two-headed
150+200=350 two-headed
Answer:
270
Step-by-step explanation:
300-120=180,to get one headed red footed
650-300=350, total two headed.
350-200=150, to get two headed black footed.
150+120=270, total black footed mizjigs
1. Consider
dt
dy
=f(t,y),y(0)=y
0
. where f(t,y)=
2
1
(y+1)(3−y)t,y
0
=1 (a) (2 pts) Solve this initial value problem and write its exact solution y(t). (b) (5 pts) Use Euler's method with h=0.1 to obtain a numerical solution u(t) at t=3 and plot the numerical solution u(t) (solid line) along with the exact solution y(t) (dashed line) for 0≤t≤3. (c) (3 pts) Compute the error e
1
defined by e
1
=max∣u(t)−y(t)∣(0≤t≤3) for h=0.1, 0.05, and 0.025, and make a table showing the variation of e
1
with h. What do you observe? 2. Consider the second-order Runge-Kutta method (or improved Euler's Method), which is given by v
n+1
=v
n
+
2
h
(k
1
+k
2
), where k
1
=f(t
n
,v
n
),k
2
=f(t
n
+h,v
n
+hk
1
). (a) (7 pts) For the initial value problem considered in Problem 1, find a numerical solution v(t) at t=3 with h=0.1 and plot the numerical solution v(t) (solid line) along with the exact solution y(t) (dashed line) for 0≤t≤3. (b) (3pts) Compute the error e
2
defined by e
2
=max∣v(t)−y(t)∣(0≤t≤3) for h=0.1, 0.05, and 0.025, and make a table showing the variation of e
2
with h. What is the difference between the two numerical methods?
Answers
In problem 1, an initial value problem is given with a first-order differential equation. The exact solution, y(t), is obtained, and Euler's method is used with different step sizes to obtain numerical solutions, u(t), at t=3.In problem 2, the second-order Runge-Kutta method (improved Euler's method) is applied to the same initial value problem. The numerical solution, v(t), is obtained at t=3 with h=0.1.
In problem 1, the initial value problem is solved analytically to obtain the exact solution, y(t). Euler's method is then applied with different step sizes (h) to approximate the solution numerically at t=3. The numerical solution, u(t), is plotted alongside the exact solution, y(t), to visualize their comparison. The error, e1, is calculated as the maximum absolute difference between u(t) and y(t) over the interval [0, 3]. By varying the step size and computing e1, the effect of the step size on the accuracy of the numerical solution can be observed.
In problem 2, the second-order Runge-Kutta method is employed to approximate the solution numerically. The numerical solution, v(t), is computed at t=3 with h=0.1 and compared to the exact solution, y(t), through a plot. The error, e2, is calculated as the maximum absolute difference between v(t) and y(t) over the interval [0, 3]. By computing e2 for different step sizes and comparing it to e1 from problem 1, the difference between the two numerical methods can be observed in terms of accuracy and convergence.
Learn more about Euler's method here:
https://brainly.com/question/30699690
#SPJ11
Assuming that the tire mileage is normally distributed and the mean number of miles to failure is not known and a known 6 = 3,700 miles. Using your sample of 41 tires as your estimate of the mean (X Bar): what is the upper and lower bound of a 95% confidence interval? (This was your Question #2): Suppose when you did this this calculation you found the ERROR to be too large and would like to limit the error to 1000 miles. What should my sample size be? 42 46 53
48
Answers
To find the upper and lower bounds of a 95% confidence interval, we need to use the sample mean (X), sample standard deviation (s), and the sample size (n).
Given that the sample mean (X) is not provided in the question, we cannot calculate the confidence interval. Please provide the value of the sample mean.
Regarding the second part of the question, to limit the error to 1000 miles, we need to calculate the required sample size (n) using the formula:
n = (Z * s / E)^2
Where Z is the z-score corresponding to the desired confidence level (in this case, 95%), s is the sample standard deviation, and E is the desired maximum error (1000 miles).
Since the sample standard deviation (s) is not provided, we cannot calculate the required sample size. Please provide the value of the sample standard deviation or any additional relevant information to proceed with the calculations.
To know more about deviation visit-
brainly.com/question/15313381
#SPJ11
I need some help with this.

Answers
Answer: 23
Step-by-step explanation:
The range of the data set is the same thing as subtracting the smallest value from the largest value.
Here, our smallest value is 8 and our largest value is 31.
31 - 8 = 23
This data set has a range of 23.
6 Given: TY XY, ZTVY = ZXWY Prove: ATVY = AXWY Statements Reasons 1. TY ~ XY 1. Given 2. Given 2. LTVY & LXWY 3. 3. 4. 4. 5. 5. OTVY Z OXWY Gina wison All Things Aige
Answers
Statement 3:
\(TV\cong XW\)Reason: Law of cosines
Statement 4:
\(VY\cong WY\)Reason: Law of cosines
Proof
We have the following situation:
Because the law of cosines,
\(\begin{gathered} a^2=c^2+d^2-2cd\cos (b) \\ a^2=e^2+f^2-2ef\cos (b) \end{gathered}\)Therefore,
\(c^2+d^2-2cd\cos (b)=e^2+f^2-2ef\cos (b)\)
5m 10m 4m what is the area of this
Answers
Answer: 200m^3
Step-by-step explanation:
Rectangular prism (Cuboid) formula - L * W * H Length × Width × Height
10m(5m)(4m) = 200m^3
A restaurant offers a catering service which costs $16.50 per person with a $74.75 service charge. For parties of 40 or more people, a group discount applies, and the cost is $11.75 per person along with the service charge dropping to $37.00. Write a piecewise-defined function which calculates the total cost, T, (in dollars) of the catering service, which serves n people.
Answers
Answer:
16.50+91.25=91.25
91.25×40=3650
11.75-37.00=-25.25
Total cost, T of the catering service, which serves n people = T = 16.50n + 74.75 and T = 11.75n + 37.00
Given,
Charges per person = 16.50
Service charges = 74.75
Let n be the number of the people,
Let T be the total cost
Now, according to the given question,
T = 16.50n + 74.75
If n>=40
T = 11.75n + 37.00
So, we have 2 equations which define the total cost -
T = 16.50n + 74.75,
T = 11.75n + 37.00
To learn more about linear equations from the given link
https://brainly.com/question/2030026
#SPJ4
I am between 30 and 50.
The sum of my digits is 10.
My ones digit is greater than
my tens digit. I am not 37.
Who am I?
Answers
See explanation
Explanation:
The sun of my digits is ten. So the number could be 37 or 46, which match the criteria of both the first sentence and the second.
But if it’s not 37, then it must be 46, which should be your answer.
data from the bureau of labor statistics indicates that in a certain month, 38.1% of the labor force had a high school diploma or fewer years of education, 29.6% had some college or an associate's degree, and 32.3% had a bachelor's degree or more education. of those with a high school diploma or fewer years of education, 5.1% were unemployed. of those with some college or an associate's degree, 3.5% were unemployed, and of those with a bachelor's degree or more education, 2.8% were unemployed. find the probability that a randomly chosen labor force participant has a high school diploma or less education given that he or she is unemployed. the probability is (type an integer or decimal rounded to three decimal places as needed.)
Answers
The probability that a randomly chosen labor force participant has a high school diploma or fewer years of education given that he or she is unemployed is approximately 0.999 or 99.9%.
To find the probability that a randomly chosen labor force participant has a high school diploma or fewer years of education given that he or she is unemployed, we can use Bayes' theorem.
Let's define the following events:
A: Labor force participant has a high school diploma or fewer years of education.
B: Labor force participant is unemployed.
We are looking for P(A|B), the probability that a labor force participant has a high school diploma or fewer years of education given that he or she is unemployed.
According to the information given:
P(A) = 0.381 (38.1% of the labor force has a high school diploma or fewer years of education)
P(B|A) = 0.051 (5.1% of those with a high school diploma or fewer years of education are unemployed)
P(B) = (P(A) * P(B|A)) + (P(A') * P(B|A')) [using the Law of Total Probability]
P(A') = 1 - P(A) = 1 - 0.381 = 0.619 (complement of having a high school diploma or fewer years of education)
P(B|A') = 0.035 (3.5% of those with some college or an associate's degree are unemployed)
P(B|A) = 0.028 (2.8% of those with a bachelor's degree or more education are unemployed)
Substituting these values into the equation for P(B):
P(B) = (0.381 * 0.051) + (0.619 * 0.035)
Now we can calculate P(A|B) using Bayes' theorem:
P(A|B) = (P(B|A) * P(A)) / P(B)
Substituting the values we have:
P(A|B) = (0.051 * 0.381) / P(B)
Calculating P(B):
P(B) = (0.381 * 0.051) + (0.619 * 0.035) = 0.019431
Substituting the calculated value of P(B) into the equation for P(A|B):
P(A|B) = (0.051 * 0.381) / 0.019431 ≈ 0.999
Therefore, the probability that a randomly chosen labor force participant has a high school diploma or fewer years of education given that he or she is unemployed is approximately 0.999 or 99.9%.
To learn more about Bayes' theorem visit:
brainly.com/question/32765058
#SPJ11
Help!
What is one and sixty-seven hundredths added to fifteen and nine tenths?
Answers
suppose that k is a proper subgroup of h and h is a proper subgroup of g. if |k| 5 42 and |g| 5 420, what are the possible orders of h?
Answers
The order of h can be any factor of 420 between 43 and 419, inclusive. This is because k is a proper subgroup of h, which means that |k| is a factor of |h|. Since |k| is greater than or equal to 5 and |g| is 420, the maximum possible order of h is 419 (since |h| cannot be equal to |g|). Similarly, the minimum possible order of h is 43 (since |h| cannot be equal to |k|). Therefore, the possible orders of h range from 43 to 419, inclusive, and can be any factor of 420 within this range.
Given that k is a proper subgroup of h and h is a proper subgroup of g, we know that |k| is a factor of |h| and |h| is a factor of |g|. Also, we are given that |k| is greater than or equal to 5 and |g| is 420. Therefore, the maximum possible order of h is 419 (since |h| cannot be equal to |g|), and the minimum possible order of h is 43 (since |h| cannot be equal to |k|).
Now, we need to find the possible orders of h between 43 and 419, inclusive. The factors of 420 within this range are: 43, 46, 69, 83, 138, 207, and 419. Hence, the possible orders of h can be any of these factors.
To sum up, the possible orders of h are any factors of 420 between 43 and 419, inclusive. The maximum possible order is 419, and the minimum possible order is 43. This is because k is a proper subgroup of h, which means that |k| is a factor of |h|, and |g| is 420. Therefore, h can have any factor of 420 within the given range.
To know more about factors visit:
https://brainly.com/question/28983916
#SPJ11
3. Find the area of the region bounded by the curves: a. y=x+3 and y=x2+1. b. y2=x+5 and x=2y+3
Answers
Area of the region bounded by the curves y = x + 3 and y = x² + 1 is (14/3) square units and area of the region bounded by these curves y² = x + 5 and x = 2y + 3 is 150/3 square units.
To find the area of the region bounded by the curves y = x + 3 and y = x² + 1,
we first need to find their intersection points.
x + 3 = x² + 1⇒ x² - x - 2
= 0⇒ (x - 2) (x + 1)
= 0x = 2 or x = -1
So, the intersection points are (-1, 2) and (2, 5).
Now, we can integrate to find the area:
A = ∫(-1)²+1 (x + 3) dx + ∫2¹( x² + 1) dx
= [(x²/2) + 3x] (-1)²+1 + [(x³/3) + x] 2¹
= (14/3) square units
To find the area of the region bounded by the curves y² = x + 5 and x = 2y + 3, we first need to sketch the curves.
We can do this by rewriting the equation of the second curve in terms of y as :
y = (x - 3)/2
Now, we can plot these curves:
Plotting these curves, we can see that they intersect at (7, 2) and (-3, -2).
To find the area of the region bounded by these curves, we can integrate:
A = ∫-3¹ (y² - 5) dy + ∫2¹ ((y + 3)/2) dy
= [(y³/3) - 5y] -3¹ + [(y²/2) + (3/2)y] 2¹
= 150/3 square units.
Learn more about Integral from the given link :
https://brainly.com/question/30094386
#SPJ11
how much time would a core 10 meters in lenght represent if it contained 5 meters of red ooze and 5 meters of red clay
Answers
If a core 10 meters in length contains 5 meters of red ooze and 5 meters of red clay, each meter in the core would represent half a meter of red ooze and half a meter of red clay.
To calculate the representation of each meter in the core, we divide the total length of each material (5 meters) by the total length of the core (10 meters).
For red ooze:
Representation of each meter = (Length of red ooze) / (Total length of core)
= 5 meters / 10 meters
= 0.5 meters
For red clay:
Representation of each meter = (Length of red clay) / (Total length of core)
= 5 meters / 10 meters
= 0.5 meters
Therefore, each meter in the core would represent half a meter of red ooze and half a meter of red clay.
In a core 10 meters in length containing 5 meters of red ooze and 5 meters of red clay, each meter of the core would represent half a meter of red ooze and half a meter of red clay. This calculation assumes an equal distribution of the materials throughout the core length.
To know more about length visit:
https://brainly.com/question/30680391
#SPJ11
Using the spinner above, what
is the probability of not spinning
a 4?
Answers
The probability of not spinning a 4 is 5/6 or 0.83
To calculate the probability of not spinning a 4, we need to first determine the total number of possible outcomes. The spinner shown has six equal sections, which means there are six possible outcomes in total.
Out of the six sections, only one section has a number 4 on it. Therefore, the probability of spinning a 4 is 1/6.
To find the probability of not spinning a 4, we need to subtract the probability of spinning a 4 from 1.
1 - 1/6 = 5/6
Therefore, the probability of not spinning a 4 is 5/6 or 0.83 (rounded to two decimal places). This means that if we were to spin the spinner multiple times, we can expect to not spin a 4 in about 83% of the spins.
It's important to note that this probability assumes that the spinner is fair and unbiased, meaning each section has an equal chance of being selected.
To know more about probability visit: https://brainly.com/question/30034780
#SPJ11
Write the equation of each line given the y-intercept and x-
Answers
The equation of each line given the y-intercept and x-intercept
5 and -4 is 4y- 20 = 5x.
The line has an x-intercept at x = -4 and y intercept at y = 5 this means that the line passes through the points(,0) and(,5).
Now we find the pitch m of the line passing through the points(,0) and(,5)(x-intercept).
The pitch of the line is
m = y2- y1/ x2- x1
= 5- 0/ 0-(- 4)
= 5/ 4
Point- pitch Formula y = m(x-x1)
where m is the pitch and( x, y) is the given point.
Now substituting the values
y- 0 = (5/4)( x-(- 4))
y = (5/4)( x 4)
4y- 20 = 5x
Learn more about equation of line here :
https://brainly.com/question/21511618
#SPJ4
The complete question :
Find the equation of the line that has an y intercept and x-intercept at
5 and -4.
The braking distance (dm) of a car is directly
proportional to the square of its speed (v m/s)
When the speed of the car is increased by
50%, what is the percentage change in its
braking distance?
Answers
Answer:
Step-by-step explanation:
We can assign variables as:
d = original breaking distance
b = original speed of the vehicle
d′ = increased breaking distance
b′ = increased speed of the vehicle
We can look at it this way, originally it was like this:
d=kb2
Now, if we increase the speed to b’ which 200% more than b, we will have
d′=k(b′)2
d′=k(b+2b)2
d′=k(3b)2
d′=9kb2
Obtaining the difference between d and d’, we have
d′−d=9kb2−kb2
d′−d=8kb2
in terms of d
d′−d=8(kb2)
d′−d=8d
Adding d on both sides of the equation,
d′=d+8d
Which means the original breaking distance is increased by 800%. This is similar to the phrase “the speed of the vehicle is increased by 200%” which translates to “b + 2b”.
Hope this answer helps you :)
Have a great day
Mark brainliest
There is a 100% increase in the braking distance after 50% increase in speed.
What is speed?A body is said to be of speed v m/s if it travels v meter per second.
How to solve it?The braking distance of a car is directly proportional to the velocity of its speed(v m/s)
When the speed of the car is increased by 50% then the speed of the car v m/s becomes (3v/2) m/s.
The braking distance of a car is directly proportional to the square of its speed hence, the braking distance becomes
v²c where c is some constant.
So, the braking distance after 50% of the car speed is increased becomes (3v/2)²c₁, where c₁ is some constant.
Hence, the percentage change in the car's braking distance is
\(\frac{\frac{9}{4}-\frac{3}{2}}{\frac{3}{2}}\)
\(=\frac{\frac{9-6}{4}}{\frac{3}{2}}\\=1\)
That means there is a 100% increase in the braking distance after 50% increase in speed.
Learn more about speed here-
brainly.com/question/7359669
#SPJ2
