Can someone help with this? Find the area of the shaded region. Anything helps, thank you

Answers
Thus, the Area of shaded region for the given sector of circle is found as:
1.14 sq. cm.
Explain about the sector of circle:Two radii that meet at the centre to form a sector define a circle. The sector is the portion of the circle created by these two radii. Knowing a circle's central angle measurement and radius measurement are both crucial for solving circle-related difficulties.
Given:
radius r = 2 cminternal angle Ф = 90 degreesArea of shaded region = area of sector - area of triangle
Area of shaded region = Ф/360° * (πr²) - 1/2*base*height
Area of shaded region = 90/360° * (3.14*2²) - 1/2*2*2
Area of shaded region = 1/4*3.14*4 - 2
Area of shaded region = 3.14 - 2
Area of shaded region = 1.14 sq. cm
Thus, the Area of shaded region for the given sector of circle is found as:
1.14 sq. cm.
Know more about the sector of circle:
https://brainly.com/question/22972014
#SPJ1
Related Questions
"
TECHNO ECONOMIC ANALYSIS OF A 6KW SOLAR PV PANEL with two
storage systems (i) Battery (ii) THERMAL ENERGY STORAGE SYSTEM
the load profile of the home is given below. PLEASE provide a
detailed analysis
000 UTAW Nm 0 0 A B 1 Hours Energy Consumption 2 0:00 0.45 3 1:00 0.4 4 2:00 0.4 5 3:00 0.4 6 4:00 0.4 7 5:00 0.3 8 6:00 0.3 9 7:00 0.45 10 8:00 0.65 11 9:00 0.85 12 10:00 0.95 13 11:00 0.99 14 12:001.05 15 13:00 1.1 16 14:00 1.2 17 15:00 1.3 18 16:00 1.9 19 17:00 2.16 20 18:00 2.2 21 19:00 2.15 22 20:00 1.95 23 21:00 1.9 24 22:00 1.8 25 23:00 1.45 26 26.7 27 Daily Energy Consumption (kWh)= 26.728 units 2.5 2 1.5 1 0.5 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 TIME
Answers
The given load profile indicates a daily energy consumption of 26.728 kWh for a home. A techno-economic analysis of a 6 kW solar PV panel system with battery and thermal energy storage can help optimize energy usage, reduce grid dependency during peak hours, and potentially provide backup power. Detailed analysis considering costs, efficiency, system lifespan, and available incentives is required for a comprehensive evaluation.
To perform a techno-economic analysis of a 6 kW solar PV panel system with battery and thermal energy storage, we will analyze the given load profile and consider the potential benefits and feasibility of the storage systems.
Load profile:Hours Energy Consumption (kWh)
0:00 0.45
1:00 0.4
2:00 0.4
3:00 0.4
4:00 0.4
5:00 0.3
6:00 0.3
7:00 0.45
8:00 0.65
9:00 0.85
10:00 0.95
11:00 0.99
12:00 1.05
13:00 1.1
14:00 1.2
15:00 1.3
16:00 1.9
17:00 2.16
18:00 2.2
19:00 2.15
20:00 1.95
21:00 1.9
22:00 1.8
23:00 1.45
From the load profile, we can identify the following:
The peak energy consumption occurs between 17:00 and 18:00, with a load of 2.2 kWh.The lowest energy consumption occurs between 5:00 and 6:00, with a load of 0.3 kWh.The total daily energy consumption is 26.728 kWh.Now let's consider the potential benefits and analysis of incorporating the storage systems:
(i) Battery Storage System:
A battery storage system can store excess energy generated by the solar PV panel system during the day and discharge it during periods of low solar generation or high energy consumption. It helps to mitigate the intermittency of solar energy and optimize self-consumption.
Benefits:
Load Shifting: The battery system can store energy during low-consumption periods and discharge it during peak consumption hours, reducing reliance on the grid.Backup Power: In case of grid outages, the battery can provide power to essential loads, ensuring uninterrupted electricity supply.Time-of-Use Optimization: If there are time-of-use electricity tariffs, the battery can help shift consumption to low-tariff periods, potentially saving costs.(ii) Thermal Energy Storage System:
A thermal energy storage system can store excess energy in the form of heat, which can be used for various purposes such as space heating, water heating, or other thermal energy needs in the home.
Benefits:
Demand Management: The thermal energy storage system can shift energy consumption for heating purposes to periods with excess solar generation, optimizing energy usage.Reduced Heating Costs: By utilizing stored thermal energy, the home can reduce its reliance on conventional heating methods, potentially lowering heating costs.Enhanced Energy Efficiency: The use of thermal energy storage allows for better energy utilization, reducing overall energy waste.To perform a detailed techno-economic analysis, the following factors need to be considered:
Solar PV Panel System Cost: The cost of installing a 6 kW solar PV panel system, including the panels, inverter, mounting hardware, and installation expenses.Battery Storage System Cost: The cost of the battery storage system, including batteries, inverters, control systems, and installation.Thermal Energy Storage System Cost: The cost of the thermal energy storage system, including storage tanks, heat exchangers, insulation, controls, and installation.System Lifespan: The expected lifespan of each system component to estimate the long-term benefits.System Efficiency: The efficiency of the solar PV panels, battery storage system, and thermal energy storage system in converting and storing energy.Energy Tariffs: The electricity tariffs and any incentives or net metering programs available to assess the financial benefits.Maintenance and Operating Costs: The ongoing maintenance and operational expenses associated with the systems.Financing Options: The availability of financing options, loans, or incentives that can impact the upfront investment and payback period.Government Incentives: Any available government subsidies, tax credits, or incentives for renewable energy installations.With this information, a comprehensive techno-economic analysis can be conducted to evaluate the feasibility, cost-effectiveness, and potential savings of the solar PV panel system with battery and thermal energy storage for the specific home and location.
To know more about load profile, refer to the link below:
https://brainly.com/question/28202638#
#SPJ11
the sample mean salary of 500 nba players is 5 million dollars. we also know that the population standard deviation is 0.7 million dollars. we want to construct a confidence interval for population mean with 95% confidence. what will be the length of our confidence interval (in terms of million dollars)?
Answers
The length of our confidence interval (in terms of million dollars) is (4.9412,5.0588)
A 95% confidence interval on the z-table is 1.96.
Now find the standard error using the formula: standard deviation / square root sample size:
0.7 / √500 = 0.03
Multiply to the confidence interval: 1.96 x 0.03 = 0.0588
Now add and subtract the average salary of the nba players:
5.0000 - 0.0588 = 4.9412(million dollar)
5.0000 + 0.0588 = 5.0588(million dollar)
The answer is 4.9412 ≤ u ≤ 5.0588(million dollar)
To Learn more about length of confidence interval question:
https://brainly.com/question/13029066
#SPJ4
2. Consider the function f(x)=x 2with domain D=R. (a) Determine the average rate of change in f(x) as x varies from x= 21to x= 23 . (b) Determine the instantaneous rate of change in f(x) at x=1.
Answers
The average rate of change in f(x) as x varies from 21 to 23 is 44. The instantaneous rate of change in f(x) at x = 1 is 2. These values represent the rates at which the function f(x) is changing over the specified intervals and points.
To determine the average rate of change in the function f(x) = x^2 as x varies from x = 21 to x = 23, and the instantaneous rate of change in f(x) at x = 1, we can apply the concept of the rate of change, which measures how a function changes with respect to its input.
(a) The average rate of change in f(x) over the interval [21, 23] is given by the formula:
Average Rate of Change = (f(23) - f(21)) / (23 - 21)
Substituting the values into the formula, we have:
Average Rate of Change = (23^2 - 21^2) / (23 - 21)
= (529 - 441) / 2
= 88 / 2
= 44
Therefore, the average rate of change in f(x) as x varies from 21 to 23 is 44.
(b) To determine the instantaneous rate of change in f(x) at x = 1, we can find the derivative of the function f(x) = x^2 and evaluate it at x = 1.
The derivative of f(x) = x^2 is given by:
f'(x) = 2x
Evaluating f'(x) at x = 1, we have:
f'(1) = 2(1)
= 2
Therefore, the instantaneous rate of change in f(x) at x = 1 is 2.
Learn more about Average Rate of Change here : brainly.com/question/13235160
#SPJ11
2 and 1/6 divided by 4 and 1/3, help pls
Answers
Answer:
The answer is 1 9/19
Step-by-step explanation:
The population of an island was 2 million in 1950. The population grew in an exponential trend for 63 years and became 6.5 million in 2013. It is estimated that the carrying capacity of the island is 10 million. Assuming the population growth rate in the future remains the same as in the last 50 years, what will be the population of the island in 2050? (Assume constant carrying capacity and consumption/capita.)
Answers
The population of an island in 1950 was 2 million. The population grew exponentially for 63 years and reached 6.5 million in 2013. The carrying capacity of the island is estimated to be 10 million.
If the population growth rate in the future is similar to the last 50 years, what will the population be in 2050
The population is given to be increasing exponentially, which means it will follow the equation:
\($P(t) = P_0 e^{rt}$\)Here,\($P(t)$\) is the population after a period of time \($t$, $P_0$\) is the initial population, $r$ is the annual growth rate (which we are given is the same as the growth rate of the last 50 years), and \($t$\) is the time.
We can find the annual growth rate $r$ using the formula:\($$r = \frac{\ln{\frac{P(t)}{P_0}}}{t}$$\)
We know\($P_0 = 2$ million, $P(t) = 6.5$ million, and $t = 63$\) years. Substituting these values, we get:
\($r = \frac{\ln{\frac{6.5}{2}}}{63} = 0.032$\) (rounded to 3 decimal places)
Since the carrying capacity of the island is 10 million, we know that the population will not exceed this limit.
Therefore, we can use the logistic model to find the population growth over time. The logistic growth model is:
\($$\frac{dP}{dt} = r P \left(1 - \frac{P}{K}\right)$$\)
where $K$ is the carrying capacity of the environment. This can be solved to give:\($P(t) = \frac{K}{1 + A e^{-rt}}$\)
where \($A = \frac{K-P_0}{P_0}$. We know $K = 10$ million, $P_0 = 2$ million, and $r = 0.032$\). Substituting these values, we get:\($A = \frac{10-2}{2} = 4$\)
Therefore, the equation for the population of the island is:\($P(t) = \frac{10}{1 + 4 e^{-0.032t}}$\)
To find the population in 2050, we substitute\($t = 100$\) (since 63 years have already passed and we want to find the population in 2050, which is 100 years after 1950):
\($P(100) = \frac{10}{1 + 4 e^{-0.032 \times 100}} \approx \boxed{8.76}$ million\)
Therefore, the estimated population of the island in 2050, assuming constant carrying capacity and consumption per capita, is approximately 8.76 million.
To know more about equation visit:
https://brainly.com/question/29657983
#SPJ11
In ΔSTU, s = 3.4 cm, ∠T=165° and ∠U=13°. Find the length of t, to the nearest 10th of a centimeter.
Answers
Answer:
25.2 cm
Step-by-step explanation:
\(\angle S=180^{\circ}-165^{\circ}-13^{\circ}=2^{\circ} \\ \\ \frac{t}{\sin T}=\frac{s}{\sin S} \\ \\ \frac{t}{\sin 165^{\circ}}=\frac{3.4}{\sin 2^{\circ}} \\ \\ t=\frac{3.4\sin 165^{\circ}}{\sin 2^{\circ}} \\ \\ t \approx 25.2\)
6x+44According to the model above, 4(6x + 4)Submit A
Answers
4(6x + 4) =
= 4(6x) + 4(4) =
= 24x + 16
Using the model:
| 6x | +4
4 | 24x | +16
What is 3 1/4 in cups as a whole number or mixed number in simplest form?
Answers
Answer:
3/4 = 34 = 0.75.
Step-by-step explanation:
Please help me step by step how to solve this quadratic equation 2a^2=-6+8a
Answers
The quadratic equation 2a^2 = -6 + 8a has two solutions: a = 3 and a = 1.
To solve the quadratic equation 2a^2 = -6 + 8a, we need to rearrange it into standard quadratic form, which is ax^2 + bx + c = 0, where a, b, and c are coefficients.
Step 1: Move all the terms to one side of the equation to set it equal to zero:
2a^2 - 8a + 6 = 0
Step 2: The equation is now in standard quadratic form, so we can apply the quadratic formula to find the solutions for 'a':
a = (-b ± √(b^2 - 4ac))/(2a)
Comparing with our equation, we have:
a = (-(-8) ± √((-8)^2 - 4(2)(6)))/(2(2))
Simplifying further:
a = (8 ± √(64 - 48))/(4)
a = (8 ± √16)/(4)
a = (8 ± 4)/(4)
Now, we can calculate the two possible solutions:
a1 = (8 + 4)/(4) = 12/4 = 3
a2 = (8 - 4)/(4) = 4/4 = 1
Therefore, the quadratic equation 2a^2 = -6 + 8a has two solutions: a = 3 and a = 1.
For more question on quadratic visit:
https://brainly.com/question/1214333
#SPJ8
solve
2r - 22 = 4(r-3)
Answers
Answer:r= -5
Step-by-step explanation:
Answer:
r=-5
Step-by-step explanation:
2r-22=4(r-3)
first expand brackets
2r-22=4r-12
then take away the least amount of r's from one side
-22=2r-12
add 12 to each side
-10=2r
divide by 2 to get r by itself
-5=r
Can anyone please solve this quadratic equation
X=-1/2( y-2)2 +3
Find axis of symmetry
Focus
Directrix
Vertex
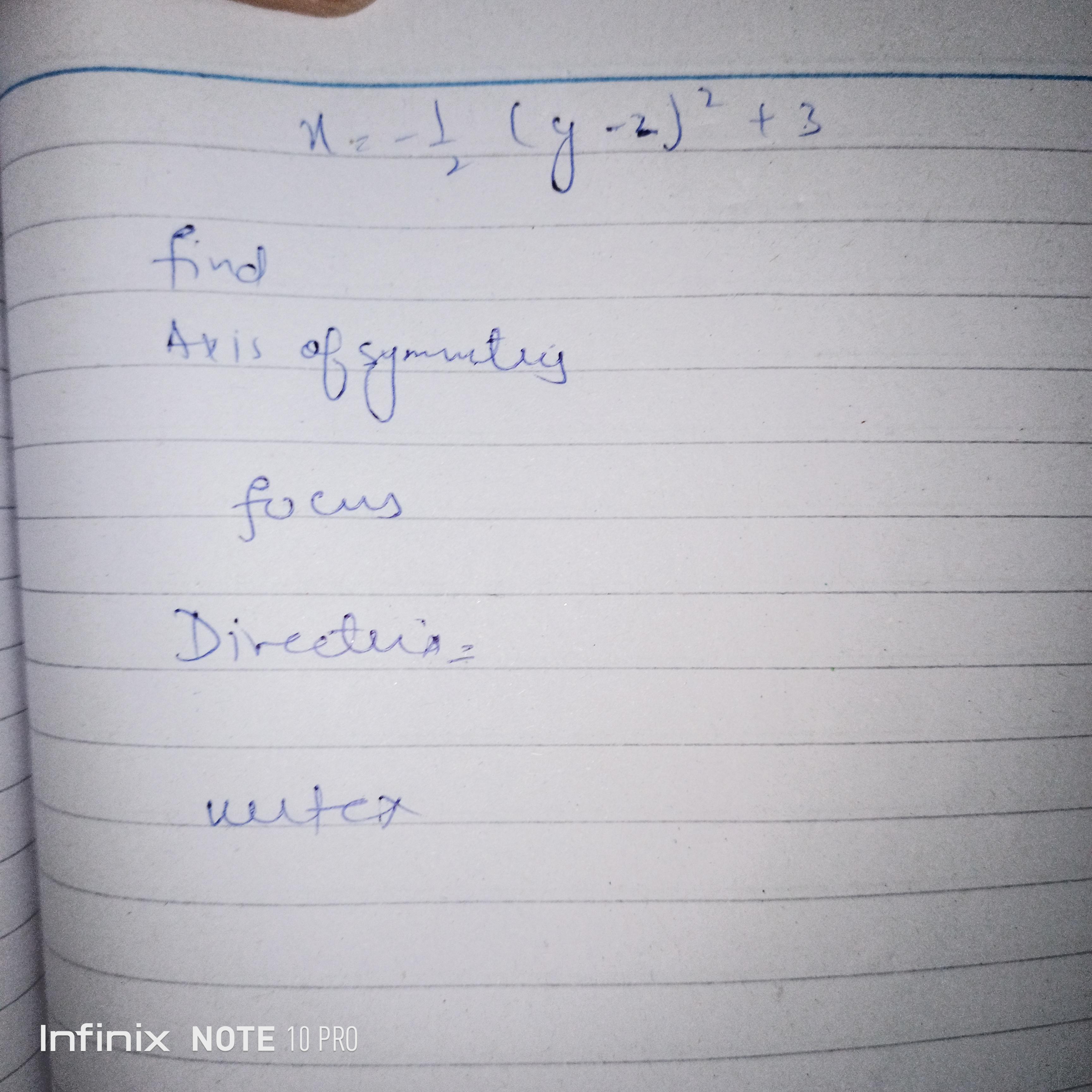
Answers
Answer:
could this be it
Step-by-step explanation:

find the first and second derivatives of the function x^4-3x^3 16x
Answers
The first derivative of the function f(x) = x^4 - 3x^3 + 16x is f'(x) = 4x^3 - 9x^2 + 16. The second derivative is f''(x) = 12x^2 - 18x.
To find the first derivative of the given function f(x) = x^4 - 3x^3 + 16x, we apply the power rule for differentiation. Each term of the function is differentiated separately. For the first term, x^4, the power rule states that the derivative is obtained by multiplying the coefficient (4) by the variable raised to one less power (4-1=3), resulting in 4x^3.
Similarly, for the second term, -3x^3, the derivative is -9x^2 obtained by multiplying the coefficient (-3) by the variable raised to one less power (3-1=2). Finally, the derivative of the last term, 16x, is simply 16, as the derivative of a constant term is zero. Combining these derivatives, we get f'(x) = 4x^3 - 9x^2 + 16.
To find the second derivative, we differentiate the first derivative, f'(x), using the same rules. For the first term, 4x^3, the power rule gives us 12x^2. For the second term, -9x^2, the derivative is -18x. Since the last term, 16, is a constant, its derivative is zero. Therefore, the second derivative is f''(x) = 12x^2 - 18x.
Learn more about derivative here:
https://brainly.com/question/29020856
#SPJ11
what is 4.0 x 10 by the 2nd power
Answers
Have a wonderful day
problem solving/data analysis additional topics in math heart of algebra passport to advanced mathematics
Answers
Problem Solving and Data Analysis, Heart of Algebra, and Passport to Advanced Mathematics are three additional topics in math that are part of the SAT Math section. These topics cover various concepts and skills that are essential for solving complex mathematical problems and analyzing data effectively.
Problem Solving and Data Analysis: This topic focuses on the ability to interpret and analyze real-world scenarios, solve problems using quantitative reasoning, and apply mathematical models to data. It includes concepts such as ratios, proportions, percentages, statistics, data interpretation, and data representation.
Heart of Algebra: This topic emphasizes algebraic concepts and skills, particularly those related to linear equations, linear inequalities, and systems of linear equations. It involves understanding and solving equations, manipulating algebraic expressions, graphing linear functions, and solving word problems using algebraic methods.
Passport to Advanced Mathematics: This topic builds upon the foundational algebraic skills and extends into more advanced mathematical concepts. It covers topics such as quadratic equations, exponential and logarithmic functions, radicals and rational exponents, polynomial operations, and complex numbers. It also involves solving higher-order equations, understanding function transformations, and applying algebraic concepts in various contexts.
These topics are important for SAT Math because they assess a student's ability to apply mathematical knowledge and problem-solving strategies to real-world situations. Familiarity with these topics enables students to analyze data, reason quantitatively, solve complex algebraic problems, and make connections between different mathematical concepts.
In conclusion, Problem Solving and Data Analysis, Heart of Algebra, and Passport to Advanced Mathematics are key topics in the SAT Math section. Mastering these topics is essential for achieving a high score on the SAT and for developing strong problem-solving and data analysis skills in mathematics.
To know more about Mathematics, visit
https://brainly.com/question/15209879
#SPJ11
FREE BRAINLIEST IF CORRECT: Write the following without the absolute value sign: |a^2| if a>0
Answers
Answer:
Step-by-step explanation:
When you square a number, whether it's positive or negative, the square is always positive. That is, a2 is positive whether a is positive or negative. Examples:
12 = 1 x 1 = 1
(-1)2 = (-1) x (-1) = 1
52 = 5 x 5 = 25
(-5)2 = (-5) x (-5) = 25
Since the answer is always positive, you don't need the absolute value signs: |a2| = a2.
hope this helps can i get brainly pls
Which of the following statements are correct?
Select only those statements you know to be correct because negative marking is applied within this question (although it is not possible to get a negative mark for the question overall).
a.
Cost machines and cost related to machining are considered to be part of inventory
b.
Ordering costs decrease with respect to lot size
c.
It is good to have fixed interval ordering systems for products that have independent demand
d.
Companies using ABC approach need not use EOQ
e.
Taxes and insurance costs can be considered as carrying costs of inventory
f.
Costs incurred for defective products identified after the products are shipped are classified as internal failure costs
g.
Costs spent to prevent low quality goods in production are classified as cost of reengineering
h.
Costs of repairing faulty products under warranty are limited to external failure costs
i.
Returned goods cannot be classified under internal failure costs
j.
Under EOQ inventory model there is an assumption which states that there is no possibility of inventory stockout to occur
Answers
The correct statements are:
b) Ordering costs decrease with respect to lot size,
c) It is good to have fixed interval ordering systems for products that have independent demand,
e) Taxes and insurance costs can be considered as carrying costs of inventory,
f) Costs incurred for defective products identified after the products are shipped are classified as internal failure costs,
h) Costs of repairing faulty products under warranty are limited to external failure costs, and j) Under EOQ inventory model, there is an assumption which states that there is no possibility of inventory stockout to occur.
b) Ordering costs decrease with respect to lot size: Ordering costs involve the expenses incurred when placing orders for inventory, such as administrative costs, processing fees, and transportation costs.
When the lot size increases, the frequency of placing orders decreases, resulting in lower ordering costs per unit. This is because the fixed costs associated with ordering are spread over a larger quantity of inventory.
c) It is good to have fixed interval ordering systems for products that have independent demand: Fixed interval ordering systems involve placing orders at regular intervals, regardless of the inventory level.
This approach is suitable for products with independent demand, where the demand is unpredictable or sporadic. By setting fixed intervals, the company can ensure a consistent replenishment schedule and avoid stockouts while optimizing inventory levels.
e) Taxes and insurance costs can be considered as carrying costs of inventory: Carrying costs are the expenses associated with holding and storing inventory.
They include costs such as storage fees, insurance premiums, taxes on inventory, and the opportunity cost of tying up capital in inventory. Taxes and insurance costs directly impact the financial burden of inventory holding and are considered as components of carrying costs.
f) Costs incurred for defective products identified after the products are shipped are classified as internal failure costs: Internal failure costs are expenses incurred due to quality issues discovered within the company's operations.
In the context of inventory, costs related to defective products identified after they are shipped, but before reaching the customer, fall under internal failure costs. These costs include rework, scrap, and any necessary corrective actions taken to address the quality problems.
h) Costs of repairing faulty products under warranty are limited to external failure costs: External failure costs are the expenses incurred due to quality issues discovered by customers after the products have been delivered.
When faulty products are repaired under warranty, the costs associated with the repairs are considered external failure costs. This includes the direct costs of repairing or replacing the faulty products and any associated customer service expenses.
j) Under EOQ inventory model, there is an assumption which states that there is no possibility of inventory stockout to occur: The Economic Order Quantity (EOQ) model is a widely used inventory management technique.
It assumes that demand for the product is constant and known with certainty, there are no quantity discounts or price variations, and there is no possibility of stockouts occurring.
The assumption of no stockouts simplifies the calculations and ensures that the optimal order quantity obtained from the model will meet the demand without interruptions.
However, in real-world scenarios, stockouts can occur due to unforeseen factors, variability in demand, or supply chain disruptions.
To know more about costs refer here:
https://brainly.com/question/17120857
#SPJ11
If y varies directly as x and x=3 when y=12, find x when y=3
Answers
Answer:
Answer:
y = 4x
Step-by-step explanation:
Given that x and y vary directly then the equation relating them is
y = kx ← k is the constant of variation
To find k use the condition x = 3 when y = 12
k = = = 4
y = 4x ← equation of variation
Practice working with interior angles of a triangle. Manipulate the triangle so angle A measures 14° and angle B measures 62°. Which statement is true about angle C? The angle is acute. The angle does not make a straight line with the other two. The angle is obtuse. The angle is a right angle.
Answers
Answer:
Its C
Step-by-step explanation:
Because i tried B and it didnt work
Lord, please help this is overdue and I need it by today

Answers
Answer:
-7.3 = -7.3
Step-by-step explanation:
-2.2+(-3.7 + (-1.4)) = -7.3 || -2.2+(-3.7 + (-1.4)) = -7.3
So it will be -7.3=-7.3
????? help out ( not good with math )

Answers
Answer:
The answer is x = 3
Step-by-step explanation:
5x + 9 = 24
5x +9 -9 = 24 - 9
5x = 15
x = 15/5 = 3
Therefore, x = 3
Kelly multiplied 5 to each side when she solved for x, which is incorrect.
Answer:
Kelly had incorrectly solved for \(x\) where she had multiplied by \(5\) instead of dividing by \(5\) to find for \(x\).
Step-by-step explanation:
How Kelly should have solved it:
\(5x+9 = 24\)
\(5x + 9-9= 24-9\)
\(5x=15\)
\(5x\div 5=15\div 5\) (mistake occurred during this step in Kelly's work where she had multiplied by \(5\))
\(x=3\)
Checking:
To check if \(x=3\), we can use substitution:
\(5x+9 = 5(3)+9\)
\(=15+9\)
\(=24\)
∴ The solution for \(x\) is correct.
Hope this helps :)
The exam scores for 200 students are normally distributed with a mean of 72 and a standard deviation of 10. Which answer choice below represents the number of students with scores between 72 and 82?.
Answers
Using the normal distribution, it is found that there are 68 students with scores between 72 and 82.
Normal Probability DistributionThe z-score of a measure X of a normally distributed variable with mean \(\mu\) and standard deviation \(\sigma\) is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score measures how many standard deviations the measure is above or below the mean. Looking at the z-score table, the p-value associated with this z-score is found, which is the percentile of X.In this problem, the mean and the standard deviation are given, respectively, by:
\(\mu = 72, \sigma = 10\)
The proportion of students with scores between 72 and 82 is the p-value of Z when X = 82 subtracted by the p-value of Z when X = 72.
X = 82:
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{82 - 72}{10}\)
Z = 1
Z = 1 has a p-value of 0.84.
X = 72:
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{72 - 72}{10}\)
Z = 0
Z = 0 has a p-value of 0.5.
0.84 - 0.5 = 0.34.
Out of 200 students, the number is given by:
0.34 x 200 = 68 students with scores between 72 and 82.
More can be learned about the normal distribution at https://brainly.com/question/24663213
#SPJ1
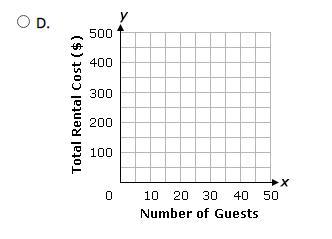
The cost of renting a community center is $100, with an additional cost of $10 per guest.
Which graph has the most appropriate scales and units for this situation?

Answers
Answer:
D
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
The number of guests is the independent variable and should be between 1 and 50. We can use a scale of 10's
The cost is the dependent variable and the minimum cost is 100 and should rise from there
The scale would be from 100 's
A number of squares are connected in a row to form a rectangle. The table shows the relationship between the number of squares, x, and the
perimeter, y, of the rectangles they form
Select all the true statements about this relation.

Answers
Answer:
✅The table can be represented by the equation, \( y = 4x + 4 \)
✅The relation is a function.
✅The graph of the function is linear.
Step-by-step explanation:
✍️The first statement: The table can be represented by the equation, \( y = 4x + 4 \).
To check if the first statement is correct let's find the equation that can represent the table by finding the slope (m) and y-intercept (b).
Using two pairs, (1, 8) and (2, 12),
Slope = \( \frac{y_2 - y_1}{x_2 - x_1} = \frac{12 - 8}{2 - 1} = \frac{4}{1} = 4 \).
Substitute, x = 1, y = 8, and m = 4 into y = mx + b to solve for b.
Thus:
8 = (4)(1) + b
8 = 4 + b
Subtract 4 from each side
8 - 4 = b
4 = b
Plug in the values of b and m into y = mx + b.
Thus, the equation that represents the table would be:
\( y = 4x + 4 \).
✅Therefore, the first statement is correct.
✍️The second statement: The graph of the function is non-linear.
This is NOT TRUE because the equation of the function, \( y = 4x + 4 \), represents the equation of a linear graph in the slope-intercept form. When graphed, it will give us a straight line.
✍️The Third statement: The relation is a function.
This is TRUE because each input value (x-value) has exactly one output value (y-value).
✍️The Fourth statement: The rate of change is NOT constant.
This standby is NOT TRUE.
The rate of change is the slope (m) that we have calculated above to be 4. Between any two pairs, the rate of change remains 4.
Therefore, this statement is not correct.
✍️The Fifth statement: The graph of the function is linear.
This is TRUE. As stated earlier, from the equation generated, it is safe to say that the equation represents graph of a linear function. The graph will be a straight line graph.
The true statements are:
(a) The equation of the function is \(\mathbf{y = 4x +4}\)(c) The relation is a function(e) The graph is linear(a) The equation of the function
Start by calculating the slope (m)
\(\mathbf{m = \frac{y_2 - y_1}{x_2 -x_1}}\)
So, we have:
\(\mathbf{m = \frac{12 - 8}{2 -1}}\)
\(\mathbf{m = 4}\)
The equation is then calculated as:
\(\mathbf{y = m(x -x_1) + y_1}\)
So, we have:
\(\mathbf{y = 4(x -1) + 8}\)
\(\mathbf{y = 4x -4 + 8}\)
\(\mathbf{y = 4x +4}\)
Hence, this statement is true
(b) The graph is nonlinear
Because of (a) above, the graph is linear
Hence, this statement is false
(c) The relation is a function
A linear relation is a function
Hence, this statement is true
(d) The rate of change is not constant
Because of (a) above, the rate of change is constant
Hence, this statement is false
(e) The graph is linear
Because of (a) above, the graph is linear
Hence, this statement is true
Read more about linear relations at:
https://brainly.com/question/7988877
what is 15t+8t-2t=16?
find the vaule of t
Answers
Answer:
Step-by-step explanation:
15t+8t-2t=16
23t - 2t = 16
21t = 16
t= 16/21
t≈0,762
A paper company needs to ship paper to a large printing business. The paper will be
shipped in small boxes and large boxes. The volume of each small box is 6 cubic feet
and the volume of each large box is 13 cubic feet. A total of 19 boxes of paper were
shipped with a combined volume of 156 cubic feet. Determine the number of small
boxes shipped and the number of large boxes shipped.
There were
Submit Answer
small boxes shipped and
large boxes shipped.

Answers
There were 13 small boxes shipped and 6 large boxes shipped.
Let's denote the number of small boxes as 's' and the number of large boxes as 'l'.
According to the given information, the volume of each small box is 6 cubic feet, so the total volume of all small boxes can be calculated as 6s cubic feet.
Similarly, the volume of each large box is 13 cubic feet, so the total volume of all large boxes can be calculated as 13l cubic feet.
We are also given that the combined volume of all the boxes is 156 cubic feet, so we can write the equation:
6s + 13l = 156 ...(1)
Additionally, we know that a total of 19 boxes were shipped, so we can write another equation:
s + l = 19 ...(2)
Now, we have a system of equations (equation 1 and equation 2) that we can solve simultaneously to find the values of 's' and 'l'.
To solve this system of equations, we can use substitution or elimination method. Let's use the substitution method here.
From equation 2, we can rewrite it as s = 19 - l.
Substituting this value of s into equation 1, we get:
6(19 - l) + 13l = 156
Simplifying the equation:
114 - 6l + 13l = 156
Combining like terms:
7l = 42
Dividing both sides by 7:
l = 6
Now, we can substitute this value of l back into equation 2 to find the value of s:
s + 6 = 19
s = 13
The number of small boxes shipped is 13, and the number of large boxes shipped is 6.
There were 13 small boxes shipped and 6 large boxes shipped.
For more questions on shipped
https://brainly.com/question/29352184
#SPJ8
The rectangular floor of a classroom is 38 feet in length and 26 feet in width. A scale drawing of the floor has a length of 19 inches. What is the area, in square inches, of the floor in the scale drawing?
Answers
Answer:
length is 19 width is 15
Step-by-step explanation:
The area of the classroom floor in the scale drawing is 247 square inches.
What is Area of Rectangle?The area of Rectangle is length times of width.
We need to find the scale of the drawing, which is the ratio of the length in the drawing to the actual length:
19 inches / 38 feet = 0.5 inches/foot
Now we can use the scale to find the dimensions of the classroom floor in the scale drawing:
Length in scale drawing = Actual length × Scale
Width in scale drawing = Actual width × Scale
Length in scale drawing = 38 feet × 0.5 inches/foot = 19 inches
Width in scale drawing = 26 feet × 0.5 inches/foot = 13 inches
So the dimensions of the classroom floor in the scale drawing are 19 inches by 13 inches.
To find the area in square inches, we can multiply the length by the width:
Area in scale drawing = Length in scale drawing × Width in scale drawing
= 19 inches× 13 inches
= 247 square inches
Therefore, the area of the classroom floor in the scale drawing is 247 square inches.
To learn more on Rectangle click:
https://brainly.com/question/20693059
#SPJ2
if two cards are chosen in a standard 52 card deck without replacement what is the probability that one of the cards is a heart and the other is a spades
Answers
When two cards are selected from a standard deck of 52 cards without replacement, the probability that one is a heart and the other is a spade can be calculated using the following steps:
Step 1: Determine the probability of selecting a heart card. There are 13 heart cards in a standard deck of 52 cards. Thus, the probability of selecting a heart card on the first draw is 13/52.
Step 2: Determine the probability of selecting a spade card. After one card has been selected and removed from the deck, there are 51 cards left in the deck. Among these cards, there are 13 spades cards. Therefore, the probability of selecting a spade card on the second draw is 13/51.
Step 3: Determine the probability of selecting a heart card and a spade card. The probability of selecting a heart card on the first draw and a spade card on the second draw is the product of the probabilities calculated in Step 1 and Step 2, respectively: P(heart and spade) = P(heart) × P(spade) = (13/52) × (13/51) = 169/2652 = 0.0637.
Step 4: Determine the probability of selecting a spade card and a heart card. The probability of selecting a spade card on the first draw and a heart card on the second draw is the same as the probability of selecting a heart card on the first draw and a spade card on the second draw. Therefore: P(spade and heart) = P(heart and spade) = 0.0637.
Step 5: Determine the total probability. The total probability of selecting one heart card and one spade card, regardless of the order in which they are selected, is the sum of the probabilities calculated in Steps 3 and 4:P(one heart and one spade) = P(heart and spade) + P(spade and heart) = 0.0637 + 0.0637 = 0.1274.
Thus, the probability that one of the cards is a heart and the other is a spade is 0.1274 or 12.74%.
Let's learn more about probability:
https://brainly.com/question/25870256
#SPJ11
a group of classmates surveyed how other students travel to school the results of the survey are shown in the table at right make a circle graph showing the results of the survey using percents, bus- 90, ride bike- 30, ride in car- 75, walk- 45.
Answers
So, on solving the provided question, we can say that equation of diagonal WY is 13.03 units
What is equation?An equation is a mathematical formula that connects two assertions using the equal sign (=) to denote equivalence. In algebra, an equation is a mathematical statement that establishes the equivalence of two mathematical expressions. For instance, an equal sign separates the components 3x + 5 and 14 in the equation 3x + 5 = 14. A mathematical formula is used to explain the connection between two sentences on either side of a letter. Frequently, there is just one variable, which is also the symbol. for example, 2x - 4 = 2.
by d=√((x2 – x1)² + (y2 – y1)²).
Coordinates of W = (-4,5) and Y = (3,-6)
= √((3 – (-4))² + (-6 – 5)²)
= √170
= 13.03 units
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
Consider the function ƒ : Rª → R³ given by = (1 + x + sin(z − 2y), e³z-w, 2z+tan(w+x²)). (b) Now consider the function g: R³ → R² given by f(x, y, z, w) = (a) Find the quadratic approximation of f at the point P = (0, 0, 0, 0). Use this approximation to estimate the value f(0.1, -0.1, -0.1, 0.1). g(x, y, z) = (sin(x - y), y cos(x² - z² – 1)). We can compose the maps f and g to obtain a smooth function g of: R4 → R². Use the chain rule to compute Dp (gof), where P = (0, 0, 0, 0)
Answers
To find the quadratic approximation of the function f at the point P = (0, 0, 0, 0), we need to compute the partial derivatives of f with respect to each variable at the point P.
The partial derivatives of f are as follows:
∂ƒ/∂x = 1 + 2x
∂ƒ/∂y = -2cos(z - 2y)
∂ƒ/∂z = cos(z - 2y)
∂ƒ/∂w = -e³w
∂²ƒ/∂x² = 2
∂²ƒ/∂y² = 4sin(z - 2y)
∂²ƒ/∂z² = -sin(z - 2y)
∂²ƒ/∂w² = -3e³w
Using these partial derivatives, we can construct the quadratic approximation of f at P:
Q(x, y, z, w) = f(0, 0, 0, 0) + ∂ƒ/∂x(0, 0, 0, 0)x + ∂ƒ/∂y(0, 0, 0, 0)y + ∂ƒ/∂z(0, 0, 0, 0)z + ∂ƒ/∂w(0, 0, 0, 0)w + (1/2)∂²ƒ/∂x²(0, 0, 0, 0)x² + (1/2)∂²ƒ/∂y²(0, 0, 0, 0)y² + (1/2)∂²ƒ/∂z²(0, 0, 0, 0)z² + (1/2)∂²ƒ/∂w²(0, 0, 0, 0)w²
Substituting the values:
Q(x, y, z, w) = 1 + 0 + 0 + 0 + 0 + (1/2)(2)x² + (1/2)(4sin(0))y² + (1/2)(-sin(0))z² + (1/2)(-3e³(0))w²
Q(x, y, z, w) = 1 + x²
Now we can estimate the value of f(0.1, -0.1, -0.1, 0.1) using the quadratic approximation:
f(0.1, -0.1, -0.1, 0.1) ≈ Q(0.1, -0.1, -0.1, 0.1) = 1 + (0.1)² = 1 + 0.01 = 1.01
Therefore, the estimated value of f(0.1, -0.1, -0.1, 0.1) using the quadratic approximation is approximately 1.01.
Now, let's compute Dₚ(g∘ƒ), where P = (0, 0, 0, 0), using the chain rule.
Dₚ(g∘ƒ) = Dₚg ∘ Dₚƒ
First, let's compute Dₚƒ:
Dₚƒ = (∂ƒ/∂x, ∂ƒ/∂y, ∂ƒ/∂z, ∂ƒ/∂w) at P
Dₚƒ = (1 + 2(0), -2cos(0 - 2(0)), cos(0 - 2(0)), -e³(0))
Dₚƒ = (1, -2, 1, -1)
Next, let's compute Dₚg:
Dₚg = (∂g₁/∂x, ∂g₁/∂y, ∂g₁/∂z, ∂g₁/∂w, ∂g₂/∂x, ∂g₂/∂y, ∂g₂/∂z, ∂g₂/∂w) at P
Dₚg = (cos(0 - 0), 0, 0, 0, 0, 0, 0, 0)
Dₚg = (1, 0, 0, 0, 0, 0, 0, 0)
Finally, we can compute Dₚ(g∘ƒ) by taking the composition of Dₚg and Dₚƒ:
Dₚ(g∘ƒ) = Dₚg ∘ Dₚƒ
Dₚ(g∘ƒ) = (1, 0, 0, 0, 0, 0, 0, 0) ∘ (1, -2, 1, -1)
Dₚ(g∘ƒ) = (1, 0, 0, 0, 0, 0, 0, 0)
Therefore, Dₚ(g∘ƒ) = (1, 0, 0, 0, 0, 0, 0, 0) at P = (0, 0, 0, 0).
To know more about partial derivatives refer here:
https://brainly.com/question/28751547#
#SPJ11
7th grade math help me please :)

Answers
Answer:
105 pounds
Step-by-step explanation: