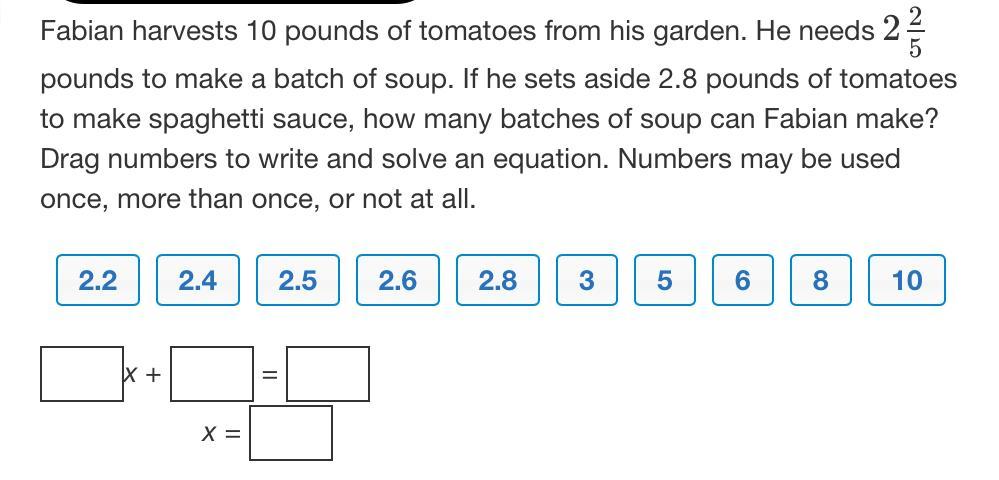
Answers
2.4x + 2.8 = 10
2.4x(2.4 is the cost to make x amount of soup)
+2.8 the amount used for sauce
=10 the total of the two
Related Questions
Locate the discontinuities of the function. (Use n where appropriate if there are infinitely many discontinuities.)
y = ln(tan^2x)
x=________
Answers
To locate the discontinuities of the function y = ln(tan^2x), we need to find the values of x where the function is not continuous.
First, let's consider the domain of the natural logarithm, ln(x). It is defined only for positive values of x, so tan^2x must be greater than 0 for the function to be defined.
Next, let's consider the domain of tan(x). Tan(x) is undefined when its denominator, cos(x), is equal to 0. This occurs at x = (2n + 1)π/2, where n is an integer.
Since we have tan^2x, the square of tan(x) will always be non-negative. However, we need it to be positive (greater than 0) for ln(tan^2x) to be defined. Tan^2x will be equal to 0 when tan(x) is 0, which occurs at x = nπ, where n is an integer.
Thus, the discontinuities of the function y = ln(tan^2x) occur at two different sets of x values:
1. x = (2n + 1)π/2, where n is an integer, due to the undefined nature of tan(x).
2. x = nπ, where n is an integer, due to tan^2x being 0, which is not in the domain of ln(x).
There are infinitely many discontinuities because of the variable n.
Learn more about function here:
https://brainly.com/question/12431044
#SPJ11
The data set shows the numbers of hours students volunteer for a community service project. Find and interpret the mean absolute deviation of the data. Write your answer as a decimal.
3, 3, 4, 4, 5, 6, 6, 6, 9, 10
Answers
Answer:
1.8
Step-by-step explanation:
1st step
To find the mean absolute deviation of the data, start by finding the mean of the data set.
2nd step
Find the sum of the data values, and divide the sum by the number of data values.
3rd step
Find the absolute value of the difference between each data value and the mean: |data value – mean|.
4th step
Find the sum of the absolute values of the differences.
5th step
Divide the sum of the absolute values of the differences by the number of data values.
Over the past several months, an adult patient has been treated for tetany (severe muscle spasms). This condition is associated with an average total calcium level below 6 mg/dl. Recently, the patient’s total calcium tests gave the following readings (in mg/dl).
9.3 8.8 10.1 8.9 9.4 9.8 10
9.9 11.2 12.1
Answers
Comparing the calculated average (9.85 mg/dl) to the average associated with tetany (below 6 mg/dl), we can see that the patient's average total calcium level is within the normal range. This suggests that the patient's tetany may not be caused by a deficiency in total calcium levels.
To analyze the patient's total calcium test readings and determine if they are within the normal range, we can calculate the average and compare it to the average associated with tetany (below 6 mg/dl).
The total calcium test readings are as follows:
9.3, 8.8, 10.1, 8.9, 9.4, 9.8, 10, 9.9, 11.2, 12.1
To calculate the average total calcium level, we sum up all the readings and divide by the number of readings:
Average = (9.3 + 8.8 + 10.1 + 8.9 + 9.4 + 9.8 + 10 + 9.9 + 11.2 + 12.1) / 10
Average = 98.5 / 10
Average = 9.85 mg/dl
Comparing the calculated average (9.85 mg/dl) to the average associated with tetany (below 6 mg/dl), we can see that the patient's average total calcium level is within the normal range. This suggests that the patient's tetany may not be caused by a deficiency in total calcium levels.
It's important to note that while the average total calcium level is within the normal range, individual readings may still vary. Further evaluation by a healthcare professional is necessary to determine the underlying cause of the patient's tetany.
Learn more about average from
https://brainly.com/question/130657
#SPJ11
A roll of wire 50 metres long is used to fence a rectangular plot of ground and to divide it into two plots by a fence joining the midpoints of the two opposite sides. What dimensions will maximize the total area enclosed?
Answers
The dimensions that will maximize the total area enclosed by the rectangular plot is; 12.5 m by 8.33 m
What dimension will maximize the area?
Let W represent the Width of the rectangular plot
Let L represent the Length with 3 pieces.
The total length will be 2W + 3L
The Area is L*W
Thus;
A = L*W
2W + 3L = 50
Solve for L
3L = 50 - 2W
L = (50 - 2W)/3
Put (50 - 2W)/3 for L in the Area equation to get;
A = ((50 - 2W)/3)*W
A = (50W - 2W²)/3
A = 50W/3 - 2W²/3
The maximum Area will occur at dA/dW = 0
dA/dW = 50/3 - 4W/3
At dA/dW = 0, we have;
50/3 - 4W/3 = 0
4W = 50
W = 50/4
W = 12.5 m
L = (50 - 2(12.5))/3
L = (50 - 25)/3
L = 25/3 = 8.33 m
Read more about Maximizing Area at; https://brainly.com/question/19819849
#SPJ1
please answer this !!!!

Answers
Answer:
7
Step-by-step explanation;
Rewriting our equation with parts separated:
4+1/7+2+6/7
Solving the whole number parts:
4+2=6
Solving the fraction parts:
1/7+6/7=7/7 (7/7 is a whole number) But first before simplifing, reduce the fraction, 7/7=1/1. Then 1/1=1.
Combining the whole and fraction parts:
(Solving the whole number parts - 6)
(Solving fraction parts - 1)
6+1 = 7plz help me
The monthly salary of a man increased from N2,700 to N3,200. Find the
percentage increase
A 10% . B 15% . C 15.6%. D 18.5%
Answers
Answer:
\(D\)
Step-by-step explanation:
\(2700*(1+x/100)=3200\)
\(1+x/100=3200/2700\)
\(1+x/100=32/27\)
\(x/100=32/27-1\)
\(x/100=5/27\)
\(27x=500\)
\(x=500/27\)
\(x=18.518518518518\)
Caculate the unit rate. Traveling 380 miles in 6
hours. How many miles per hour?
Answers
Answer: around 63.3
Step-by-step explanation: you need to find how much they traveled first (380) & then divided that by the other number (6). then you get somewhere around 63.3 . :))
Answer:
63.3
Step-by-step explanation:
The outcome is random if we know the possible values it can have, but not which particular value it takes
Answers
The outcome is random if we know the possible values it can have, but not which particular value it takes.
Is the outcome random if we know the possible values it can have?Randomness refers to the property of a process or system where the outcome is uncertain, unpredictable, and not predetermined. In a random process, we know the set of possible outcomes.
But we cannot determine which particular outcome will occur until it actually happens. For example, when flipping a fair coin, the possible outcomes are heads or tails.
But we do not know which one will come up until the coin is flipped. Randomness is a fundamental concept in probability theory and is used to model and analyze a wide range of phenomena.
Including games of chance, genetics, and quantum mechanics.
Learn more about outcome is random
brainly.com/question/31608092
#SPJ11
A community is building a new outdoor basketball court. The length of the court is twice the width.

Answers
Answer:
Step-by-step explanation:

The width of the basketball court is given by W(A) = √(A/2), and the length is given by L(A) = √(2A). These expressions allow you to calculate the width and length of the court for a given area A in square feet.
The problem states that the width of the basketball court (W) can be modeled by the equation:
W(A) = √(A/2)
where A is the area of the court in square feet.
Since the length (L) of the basketball court is twice the width (W), we can express it as:
L = 2W
Now, let's find the expression for the length (L) in terms of the area (A) of the court.
Step 1: Substitute the value of W from the given model into the expression for L:
L = 2 × √(A/2)
Step 2: Simplify the expression:
L = √(4A/2)
L = √(2A)
So, the expression for the length (L) of the basketball court in terms of its area (A) is given by L = √(2A).
To summarize, the width of the basketball court is given by W(A) = √(A/2), and the length is given by L(A) = √(2A). These expressions allow you to calculate the width and length of the court for a given area A in square feet.
To know more about width
https://brainly.com/question/15161439
#SPJ2
Complete question :- A community is building a new outdoor basketball court. The length of the court is twice the width. The width of the basketball court in feet can be modeled by w(A)= √A/2 where a is the area in square feet of the court.
In a standard deck of 52 cards, you are getting two cards. Find the probability of picking a king, and then another king.
Answers
Answer: P(King AND King) = 1/221
Step-by-step explanation:
There are 4 Kings in a deck of 52 cards total
Probability of getting a King first time:
P(King) = 4/52 > 4 Kings out of 52 total cards
P(King) = 1/13 >reduced fraction by dividing top and
bottom by 4
Probability of getting another king:
P(King) = 3/51 > You took out a king so there are 3 left and 1
less to the total making 51
P(king) = 1/17 >Reduced by dividing top and bottom by 3
Probability of getting king and then king again. The second king is dependent on you getting a king the first time. Because it is dependent, you multiply the 2 probabilities
P(King AND King) = (1/13)(1/17)
P(King AND King) = 1/221
The equation y = 2.391x +57.420 models the taste rating of a cereal, y, in a survey, where x is the number of grams of sugar per serving.
What does the y-intercept of the equation represent in context of the situation?
A cereal with 0 grams of sugar has a rating of about 57.
A cereal with 0 grams of sugar has a rating of about 2.391.
The average number of grams of sugar is 57.
The average number of grams of sugar is 2.
D
Answers
The y - intercept represents a cereal with zero grams of sugar that has a rating of about 57.
What is the general equation of a straight line?The general equation of a straight line is -
y = mx + c
where -
m → slope of line
c → y-intercept of line
Given a equation → y = 2.391x + 57.420 that models the taste rating of a cereal 'y' and 'x' represents the number of grams of sugar per serving.
The y-intercept of the equation represents the point at which the graph of the equation cuts the y - axis. Now, the coordinates of the y-intercept is of the form (0, y). Therefore, the x-coordinate will be 0. Now, the equation given is -
y = 2.391x + 57.420
Comparing it with the general equation of line -
y = 2.391x + 57.420
y = mx + c
The y - intercept is c = 57.420
At x = 0, the equation becomes -
y = 2.391 x 0 + 57.420
y = 57.420
Now -
Number of grams of sugar per serving = 0
Taste rating of a cereal = y = 57.420
Therefore, the y - intercept represents a cereal with zero grams of sugar that has a rating of about 57.
To solve more questions on Straight line modelling, visit the link below-
https://brainly.com/question/14992642
#SPJ1
Find y as a function of t if 8y″+28y=0, y(0)=3,y′(0)=4. y(t)=? Note: This particular weBWorK problem can't handle complex numbers, so write your answer in terms of sines and cosines, rather than using e to a complex power.
Answers
The y as a function of t if 8y″+28y=0, y(0)=3,y′(0)=4. then y(t) = (3√2 cos(2√2 t) + 2√2 sin(2√2 t))
To find the solution for the given second-order linear homogeneous differential equation, we can assume a solution of the form y(t) = e^(rt), where r is a constant to be determined. Plugging this into the equation, we get the characteristic equation:
8r^2 + 28 = 0
Simplifying the equation, we have:
r^2 = -28/8 = -7/2
Since the problem does not handle complex numbers, we express the solution in terms of sines and cosines instead of using e to a complex power. The complex roots of the equation are ±i√(7/2).
Using Euler's formula, we can write the complex roots in terms of sines and cosines:
r₁ = i√(7/2) = i√(7/2) = √(7/2) (cos(π/2) + i sin(π/2))
r₂ = -i√(7/2) = -√(7/2) (cos(π/2) + i sin(π/2))
The general solution of the differential equation is given by:
y(t) = c₁e^(√(7/2)t) cos(√(7/2)t) + c₂e^(√(7/2)t) sin(√(7/2)t)
To find the particular solution, we can substitute the initial conditions into the general solution:
y(0) = c₁ cos(0) + c₂ sin(0) = c₁ = 3
y'(0) = c₁(-√(7/2)) sin(0) + c₂(√(7/2)) cos(0) = c₂(√(7/2)) = 4
Solving the equations, we find c₁ = 3 and c₂ = 4/√(7/2) = 4√2/√7 = 4√2/√7 * (√7/√7) = 4√14/7.
Therefore, the solution to the differential equation is:
y(t) = 3 cos(√(7/2)t) + (4√14/7) sin(√(7/2)t)
Simplifying further:
y(t) = (3√2 cos(2√2 t) + 2√2 sin(2√2 t))
To learn more about differential equation click here
brainly.com/question/25731911
#SPJ11
Which of the following represents a rotation of △LMN, which has vertices L(4,5), M(0,2), and N(−2,−4), about the origin by 180°?
Answers
a)
L (−4, −5)
M (2, 4)
N (0, −2)
b)
L (−5, −4)
M (−2, 0)
N (4, 2)
c)
L (−4, −5)
M (0, −2)
N (2, 4)
Answers
Answer:
C
Step-by-step explanation:
Geometrically: if we set a circle at the point of origin and it's radius is one of the points (I used L), then we simple rotate the point 180 degrees around the circle and discover our new coordinate.
doing this for all three points yields C.
Answer:
L (−4, −5)
M (0, −2)
N (2, 4)
Step-by-step explanation:
The rule for this particular rotation is: (x, y)→(−x, −y).
To visualize why this is the case, the rotation can also be seen as the 180°clockwise rotation of the x- and y- axes about the origin while the figure remains in place. This rotation changes all x distances into x distances of the opposite sign, and all y distances into y distances of the opposite sign.
Apply the rule to each of the vertices of the triangle.
L(4, 5) → L'(−4, −5)
M (0, 2) → M' (0, −2)
N (−2, −4) → N' (2, 4)
Therefore, the coordinates of the vertices of the rotated triangle are
L' (−4, −5)
M' (0, −2)
N' (2, 4)
The temperatures of two cities were measured at the same time. The
temperature in city A was 60 degrees and rose at a constant rate of 2
degrees per hour.
The temperature in city B was 40 degrees and rose at a constant rate
of 10 degrees per hour.
Enter the number of hours it took for the temperature to be the same in
both cities.
Answers
Answer:
2.5 hours
Step-by-step explanation:
60+2t=40+10t
hope this helps, have a great day :)
Round 3,989.23655 to the nearest thousandth.
3,989.236
3,989.237
3,989.240
4,000
Answers
Answer:
3,989.240
Step-by-step explanation:
Answer:
3,989.240
Step-by-step explanation:
hope dis helps :/
While planning a vacation to Europe, Cal wanted to go to Dublin, Ireland, London, England and Paris, France. The distance from Dublin to London is 78 more miles than the distance between London and Paris. If the distance between Dublin and Paris is 504 miles, including the stop in London, what is the distance between London and Paris? What is the distance between Dublin and London?
Please show your work!
Answers
Answer:
291
Step-by-step explanation:
Think of a triangle with vertices D (Dublin), L (London), and P (Paris).
Let x = DL
Let y = LP
Let z = DP
"The distance from Dublin to London is 78 more miles than the distance between London and Paris."
DL = LP + 78
x = y + 78
If the distance between Dublin and Paris is 504 miles, including the stop in London.
DL + LP = 504
x + y = 504
x = y + 78
x + y = 504
y + 78 + y = 504
2y = 426
y = 213
x = y + 78
x = 213 + 78
x = 291
Answer:
The distance between London and Paris is 213 miles, and the distance between Dublin and London is 291 miles.
Step-by-step explanation:
Let's assign variables to the unknown distances:
Distance from London to Paris = x
Distance from Dublin to London = x + 78
According to the given information, the distance between Dublin and Paris, including the stop in London, is 504 miles. Using these values, we can set up the equation:
Distance from Dublin to London + Distance from London to Paris = 504
(x + 78) + x = 504
Combining like terms:
2x + 78 = 504
Subtracting 78 from both sides:
2x = 426
Dividing both sides by 2:
x = 213
Therefore, the distance between London and Paris is 213 miles, and the distance between Dublin and London is 213 + 78 = 291 miles.
A scale drawing for a restaurant is shown below.In the drawing, represents .Assuming the dining hall is rectangular, find the area of the real dining hall

Answers
Answer
Area of the real dining hall = 72 m²
Explanation
The area of any rectangular shape is given as
Area = L × W
where
L = Length of the rectangle
W = Width of the rectangle
For this question, we have been given the dimensions of the dining hall in the drawing and told that
5 cm in the drawing = 6 m in reality
So, if the real length of the dining is L
5 cm = 6 m
10 cm = L
We can write a mathematical relationship by cross multiplying
(5) (L) = (10) (6)
5L = 60
Divide both sides by 5
(5L/5) = (60/5)
L = 12 m
If the real width of the dining hall is W
5 cm = 6 m
5 cm = W
We can write a mathematical relationship by cross multiplying
(5) (W) = (5) (6)
5W = 30
Divide both sides by 5
(5W/5) = (30/5)
W = 6 m
So, for the real dining hall,
Length = 12 m
Width = 6 m
Area = Length × Width
Area = 12 × 6
Area = 72 m²
Hope this Helps!!!
repost, algebra help needed please
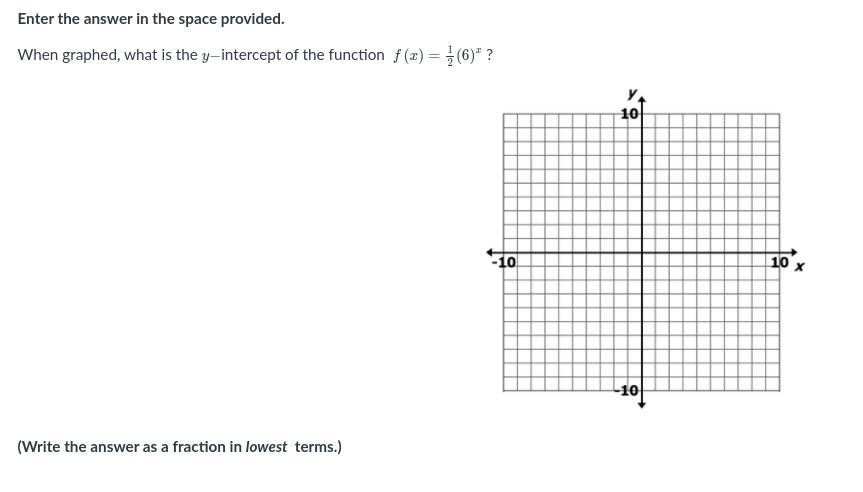
Answers
Answer:
y- intercept = \(\frac{1}{2}\)
Step-by-step explanation:
Given
f(x) = \(\frac{1}{2}\) \((6)^{x}\)
To find the y- intercept let x = 0 , then
f(0) = \(\frac{1}{2}\) \((6)^{0}\) [ \(6^{0}\) = 1 ]
= \(\frac{1}{2}\) × 1 = \(\frac{1}{2}\) ← y- intercept
the sum of two numbers is 121. if the larger number is 7 more than the smaller number, find both number.
Answers
Answer:
57 and 64
Step-by-step explanation:
x = smaller number
x + x + 7 = 121
2x = 114
x = 57
Find the solution to dạy +y= 1 = y(0) = 0 7(0) = 0 = = dt2 cos(t) Remember to explicitly represent multiplication by * and to use log for natural logarithm. y(t) = symbolic expression ?
Answers
The solution is:
y(t) = (1/2)×cos(t) - (1/2)tsin(t) + (1/2)×∫[0,t] sin(τ)×cos(τ)dτ
What is the variation of parameters?
A typical approach for finding a specific differential equation solution involves replacing the constants in the answer to a related (homogeneous) equation with functions and figuring out these functions in such a way that the original differential equation is satisfied.
Here, we have
Given: the differential equation d²y/dt² + y = cos(t) with initial conditions y(0) = 0 and y'(0) = 0 can be found using the method of Variation of Parameters.
Where the integral represents the convolution of the functions cos(t) and sin(t) with Green's function of the differential equation, which is sin(t).
The first two terms are the homogeneous solution of the differential equation, while the third term is the particular solution obtained using the method of Variation of Parameters.
To obtain this solution, we first find the homogeneous solution by assuming y(t) = Acos(t) + Bsin(t) and substituting it into the differential equation. We then solve for the constants A and B using the initial conditions.
Next, we use the method of Variation of Parameters to find the particular solution, which involves finding two functions u(t) and v(t), and using them to construct the particular solution.
Finally, we add the homogeneous and particular solutions to obtain the general solution to the differential equation.
Hence, y(t) = (1/2)×cos(t) - (1/2)tsin(t) + (1/2)×∫[0,t] sin(τ)×cos(τ)dτ
To learn more about the variation of parameters from the given link
https://brainly.com/question/30619063
#SPJ4
Solve the system of linear equations using
substitution. Y=x-3
Y=8x-31
Answers
Answer:
x=4 y=1 or (4,1)
Step-by-step explanation:
Plzzz giving brainilest no cap

Answers
Answer:
-0.6 yards
Step-by-step explanation:
The temperature at a point (x,y,z) is given by
T(x,y,z)=200e−ˣ²−⁵ʸ²−⁷ᶻ²
where T is measured in ∘C and x,y,z in meters
Find the rate of change of temperature at the point P(4,−1,4) in the direction towards the point (5,−4,5).
Answers
The rate of change of temperature at the point P(4,−1,4) in the direction towards the point (5,−4,5) is 0.
To find the rate of change of temperature at point P(4, -1, 4) in the direction towards the point (5, -4, 5), we need to calculate the gradient of the temperature function T(x, y, z) and then evaluate it at the given point.
The gradient of a function represents the rate of change of that function in different directions. In this case, we can calculate the gradient of T(x, y, z) as follows:
∇T(x, y, z) = (∂T/∂x) i + (∂T/∂y) j + (∂T/∂z) k
To calculate the partial derivatives, we differentiate each term of T(x, y, z) with respect to its respective variable:
∂T/∂x = 200e^(-x² - 5y² - 7z²) * (-2x)
∂T/∂y = 200e^(-x² - 5y² - 7z²) * (-10y)
∂T/∂z = 200e^(-x² - 5y² - 7z²) * (-14z)
Now we can substitute the coordinates of point P(4, -1, 4) into these partial derivatives:
∂T/∂x at P(4, -1, 4) = 200e^(-4² - 5(-1)² - 7(4)²) * (-2 * 4)
∂T/∂y at P(4, -1, 4) = 200e^(-4² - 5(-1)² - 7(4)²) * (-10 * -1)
∂T/∂z at P(4, -1, 4) = 200e^(-4² - 5(-1)² - 7(4)²) * (-14 * 4)
Simplifying these expressions gives us:
∂T/∂x at P(4, -1, 4) = -3200e^(-107)
∂T/∂y at P(4, -1, 4) = 2000e^(-107)
∂T/∂z at P(4, -1, 4) = -11200e^(-107)
Now, to find the rate of change of temperature at point P in the direction towards the point (5, -4, 5), we can use the direction vector from P to (5, -4, 5), which is:
v = (5 - 4)i + (-4 - (-1))j + (5 - 4)k
= i - 3j + k
The rate of change of temperature in the direction of vector v is given by the dot product of the gradient and the unit vector in the direction of v:
Rate of change = ∇T(x, y, z) · (v/|v|)
To calculate the dot product, we need to normalize the vector v:
|v| = √(1² + (-3)² + 1²)
= √(1 + 9 + 1)
= √11
Normalized vector v/|v| is given by:
v/|v| = (1/√11)i + (-3/√11)j + (1/√11)k
Finally, we can calculate the rate of change:
Rate of change = ∇T(x, y, z) · (v/|v|)
= (-3200e^(-107)) * (1/√11) + (2000e^(-107)) * (-3/√11) + (-11200e^(-107)) * (1/√11)
= 0
Since, the value of e^(-107) = 0.
Therefore, rate of change = 0.
To learn more about partial derivatives visit:
brainly.com/question/28750217
#SPJ11
If me and my brother pay for groceries and the total was 443 and I pay 243 and he pays 200 but we get paid back 75 each how much should I get paid
Answers
Find the general solution for the following differential equation using the method of undetermined coefficients d²y/dx - 36 y = cosh3x.
Answers
The general solution for the given differential equation is the sum of the complementary function and the particular solution:
\(y = y_h + y_p\\\\= C_1e^{6x} + C_2e^{-6x} + (-1/70)e^{3x} + (-1/70)e^{-3x}\)
where C₁ and C₂ are arbitrary constants determined by the initial or boundary conditions of the problem.
We are given the differential equation: d²y/dx - 36y = cosh(3x).
In this case, the homogeneous equation is d²y/dx - 36y = 0.
The characteristic equation associated with the homogeneous equation is obtained by replacing the derivatives with their corresponding algebraic expressions. In our case, we have r² - 36 = 0. Solving this quadratic equation, we find the roots to be r = ±6.
Since the roots are distinct and real, the general solution for the homogeneous equation is given by:
\(y_h = C_1e^{6x} + C_2e^{-6x}\)
where C₁ and C₂ are arbitrary constants determined by the initial or boundary conditions of the problem.
The term cosh(3x) can be written as a linear combination of exponential functions using the identities:
\(cosh(ax) = (e^{ax} + e^{-ax})/2, \\\\sinh(ax) = (e^{ax} - e^{-ax})/2.\)
Therefore, \(cosh(3x) = (e^{3x} + e^{-3x})/2.\)
Now, we assume the particular solution has the form:
\(y_p = A_1e^{3x} + A_2e^{-3x}\)
where A₁ and A₂ are undetermined coefficients.
Substituting these derivatives into the original differential equation, we get:
\((9A_1e^{3x} + 9A_2e^{-3x}) - 36(A_1e^{3x} + A_2e^{-3x}) = (e^{3x} + e^{-3x})/2.\)
To satisfy this equation, the coefficients of the exponential terms on both sides must be equal. Therefore, we have the following system of equations:
9A₁ - 36A₁ = 1/2,
9A₂ - 36A₂ = 1/2.
Solving these equations, we find A₁ = -1/70 and A₂ = -1/70.
Thus, the particular solution is:
\(y_p = (-1/70)e^{3x} + (-1/70)e^{-3x}\)
Finally, the general solution for the given differential equation is the sum of the complementary function and the particular solution:
\(y = y_h + y_p\\\\= C_1e^{6x} + C_2e^{-6x} + (-1/70)e^{3x} + (-1/70)e^{-3x}\)
where C₁ and C₂ are arbitrary constants determined by the initial or boundary conditions of the problem.
To know more about differential equation here
https://brainly.com/question/30074964
#SPJ4
The accompanying table shows the number of bacteria present in a certain culture
over a 5 hour period, where x is the time, in hours, and y is the number of bacteria.
Write an exponential regression equation for this set of data, rounding all coefficients
to the nearest thousandth. Using this equation, determine the number of bacteria
present after 10 hours, to the nearest whole number.
Hours (x) Bacteria (y)
0
1663
1
1821
2
2135
3
2467
4
2740
3179
10
5
Answers
The exponential regression equation for this set of data is y = \(14.129e^{(0.495x)\) and the number of bacteria present after 10 hours is approximately 24684.
The exponential regression equation for this set of data can use a calculator or spreadsheet software.
The equation will have the form y = abˣ a is the initial number of bacteria and b is the growth rate.
Using the given data can create a table of values for the equation:
x y ln(y)
---------------------------------------
0 16 2.773
1 66 4.189
2 311 5.739
3 791 6.672
4 1553 7.349
5 2571 7.853
A regression tool can find that the equation is approximately y = \(14.129e^{(0.495x)\) rounded to three decimal places.
The initial amount of bacteria is approximately a = 14.129 and the growth rate is approximately b = 1.649.
The number of bacteria present after 10 hours can plug x = 10 into the equation:
y = \(14.129e^{(0.495\times 10)\)
= 24683.522
Rounding to the nearest whole number get that the number of bacteria present after 10 hours is approximately 24684.
For similar questions on number of bacteria
https://brainly.com/question/23653869
#SPJ11
please help me on it

Answers
Answer:
36 m
Step-by-step explanation:
Pythagorean Theorem:
a² + b² = c²
27 = b
45 = c
So let's solve
a² + 27² = 45²
a² + 729 = 2025
a² = 1296
√1296 = a
= 36
units = m
36 units
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
when a survey questionnaire in english is translated into korean for use in south korea and then translated back into english to check its accuracy, it is described as:
Answers
When an English-language survey questionnaire is converted into a Korean version for usage in south Korea and then translated back into English to ensure accuracy.
Given statement;
When a survey questionnaire in English is translated into Korean for use in south Korea and then translated back into English to check its accuracy.
It can be described as back translation,
Back Translation:
Back translation, also known as reverse translation, is the process of literally translating text back into the source language from the target language. Translations from English to Swedish not affect would also include a reverse translation into English so that the meaning of the translated option could be clearly understood. Back translations have no effect on the translator's translation memory or other tools, such as glossaries.
It is described as a back translation.
To learn more about accuracy click here:
brainly.com/question/13099041
#SPJ4
In the figure below, find the exact value of y.

Answers
9514 1404 393
Answer:
2
Step-by-step explanation:
y is the geometric mean of the segment lengths.
y = √(4·1)
y = 2
_____
You can also get there by considering the similarity of the triangles:
short side / long side = y/4 = 1/y
y^2 = 4 . . . . . . . multiply by 4y\
y = √4 = 2 . . . . take the square root
Write the cubes of 5 natural numbers which are of the form 3n + 1 (eg.4,7,10…)and verify the following
"The cube of a natural number of the form 3n + 1 is a natural number of the
Same form
in when divided by 3 it leaves the remainder 1'
Answers
Answer:
yes it is true
Step-by-step explanation:
write the first five elements then write their cubes then write the cubes in the same form
for eg:
4³=16= 3×5+1= 3n+1
7³=49=3×16 +1= 3n + 1
and so on till the fifth element...