Answers
Area=54
Related Questions
1. Make Sense of the Task
2. Representing & Solving the Task
3. Accuracy
4. Communicating & Reasoning
5. Proof of work! You can redo it the same way OR even better, use a totally different method!!
Work Sample Question:
Farmer John has a rectangular holding pen that measures 10 yards long and
5 yards wide to contain his cattle. He is acquiring more cattle from the
neighboring farmer and wants to add the same amount of fencing to each
side to create a new holding pen that encloses 176 square yards. How
much should FarmerJohn add on to each side of his existing holding pen to
achieve his goal?

Answers
Answer:
each side to the fence has 6 units added to have an area of 176
Step-by-step explanation:
Let me know if you need anything more !!
Happy to help :)



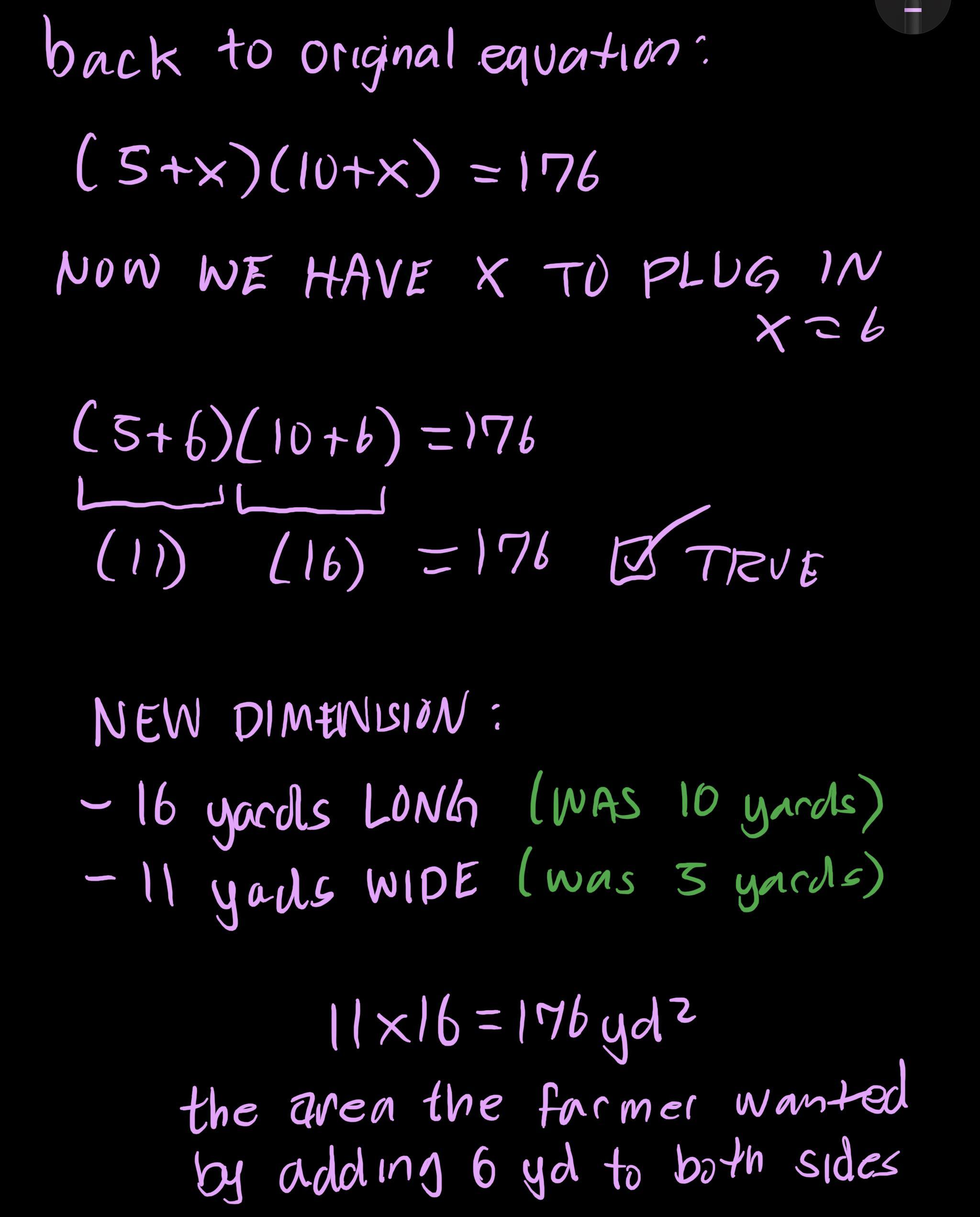

If you roll a 6-sided die 6 times, what is the best prediction possible for the number of times you will roll a three?
Answers
Answer: The best prediction possible for the number of times you roll a three is 1/6 of a roll.
Step-by-step explanation:
When you find the statistics of something like rolling a die, you will need to divide how many times you roll the die by how many sides are on the die.
6 - how many times you roll the die
6 - how many sides are on the die
When you divide 6 by 6, you will get one. Since both of the statistical numbers are the same, you will get an 1/6 chance of rolling a 1, 2, 3, 4, 5, and 6. So 1/6 is the answer! Hope this helps!!!
P.S (I learned this in 5th grade :))
WILL GIVE BRAINLIEST!!!! ANSWER ASAP!!!
Solve for x: 2|2x − 2| + 4 = 20. (5 points)
x = 5, x = −3
x = 5, x = −5
x = 3, x = −3
x = −5, x = 3
Answers
I plugged and checked and trust me the both work
Assessment
MULTIPLE CHOICE
Directions: Read and answer the questions carefully. Write th
your Mathematics notebook.
1. Which of the following is a well - defined set?
A. The set of big people.
B. The set of happy people.
C. The set of prime numbers.
D. The set of intelligent teachers.
Answers
Answer:
C. The set of prime numbers.
Thank you ☺️
Solve the following linear programming problem using the simplex method: Minimize: Z = X1 + 2X2 subject to
A. X1+3X2 ≥90
B. 8X1 +2X2 ≥ 160
C. 3X1 +2X2 ≥ 120
D. X2 ≤70
E. X1, X2 ≥ 0
Answers
The answer to the given linear programming problem, which is solved using the simplex method, is as follows:
The optimal solution to minimize the objective function Z = X1 + 2X2 is X1 = 20 and X2 = 0, with the objective function value Z = -100.
To solve the problem, we'll first convert the inequalities to equations by introducing slack and surplus variables. Then we'll set up the initial simplex tableau and iterate through the simplex algorithm until we reach an optimal solution.
⇒ Convert the inequalities to equations:
A. X1 + 3X2 + S1 = 90 (where S1 is the slack variable)
B. 8X1 + 2X2 + S2 = 160 (where S2 is the slack variable)
C. 3X1 + 2X2 + S3 = 120 (where S3 is the slack variable)
D. X2 + S4 = 70 (where S4 is the surplus variable)
⇒ Set up the initial simplex tableau:
| X1 | X2 | S1 | S2 | S3 | S4 | RHS |
----------------------------------------------
Z | -1 | -2 | 0 | 0 | 0 | 0 | 0 |
----------------------------------------------
S1 | 1 | 3 | 1 | 0 | 0 | 0 | 90 |
S2 | 8 | 2 | 0 | 1 | 0 | 0 | 160 |
S3 | 3 | 2 | 0 | 0 | 1 | 0 | 120 |
S4 | 0 | 1 | 0 | 0 | 0 | -1 | 70 |
⇒ a) Select the most negative coefficient in the Z row, which is -2. Choose the corresponding column as the pivot column (X2 column).
b) Find the pivot row by selecting the minimum ratio of the RHS value to the positive values in the pivot column. The minimum ratio is 70/1 = 70. Thus, the pivot row is S4.
c) Perform row operations to make the pivot element (1 in S4 row) equal to 1 and eliminate other elements in the pivot column:
- Divide the pivot row by the pivot element (1/1 = 1).
- Replace other elements in the pivot column using row operations:
- S1 row: S1 = S1 - (1 * S4) = 90 - 70 = 20
- Z row: Z = Z - (2 * S4) = 0 - 2 * 70 = -140
- S2 row: S2 = S2 - (0 * S4) = 160
- S3 row: S3 = S3 - (0 * S4) = 120
d) Update the tableau with the new values:
| X1 | X2 | S1 | S2 | S3 | S4 | RHS |
----------------------------------------------
Z | -1 | 0 | 0 | 0 | 2 | -2 | -140|
----------------------------------------------
S1 | 1 | 3 | 1 | 0 |
0 | 0 | 20 |
S2 | 8 | 2 | 0 | 1 | 0 | 0 | 160 |
S3 | 3 | 2 | 0 | 0 | 1 | 0 | 120 |
S4 | 0 | 1 | 0 | 0 | 0 | -1 | 70 |
e) Repeat steps a to d until all coefficients in the Z row are non-negative.
- Select the most negative coefficient in the Z row, which is -1. Choose the corresponding column as the pivot column (X1 column).
- Find the pivot row by selecting the minimum ratio of the RHS value to the positive values in the pivot column. The minimum ratio is 20/1 = 20. Thus, the pivot row is S1.
- Perform row operations to make the pivot element (1 in S1 row) equal to 1 and eliminate other elements in the pivot column.
- Update the tableau with the new values.
f) The final simplex tableau is:
| X1 | X2 | S1 | S2 | S3 | S4 | RHS |
----------------------------------------------
Z | 0 | 0 | 0 | 0 | 1 | -3 | -100|
----------------------------------------------
X1 | 1 | 3 | 1 | 0 | 0 | 0 | 20 |
S2 | 0 | -22 | -8 | 1 | 0 | 0 | 140 |
S3 | 0 | -7 | -3 | 0 | 1 | 0 | 60 |
S4 | 0 | 1 | 0 | 0 | 0 | -1 | 70 |
⇒ Read the solution from the final tableau:
The optimal solution is X1 = 20 and X2 = 0, with the objective function value Z = -100.
To know more about the simplex method, refer here:
https://brainly.com/question/30387091#
#SPJ11
what is the perimeter of a rectangle with length of 15.2 inches and a width of 5.05
Answers
Answer:
40.5 inches
Step-by-step explanation:
15.2*2+5.05*2=30.4+10.1=40.5
what is the equivalent to 178 and 739
Answers
The answer is 917
(Hope this helps you! :) )
PLEASE HELP !!! I’LL GIVE CROWN / COINS

Answers
Answer:
-81i
Step-by-step explanation:
(-3i)^3(-3)=-81i
Marian Plunket owns her own business and is considering an investment. if she undertakes the investment, it will pay $28,000 at the end of each of the new 3 years. the opportunity requires an initial investment of $7,000 plus an additional investment at the end of the second year of $35,000. what is the NPV of this opportunity if the interest rate is 8% per year? Should Marian take it?
Answers
The NPV is positive, it is worth taking the Investment.
Net Present Value (NPV) is an assessment method that determines the attractiveness of an investment. It is a technique that determines whether an investment has a positive or negative present value.
This method involves determining the future cash inflows and outflows and adjusting them to their present value. This helps determine the profitability of the investment, taking into account the time value of money and inflation.The formula for calculating NPV is:
NPV = Σ [CFt / (1 + r)t] – CIWhere CFt = the expected cash flow in period t, r = the discount rate, and CI = the initial investment.
The given problem can be solved by using the following steps:
Calculate the present value (PV) of the expected cash inflows:
Year 1: $28,000 / (1 + 0.08)¹ = $25,925.93Year 2: $28,000 / (1 + 0.08)² = $24,009.11Year 3: $28,000 / (1 + 0.08)³ = $22,173.78Total PV = $72,108.82
Calculate the PV of the initial investment: CI = $7,000 / (1 + 0.08)¹ + $35,000 / (1 + 0.08)²CI = $37,287.43Calculate the NPV by subtracting the initial investment from the total PV: NPV = $72,108.82 – $37,287.43 = $34,821.39
Since the NPV is positive, it is worth taking the investment.
For more questions on Investment.
https://brainly.com/question/29227456
#SPJ8
What is the inequality for this verbal description?
Kyle has d dollars to spend at the garden store. He wants to buy one small
tree for $9.00 and s pounds of soil that cost $5.00 per pound. Which
inequality represents this situation?
Answers
The inequality based on the given data is :
d ≥ 5s + 9 .
What is inequality?An inequality is a relationship that compares two numbers or other mathematical expressions that are not equal. It is most commonly used to compare the sizes of two numbers on a number line.Steps to solve inequality:Step 1: Eliminate fractions by multiplying all terms by the least common denominator of all fractions to solve an inequality.
Step 2 Simplify the inequality by combining like terms on each side.
Step 3 Subtract or add amounts to get the unknown on one side and the numbers on the other.
Here given,
Fixed cost = $9.00
Cost per pound of soil is $5.00
Hence, the equation will be :
d ≥ 5s + 9
Since d must be greater than or equal to this value for Kyle to be able to afford it.
∴ The inequality = d ≥ 5s + 9 .
To learn more about inequality refer to :
https://brainly.com/question/25275758
#SPJ1
What is the formula for calculating angle?
Answers
Angles Formulas at the center of a circle can be expressed as:
Central angle, θ = (Arc length × 360º)/(2πr) degrees
Sum of Interior angles=180°(n-2)
The angles formulas are used to find the measures of the angles. An angle is formed by two intersecting rays, called the arms of the angle, sharing a common endpoint.
The corner point of the angle is known as the vertex of the angle. The angle is defined as the measure of the turn between the two lines.
There are various types of formulas for finding an angle; some of them are the central angle formula, double-angle formula, etc...
We use the central angle formula to determine the angle of a segment made in a circle.
We use the sum of the interior angles formula to determine the missing angle in a polygon.
To know more about Angle Formula:
https://brainly.com/question/25716982
#SPJ4
9x − 9y = 18
y = 8
Solve a system of equations using substitution.
Answers
Answer: x = 10
Step-by-step explanation:
Answer: x=10
Step-by-step explanation: 9(8)= 72, 72+18=90, 90/9= 10
Solve for x ax-bx/x+c = d, if a =/b+d

Answers
Answer:
dc/a-b-d
Step-by-step explanation:
ax – bx = d
x + c
Multiply both sides by x + c
ax – bx
(x + c) = d(x + c)
x + c
Simplify
ax – bx
(x+c): ax – bx
x + c
ax – bx = d(x+c)
Expand d(x+c): dx + cd
ax — bx = dx + cd
Subtract dx from both sides
ax – bx – dx = dx + cd – dx
Simplify
ax – bx – dx = cd
Factor ax – bx – dx: x(a – b – d)
x(a - b- d) = cd
Divide both sides by a – b – d; a + b + d
x(a – b - d) cd
a + b + d
a - b - d
a – b-d
Simplify
X =dc/a-b-d
The value of 'x' in the algebraic equation is \(\rm x= \frac{dc}{a-b-d} \\\) where \(\rm a\neq b+d\)
It is given that the algebraic equation \(\rm \frac{ax-bx}{x+c}= d\)
It is required to solve the algebraic (polynomial) equation if \(\rm a\neq b+d\)
What is polynomial?Polynomial is the combination of variables and constants in a systematic manner with "n" number of power in ascending or descending order.
We have an algebraic equation:
\(\rm \frac{ax-bx}{x+c}= d\)
\(\rm \frac{ax-bx}{x+c}= d\\\\\rm ax-bx=d(x+c)\\\rm ax-bx=dx+dc\\\rm ax-bx-dx=dc\\\rm (a-b-d)x=dc\\\\\rm x= \frac{dc}{a-b-d} \\\)
Thus, the value of 'x' in the algebraic equation is \(\rm x= \frac{dc}{a-b-d} \\\) where \(\rm a\neq b+d\)
Learn more about Polynomial here:
brainly.com/question/17822016
Swiss is a built-in r data frame giving standardized fertility measure and socio-economic indicators for each of 47 french-speaking provinces of switzerland at about 1888.. we are interested in some descriptive statistics related to the agriculture column of swiss. we can access the data directly by using the assignment x <- swiss$agriculture. (in r use ?swiss for info on this dataset.) remember: x <- swiss$agriculture a. Calculate the sample median of x. b. Using the r quantile function, find the .34 quantile of x.(34th percentile) c. Calculate the interquartile range of x using r.
Answers
X is the variable that we have assigned the agriculture column of swiss to. Running this code would give us the interquartile range of x.
a. To calculate the sample median of x, we can use the median function in R. So, the code would be:
median(x)
where x is the variable that we have assigned the agriculture column of swiss to. Running this code would give us the sample median of x.
b. To find the .34 quantile of x, we can use the quantile function in R. The code would be:
quantile(x, 0.34)
where x is the variable that we have assigned the agriculture column of swiss to, and 0.34 represents the desired quantile. Running this code would give us the value of the .34 quantile of x.
c. To calculate the interquartile range of x, we can use the IQR function in R. The code would be:
IQR(x)
where x is the variable that we have assigned the agriculture column of swiss to. Running this code would give us the interquartile range of x.
The "fertility", "Switzerland", and "x <- swiss $ agriculture" terms.
a. To calculate the sample median of x (the agriculture column in the Swiss dataset), use the following R command:
median_x <- median(swiss$agriculture)
b. To find the 34th percentile (0.34 quantile) of x using the R quantile function, use the following R command:
quantile_x <- quantile(swiss$agriculture, probs = 0.34)
c. To calculate the interquartile range of x (the agriculture column in the Swiss dataset) using R, use the following R commands:
Q1 <- quantile(swiss$agriculture, probs = 0.25)
Q3 <- quantile(swiss$agriculture, probs = 0.75)
IQR_x <- Q3 - Q1
This will give you the interquartile range (IQR) of the agriculture column in the Swiss dataset.
Visit here to learn more about interquartile range:
brainly.com/question/29204101
#SPJ11
f(x)=2x+5 find f(-6)
Answers
Answer:
Step-by-step explanation:
f(x) = 2x + 5
f(-6)= 2(-6) + 5 = -12 + 5 = -7
Help with my maths plz

Answers
Answer:
25 and 36
Step-by-step explanation:
1x1=1
2x2=4
3x3=9
4x4=16
5x5=25
6x6=36
7x7=49
and so on..............
What is the equation of the line that passes through the point (−4, 8)
and has a slope of zero?
Answers
Answer:
y=8
Step-by-step explanation:
Slope-intercept form
y=mx+b
Plug in values
y=0x+b
8=0(-4)+b
b=8
substitute
y=8
D
C
6. ABCD is a rhombus.
BCE is an isosceles
triangle.
ABE is a straight line.
Work out the size of angle
DCA
a
480
Answers
The size of angle DCA is 480°.
How to find the size of angle DCA in the given figure?In the given figure, ABCD is a rhombus with angle ABE as a straight line and BCE as an isosceles triangle. We are asked to find the measure of angle DCA.
Since ABCD is a rhombus, opposite angles are congruent. Therefore, angle ACD is equal to angle ABC.
Since BCE is an isosceles triangle, angle BEC is equal to angle BCE.
From the given information, we know that angle ABC + angle BCE + angle ECD = 180 degrees.
Let's denote the measure of angle BCE as "x." Therefore, angle ABC is also "x."
Substituting these values into the equation, we have:
x + x + angle ECD = 180
2x + angle ECD = 180
Since angle ECD is denoted as 480 degrees in the question, we can solve for "x" as follows:
2x + 480 = 180
2x = 180 - 480
2x = -300
x = -150
However, angles cannot have negative measures. Therefore, there is no valid measure for angle DCA given the information provided.
Learn more about triangle
brainly.com/question/2773823
#SPJ11
Solve the inequality for x and identify the graph for its solution |x+3|>2
Answers
Answer:
Inequality Form:
x<−5 or x>−1
Interval Notation:
(−∞,−5)∪(−1,∞)
Step-by-step explanation:

A man runs the London marathon at an average speed of 8mph the route is 26 miles what was his time in hours and minutes
Answers
Answer:
the only thing you need to do is to divide the speed with the distance
What is the area of the figure
A 234 in
B 315 in
C 225 in
D 252 in

Answers
evaluate (-3) (-10) answer
dddddd
Answers
Answer:
30 because negative x negative = a positive number
The force, F (Newtons), between two objects is inversely proportional to the square of the distance,
d (metres), between them. The force is 0.005 Newtons when the distance between the objects is 2 metres.
Work out d (rounded to 2 DP) when F=0.048 Newtons.

Answers
Answer:
0.65 m to 2 D.P.s
Step-by-step explanation:
F = k/d^2
0.005 = k/2^2
k = 0.005 * 4
k = 0.02.
So F = 0.02/d^2.
When F = 0.048:
0.048 = 0.02/d^2
d^2 = 0.02/0.048
d^2 = 0.41666...
d = √0.41666...
= 0.645497.
Tina__________ 4 by_____________ to get 16 and 9 by____________ to get 81. She should have multiplied each term by__________ number.
Answers
Answer:
multiplied 4
9 the same
Step-by-step explanation:
Tina multiplied 4 by 4 to get 16, and 9 by 9 to get 81. she should have multiplied each term by the same number.
Solve the following equation for x.

Answers
Answer:
48
Step-by-step explanation:
jhus cross multiply 12*4=48
Answer:
x = 48
Step-by-step explanation:
x/4 = 12
4x/4 = x = 4(12) = 48
Check answer: 48/4 = 12
∫x216−x2−−−−−−√ dx= 8arcsin(x/4)-4sin(2arcsinx/4) functionsequation editor c (your final answer should be in terms of only x .) note: you can earn partial credit on this problem.
Answers
The final answer is 8arcsin(x/4) - 4sin(2arcsin(x/4)) + C, where C represents the constant of integration. The expression is given in terms of x only.
To evaluate the given integral, we can use trigonometric substitution. Let's substitute x = 4sinθ, which allows us to rewrite the integrand in terms of θ. The differential becomes dx = 4cosθ dθ.
Using this substitution, the integral transforms into ∫(4sinθ)²√(16-(4sinθ)²)(4cosθ) dθ. Simplifying this expression yields 16∫sin²θ√(1-cos²θ)cosθ dθ.
We can apply the double-angle identity sin²θ = (1-cos2θ)/2 to simplify further. This results in 8∫(1-cos2θ)√(1-cos²θ)cosθ dθ.
Next, we can apply the trigonometric identity sin(2θ) = 2sinθcosθ to obtain 8∫(sinθ-sin³θ) dθ.
Finally, integrating term by term and substituting back x = 4sinθ, we arrive at the final answer of 8arcsin(x/4) - 4sin(2arcsin(x/4)) + C. This expression represents the antiderivative of the given function in terms of x only, where C represents the constant of integration.
Learn more about trigonometric substitution here:
https://brainly.com/question/32150762
#SPJ11
write the equation of the circle in standard form: Center (7,0) R=1
Answers
Answer:
\((x-7)^2+y^2=1\)
Step-by-step explanation:
Hi there!
Equation of a circle: \((x-h)^2+(y-k)^2=r^2\) where the circle is centered at (h,k) and the radius is r
1) Plug in the given center (7,0)
\((x-7)^2+(y-0)^2=r^2\\(x-7)^2+y^2=r^2\)
2) Plug in the radius (1)
\((x-7)^2+y^2=1^2\\(x-7)^2+y^2=1\)
I hope this helps!
EXAMPLE: Empirical Rule
Suppose that 280 sociology students take an exam and that the distribution of their scores can be treated as normal. Find the number of scores falling within 2 standard deviations of the mean.
Answers
Approximately 188 values fall within 2 standard deviations of the mean when 280 sociology students take an exam and the distribution of their scores can be treated as normal.
It states that the grade distribution of 280 sociology students can be considered normal. Let μ be the average score of the students and σ be the standard deviation.
A run appear of thumb is that nearly 68% of the comes almost are interior 1 standard deviation of the pitiless, nearly 95% of the comes around are interior 2 standard deviations of the brutal, and nearly 99.7% of the comes approximately are interior 3 standard deviations of the cruel.
Since we are interested in finding the number of values within 2 standard deviations of the mean, we can estimate this using a rule of thumb.
We know that about 95% of the results are within 2 standard deviations of the mean. So you can write:
P(μ - 2σ < X < μ + 2σ) = 0.95
where X is the student's score.
We can simplify this expression by subtracting μ from both sides.
P(-2σ < X - μ < 2σ) = 0.95
Now we can find the probability that the standard normal variable Z falls between -2 and 2 using the standard normal distribution. we have:
P(-2 < Z < 2) = 0.95
Using a standard normal distribution table or a calculator capable of calculating the normal probability, we can find that the probability that Z is between -2 and 2 is approximately 0.9545.
So it looks like this:
P(-2 < Z < 2) = P((X - μ)/σ < 2) - P((X - μ)/σ < -2) = 0.9545
Using a standard normal distribution table or a calculator capable of calculating the inverse normal probability, we find that a value of 2 in the standard normal distribution corresponds to a z-score of approximately 1.96.
So it looks like this:
P((X - μ)/σ < 1.96) - P((X - μ)/σ < -1.96) = 0.9545
Since the distribution of values is normal, we know that the standard normal variable (X - μ)/σ follows the standard normal distribution. Therefore, you can find the z-score corresponding to 1.96 using a standard normal distribution table or a calculator capable of calculating the inverse normal probability.
A z-score equal to 1.96 is found to be approximately 0.975.
So it looks like this:
P(Z < 0.975) - P(Z < -0.975) = 0.9545
Using a standard normal distribution table or a calculator capable of calculating normal probabilities, we find:
P(Z < 0.975) = 0.8365 and P(Z < -0.975) = 0.1635
So it looks like this:
0.8365 - 0.1635 = 0.673
Subsequently, roughly 67.3% of the comes about are inside 2 standard deviations of the mean.
To discover the number of comes about that are inside two standard deviations of the cruel, we have to increase that rate by the entire number of understudies.
Number of outcomes within 2 standard deviations of the mean = 0.673 × 280 ≈ 188
Therefore, approximately 188 values fall within 2 standard deviations of the mean.
learn more about standard deviation
brainly.com/question/23907081
#SPJ4
The graph of the function f(x)=-(x+3)(x-1) is shown below. What is true about the domain and range of the function?

Answers
Answer:
The 3rd one is correct.
Step-by-step explanation:
what is the name of the length of the straight line drawn from an object’s initial position to the object’s final position?
Answers
Displacement is the length of the straight line drawn from an object’s initial position to the object’s final position
The term "displacement" refers to a change in an object's position. It is a vector quantity with a magnitude and direction. The symbol for it is an arrow pointing from the initial position to the ending position. For instance, if an object shifts from position A to position B, its position changes.
If an object moves with respect to a reference frame, such as when a passenger moves to the back of an airplane or a professor moves to the right with respect to a whiteboard, the object's position changes. This change in location is described as displacement.
The displacement is the shortest distance between an object's initial and final positions. Displacement is a vector. It is visualized as an arrow that points from the initial position to the final position, indicating that it has both a direction and a magnitude.
Learn more about displacement at:
https://brainly.com/question/14422259
#SPJ4
