Answers
Answer:
x=6
Step-by-step explanation:
25+133+4+3x=180
3x=180-162
3x=18
x=6
Related Questions
An equilateral triangle has a perimeter of 12 x + 18 units. Which expression can be used to show the length of one side of the triangle?
6 (2 x + 3): Each side length is 2 x + 3 units.
3 (4 x + 6): Each side length is 4 x + 6 units.
2 (6 x + 9): Each side length is 6 x + 9 units.
x (12 + 18): Each side length is 12 + 18 units.
Answers
Answer:
3 (4 x + 6): Each side length is 4 x + 6 units.
Step-by-step explanation:
Perimeter of equilateral triangle = 12x + 18 = 3(4x + 6) units
Answer:
B
Step-by-step explanation:
An equilateral triangle has a perimeter of 12 x + 18 units. Which expression can be used to show the length of one side of the triangle?
6 (2 x + 3): Each side length is 2 x + 3 units.
✔3 (4 x + 6): Each side length is 4 x + 6 units.
2 (6 x + 9): Each side length is 6 x + 9 units.
x (12 + 18): Each side length is 12 + 18 units.
The diameter of a turbine shaft in a manufacturing facility is normally distributed, with a mean of 100 millimeters and a standard deviation of 20 millimeters. a. What is the probability of a part having a diameter of at least 130 millimeters? b. What is the probability of a part having a diameter no greater than 130 millimeters? c. What is the probability of a part having a diameter between 100 and 130 millimeters? d. What is the probability of a part having a diameter between 70 and 100 millimeters?
Answers
The probability of a part having a diameter of at least 130 millimeters is 0.1587. The probability of a part having a diameter no greater than 130 millimeters is 0.8413. The probability of a part having a diameter between 100 and 130 millimeters is 0.3413. The probability of a part having a diameter between 70 and 100 millimeters is 0.2773.
(a) The probability of a part having a diameter of at least 130 millimeters is calculated by finding the area under the standard normal curve to the right of 130. This area is 0.1587.
(b) The probability of a part having a diameter no greater than 130 millimeters is calculated by finding the area under the standard normal curve to the left of 130. This area is 0.8413.
(c) The probability of a part having a diameter between 100 and 130 millimeters is calculated by finding the area under the standard normal curve between 100 and 130. This area is 0.3413.
(d) The probability of a part having a diameter between 70 and 100 millimeters is calculated by finding the area under the standard normal curve between 70 and 100. This area is 0.2773.
The standard normal curve is a bell-shaped curve that is used to represent the probability of a standard normal variable. The standard normal variable is a variable that has a mean of 0 and a standard deviation of 1.
The probability of a part having a diameter of at least 130 millimeters is 0.1587, which means that there is a 15.87% chance that a randomly selected part will have a diameter of at least 130 millimeters.
The probability of a part having a diameter no greater than 130 millimeters is 0.8413, which means that there is an 84.13% chance that a randomly selected part will have a diameter of no greater than 130 millimeters.
The probability of a part having a diameter between 100 and 130 millimeters is 0.3413, which means that there is a 34.13% chance that a randomly selected part will have a diameter between 100 and 130 millimeters.
The probability of a part having a diameter between 70 and 100 millimeters is 0.2773, which means that there is a 27.73% chance that a randomly selected part will have a diameter between 70 and 100 millimeters.
Visit here to learn more about probability:
brainly.com/question/13604758
#SPJ11
PLEASEE HELPP !! willing to help with history/ss if you answer
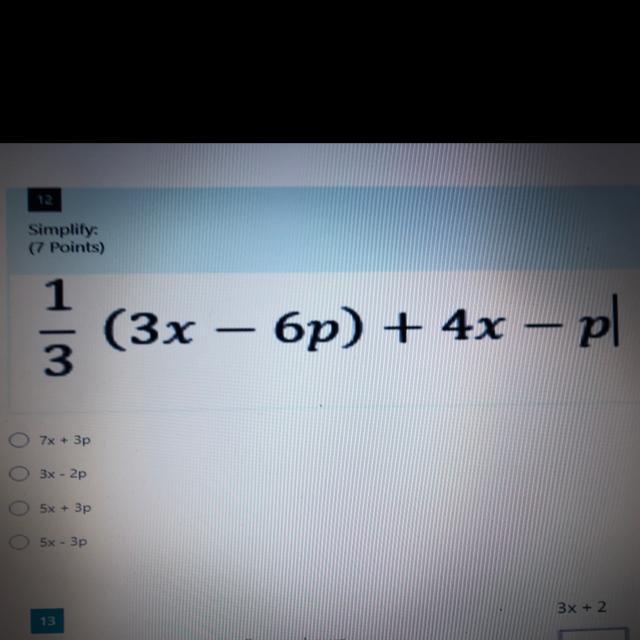
Answers
Answer:
Solution:-First write the given polynomial\(\qquad\quad {:}\longrightarrow\sf {\mid} \dfrac {1}{\cancel3}}(\bcancel {3}x-6p)+4x-p{\mid}\)
Simplify\(\qquad\quad {:}\longrightarrow\sf {\mid}(x-6p)+4x-p {\mid}\)
\(\qquad\quad {:}\longrightarrow\sf x-6p+4x-p \)
Combine like polynomials\(\qquad\quad {:}\longrightarrow\sf x-4x-6p-p \)
Add and subtract accordingly\(\qquad\quad {:}\longrightarrow\sf -3x-5p \)
which choice is equivalent to the expression below 2^7 times 19
Answers
The expression 2^7 times 19 can be simplified by first evaluating the exponential term, 2^7, which is equal to 128. Therefore:2^7 times 19 = 128 * 19We can then evaluate the product of 128 and 19 using multiplication. When we do that, we get:2^7 times 19 = 2432Therefore, the choice that is equivalent to the expression 2^7 times 19 is 2432
can someone help me before 11:59 pls

Answers
Answer: can you help me i cant put a q i have to points
Step-by-step explanation: plssssssssssssssss
A customer wanted to purchase a video game and realized that they were short $4.28 to be able to pay. Which value is the opposite of being short $4.28
Camila ubicó 90 botellas en una estantería de un supermercado y de ellas eran de jugo sin azúcar.Si los jugos sin azúcar tienen tres sabores diferentes y Camila puso la misma cantidad de cada sabor en la estantería, ¿con cuál de las siguientes operaciones se calcula la cantidad de botellas de jugo sin azúcar de cada sabor que puso Camila en la estantería?
Answers
Camila puso 30 botellas de cada sabor en la estantería.
Dado que Camila ubicó 90 botellas en una estantería de un supermercado, y los jugos sin azúcar tienen tres sabores diferentes y Camila puso la misma cantidad de cada sabor en la estantería, para determinar la cantidad de botellas de jugo sin azúcar de cada sabor que puso Camila en la estantería se debe realizar el siguiente cálculo:
90/3 = X30 = XPor lo tanto, Camila puso 30 botellas de cada sabor en la estantería.
Aprende más en https://brainly.com/question/16991787
Will give BRANLIEST PLEASE HELP
Answers
Answer: n=6
Step-by-step explanation:
To solve this proportion, you solve this as you would any proportion. You would have to first cross multiply.
\(\frac{1}{5}(15)=\frac{1}{2}n\)
\(3=\frac{1}2}n\) [multiply both sides by 2]
\(n=6\)
3] Question 5 Consider the vector field F(x, y, z) = y cos (xy) i + x cos (xy)j – sin zk. (i) Calculate the curl of the vector field F. State whether F is conservative. (ii) Let C be the curve joining the origin (0,1,-1) to the point with coordinates (1, 2V2,2) defined by the following parametric curve r(t) = n* i + t}j + tcos atk, 15t52. Calculate the scalar line integral of the vector field. F. dr. F.dr.
Answers
Given vector field, F(x, y, z) = y cos (xy) i + x cos (xy) j – sin z k To calculate the curl of F, we need to take the curl of each component and subtract as follows,∇ × F = ( ∂Q/∂y - ∂P/∂z ) i + ( ∂P/∂z - ∂R/∂x ) j + ( ∂R/∂x - ∂Q/∂y ) k...where P = y cos(xy), Q = x cos(xy), R = -sin(z)
Now we calculate the partial derivatives as follows,
∂P/∂z = 0, ∂Q/∂y = cos(xy) - xy sin(xy), ∂R/∂x = 0...
and,
∂P/∂y = cos(xy) - xy sin(xy), ∂Q/∂z = 0, ∂R/∂y = 0
Therefore,
∇ × F = (cos(xy) - xy sin(xy)) i - sin(z)j
The curl of F is given by:
(cos(xy) - xy sin(xy)) i - sin(z)j.
To state whether F is conservative, we need to determine if it is a conservative field or not. This means that the curl of F should be zero for it to be conservative. The curl of F is not equal to zero. Hence, the vector field F is not conservative. Let C be the curve joining the origin (0,1,-1) to the point with coordinates (1, 2V2,2) defined by the following parametric curve:
r(t) = n* i + t}j + tcos atk, 15t52.
The curve C is defined as follows,r(t) = ni + tj + tk cos(at), 0 ≤ t ≤ 1Given vector field, F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk Using the curve parameterization, we get the line integral as follows,∫CF.dr = ∫10 F(r(t)).r'(t)dt...where r'(t) is the derivative of r(t) with respect to t
= ∫10 [(t cos(at))(cos(n t)) i + (n cos(nt))(cos(nt)) j + (-sin(tk cos(at)))(a sin(at)) k] . [i + j + a tk sin(at)] dt
= ∫10 [(t cos(at))(cos(n t)) + (n cos(nt))(cos(nt)) + (-a t sin(at) cos(tk))(a sin(at))] dt
= ∫10 [(t cos(at))(cos(n t)) + (n cos(nt))(cos(nt)) - a^2 (t/2) (sin(2at))] dt
= [sin(at) sin(nt) - (a/2) t^2 cos(2at)]0^1
= sin(a) sin(n) - (a/2) cos(2a)
The vector field F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk is given. Firstly, we need to calculate the curl of F. This involves taking the curl of each component of F and subtracting. After calculating the partial derivatives of each component, we get the curl of F as (cos(xy) - xy sin(xy)) i - sin(z)j. Next, we need to determine whether F is conservative. A conservative field has a curl equal to zero. As the curl of F is not equal to zero, it is not a conservative field. In the second part of the problem, we have to calculate the scalar line integral of the vector field F. dr along the curve C joining the origin to the point with coordinates (1, 2V2, 2). We use the curve parameterization to calculate the line integral. After simplifying the expression, we get the answer as sin(a) sin(n) - (a/2) cos(2a).
The curl of the given vector field F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk is (cos(xy) - xy sin(xy)) i - sin(z)j. F is not conservative as its curl is not zero. The scalar line integral of the vector field F along the curve C joining the origin to the point with coordinates (1, 2V2,2) is sin(a) sin(n) - (a/2) cos(2a).
To learn more about curve parameterization visit:
brainly.com/question/12982907
#SPJ11
3 2/5+3 2/5/2 1/12 what is theeeeee answerrrr
Answers
Answer:
the awnswer is 5.032\
Step-by-step explanation:
Because
3 2/5= 17/5
17/5+17/5 * 1/2* 1/12
Which
17/5 + 17/120= 85/24= 3 13/24
Hope this helps
A 6-foot man casts an 8-goot shadow. How tall is a tree that casts a 20-foot shadow?
Answers
Answer: 26.6 repeating number or 26 2/3
Step-by-step explanation:
Eli runs 5 meters per second.
On a coordinate plane, a line goes through points (1, 5) and (2, 10)..
Use the graph to identify the independent and the dependent variable. Check all that apply.
The two variables are Eli and 5.
The two variables are meters and seconds.
Meters are graphed on the x-axis.
Meters are graphed on the y-axis.
Seconds is the independent variable.
Seconds is the dependent variable.
Answers
Answer:
the two variables are meters and seconds,. meters are graphed on the y- axis, seconds is the independent variable....2,4,5
Answer:
right answer lol
Step-by-step explanation:

Will give crown help

Answers
Answer:
(2,-8)
Step-by-step explanation:
(2,-8)
Reggie plans to have a garden with 36 plants. He wants the ratio of tomato plants to cucumber plants to be 4:5. How many cucumber plants will be in Reggie's garden?
Answers
Answer:
20
Step-by-step explanation:
Total no of plants in a garden = 36
The ratio of tomato plants to cucumber plants to be 4:5.
Let tomato plants are 4x and cucumber plants is 5x.
ATQ,
4x+5x=36
9x = 36
x = 4
For cucumber plant, 5x = 5(4) = 20
So, there are 20 cucumber plants will be in Reggie's garden
by selling a chair for RS720 a garden gains be consumed by 40 horses
Answers
Answer:
this makes no sense
Step-by-step explanation:
thnx for the points
How did Mandela get the name “Nelson?”
Answers
Answer:
On the first day of school his teacher, Miss Mdingane, gave each of the students an English name. This was the custom among Africans in those days and was undoubtedly due to the British bias of education. That day, Miss Mdingane told him that his new name was Nelson.
The midpoint of GH is M(-5, 4). One endpoint is H (-8, 0).
Find the coordinates of end point G
Answers
Answer:
G (-2,8)
Step-by-step explanation:
(-8+x)/2 = -5
-8 + x = -10
x = -10 + 8
x = -2
(0+y)/2 = 4
y = 4 · 2
y = 8
find the quotient jenny made a 9-inch sub sandwich she need to cut into 2/3 piece. how many pieces will she be able to cut?
Answers
27/2 or 13.5 pieces.
To find the quotient, we need to divide the length of the sub sandwich by the length of each piece she wants to cut it into:
9 ÷ (2/3)
We can simplify this by multiplying the numerator by the reciprocal of the denominator:
9 ÷ (2/3) = 9 × (3/2)
Multiplying straight across:
9 × (3/2) = 27/2
So Jenny will be able to cut the sub sandwich into 27/2 or 13.5 pieces.
Step-by-step explanation:
Cutting a 9 inch sub into 2/3 inch pieces ?
9 inch / 2/3 inch / piece = 9 * 3/2= 27/2 = 13.5 pieces ~ 13 with a bit left over
BRAINLIEST! URGENT! Please help, I've been stuck on this problem for a while now. If you know the answer, please provide an explanation. Thank you.

Answers
C is the answer
The axioms for a vector space V can be used to prove the elementary properties for Suppose that win V has the property that u + w=w+u= u for all u in V. In a vector space. Because of Axiom 2. Axioms 2 and 4 imply, respectlyely, that particular, 0 + w=0. But 0 + w=w by Axiom Hence, w=w+0 = 0 +w=0. 0-u u and -u+u = 0 for all u.
Answers
The given statements discuss properties of a vector space V, particularly focusing on the property of a vector w that satisfies u + w = w + u = u for all u in V.
Based on the provided information, it can be inferred that this property implies certain elementary properties of vector addition and scalar multiplication in V. Specifically, it suggests that adding the zero vector to any vector w results in w, and that subtracting a vector u from itself yields the zero vector.
Additionally, it suggests that the sum of a vector u and its additive inverse, denoted as -u, equals the zero vector. These conclusions can be derived using the axioms of vector spaces, which provide the foundational rules for vector operations.
To learn more about vector operations click here
brainly.com/question/10164701
#SPJ11
if a population begins with 25 individuals and grows exponentially for 20 generations with an r value of 0.2, then the greatest percentage increase will occur: please choose the correct answer from the following choices, and then select the submit answer button. answer choices from generation 11 to 12. from generation 5 to 6. from generation 1 to 2. from generation 19 to 20.
Answers
Answer: from generation 19 to 20.
Step-by-step explanation:
The greatest percentage increase will occur from generation 19 to 20 as the exponential power will be highest.
What is exponential growth?
Exponential growth happens once the larger in size you're the quicker you grow that causes you to even larger in size. it's the expansion characterised by interest, or growth. it's known as exponential growth as a result of it will solely be delineate mathematically by inserting time within the exponent or power of the bottom. Population then is adequate to the population at the current times some discretional range to the facility of the expansion rate times the time. The discretional range is sometimes two then the expansion rates is given because the reciprocal of the doubling time.
Main body:
initial population = 25
Total generation = 20
growth rate = 0.2
General formula of exponential function = aˣ
here a = 25 and x = 0.2
⇒25⁰°²
= 1.9
hence total population = 25+2 = 27
So it is clear that in 19 to 20 generation , growth will be highest.
To know more about exponential growth , visit:
https://brainly.com/question/11975096
#SPJ4
12,000,055 + 60 + 16 + 90 x 40
Answers
Answer:
12003731
(12,000,055 + 60 + 16 + 90 x 40=12003731)
find the probability

Answers
Answer:
alright so you have to do math to do it
Step-by-step explanation:
I need help ASAP pls

Answers
Answer:
it not clear maybe you can take an other pohto
sorry
Step-by-step explanation:
if it is known that at least one child has blue eyes, what is the probability that at least two children have blue eyes?
Answers
Answer: 1 in 2 chance
Step-by-step explanation:
will mark brainliest!!

Answers
Answer:
d
Step-by-step explanation:
Answer:
Step-by-step explanation:
b) m+g < and = 20
re arrange
m < and = 20- g
put values of g to find value of m that will always be less or equal
similarly,
15m +20g > and = 300
re arrange m >= \(\frac{300-20g}{15}\)
put different values of g to find different values of m which will always be greater or equal.
c) intersecting points of the graph
pleeease help will give brainliest

Answers
Answer:
2x,5x
Step-by-step explanation:
thats right I am not smart
Answer:
(x,y) = ( -6,8)
Step-by-step explanation:
waiting for brainlist
name the property the equation illustrates-4 x -1/4 = 1
Answers
The equation -4 x -1/4 = 1 illustrates the commutative property of multiplication.
The commutative property of multiplication states that changing the order of the factors does not change the product. In other words, for any two numbers a and b, the product of a x b is equal to the product of b x a.
In the given equation, we have -4 x -1/4 = 1. By applying the commutative property of multiplication, we can rearrange the factors:
-4 x -1/4 = -1/4 x -4
Since the commutative property of multiplication holds true, we can rewrite the equation as:
-1/4 x -4 = 1
The result of multiplying -1/4 by -4 is indeed 1. This confirms that the equation satisfies the commutative property of multiplication.
In conclusion, the equation -4 x -1/4 = 1 demonstrates the commutative property of multiplication, which states that the order of the factors can be changed without affecting the product.
Learn more about multiplication here:
https://brainly.com/question/11527721
#SPJ11
Which system of inequalities is represented on this graph?
SOME ONE PLEASE HELP!!

Answers
Answer:
B
Step-by-step explanation:
It is the answer good luck in your test
Find the area of the region bounded by the parabola y = 4x^2, the tangent line to this parabola at (2, 16), and the x-axis.
you must use integration to solve the problem and the answer cannot include variables of x and y. Please solve completely.
Answers
To find the area of the region bounded by the parabola y = 4x², the tangent line to this parabola at (2, 16), and the x-axis, we will integrate the area between the curve and the x-axis on the interval (0,2) and then subtract the area of the triangle formed by the tangent line, x-axis, and the vertical line x=2.
Here's the complete solution:Step 1: Find the equation of the tangent line at (2,16)The derivative of y = 4x² is:y' = 8xThus, the slope of the tangent line at (2,16) is:y'(2) = 8(2) = 16The point-slope form of the equation of a line is:y - y₁ = m(x - x₁)Using point (2,16) and slope 16, the equation of the tangent line is:y - 16 = 16(x - 2)y - 16 = 16x - 32y = 16x - 16Step 2: Find the x-coordinate of the intersection between the parabola and the tangent line.To find the x-coordinate, we equate the equations:y = 4x²y = 16x - 16Substituting the first equation into the second gives:4x² = 16x - 16Simplifying, we get:4x² - 16x + 16 = 04(x - 2)² = 0x = 2Since the x-coordinate of the point of intersection is 2, this is the right endpoint of our integration interval.Step 3: Integrate the region bounded by the parabola and the x-axis on the interval (0,2)We need to integrate the curve y = 4x² on the interval (0,2):∫(0 to 2) 4x² dx= [4x³/3] from 0 to 2= (4(2)³/3) - (4(0)³/3)= (32/3)Thus, the area between the curve and the x-axis on the interval (0,2) is 32/3.Step 4: Find the area of the triangle formed by the tangent line, x-axis, and the vertical line x=2To find the area of the triangle, we need to find the height and base.The base is the vertical line x=2, so its length is 2.The height is the distance between the x-axis and the tangent line at x=2, which is 16. Thus, the area of the triangle is:1/2 * base * height= 1/2 * 2 * 16= 16Step 5: Subtract the area of the triangle from the area of the region bounded by the parabola and the x-axis on the interval (0,2)Area of the region = (32/3) - 16= (32 - 48)/3= -16/3Therefore, the area of the region bounded by the parabola y = 4x², the tangent line to this parabola at (2, 16), and the x-axis is -16/3.
to know more about region visit:
https://brainly.in/question/48378001
#SPJ11
The parabola is defined by the equation \(y = 4x².\)
We need to find the area of the region bounded by this parabola, the tangent line to this parabola at (2, 16), and the x-axis.
This is illustrated in the figure below: Let's first find the equation of the tangent line at (2, 16).
The derivative of y = 4x² is:y' = 8x
\(y = 4x² is:y' = 8x\)
The slope of the tangent line at \((2, 16) is therefore: y'(2) = 8(2) = 16\)
The equation of the tangent line is therefore:y - 16 = 16(x - 2) => y = 16x - 16
\(y - 16 = 16(x - 2) => y = 16x - 16\)We can now find the intersection points of the parabola and the tangent line by solving the system of equations:\(4x² = 16x - 16 => 4x² - 16x + 16 = 0 => (2x - 4)² = 0\)
Therefore, x = 2 is the only intersection point.
This means that the region is bounded by the x-axis on the left, the parabola above, and the tangent line below.
To find the area of this region, we need to integrate the difference between the parabola and the tangent line from x = 0 to x = 2.
This gives us the area of the shaded region in the figure above.
Using the equations of the parabola and the tangent line, we have:\(y = 4x²y = 16x - 16\)
The difference between these two functions is:\(y - (16x - 16) = 4x² - 16x + 16\)
To find the area of the region, we need to integrate this function from x = 0 to x = 2.
That is, we need to compute the following definite integral: \(A = ∫[0,2] (4x² - 16x + 16) dxIntegrating term by term, we get: A = [4/3 x³ - 8x² + 16x]₀² = [4/3 (2)³ - 8(2)² + 16(2)] - [4/3 (0)³ - 8(0)² + 16(0)] = [32/3 - 32 + 32] - [0 - 0 + 0] = 32/3\)
Therefore, the area of the region bounded by the parabola \(y = 4x², the tangent line to this parabola at (2, 16), and the x-axis is 32/3 square units.\)
To know more about the word intersection visits :
https://brainly.com/question/24587393
#SPJ11
In a poll of 200 randomly selected U.S. adults, 104 said they favored a new proposition. Based on this poll, compute a 90% confidence interval for the proportion of all U.S. adults in favor of the proposition (at the time of the poll). Then complete the table below. Carry your intermediate computations to at least three decimal places. Round your answers to two decimal places. lower limit of 90%? upper limit of 90%
Answers
The lower limit of the 90% confidence interval is 0.429 when in a survey of 200 randomly chosen American adults, 104 responded in favor of the proposed proposal.
Given that
In a survey of 200 randomly chosen American adults, 104 responded in favor of the proposed proposal. Calculate a 90% confidence interval for the percentage of all U.S. adults who support the proposal based on the results of this poll (at the time of the poll). Complete the table below after that. Carry your calculations to a minimum of three decimal places.
We have to find the lower limit of 90%.
We know that
In a poll of 200 randomly selected U.S. Among adults, 104 expressed support for the novel idea.
p-hat = 104/200 = 0.52
ME = z×√[pq/n] = 2.5758×√[0.52*0.48/200] = 0.091
Now, the lower limit of the 90% confidence interval well be
p-hat-ME = 0.52-0.091 = 0.429
Therefore, The lower limit of the 90% confidence interval is 0.429 when in a survey of 200 randomly chosen American adults, 104 responded in favor of the proposed proposal.
To learn more about limit visit: https://brainly.com/question/29394831
#SPJ4
