Answers
R=3
V = pi * 9 * 20
V= 180 pi ( answer is A)
(Mark me the brainliest)
Related Questions
How far apart are the points (0,-1) and (6,5)?
Answers
Answer:
(6, 6)
Step-by-step explanation:
Answer:
The distance is 8.4853
Step-by-step explanation:
Input Data :
Point 1 (xA, yA) = (0, -1)
Point 2 (xB, yB) = (6, 5)
Objective :
Find the distance between two given points on a line?
Formula :
Distance between two points = √(xB − xA) ^ 2 + (yB − yA) ^ 2
Solution :
Distance between two points = √ (6 − 0)^2 + (5− −1) ^ 2
= √6^2 + 6^2
= √36 + 36
= √72
= 8.4853
Distance between points (0, -1) and (6, 5) is 8.4853
hope this helps and is right :)
As a general rule in computing the standard error of the sample mean, the finite population correction factor is used only if the:
Group of answer choices
1. sample size is more than half of the population size.
2. sample size is smaller than 5% of the population size.
3. sample size is greater than 5% of the sample size.
4. None of these choices.
Answers
The finite population correction factor is used in computing the standard error of the sample mean when the sample size is smaller than 5% of the population size.
The finite population correction factor is a adjustment made to the standard error of the sample mean when the sample is taken from a finite population, rather than an infinite population.
It accounts for the fact that sampling without replacement affects the variability of the sample mean.
When the sample size is relatively large compared to the population size (more than half), the effect of sampling without replacement becomes negligible, and the finite population correction factor is not necessary.
In this case, the standard error of the sample mean can be estimated using the formula for sampling with replacement.
On the other hand, when the sample size is small relative to the population size (less than 5%), the effect of sampling without replacement becomes more pronounced, and the finite population correction factor should be applied.
This correction adjusts the standard error to account for the finite population size and provides a more accurate estimate of the variability of the sample mean.
Therefore, the correct answer is option 2: the finite population correction factor is used when the sample size is smaller than 5% of the population size.
Learn more about mean here:
https://brainly.com/question/31101410
#SPJ11
Least common multiple of 15,24 by using prime factorization
Answers
Answer and Step-by-step explanation:
The least common multiple (LCM) of 15 and 24 can be found using the prime factorization of 15 and 24 which is...
The prime factorization of 15 is... 3 x 5.
The prime factorization of 24 is... 2 x 2 x 2 x 3.
Eliminate the duplicate factors of the two, then multiply them once with the remaining factors of the lists to get LCM (15,15) = 120.
Hope this helped you out! Have a wonderful day! <3
HELP MEH PLS! Will mark brainliest :3
Simplify it- don't solve it. Show your work too pls!

Answers
Answer:
Step-by-step explanation:
\((1/5k)^2=1/5^2*k^2\)
\(1/25*k^2=\frac{k^2}{25}\)
Answer: \(\frac{1}{25}k^2\)
This is equivalent to \(\frac{k^2}{25}\)
In decimal form, this is equivalent to 0.04k^2
==================================
Work Shown:
We have the two pieces 1/5 and k, all in the parenthesis being squared.
Square each piece
Squaring the piece 1/5 leads to (1/5)^2 = 1/25, since 5^2 = 25squaring the k value leads to k^2So overall, we end up with the answer \(\frac{1}{25}k^2\) which is equivalent to saying \(\frac{k^2}{25}\)
In decimal form, this is 0.04k^2 because 1/25 = 0.04
Anyone able to answer this?

Answers
Answer:
B) (4,5)
Step-by-step explanation:
Hope this helps.. (again)
Answer:
(4,5)
Step-by-step explanation:
you can count the units, move seven to the right and two up
Maggie drew triangle and then triangle . Triangle is congruent to triangle only if ∠ is equal to what value?
Include explanation!!

Answers
Answer:
Angle ABE = 58
Step-by-step explanation:
This would fulfill the AAA theorem, or 3 angles needing to be congruent. We got 58 by subtracting 89 and 62 from 180, then multiplying that answer by 2 (because it occupies both triangles).
MATH PROBLEM SOLVING

Answers
Answer:
Probability[Selected ball is a white ball without replacement (W)] = 5 / 22
Step-by-step explanation:
Given:
Number of white ball in jar = 5
Number of black ball in jar = 6
Find;
Probability[Selected ball is a white ball without replacement (W)]
Computation:
Probability of an event = Number of favorable outcomes / Total number of outcomes
Probability of 1st white ball = 5 / [5 + 6]
Probability of 1st white ball = 5 / 11
Probability of 2nd white ball [without replacement] = 5 / [11 - 1]
Probability of 2nd white ball [without replacement] = 5 / 10
Probability[Selected ball is a white ball without replacement (W)] = [5/11][5/10]
Probability[Selected ball is a white ball without replacement (W)] = 25 / 110
Probability[Selected ball is a white ball without replacement (W)] = 5 / 22
Find the value of x.

Answers
Answer:
x = 25
Step-by-step explanation:
One can use the Line Tangent to a Circle theorem to solve this problem. The Line Tangent to a Circle theorem states that when two non-parallel lines are tangent to a circle (the lines touch the circle at a single point), then the distance between the intersection point and the point of tangency is the same for both lines. This theorem does go by other names, but the actual theorem content is the same.
Using this one can form the equation;
BA = CA
Substitute,
2x + 3 = 53
Inverse operations,
2x + 3 = 53
-3 -3
2x = 50
/2 /2
x = 25
Identify the errors made in finding the inverse ofy = x2 + 12x.x= y2 + 12xy2 = x - 12xy2=-11xy=-11x, for x > 0Describe the three errors?
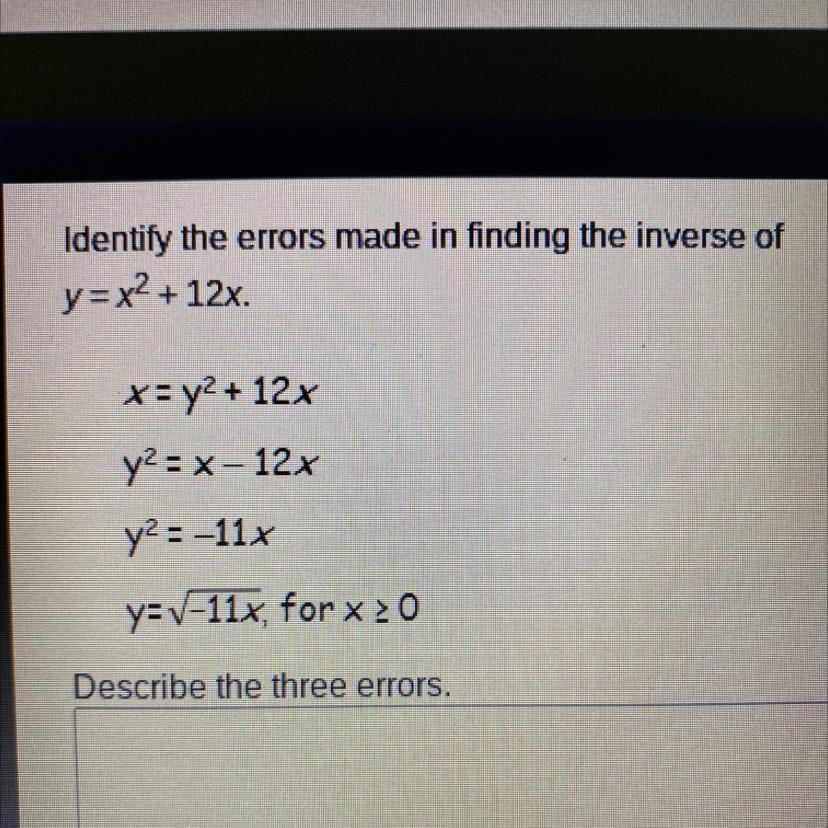
Answers
First, starting from the equation:
\(y=x^2+12x\)We should change every x for a y and every y for an x, so:
\(x=y^2+12y\)In the text, the first step was:
\(x=\questeq y^2+12x\)So, the first mistake was not to change the linear term 12x for 12y.
Another mistake was made from the following steps:
\(\begin{gathered} y^2=-11x \\ y=\sqrt[]{-11x},x\ge0 \end{gathered}\)The expression inside the square root must be greater or equal to 0, then:
\(\begin{gathered} -11x\ge0 \\ \Rightarrow x\le0 \end{gathered}\)So, the second mistake was not to identify the domain of x correctly.
A third mistake is that the square root of y^2 is not y, it is |y|. So:
\(\begin{gathered} y^2=-11x \\ \Rightarrow|y|=\sqrt[]{-11x} \\ \Rightarrow y=\pm\sqrt[]{-11x} \end{gathered}\)Determine the number of significant figures in each measurement. Then, choose the representation of the number where x is in place of the estimated digit from the measurement.a) 14.8mb) $10.25c) 0.05 Ld) 1.000 g/mLe) 6200cmf) 403 kg
Answers
Significant figures with representation of x are a) 14.8 m = 14.x m. b) $10.25 = 10.2x. c) 0.05 L = 0.0x L. d) 1.000 g/mL = 1.00x g/mL. e) 6200cm = 6200x cm. f) 403 kg = 40x kg.
a) 14.8m has 3 significant figures. Representation with x in place of estimated digit: 14.x m. b) $10.25 has 4 significant figures. Representation with x in place of estimated digit: 10.2x. c) 0.05 L has 1 significant figure. Representation with x in place of estimated digit: 0.0x L. d) 1.000 g/mL has 4 significant figures. Representation with x in place of estimated digit: 1.00x g/mL. e) 6200cm has 2 significant figures. Representation with x in place of estimated digit: 6200x cm. f) 403 kg has 3 significant figures. Representation with x in place of estimated digit: 40x kg. Significant figures are the digits in a measurement that are reliable and accurate. They provide an indication of the precision of a measurement, and allow us to communicate the level of certainty we have in a particular value. When determining the number of significant figures in a measurement, we typically follow a set of rules. Non-zero digits are always significant, zeros between non-zero digits are significant, and trailing zeros to the right of the decimal point are significant. Zeros at the beginning of a number or to the left of a non-zero digit are not significant. The use of significant figures is important in science and engineering to ensure accurate and reliable measurements. When performing calculations with measurements, the result should be reported with the same number of significant figures as the least precise measurement used in the calculation. In addition, when rounding a number, the last digit should be rounded to the nearest value consistent with the number of significant figures being used. Understanding significant figures is an important part of scientific and mathematical communication, and can help to ensure accuracy and consistency in the reporting of data and calculations.
To learn more about mathematical communication click here
brainly.com/question/29153641
#SPJ4
(1 point) find the interval of convergence for the power series ∑n=2[infinity](x−5)n3n
Answers
The interval of convergence for the given power series is (2, 8).
To find the interval of convergence for the given power series. We have the power series:
∑(n=2 to ∞) ((x-5)ⁿ)/(3ⁿ)
To find the interval of convergence, we'll use the Ratio Test. For the Ratio Test, we need to compute the limit:
L = lim (n → ∞) |(a_(n+1)/a_n)|
For our series, a_n = ((x-5)ⁿ)/(3ⁿ). Therefore, a_(n+1) = ((x-5)(n+1))/(3(n+1)). Now, let's compute the ratio:
|(a_(n+1)/a_n)| = |(((x-5)(n+1))/(3(n+1))) / (((x-5)ⁿ)/(3ⁿ))|
Simplify the expression:
|(a_(n+1)/a_n)| = |(x-5)/3|
The series converges if L < 1. So we have:
|(x-5)/3| < 1
Now, we'll solve for x to find the interval of convergence:
-1 < (x-5)/3 < 1
Multiply each term by 3:
-3 < x-5 < 3
Add 5 to each term:
2 < x < 8
You can learn more about convergence at: brainly.com/question/14394994
#SPJ11
Find a formula for the exponential function passing through thepoints (-1, 2/5 ) and (3,250)
Answers
The exponential function between (-1, 2/5) and (3, 250) is as follows:
\(f(x) = 2 * 5^x\)
By combining the fourth roots from both sides, we arrive at:
b = 5
When we use the expression we discovered for a and this value of b, we get:
a = (2/5) * 5 = 2
As a result, the exponential function between (-1, 2/5) and (3, 250) is as follows:
\(f(x) = 2 * 5^x\)
what are functions?A relation between a collection of inputs and outputs is known as a function. A function is, to put it simply, a relationship between inputs in which each input is connected to precisely one output. Each function has a range, codomain, and domain. The usual way to refer to a function is as f(x), where x is the input. A function is typically represented as y = f. (x).
In mathematics, a function is a unique arrangement of the inputs (also referred to as the domain) and their outputs (sometimes referred to as the codomain), where each input has exactly one output and the output can be linked to its input.
from the question:
This is the shape of the exponential function:
f(x) = a *\(b^x\)
where a represents the starting point and b represents the exponential function's base.
We must solve the system of equations to determine the values of a and b that meet the requirements:
a * \(b^(-1)\) = 2/5 (equation 1)
a *\(b^3\)= 250 (equation 2)
We can solve for an in equation 1 by multiplying both sides by b:
a = (2/5) * b
Substituting this expression into equation 2, we get:
(2/5) * b *\(b^3\) = 250
Simplifying, we get:
\(b^4 = 3125\)
By combining the fourth roots from both sides, we arrive at:
b = 5
When we use the expression we discovered for a and this value of b, we get:
a = (2/5) * 5 = 2
As a result, the exponential function between (-1, 2/5) and (3, 250) is as follows:
\(f(x) = 2 * 5^x\)
to know more about functions visit:
https://brainly.com/question/12431044
#SPJ1
If two amounts are ____________, you can substitute one for the other.
Answers
Answer:
equivalent
Step-by-step explanation:
Suppose x,y,z are any real numbers. Show that if x > y + z then there are rational numbers a > y and b > z such that
x > a + b.
Answers
To show that if x > y + z for any real numbers x, y, and z, there exist rational numbers a > y and b > z such that x > a + b, we can follow these steps:
1. Since x, y, and z are real numbers, we can find rational numbers between any two real numbers.
2. Let's find a rational number a such that y < a < x - z. Since y and x - z are real numbers, there must exist a rational number a between them.
3. Similarly, find a rational number b such that z < b < x - a. Since z and x - a are real numbers, there must exist a rational number b between them.
4. Now, we have y < a and z < b, which means a > y and b > z, satisfying the given conditions.
5. Since a > y and b > z, adding the two inequalities gives a + b > y + z.
6. We know that x > y + z, so combining this with the previous inequality gives x > a + b.
Thus, we have shown that if x > y + z for any real numbers x, y, and z, there exist rational numbers a > y and b > z such that x > a + b.
Learn more about real numbers at: https://brainly.com/question/17201233
#SPJ11
What is the mode?
9 4 6 3 9 3 10 4 6 4
Answers
Answer:
4
Explanation:
The mode is what number occurs most often
The mode for this question is 4
Mode
In a set of numbers, the mode is the number that occurs most often. In other words, it measures how frequently a particular number occurs within a set of numbers. It is a type of average, like its counterparts, the median and mean.
To find the mode of a set of numbers,
List the set of numbers in ascending or descending order, including any duplicatesCount the number of times each number in the set of numbers occurs. The number that occurs the highest number of times is the mode of the set of dataSolve the equation.
C3 = 216
Answers
Step-by-step explanation:
C= 72..............
C3=216
C=216
3
C = 72
Thanks
Answer:
\(c = 216 : c = 6, c = −3 + 3 3 i, c = −3 − 3 3 i3\\Simplify 6 ·2−1 − 3 i: − 3 − 3 3 i\)
Step-by-step explanation:
whats 1 + 1 plz answer
Answers
Answer:
2
Step-by-step explanation:
Thanks for the points Kiddo
Explain: add one plus the other one and that equals two
What is the green dashed line called?

Answers
Answer:
axis of symetry
Step-by-step explanation:
Beast_Building on yt
What is the rejection region in a one-tailed hypothesis test with a significance level of 0.05?
A) the upper 5% of the distribution
B) the lower 5% of the distribution
C) the upper 2.5% of the distribution
D) the lower 2.5% of the distribution
Answers
The rejection region in a one-tailed hypothesis test with a significance level of 0.05 is the upper 5% of the distribution. The correct answer is option A.
In a one-tailed hypothesis test with a significance level of 0.05, the rejection region is determined based on the tail of the distribution that corresponds to the alternative hypothesis. Since the significance level is 0.05, which means a 5% chance of making a Type I error, the rejection region will be either in the upper or lower tail of the distribution, depending on the direction of the alternative hypothesis.If the alternative hypothesis suggests that the parameter is greater than the null hypothesis value, the rejection region will be in the upper tail of the distribution. In this case, the correct choice would be: A) the upper 5% of the distributionIf the alternative hypothesis suggests that the parameter is smaller than the null hypothesis value, the rejection region will be in the lower tail of the distribution. In this case, the correct choice would be: B) the lower 5% of the distributionThere are two forms of the one-tailed test: a right-tailed test (a test where the rejection region is on the right-hand side of the sampling distribution) and a left-tailed test (a test where the rejection region is on the left-hand side of the sampling distribution).Thus, the rejection region in a one-tailed hypothesis test with a significance level of 0.05 is the upper 5% of the distribution.
For more questions on one-tailed hypothesis:
https://brainly.com/question/31367829
#SPJ8
Let f(x) = tan x, Show that f(0) = f(π) but there is no number c in (0, π) such that f’(c) = 0. Why does this not contradict Rolle’s Theorem?
Answers
This situation does not contradict Rolle's Theorem because Rolle's Theorem requires the function to be continuous on a closed interval and differentiable on an open interval, which is not satisfied by f(x) = tan x in the interval (0, π).
To show that f(0) = f(π), we evaluate the tangent function at these points. At x = 0, tan(0) = 0, and at x = π, tan(π) = 0. Therefore, f(0) = f(π).
To investigate whether there exists a number c in the interval (0, π) such that f'(c) = 0, we need to find the derivative of f(x). The derivative of tan x is given by f'(x) = sec² x. However, the secant squared function is never equal to zero. Therefore, there is no c in the interval (0, π) where f'(c) = 0.
This situation does not contradict Rolle's Theorem because Rolle's Theorem requires certain conditions to be met. First, the function must be continuous on the closed interval [a, b], which is not satisfied by f(x) = tan x since it is not defined at x = π/2. Second, the function must be differentiable on the open interval (a, b), but f'(x) = sec^2 x is not defined at x = π/2. Thus, the requirements of Rolle's Theorem are not fulfilled, and its conclusion does not apply to f(x) = tan x in the interval (0, π).
Learn more about Interval:
brainly.com/question/11051767
#SPJ11
find the finite difference uxx sin u = sin 3x
Answers
The exact solution will depend on the boundary conditions and the step size h chosen. In summary, the finite difference method is used to approximate the second derivative in the given trigonometric equation.
The Chain Rule formula is a formula for computing the derivative of the composition of two or more functions. Chain rule in differentiation is defined for composite functions. For instance, if f and g are functions, then the chain rule expresses the derivative of their composition.
d/dx [f(g(x))] = f'(g(x)) g'(x)
To find the finite difference uxx of the given equation sin u = sin 3x, we first need to apply the chain rule of differentiation twice. This gives us:
du/dx = u' = 3cos(3x)cos(u)
d^2u/dx^2 = u'' = -9sin(3x)cos(u)^2 - 3cos(3x)sin(u)u'
Next, we can substitute sin u = sin 3x into the equation:
sin 3x = -9sin(3x)cos(u)^2 - 3cos(3x)sin(u)u'
Now, we can use the formula for sin 3x in terms of sin x and cos x:
3sin(x) - 4sin^3(x) = -9[3sin(x) - 4sin^3(x)]cos(u)^2 - 3[4cos^2(x) - 1]sin(u)u'
Simplifying this equation and solving for u'', we get:
u'' = -6sin(x)cos(u)^2 + 2[3sin(x) - 4sin^3(x)]sin(u)u' / [9cos^2(u) - 12sin^2(u)]
This is the finite difference of the given equation sin u = sin 3x, expressed in terms of trigonometric functions.
In the given equation, uxx represents the second derivative of the function u(x) with respect to x. The equation is:
uxx * sin(u) = sin(3x)
To find the finite difference, we need to approximate the second derivative using a discrete method. Finite difference is a technique used to approximate derivatives in numerical analysis and can be expressed as:
uxx ≈ (u(x+h) - 2u(x) + u(x-h)) / h^2
Here, h is a small step size. The equation with finite difference becomes:
(u(x+h) - 2u(x) + u(x-h)) / h^2 * sin(u) = sin(3x)
This finite difference equation can be solved for the function u(x) using numerical methods. Note that the exact solution will depend on the boundary conditions and the step size h chosen. In summary, the finite difference method is used to approximate the second derivative in the given trigonometric equation.
To more know about Chain Rule Differentiation Visit:brainly.com/question/28972262
#SPJ11
9. (25 points) Find a unitary matrix U and a diagonal matrix D for which D = U*AU, where A= (III)
Answers
Therefore, the unitary matrix U = [[1, 0, 0], [0, 1, 0], [0, 0, 1]] and the diagonal matrix D = [[1, 0, 0], [0, 1, 0], [0, 0, 1]] satisfy the equation D = UAU^(-1) for the given matrix A = [[1, 0, 0], [0, 1, 0], [0, 0, 1]].
To find a unitary matrix U and a diagonal matrix D such that D = UAU^(-1), where A is the given matrix A = [[1, 0, 0], [0, 1, 0], [0, 0, 1]], we can follow these steps:
Step 1: Find the eigenvalues and eigenvectors of A.
The matrix A = [[1, 0, 0], [0, 1, 0], [0, 0, 1]] is already a diagonal matrix, so its eigenvalues are the diagonal entries, which are 1, 1, and 1. Since the eigenvalues are all equal, we have repeated eigenvalues.
Step 2: Find an orthonormal set of eigenvectors for A.
Since all the eigenvalues are the same, any set of linearly independent vectors can be chosen as eigenvectors. Let's choose the standard basis vectors as the eigenvectors for simplicity:
v₁ = [1, 0, 0]
v₂ = [0, 1, 0]
v₃ = [0, 0, 1]
These vectors are already orthonormal.
Step 3: Construct the unitary matrix U.
The unitary matrix U is constructed by normalizing the eigenvectors. Since the eigenvectors v₁, v₂, v₃ are already orthonormal, we can directly use them as columns of the unitary matrix U: U = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
Step 4: Construct the diagonal matrix D.
The diagonal matrix D is constructed using the eigenvalues of A. Since all the eigenvalues are 1, the diagonal matrix D is simply: D = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
Step 5: Verify D = UAU^(-1).
Let's calculate UAU^(-1) and check if it equals D:
UAU^(-1) = [[1, 0, 0], [0, 1, 0], [0, 0, 1]] * [[1, 0, 0], [0, 1, 0], [0, 0, 1]] * [[1, 0, 0], [0, 1, 0], [0, 0, 1]]^(-1)
= [[1, 0, 0], [0, 1, 0], [0, 0, 1]] * [[1, 0, 0], [0, 1, 0], [0, 0, 1]] * [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
= [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
The result is indeed the diagonal matrix D.
know more about eigenvalue here: brainly.com/question/14415841
#SPJ11
The average weight of a 12 year old boy in the US is 45 kg. If there are 2.2046 pounds in a kg, what is the average weight in pounds? Round your answer to the nearest pound.
Answers
Answer:
X=99
Step-by-step explanation:
1 KG =2.2046 pound
45 KG = x
X=45* 2.2046=99.207
wat iz dis bul crup
i made the hardest math problem, lets see if you can figure it out
p.s. ingore the line right aside from the 7.

Answers
7×(15+7-4+(x+y×38))^3 when x = 4 and y = 9
7×(15+7-4+(4+9×38))^3
=> 7×(15+7-4+(4+342))^3
=> 7×(15+7-4+346)^3
=> 7×364^3
=> 7×48228544
=> 337599808
Help me please, asap

Answers
Answer:
k = \(\frac{1}{3}\)
Step-by-step explanation:
X| 1 2 5 10 30
Y| 3 6 15 30 90
Decide whether the underlined phrase is correct or incorrect as written.
Necesito una bolígrafo.
Answers
Answer:
The phrase Necesito una bolígrafo is correctly written.
Step-by-step explanation:
Necesito una bolígrafo is a spanish phrase
The word for word English Translation is:
Necesito: Need
Una: a
Bolígrafo: Pen
Therefore, the phrase translates to: "I need a pen"
Find the measure of arc AB. Round to the nearest tenth if necessary.

Answers
Answer:
Your answer is 120 degrees.
Step-by-step explanation:
Tina wrote the equations 3 x minus y = 9 and 4 x + y = 5. What can Tina conclude about the solution to this system of equations?
Answers
Answer:
(2, –3) is a solution to the system of linear equations.
Step-by-step explanation:
Given: Equations:
3x - y = 9 --------(1),
4x + y = 5 --------(2),
Add Equation (1) + Equation (2),
3x + 4x = 9 + 5
7x = 14 ( Combine like terms )
x = 2 ( Divide both sides by 7 ),
From equation 1:
3(2) - y = 9
6 - y = 9
-y = 9 - 6 ( Subtraction 6 on both sides )
-y = 3
y = - 3 ( Multiplying -1 on both sides )
Evaluate the following algebraic expression: 2d+200= y=12 a 202 b 202d c 212 d 224
Answers
Answer:
Um there is no y in the equation, only d, so i cant help you im sorry
Step-by-step explanation:
The standard deviation of a numerical data set measures the __________ of the data. Select the most appropriate term that makes the statement true.
A 50th percentile
B average
C most frequent value
D variability
E size
Answers
The standard deviation of a numerical data set measures the variability of the data. It is a widely used measure in statistics that helps to determine how spread out the values are within a given data set.
By calculating the standard deviation, we can better understand the range and distribution of values in the data set, as well as identify potential outliers. This measure is particularly important in fields such as finance, science, and engineering, where understanding the variability in data can be crucial for making informed decisions and predictions. So, the most appropriate term that makes the statement true is D: variability.
To learn more about standard deviation click here
brainly.com/question/23907081
#SPJ11
