can you please solve this in words and mathematical
expressions?
Part D: Knight's Tour (7 marks) How many distinct squares can a chess knight reach after n moves on an infinite chessboard? (The knight's moves are L-shaped: two squares either up, down, left, or righ
Answers
The number of unique squares a knight can reach after n moves on an infinite chessboard is given by the formula (8^n - 1) / 7.
A chess knight makes L-shaped moves, two squares either up, down, left, or right. It can move to any of the eight squares, and the moves can be labeled (±2, ±1) or (±1, ±2), as seen in the diagram below. When the knight moves in an L-shape, it always lands on a square that is a different color than the one it started on.
A knight can't get off the board because it's constantly moving, so it must eventually pass through all of the squares. Since the knight's moves take it to a square of a different color, there are two types of squares on the chessboard: black and white.
We'll label the black squares with a "B" and the white squares with a "W." Because the knight's moves always alternate between colors, the knight can never visit more than half of the squares on the chessboard. Let's assume that the knight begins on a white square (W); it may also begin on a black square (B), but it makes no difference because the squares it can reach in n moves are always the same.
The knight can make eight possible moves from the initial square (W), and each of those moves leads to a different square. The knight can make an additional eight moves from each of those squares. As a result, the number of squares it can reach after n moves is equal to 1 (the original square) + 8 (the squares it can move to after one move) + 8 * 8 (the squares it can move to after two moves) + 8 * 8 * 8 (the squares it can move to after three moves) +...
The formula for the number of squares that a knight can reach in n moves can be written as: 1 + 8 + 8^2 + 8^3 + ... + 8^n-1. This is a geometric series with a common ratio of 8, and the sum of the first n terms of a geometric series is given by the formula: Sn = a(1 - rn) / (1 - r), where a is the first term of the series, r is the common ratio, and n is the number of terms. In this case, a = 1, r = 8, and n = n.
Therefore, the formula becomes: Sn = (1 - 8^n) / (1 - 8). After reducing the formula, we obtain the formula: Sn = (8^n - 1) / 7.The number of unique squares a knight can reach after n moves on an infinite chessboard is given by the formula (8^n - 1) / 7.
For more such questions on chessboard, click on:
https://brainly.com/question/29504883
#SPJ8
Related Questions
If we add, 7xy + 5yz – 3zx, 4yz + 9zx – 4y and –3xz + 5x – 2xy, then the answer is:
A. 5xy+9yz+3zx+5x–4y
B. 5xy+10yz+3zx+15x–4y
C. 5xy–9yz+3zx–5x–4y
D. 5xy+10yz+3zx+5x–6y
Answers
Answer:
A. 5xy + 9yz + 3zx + 5x – 4y
Step-by-step explanation:
uhh credit for this answer goes to Blaise Pascal for inventing calculators .-.
Hewo.
Answer below.
----Steps----
Add the expressions.
5xy+3xz+9yz+5x−4y
Brainliest, if it helps.
3 shapes are combined to form a composite figure. A semicircle is on the bottom, and then a small rectangle connects the semicircle to a triangle.
How can you decompose the composite figure to determine its area?
as three triangles and a circle
as two triangles, a rectangle, and a circle
as a triangle, a pentagon, and a semicircle
as a triangle, a rectangle, and a semicircle3 shapes are combined to form a composite figure. A semicircle is on the bottom, and then a small rectangle connects the semicircle to a triangle.
How can you decompose the composite figure to determine its area?
as three triangles and a circle
as two triangles, a rectangle, and a circle
as a triangle, a pentagon, and a semicircle
as a triangle, a rectangle, and a semicircle
Answers
The composite figure can be decomposed into a triangle, a rectangle, and a semicircle to determine its area.
To decompose the composite figure and determine its area, we can break it down into simpler geometric shapes based on its components. In this case, the composite figure consists of a semicircle, a small rectangle, and a triangle.
We can decompose the figure as a triangle, a rectangle, and a semicircle. Here's how:
Triangle: The upper part of the figure is a triangle. Calculate its area using the formula A = (base * height) / 2, where the base and height are the appropriate measurements.
Rectangle: The small rectangle connects the semicircle to the triangle. Find its area by multiplying the length and width.
Semicircle: The bottom part of the figure is a semicircle. Calculate its area using the formula A = (π * r^2) / 2, where r is the radius of the semicircle.
Once you have determined the areas of each individual shape, add them together to find the total area of the composite figure.
For more questions on triangle
https://brainly.com/question/17335144
#SPJ8
PLEASE HELP ASAP. I WILL GIVE BRAINLIEST!!!
Which of the following is not an expression
A. 7 - 5x
B. 2 + 3x = 8
C. x/2 + 1
D. 2x + 6

Answers
Answer:
B) 2 + 3x = 8
Step-by-step explanation:
Option B is not an expression as expressions do not have equal signs.
approximately how many acres are there in a lot 1/2 mile by 1/2 mile?
Answers
There are approximately 160 acres in a lot that is 1/2 mile by 1/2 mile.
To find the number of acres in a lot, you can use the following formula:
Number of acres = (length in feet) x (width in feet) / 43,560
First, convert the length and width from miles to feet. There are 5,280 feet in a mile, so:
Length in feet = 1/2 mile x 5,280 feet/mile = 2,640 feet
Width in feet = 1/2 mile x 5,280 feet/mile = 2,640 feet
Next, plug these values into the formula:
Number of acres = (2,640 feet) x (2,640 feet) / 43,560 = 174,240,000 / 43,560 = 160 acres
Therefore, there are approximately 160 acres in a lot that is 1/2 mile by 1/2 mile.
Learn more about Acres and Miles here: brainly.com/question/8425742
#SPJ11
A driver descends -15 after 1 minute, -30 feet after 2 minutes and -45 after 3 minutes? If the driver keeps descending at this rate, what is their position after 12 minutes
Answers
Answer:
I think it's -180
Step-by-step explanation:
He keeps descending -15 feet every 1 minute
1 x -15 = -15
2 x -15 = -30
12 x -15 = -180
Ice cream cones cost $1.10 and sundaes cost $2.35. One day, the receipts for a total of 172 cones and sundaes were $294.20. How many cones were sold.
Answers
Answer:88
Step-by-step explanation:
1.10c+2.35s=294.20
C+S=172
1.10c+2.35s=294.20 if you multiply by 100.
110c+235s=29420
-110 (cones + sundaes =172)
-110c-110s=-18920
125s/125=10500/125
S= 84
C+84=172
-84. -84
C= 88
how do you solve | -23.12 + .2361 | + 31.876 ?
Answers
Answer:
54.7599
Step-by-step explanation:
3x - 4y = 10
X + 4y = -21
Answers
ANSWER:
X=-3x-11
Y=3x/4-5/2
Step-by-step explanation:
find the equation in slope-intercept form of the line that passes through the points (-3,4) & (2, -1)

Answers
Answer:
y=-x+`1
Step-by-step explanation:
Just follow the slope-intercept form formula-
Formula: y=mx+b
Key:
y = y-coordinate
m = slope
x = x-coordinate
b = y-intercept
Let me know if you have any questions, hope this helps! (:
Hewwo!
In the figure, O is the centre of the circle , chords MN and RS are intersected at P. If OP is bisector of \( \angle\) MPR , prove that : MN = RS

Answers
Answer:
See Below.
Step-by-step explanation:
Please refer to the diagram below.
We are given that O is the center of the circle, and chords MN and RS are intersected a P. OP is the bisector of ∠MPR. And we want to prove that MN = RS.
We will construct segments OK and OJ such that it perpendicularly bisects MN and RS.
Since OP bisects ∠MPR, it follows that:
\(\displaystyle \angle JPO\cong \angle KPO\)
And since OK and OJ are perpendicular bisectors:
\(m\angle OKP=90^\circ \text{ and } m\angle OJP=90^\circ\)
Therefore:
\(\angle OKP\cong \angle OJP\)
By the Reflexive Property:
\(OP\cong OP\)
Therefore:
\(\Delta OKP\cong \Delta OJP\)
By AAS Congruence.
Hence:
\(OK\cong OJ\)
By CPCTC.
Recall that congruent chords are equidistant from the center.
Thus, by converse, chords that are equidistant from the center are congruent.
Therefore:
\(MN\cong RS\)

Answer:
this is your answer look it once.

can someone please help me

Answers
Answer:
see explanation
Step-by-step explanation:
\(\frac{3\pi }{4}\) is an angle in the second quadrant where sin > 0 and cos < 0
cos(\(\frac{3\pi }{4}\) )
= cos (π - \(\frac{3\pi }{4}\) )
= - cos (\(\frac{\pi }{4}\) )
= - \(\frac{\sqrt{2} }{2}\)
and similarly
sin (\(\frac{3\pi }{4}\) )
= sin (\(\frac{\pi }{4}\) )
= \(\frac{\sqrt{2} }{2}\)
Nolan is following his family's macaroni and cheese recipe. The recipe calls for 6 cups of shredded
cheese and 4 tablespoons of milk. He wants to make a smaller batch, so he uses only 3 cups of
shredded cheese.
How much milk does Nolan need for this smaller batch?
tablespoons
Answers
Answer:2 tablespoons of milk
Step-by-step explanation:
If nolan divides 6 by 2 he gets 3 cups of shredded cheese and to get the same results he would have to divide the milk portion too. 4/2 is 2 so he would need 2 tablespoons of milk.
somebody help me :(
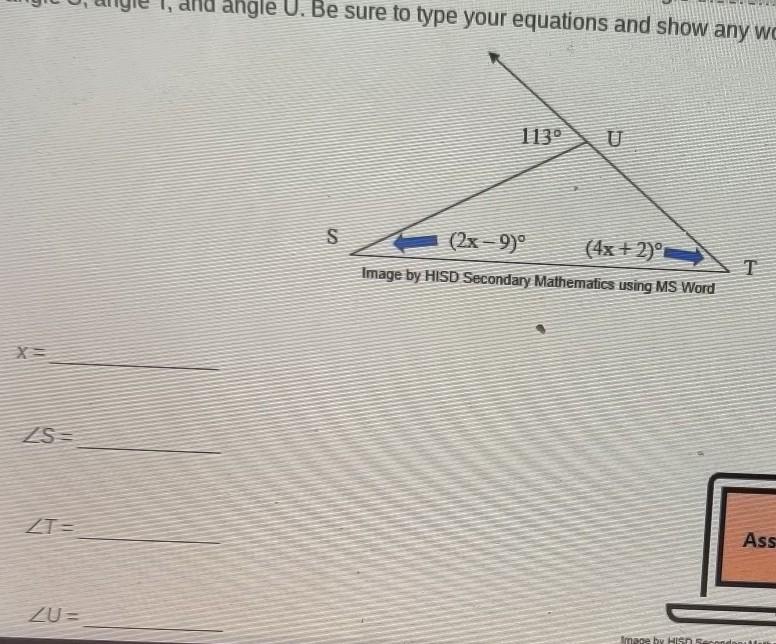
Answers
S= 31
T= 82
U= 67
U = 180 - 113
67 + (2x - 9) + (4x + 2) = 180
6x + 60 = 180
6x = 120
X = 20
Sub 20 for x in equations
S = 2(20) -9 = 31
T = 4(20) + 2 = 82
31 + 82 + 67 = 180
Estimate the sum by rounding each number to the nearest whole number and then adding.
10.6 + 7.067 + 4.78
The sum is approximately

Answers
Answer:
23
Step-by-step explanation:
10.6 > 11
7.067 > 7
4.78 > 5
11+7+5=23
a bowling team consists of 34 members, and 18 are male. if 4 females leave the team, what percent of the remaining members are male?
Answers
Answer:
60%
Step-by-step explanation:
The member of females before they leave the team is 16. If 4 leave the team, then it is 12. Hence, the current amount of members if 30. 18 divided by 30 equals 0.6, which makes 60%.
the stopping distance s of a car varies directly as the square of its speed v. if a car traveling at 30 mph requires 45 ft to stop, find the stopping
Answers
The stopping distance for a car traveling at 55 mph is 60,500 feet.
The equation to solve this problem would look like the following
s = v²/k
The stopping distance s will increase (varies directly) as the velocity increases.
Putting in the values we know
45 = 30²/k
⇒ k = 45/900
⇒ k = 0.05
Now,
at 55 mph we would have
s = 55²/0.05
⇒ s = 3025/0.05
⇒ s = 60,500
s = 60,500 feet to stop
Complete Question:
The stopping distance s of a car varies directly as the square of its speed v. If a car traveling at 30 mph requires 45ft to stop, find the stopping distance for a car traveling at 55 mph.
Learn more about Distance:
https://brainly.com/question/15172156
#SPJ4
I have no idea how to delete a question
This is the anthem
Told the world I need everything and some, yeah
Two girls that's a tandem
She gon' do all it for me when them bands come
Got it all, yeah I'm young, rich, and handsome
Uh, this s is not random
Everybody ain't got it, understand son, yeah
This s is not random
Woah okay
- G easy
Answers
Answer:
you cant
Step-by-step explanation:
good song
solve by system of equations by substitution and show work plz and thank you y=2x+3 y=-x-9
Answers
Answer:
X=-4, y=-5
Step-by-step explanation:
Y=2X+3
y=-x-9
substitute by inserting y value of 2nd equation (-x-9) into y value of 1st equation:
-x-9=2x+3
-x-9+9=2x+3+9
-x=2x+12
-3x=12
x=-4
solve for y by inserting x value (2) into either equation
y=2x+3
y=2(-4)+3
y=-8+3
y=-5
check answer by inserting x and y into either equation to make sure they equal:
y=2x+3
-5=2(-4)+3
-5=-8+3
-5=-5
or
y=-x-9
-5=-(-4)-9
-5=-5
To completely specify the shape of a Normal distribution you must give:
A: the mean and the standard deviation
B: the five number summary
C: the median and the quarties
Answers
A: The mean and the standard deviation.
To completely specify the shape of a Normal distribution, you need to provide the mean and the standard deviation. The mean determines the center or location of the distribution, while the standard deviation controls the spread or variability of the distribution.
The five number summary (minimum, first quartile, median, third quartile, and maximum) is typically used to describe the shape of a distribution, but it is not sufficient to completely specify a Normal distribution. The five number summary is more commonly associated with describing the shape of a skewed or non-Normal distribution.
Similarly, while the median and quartiles provide information about the central tendency and spread of a distribution, they alone do not fully define a Normal distribution. The mean and standard deviation are necessary to completely characterize the Normal distribution.
to know more about deviation visit:
brainly.com/question/31835352
#SPJ11
Solve the following linear programming problem using the simplex method: Minimize: Z = X1 + 2X2 subject to
A. X1+3X2 ≥90
B. 8X1 +2X2 ≥ 160
C. 3X1 +2X2 ≥ 120
D. X2 ≤70
E. X1, X2 ≥ 0
Answers
The answer to the given linear programming problem, which is solved using the simplex method, is as follows:
The optimal solution to minimize the objective function Z = X1 + 2X2 is X1 = 20 and X2 = 0, with the objective function value Z = -100.
To solve the problem, we'll first convert the inequalities to equations by introducing slack and surplus variables. Then we'll set up the initial simplex tableau and iterate through the simplex algorithm until we reach an optimal solution.
⇒ Convert the inequalities to equations:
A. X1 + 3X2 + S1 = 90 (where S1 is the slack variable)
B. 8X1 + 2X2 + S2 = 160 (where S2 is the slack variable)
C. 3X1 + 2X2 + S3 = 120 (where S3 is the slack variable)
D. X2 + S4 = 70 (where S4 is the surplus variable)
⇒ Set up the initial simplex tableau:
| X1 | X2 | S1 | S2 | S3 | S4 | RHS |
----------------------------------------------
Z | -1 | -2 | 0 | 0 | 0 | 0 | 0 |
----------------------------------------------
S1 | 1 | 3 | 1 | 0 | 0 | 0 | 90 |
S2 | 8 | 2 | 0 | 1 | 0 | 0 | 160 |
S3 | 3 | 2 | 0 | 0 | 1 | 0 | 120 |
S4 | 0 | 1 | 0 | 0 | 0 | -1 | 70 |
⇒ a) Select the most negative coefficient in the Z row, which is -2. Choose the corresponding column as the pivot column (X2 column).
b) Find the pivot row by selecting the minimum ratio of the RHS value to the positive values in the pivot column. The minimum ratio is 70/1 = 70. Thus, the pivot row is S4.
c) Perform row operations to make the pivot element (1 in S4 row) equal to 1 and eliminate other elements in the pivot column:
- Divide the pivot row by the pivot element (1/1 = 1).
- Replace other elements in the pivot column using row operations:
- S1 row: S1 = S1 - (1 * S4) = 90 - 70 = 20
- Z row: Z = Z - (2 * S4) = 0 - 2 * 70 = -140
- S2 row: S2 = S2 - (0 * S4) = 160
- S3 row: S3 = S3 - (0 * S4) = 120
d) Update the tableau with the new values:
| X1 | X2 | S1 | S2 | S3 | S4 | RHS |
----------------------------------------------
Z | -1 | 0 | 0 | 0 | 2 | -2 | -140|
----------------------------------------------
S1 | 1 | 3 | 1 | 0 |
0 | 0 | 20 |
S2 | 8 | 2 | 0 | 1 | 0 | 0 | 160 |
S3 | 3 | 2 | 0 | 0 | 1 | 0 | 120 |
S4 | 0 | 1 | 0 | 0 | 0 | -1 | 70 |
e) Repeat steps a to d until all coefficients in the Z row are non-negative.
- Select the most negative coefficient in the Z row, which is -1. Choose the corresponding column as the pivot column (X1 column).
- Find the pivot row by selecting the minimum ratio of the RHS value to the positive values in the pivot column. The minimum ratio is 20/1 = 20. Thus, the pivot row is S1.
- Perform row operations to make the pivot element (1 in S1 row) equal to 1 and eliminate other elements in the pivot column.
- Update the tableau with the new values.
f) The final simplex tableau is:
| X1 | X2 | S1 | S2 | S3 | S4 | RHS |
----------------------------------------------
Z | 0 | 0 | 0 | 0 | 1 | -3 | -100|
----------------------------------------------
X1 | 1 | 3 | 1 | 0 | 0 | 0 | 20 |
S2 | 0 | -22 | -8 | 1 | 0 | 0 | 140 |
S3 | 0 | -7 | -3 | 0 | 1 | 0 | 60 |
S4 | 0 | 1 | 0 | 0 | 0 | -1 | 70 |
⇒ Read the solution from the final tableau:
The optimal solution is X1 = 20 and X2 = 0, with the objective function value Z = -100.
To know more about the simplex method, refer here:
https://brainly.com/question/30387091#
#SPJ11
Manuel is riding his bike. The graph represents the distance Manuel travels from home over time. Distance from home Time I= Describe what is happening as depicted in the graph. Make sure you have at least one sentence describing each segment of the graph.

Answers
Answer: several hours Which is an ordered pair on the line(2.5,14) (2.25,12) (1.25,5) (1.5,9) Jonah's house and his grandparents' house are 8,046.72 meters apart. What is this distance in miles 4 miles 5 miles 7 miles 8 miles
Step-by-step explanation:
The sum of two numbers is 25 one number is 5 less than the other number
Answers
i believe this is right
A property was purchased for $8725.00 down and payments of $1465.00 at the end of every three months for 10 years. Interest is 5% per annum compounded annually. What was the purchase price of the property? How much is the cost of financing? The purchase price of the property was $ (Round the final answer to the nearest cent as needed. Round all intermediate values to six decimal places as needed.) The cost of financing is (Round the final answer to the nearest cent as needed. Round all intermediate values to six decimal places as needed.)
Answers
To calculate the purchase price of the property and the cost of financing, we need to determine the present value of the down payment and the series of payments. Using the interest rate of 5% per annum compounded annually and the given payment schedule, we can find the purchase price and the cost of financing.
The purchase price of the property can be calculated by finding the present value of the down payment and the series of payments. The down payment is $8725.00, which is the initial cash outflow. The payments of $1465.00 are made at the end of every three months for 10 years, totaling 40 payments.
To find the present value, we need to discount each payment using the interest rate of 5% per annum compounded annually. The formula to calculate the present value of a series of payments is:
Present Value = Payment \(\times \left(\frac{1 - (1 + r)^{-n}}{r}\right)\)
where Payment is the periodic payment, r is the interest rate, and n is the total number of payments.
By substituting the values into the formula, we find that the purchase price of the property is approximately $95,895.14.
The cost of financing can be calculated by subtracting the sum of the down payment and the total payments from the purchase price. In this case, the cost of financing is approximately $87,170.14.
Therefore, the purchase price of the property is $95,895.14, and the cost of financing is $87,170.14.
Learn more about interest here:
https://brainly.com/question/14295570
#SPJ11
2/3 (6a+9)
plsss i need it asap
Answers
Answer:
4a +6
Step-by-step explanation:
Simplify the expression
Hope it helps! :)
Please mark me brainliest
Answer:
4a+6
Step-by-step explanation:
To simplify you need to:
2/3(6a+9)=
4a+6
Subtract -7x + 6 from -2x^2 + 9x - 2
Answers
Answer:
\(( - 2 {x}^{2} + 9x - 2) - ( - 7x + 6) \\ = - 2 {x}^{2} + (9 + 7)x + ( - 2 - 6) \\ = - 2 {x}^{2} + 16x - 8\)
which function would be produced by a horizontal stretch of the graph of y = √x followed by a felection in the x-axis
Answers
Answer:
\(y=- \sqrt{\dfrac{1}{2}x}\)
Step-by-step explanation:
Parent functions are the simplest form of a given family of functions.
Transformations of graphs (functions) is the process by which a function is moved or resized to produce a variation of the original (parent) function.
Transformations
\(\begin{aligned} y=f(ax) \implies & f(x) \: \textsf{stretched/compressed horizontally by a factor of} \: a \\ & \textsf{If }a > 1 \textsf{ it is compressed by a factor of}\: a \\ & \textsf{If }0 < a < 1 \textsf{ it is stretched by a factor of}\: a \end{aligned}\)
\(y=-f(x) \implies f(x) \: \textsf{reflected in the} \: x \textsf{-axis}\)
Given parent function:
\(y=\sqrt{x}\)
Horizontal stretch:
As this is a horizontal stretch, the x variable should be multiplied by a value between zero and 1:
\(\implies y= \sqrt{\dfrac{1}{2}x}\)
Reflected in the x-axis:
To reflect a function in the x-axis, simply make the function negative:
\(\implies y=- \sqrt{\dfrac{1}{2}x}\)



Solve the right triangle. Round decimal answers to the nearest tenth

Answers
for me this was the easy way but i belive there are otheres as well
Sorry for bad handwriting
if i was helpful Brainliests my answer ^_^

Select the correct answer.
The manager at a car dealership is tracking the selling prices of two different used car models. When the tracking began, the selling price of
model A was less than $8,000, and the selling price of model B was at most $10,000. The manager has determined that the price of model A is
decreasing at a rate of 12% each year, and the price of model B is decreasing at a rate of 15% each year.
Which system of inequalities can be used to determine after how many years, t, that the selling price, y, will be the same for both car models?
O A.
Ов.
Jy < 8,000(0.88)
y < 10,000(0.85)
Sy < 8,000(1.12)
y < 10,000(1.15)
9 < 8,000(0.88)
y < 10,000(0.85)
Sy < 8,000(1.12)"
1y 10,000(1.15)
Oc.
OD
Answers
Answer:it’s C
Step-by-step explanation:
The system of inequalities can be used to determine, if The selling price of model A was less than $8,000, The selling price of model B was at most $10,000, are x < 8000 × 0.88, and y < 1000 × 0.85.
What is the selling price?The selling price of a good or service is the final cost to the seller, or what the buyer actually pays. A commodity or service in a specific amount, weight, or measurement can be exchanged.
It is one of the most crucial things for a business to decide. It is significant since it determines whether it will survive. Sales of a product are directly impacted by its price.
Given:
The selling price of model A was less than $8,000,
The selling price of model B was at most $10,000,
The price of model A is decreasing at a rate of 12% each year,
The price of model B is decreasing at a rate of 15% each year,
Write the inequality as shown below,
Assume the selling price of A is x,
x < 8000
Assume the selling price of B is y,
y < 1000
The decreased selling price of A,
x < 8000 × (1 - 0.12) = x < 8000 × 0.88
The decreased selling price of B,
y < 1000 × (1 - 0.15) = y < 1000 × 0.85
To know more about the selling price:
https://brainly.com/question/29273267
#SPJ2
In the Acronym WKU, what does each letter represent?
Answers
Answer:
Western Kentucky University
Step-by-step explanation:
Western Kentucky University is a public university in Bowling Green, Kentucky. It was founded by the Commonwealth of Kentucky in 1906, though its roots reach back a quarter-century earlier. It operates regional campuses in Glasgow, Elizabethtown-Fort Knox, and Owensboro.
Answer: Western Kentucky University
Step-by-step explanation:
Use cylindrical or spherical coordinates, whichever seems more appropriate. Evaluate z dV E , where E lies above the paraboloid z
Answers
The resulted integral is \(I=\frac{8}{3} \times \frac{5 \pi}{16}=\frac{5 \pi}{6}\).
What is integrals?In mathematics, an integral is either a number representing the region under a function's graph for a certain interval or just an added to the initial, the derivative of which is initial function (indefinite integral).
Computation of the integrals:
Step 1: We employ the equations in cylindrical coordinates.
\(x=r \cos \theta, y=r \sin \theta, z=z\)
Thus, in cylindrical coordinate system,
E lies above the paraboloid \(z=r^{2}\) and below the plane \(z=2 r \sin \theta\) .
Therefore, the top part E is \(z=2 r \sin \theta\) is the cross-section between paraboloid and the plane.
Now, at the cross-section use, \(r^{2}=2 r \sin \theta\) and \(z=2 r \sin \theta\) .
Thus, the limits are given as ;
\(r^{2} \leq z \leq 2 r \sin \theta \quad 0 \leq r \leq 2 \sin \theta\)
Apply the limits as compute the integration;
\(\begin{aligned}I=\iiint_{E} z d V &=\int_{0}^{\pi} \int_{0}^{2 \sin \theta} \int_{\tau^{2}}^{2 r \sin \theta} z r d r d z d \theta \\&=\int_{0}^{\pi} \int_{0}^{2 \sin \theta}\left[\frac{z^{2}}{2}\right]_{r^{2}}^{2 r \sin \theta} r d r d \theta \\&=\frac{1}{2} \int_{0}^{\pi} \int_{0}^{2 \sin \theta}\left[4 r^{2} \sin ^{2} \theta-r^{4}\right] r d r d \theta\end{aligned}\)
\(\begin{aligned}&=\frac{1}{2} \int_{0}^{\pi} \int_{0}^{2 \sin \theta}\left[4 r^{3} \sin ^{2} \theta-r^{5}\right] d r d \theta \\&=\frac{1}{2} \int_{0}^{\pi}\left[r^{4} \sin ^{2} \theta-\frac{r^{6}}{6}\right]_{0}^{2 \sin \theta} d \theta \\&=\frac{8}{3} \int_{0}^{\pi} \sin ^{6} \theta d \theta\end{aligned}\)
Step 2: Now, calculate for the \(I_{1}=\int_{0}^{\pi} \sin ^{6} \theta d \theta\).
\(\begin{aligned}\sin ^{6} \theta &=\left(\sin ^{2} \theta\right)^{2} \times \sin ^{2} \theta \\&=\left[\frac{1-\cos 2 \theta}{2}\right]^{2} \times\left[\frac{1-\cos 2 \theta}{2}\right] \\&=\frac{1}{8}\left(1-2 \cos 2 \theta+\cos ^{2} 2 \theta\right)(1-2 \cos 2 \theta) \\&=\frac{1}{8}\left(1-2 \cos 2 \theta+\frac{1+\cos 4 \theta}{2}\right)(1-2 \cos 2 \theta)\end{aligned}\)
\(\begin{aligned}&=\frac{1}{16}(3-4 \cos 2 \theta+\cos 4 \theta)(1-2 \cos 2 \theta) \\&=\frac{1}{32}(10-15 \cos 2 \theta+6 \cos 4 \theta-\cos 6 \theta)\end{aligned}\)
Further compute the value of
\(\begin{aligned}I_{1} &=\int_{0}^{\pi} \sin ^{6} \theta d \theta \\&=\frac{1}{32} \int_{0}^{\pi}(10-15 \cos 2 \theta+6 \cos 4 \theta-\cos 6 \theta) d \theta \\&=\frac{1}{32}\left[10 \theta-\frac{15 \sin 2 \theta}{2}+\frac{3 \sin 4 \theta}{2}-\frac{\sin 6 \theta}{6}\right]_{0}^{\pi} \\&=\frac{5 \pi}{16}\end{aligned}\)
Therefore, the obtained integral is \(I=\frac{8}{3} \times \frac{5 \pi}{16}=\frac{5 \pi}{6}\).
Learn more about the indefinite integrals, here
https://brainly.com/question/22008756
#SPJ4
The complete question is -
Use cylindrical or spherical coordinates, whichever seems more appropriate. Evaluate ∫∫∫E z dV, where E lies above the paraboloid
z = x² + y²
and below the plane z = 2y. Use either the Table of Integrals or a computer algebra system to evaluate the integral.