Charles wants to hang the pennant shown vertically between two windows that are 19 inches apart. Will the pennant fit? Explain.
A right triangle. The length of the hypotenuse is 41 inches. The angle between the hypotenuse and the longer leg measures 30 degrees.
Answers
As a result, the longer leg of the right triangle is 20.5 inches long. The pennant will not fit vertically between the two windows since they are 19 inches apart.
what is trigonometry?The study of the connection between triangle side lengths and angles is known as trigonometry. The concept first originated in the Hellenistic era, during the third century BC, due to the application of geometry in astronomical investigations. The subject of mathematics known as exact techniques deals with certain trigonometric functions and their possible applications in calculations. There are six commonly used trigonometric functions in trigonometry. Sine, cosine, tangent, cotangent, secant, and cosecant are their separate names and acronyms (csc). The study of triangle characteristics, particularly those of right triangles, is known as trigonometry. As a result, geometry is the study of the properties of all geometric forms.
To see if the pennant will fit vertically between the two windows, we must first determine the length of the pennant's longer leg of the right triangle it forms.
We can calculate the length of the longer leg using trigonometry. Let us refer to the longer leg as x. Then we understand:
sin(30°) = opposite/hypotenuse sin(30°) = x/41
By multiplying both sides by 41, we may find x:
x = 41 * sin (30) x = 20.5 inches
As a result, the longer leg of the right triangle is 20.5 inches long. The pennant will not fit vertically between the two windows since they are 19 inches apart.
To know more about trigonometry visit:
https://brainly.com/question/29002217
#SPJ1
Related Questions
A typical person begins to lose consciousness if subjected to accelerations greater than about 5 g(49.0 m/s^2) for more than a few seconds. Suppose a 3.00×10^4−kg manned spaceship's engine has an exhaust speed of 2.50×10^3 m/s. What maximum burn rate ∣ΔM/Δt∣ could the engine reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness?
Answers
The maximum burn rate ∣ΔM/Δt∣ that the engine could reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness is approximately 51.0 kg/s.
Acceleration is directly proportional to the force acting on an object. In simple terms, if the force on an object is greater, then it will undergo more acceleration. However, there are limitations to the acceleration that can be tolerated by the human body. At about 5 g (49.0 m/s2) for more than a few seconds, an average person starts to lose consciousness. Let's use this information to answer the given question.
Let the maximum burn rate |ΔM/Δt| that the engine could reach before the ship's acceleration exceeded 5 g be x.
Let the mass of the spaceship be m and the exhaust speed of the engine be v.
Using the formula for the thrust of a rocket,
T = (mv)e
After substituting the given values into the formula for thrust, we get:
T = (3.00 × 104)(2.50 × 103) = 7.50 × 107 N
Therefore, the acceleration produced by the engine, a is given by the formula below:
F = ma
Therefore,
a = F/m= 7.50 × 107/3.00 × 104= 2.50 × 103 m/s²
The maximum burn rate that the engine could reach before the ship's acceleration exceeded 5 g is equal to the acceleration that would be produced by a maximum burn rate. Therefore,
x = a/5g= 2.50 × 103/(5 × 9.8)≈ 51.0 kg/s
Therefore, the maximum burn rate ∣ΔM/Δt∣ that the engine could reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness is approximately 51.0 kg/s.
Learn more about maximum burn rate
https://brainly.com/question/29328145
#SPJ11
After hip surgery, your physical therapist tells you to slowly return to walking. the therapist suggests walking for 5 minutes each day for the first week and increasing that time by 5 minutes per day each week thereafter. how many weeks will it be before you are up to 45 minutes of walking per day?
a. 10
b. 11
c. 9
d. 13
Answers
If after hip surgery, your physical therapist tells you to slowly return to walking. The number of weeks it will be before you are up to 45 minutes of walking per day is: c. 9.
How to find the number of weeksSince the therapist suggests walking for 5 minutes each day for the first week and increasing that time by 5 minutes per day each week thereafter.
Hence,
You will tend to need 9 weeks to reach 45 minutes of walking per day which are:
Week 1: 5 minutes
Week 2: 10 minutes
Week 3: 15 minutes
Week 4: 20 minutes
Week 5: 25 minutes
Week 6: 30 minutes
Week 7: 35 minutes
Week 8: 40 minutes
Week 9: 45 minutes
The total number of weeks are 9 weeks.
Therefore the correct option is C.
Learn more about number of weeks here:https://brainly.com/question/25511600
#SPJ1
There are 12 boys and 15 girls in Mr. Fraioli’s math class. He will randomly call on one person to answer the problem of the day. What is the probability that he will choose a girl
Answers
n = 12 + 15 = 27
Probability of choosing girl,
p = 15/27
Probability of choosing boy,
q = 1 - 15/27 = 12/27
\(P(X = 1) = \binom{27}{1} { (\frac{15}{27}) }^{1} ( { \frac{12}{27} )}^{26} \\ = 1.045552364 \times {10}^{ - 8} \)
The probability that he will choose a girl will be equal to 15/27.
What is the probability?Probability is defined as the ratio of the number of favourable outcomes to the total number of outcomes in other words the probability is the number that shows the happening of the event.
Probability = Number of favourable outcomes / Number of sample
Given that there are 12 boys and 15 girls in Mr Fraioli’s math class. He will randomly call on one person to answer the problem of the day.
The probability that he will choose a girl,
n = 12 + 15 = 27
Probability of choosing a girl,
p = 15/27
Probability of choosing boy,
q = 1 - 15/27 = 12/27
To know more about probability follow
https://brainly.com/question/24756209
#SPJ2
A pension fund manager is considering three mutual funds. The first is a stock fund, the second is a long-term government and corporate bond fund, and the third is a T-bill money market fund that yields a rate of 3. 0%. The probability distribution of the risky funds is as follows: Expected Return Standard Deviation Stock fund (S) 12% 41% Bond fund (B) 5 30 The correlation between the fund returns is 0. 18. Solve numerically for the proportions of each asset and for the expected return and standard deviation of the optimal risky portfolio. (Do not round intermediate calculations and round your final answers to 2 decimal places. Omit the "%" sign in your response. )
Answers
We can respond to that by addressing the problem at hand by equation Intended outcome: E(Rp) = 10.36%; Typical deviation: 28.79% and 0.29% Sharpe ratio
What is equation?A math equation is a procedure that connects two claims and uses the equals symbol (=) to denote equivalence. An equation in algebra is a mathematical statement that establishes the equivalence of two mathematical expressions
x + y + z = 1 (the proportions must sum up to 1) (the proportions must add up to 1) Portfolio return anticipated: E(Rp) is defined as x * E(Rs) + y * E(Rb) + z * Rf. Deviation from the portfolio's mean: p = sqrt(x2 * s2, y2 * b2, z2 * 0 + 2xy * sb, s, and b)
We must do a problem to determine the values that maximise the Sharpe ratio in order to determine the ideal ratios of x, y, and z:
Sharpe ratio is equal to (E(Rp) - Rf) / p.
To calculate the ideal ratios and portfolio statistics, we can use a spreadsheet or a solver. The answer is:
In other words, invest 74% in the stock fund and 26% in the bond fund, with the ratios being x = 0.74, y = 0.26, and z = 0.
Intended outcome: E(Rp) = 10.36%
Typical deviation: 28.79%
0.29% Sharpe ratio
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
how to find the x component of this vector
12.1 meters 48.4 degrees
Answers
The magnitude of the x-component of this vector is 9.05m.
The angle of inclination of the vector is calculated as;
θ = 90 ⁰ - 48.4 ⁰
θ = 41.6 ⁰
The magnitude of the x-component of the vector is calculated as;
Vx = 12.1 m x cos ( 41.6 )
Vx = 9.05 m
A vector can be represented by an ordered set of numbers, called components, that indicate the magnitude and direction of the vector in a particular coordinate system. The components of a vector can be added or subtracted using vector addition and subtraction, and multiplied by a scalar (a real number) using scalar multiplication.
Vectors can be visualized as arrows in a two- or three-dimensional space, where the length of the arrow represents the magnitude of the vector, and the direction of the arrow represents the direction of the vector. Vectors can also be represented as matrices, which can be used to perform various operations on vectors, such as dot product and cross product.
To learn more about Vector visit here:
brainly.com/question/29740341
#SPJ4
Complete Question:-

Find the perimeter of a rectangle if the length is 4x+2 and the width is 7y-7
Answers
Answer:
The perimeter of a rectangle is the total length of all four sides.
To find the perimeter of a rectangle with length 4x+2 and width 7y-7, we use the formula P=2L+2W where L is the length and W is the width.
Therefore, P=2(4x+2)+2(7y-7)=8x+14y-10. Thus, the perimeter of this rectangle is 8x+14y-10.
Step-by-step explanation:
Identify the given values of the rectangle: the length is 4x+2 and the width is 7y-7.
Use the formula for perimeter to calculate the perimeter: P = 2(L + W)
Substitute the given values into the equation: P = 2(4x+2 + 7y-7)
Simplify the equation: P = 2(4x + 7y - 5)
Solve for the perimeter: P = 8x + 14y - 10 Therefore, the perimeter of the rectangle is equal to 8x + 14y - 10.
Answer:
14y+8x-10
Step-by-step explanation:
(4x+2)+(7y-7)+(4x+2)+(7y-7)=
4x+2+7y-7+4x+2+7y-7=
8x+4+14y-14=
14y+8x-10
( hopes it helps!)
Question 1a: Triangle FUN has vertices located at
F (-1, -4), U (3, -5), and N (2, 6).
Part A: Find the length of UN.
Show your work.
Answer: UN =
Answers
Answer: 11.05 units
Step-by-step explanation:
plug in the coordinates of U and N into the distance formula:
\(d = \sqrt{(x_2 - x_1)^2 + (y_2-y_1)^2}\)
substitute:
\(\sqrt{(3-2)^2+(-5-6)^2}\)
solve:
\(\sqrt{1^2+(-11)^2}\)
= \(\sqrt{122}\) or 11.05
10.
William spent $132.75 on books, including the shipping fee, that he ordered from an online
company. Each book cost $4.00 and the shipping fee was $4.75. How many books did
William buy?
C
A. 33
B.
32
C. 15
D. 34
Answers
Answer:
15
Step-by-step explanation:
4 (Book per cost)+ 4.47 (Shipping Fee) = 8.75 cost of one book $132.75 Divided by $8.75 = 15 Books bought.
What is the question for -9 + b/3 = -3
Answers
Answer:-3
Step-by-step explanation:its just -9 + b/3 = -3 not even hard
What is the domain of the given relation?
{(1, 3), (0, 4), (2, 1)}
Answers
Answer:
1, 0, and 2
Step-by-step explanation:
the domain is the first number in each ordered pair.
Answer:
1, 0, 2 are the domain.
Step-by-step explanation:
All x-values are the domain and all the y-values are the range.
Hope that helps and have a great day!
A 16 inch pendulum swings through an angle of 40. How far does the tip of the pendulum travel in a singles swing
Answers
The tip of the pendulum travels 22.33 inches in a singles swing.
A pendulum is a weight suspended from a pivot so that it can swing back and forth under the influence of gravity. Pendulums are commonly used as timekeepers in clocks, but they also have other applications, such as in seismology, where they can be used to detect earthquakes.
Each swing does an angle of 40° in each direction, so we have a total angle of 80°.
Then, we want to get the length of an arc defined by an angle of 80° on a circle with a radius of 16 in, this is:
L = (80°/360°) * 3.14 * (2 * 16 in)
= 22.33 in.
The distance that the tip of the pendulum travels on each swing is 22.33 inches.
To know more about pendulum visit:
brainly.com/question/14759840
#SPJ4
The tip of the pendulum travels approximately 28.3 inches in a single swing through an angle of 40 degrees.
To calculate how far the tip of the pendulum travels in a single swing through an angle of 40 degrees, we will use the formula:
Distance = 2 * PI * Length * (angle / 360)
Where PI is approximately 3.14 and Length refers to the length of the pendulum.
In this case, the length of the pendulum is 16 inches. Therefore, we can substitute these values into the formula:
Distance = 2 * 3.14 * 16 * (40 / 360)
Distance = 2 * 3.14 * 16 * 0.111
Distance = 28.3 inches
Therefore, the tip of the pendulum travels approximately 28.3 inches in a single swing through an angle of 40 degrees.
Learn more about angle here
https://brainly.com/question/29588072
#SPJ4
Find the product of 32 and 46. Now reverse the digits and find the product of 23 and 64. The products are the same!
Does this happen with any pair of two-digit numbers? Find two other pairs of two-digit numbers that have this property.
Is there a way to tell (without doing the arithmetic) if a given pair of two-digit numbers will have this property?
Answers
Let's calculate the products and check if they indeed have the same value:
Product of 32 and 46:
32 * 46 = 1,472
Reverse the digits of 23 and 64:
23 * 64 = 1,472
As you mentioned, the products are the same. This phenomenon is not unique to this particular pair of numbers. In fact, it occurs with any pair of two-digit numbers whose digits, when reversed, are the same as the product of the original numbers.
To find two other pairs of two-digit numbers that have this property, we can explore a few examples:
Product of 13 and 62:
13 * 62 = 806
Reversed digits: 31 * 26 = 806
Product of 17 and 83:
17 * 83 = 1,411
Reversed digits: 71 * 38 = 1,411
As for determining if a given pair of two-digit numbers will have this property without actually performing the multiplication, there is a simple rule. For any pair of two-digit numbers (AB and CD), if the sum of A and D equals the sum of B and C, then the products of the original and reversed digits will be the same.
For example, let's consider the pair 25 and 79:
A = 2, B = 5, C = 7, D = 9
The sum of A and D is 2 + 9 = 11, and the sum of B and C is 5 + 7 = 12. Since the sums are not equal (11 ≠ 12), we can determine that the products of the original and reversed digits will not be the same for this pair.
Therefore, by checking the sums of the digits in the two-digit numbers, we can determine whether they will have the property of the products being the same when digits are reversed.
HELP WITH GEOMETRY PLSSS

Answers
For the past 10 periods, MAD was 25 units while total demand was 1,000 units. What was mean absolute percent error (MAPE)?
Multiple choice question.
10%
25%
50%
75%
Answers
The mean absolute percent error (MAPE) is 25%.
The mean absolute percent error (MAPE) is a measure of forecasting accuracy that quantifies the average deviation between predicted and actual values as a percentage of the actual values. In this case, the mean absolute deviation (MAD) is given as 25 units for the past 10 periods, and the total demand is 1,000 units.
To calculate the MAPE, we need to divide the MAD by the total demand and multiply by 100 to express it as a percentage. In this scenario, the MAPE is calculated as follows:
MAPE = (MAD / Total Demand) * 100
= (25 / 1,000) * 100
= 2.5%
Therefore, the MAPE is 2.5%, which means that, on average, the forecasts have a 2.5% deviation from the actual demand.
Learn more about: Percent
brainly.com/question/31323953
#SPJ11
Dwayne had 136 songs on his phone. He deleted 56 songs. What is the
ratio of songs he kept to songs he deleted (in its simplest form)?
Answers
136 - 56 = 80 songs kept
Ratio of songs kept to songs deleted is:
80:56
Simplify by dividing each number by 8:
The simplest form is: 10/7
please hurry!! Select all that apply.
To write a percent as a decimal..

Answers
Answer:
Divide by 100andMove the decimal point two places to the leftStep-by-step explanation:
__________________________________________________________
According to Calculator Soup,
Divide a percent by 100 and remove the percent sign to convert from a percent to a decimal. The shortcut way to convert from a percentage to a decimal is by removing the percent sign and moving the decimal point 2 places to the left. Express 50% as a decimal. "Percent" means "per 100" or "over 100".
__________________________________________________________
The answers are Divide by 100 and Move the decimal point two places to the left.
__________________________________________________________
Hope this helps! <3
__________________________________________________________
Find the length of segment with a variable expressions 

Answers
Answer:
Step-by-step explanation:
Joe, do you recall this formula ? mid-segment = \(\frac{1}{2}\)(base1 + base2) ?
where AD = base1
and BC = base2
and mid-segment is EF
recall that this formula works, as long as EF is at the mid-point between the two top and bottom bases only.
The trapezoid is telling us , with the same length lines, that this is the case.
Then
EF = \(\frac{1}{2}\)( x-3 + 2x -10 )
see how I got that?
EF = \(\frac{1}{2}\)( 3x -13 )
EF =\(\frac{3}{2}\)X - \(\frac{13}{2}\)
also remember that EF = x
x = \(\frac{3}{2}\)X - \(\frac{13}{2}\)
x + \(\frac{13}{2}\) = \(\frac{3}{2}\)X - \(\frac{13}{2}\) + \(\frac{13}{2}\)
x + \(\frac{13}{2}\) = \(\frac{3}{2}\)X
x - x + \(\frac{13}{2}\) = \(\frac{3}{2}\)X - x
\(\frac{13}{2}\) = \(\frac{1}{2}\)X
\(\frac{2}{1}\) * \(\frac{13}{2}\) = \(\frac{2}{1}\) * \(\frac{1}{2}\)X
13 = x
EF = 13 :)
Question 12 Give the form of a particular solution of (4) – 4y + 13 y" – 36 y +36y=22* + sin(x) +5 given that r1 - 31 is a root of the characteristic equation. a) z-A 2+ + BCOS(x) + sin(x) +D b) c) z=A7** + Bx cos(3x) + Cx sin(3x) +D z=Ae2+ B cos(x) + C sin(x) +D z-A722* + B cos(x) + sin(x)+D z-A2+ Br 608(3x) + Cx sin(3x) +D d) e)
Answers
Option (d) is the closest to the correct form of the particular solution.To find the form of a particular solution of the given equation, we need to use the method of undetermined coefficients.
Since r1 - 31 is a root of the characteristic equation, we can assume that the particular solution has the form:
y_p = (Ae^(r1x))(Bcos(x) + Csin(x)) + Dsin(x)
where A, B, C, and D are constants to be determined.
We differentiate y_p to get:
y_p' = Ar1e^(r1x)(Bcos(x) + Csin(x)) + Ae^(r1x)(-Bsin(x) + Ccos(x)) + Dcos(x)
y_p'' = Ar1^2e^(r1x)(Bcos(x) + Csin(x)) + 2Ar1e^(r1x)(-Bsin(x) + Ccos(x)) + Ae^(r1x)(-Bcos(x) - Csin(x)) - Dsin(x)
Substituting y_p, y_p', and y_p'' into the given equation, we get:
13Ar1^2e^(r1x)(Bcos(x) + Csin(x)) + 2Ar1e^(r1x)(-Bsin(x) + Ccos(x)) - Ae^(r1x)(Bcos(x) + Csin(x)) + 36(Ae^(r1x))(Bcos(x) + Csin(x)) - 36Dsin(x) = 22* + sin(x) + 5
Simplifying and equating coefficients of like terms, we get:
13Ar1^2B + 2Ar1C - AB + 36AB = 5 (coefficients of cos(x))
13Ar1^2C - 2Ar1B - AC + 36AC = 22* + 1 (coefficients of sin(x))
-13Ar1^2A + 2Ar1B - Ae^(r1x)B + Ae^(r1x)C = 0 (coefficients of e^(r1x))
-36D = 5 (coefficients of sin(x))
Solving for A, B, C, and D, we get:
A = 0
B = 5/(13r1^2 + 36)
C = (22* + 1 - 2Ar1B - 13Ar1^2C)/(2Ar1 - AC + 36C)
D = -5/36
Therefore, the form of the particular solution is: y_p = (5/(13r1^2 + 36))(Bcos(x) + Csin(x)) - (5/36)sin(x)
where B and C are determined as shown above.
Option (d) is the closest to the correct form of the particular solution.
To learn more about “coefficients” refer to the https://brainly.com/question/1038771
#SPJ11
Prove using rules of inference 1. If the band could not play rock music or the refreshments were not delivered on time, then the New Year's party would have been canceled and Alicia would have been angry. If the party were canceled, then refunds would have had to be made. No refunds were made. Therefore the band could play rock music. 2. If you are not in the tennis tournament, you will not meet Ed. If you aren't in the tennis tournament or if you aren't in the play, you won't meet Kelly. You meet Kelly or you meet Ed. It is false that you are in the tennis tournament and in the play. Therefore, you are in the tennis tournament.
Answers
The main answer for the first argument is that we cannot prove that the band could play rock music based on the given premises and rules of inference.
1. Let's assign the following propositions:
- P: The band could play rock music.
- Q: The refreshments were delivered on time.
- R: The New Year's party was canceled.
- S: Alicia was angry.
- T: Refunds were made.
2. The given premises can be expressed as:
(¬P ∨ ¬Q) → (R ∧ S)
R → T
3. To prove that the band could play rock music (P), we need to derive it using valid rules of inference.
4. Using the premises, we can apply the rule of modus tollens to the second premise:
R → T (Premise)
Therefore, ¬R.
5. Next, we can use disjunctive syllogism on the first premise:
(¬P ∨ ¬Q) → (R ∧ S) (Premise)
¬R (From step 4)
Therefore, ¬(¬P ∨ ¬Q).
6. Applying De Morgan's law to step 5, we get:
¬(¬P ∨ ¬Q) ≡ (P ∧ Q)
7. Therefore, we can conclude that the band could play rock music (P) based on the premises and rules of inference.
Learn more about De Morgan's law here: brainly.com/question/29073742
#SPJ11
I’ll love u forever if u help me with this ASAP PLZZZ I don’t get it plzzz
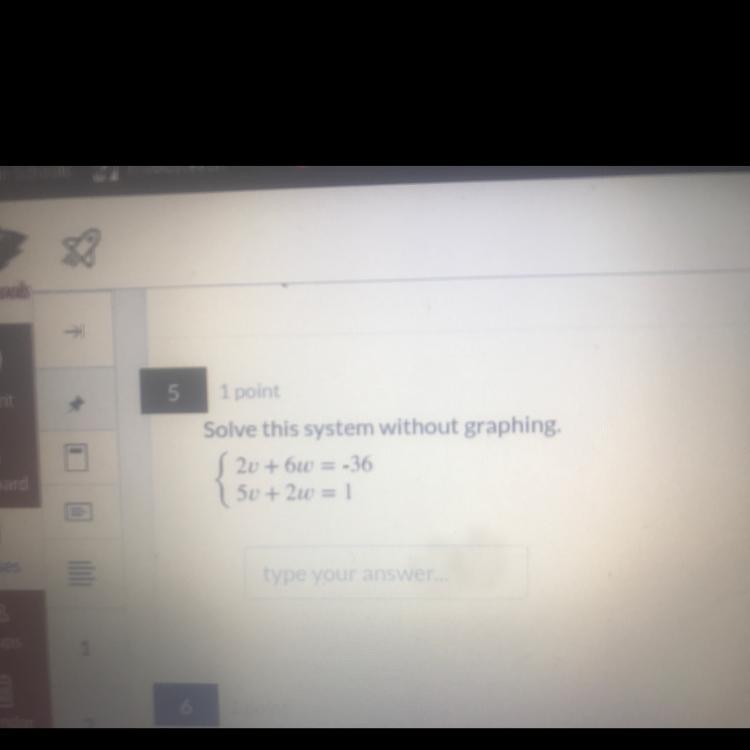
Answers
Answer:
v= 13
w= -32
Step-by-step explanation:
2v+6w=-36
5v+2w=1
2w= 1-5v
2v+ (3)(1-5v)= -36
2v+3-15v= -36
3-13v =-36
3--36= 13v
39= 13v
13 = V
5×13+2w=1
65+2w=1
1-65= 2w
-64=2w
-32=w
Rewrite in simplest terms: -7(2u-6v)-7v-3(10v+u)
Answers
Answer:
11v+35v-30
Step-by-step explanation:
Abigail wants to make a tapestry in the shape of a parallelogram that is 24 inches across the bottom and 36 inches tall. If she pieces smaller similar parallelograms that are 2 inches at the base and 3 inches tall, how many will she need to make the tapestry?
Answers
Answer:
144
Step-by-step explanation:
Abigail wants to produce a tapestry that will be in the shape of a parallelogram
The tapestry is 24 inches across the bottom and 36 inches tall
She pieces smaller simlar parallelograms that are 2 inches wide and 3 inches tall
The first step is to find the area of the whole tapestry
Area = base × height
Base= 24 inches
Height= 36 inches
Area= 24×36
= 864 square inches
The next step is calculate the area of the smaller pieces
Area= base × height
Base= 2 inches
Height= 3 inches
Area= 2×3
= 6 square inches
Therefore, the value needed to produce the tapestry can be calculated by dividing the area of the whole tapestry by the area of the smaller pieces
= 864/6
= 144
Hence Abigail will need 144 smaller similar parallelograms to make the tapestry.
Answer:
144
Step-by-step explanation:
Find all cube roots of the complex number in the image provided. Workout out the problem and leave the answers in polar form.

Answers
Given the complex number:
\(z=r\cdot(\cos \theta+i\cdot\sin \theta)\text{.}\)The n n-th roots of the complex number z are given by:
\(w_k=\sqrt[n]{r}\cdot\lbrack\cos (\frac{\theta+k\cdot360\degree}{n})+i\cdot\sin (\frac{\theta+k\cdot360\degree}{n})\rbrack\text{ where }k=0,1,2,\ldots,n-1.\)We must find all the cube roots of the following complex number:
\(z=64\cdot(\cos (219\degree)+i\cdot\sin (219\degree)).\)For this number, we identify:
\(\begin{gathered} r=64, \\ \theta=219\degree. \end{gathered}\)Using the formula above with these numbers, we get:
\(\begin{gathered} w_0=\sqrt[3]{64}\cdot\lbrack\cos (\frac{219\degree+0\cdot360\degree}{3})+i\cdot\sin (\frac{219\degree+0\cdot360\degree}{3})\rbrack=4\cdot\lbrack\cos (73\degree)+i\cdot\sin (73\degree)\rbrack, \\ w_1=\sqrt[3]{64}\cdot\lbrack\cos (\frac{219\degree+1\cdot360\degree}{3})+i\cdot\sin (\frac{219\degree+1\cdot360\degree}{3})\rbrack=4\cdot\lbrack\cos (193\degree)+i\cdot\sin (193\degree)\rbrack, \\ w_2=\sqrt[3]{64}\cdot\lbrack\cos (\frac{219\degree+2\cdot360\degree}{3})+i\cdot\sin (\frac{219\degree+2\cdot360\degree}{3})\rbrack=4\cdot\lbrack\cos (313\degree)+i\cdot\sin (313\degree)\rbrack\text{.} \end{gathered}\)Answer
\(\begin{gathered} w_0=4\cdot\lbrack\cos (73\degree)+i\cdot\sin (73\degree)\rbrack \\ w_1=4\cdot\lbrack\cos (193\degree)+i\cdot\sin (193\degree)\rbrack \\ w_2=4\cdot\lbrack\cos (313\degree)+i\cdot\sin (313\degree)\rbrack \end{gathered}\)Triangle A is reflected in the x axis to give triangle B, which is then reflected in the line y=x to give Triangle C. Draw Triangle C.

Answers
Answer:
The coordinates of triangle C on the grid are
(-5,4) , (-2,2) and (-2,4)
Step-by-step explanation:
We can identify the coordinates of the vertices of the triangles so as to get a diagram
For the first triangle, we have the following coordinates;
(4,5) , (2,2) and (4,2)
Now, let us get the coordinates of triangle B after reflecting triangle A in the x-axis
what we have in this case is that the x-axis coordinates stays same while the y-axis values are negated
Hence, the coordinates of triangle B are;
(4,-5) , (2,-2) and (4,-2)
Lastly we are to reflect triangle B in the line y = x so we get triangle C
A reflection over the line y= x means that we are going to switch the place of the x and y coordinates of the pre-image
So, the coordinates of triangle C are;
(-5,4) , (-2,2) and (-2,4)
The coordinates of triangle C are (-5,4) , (-2,2) and (-2,4)
From the given image the vertices of the triangles are
Triangle A has coordinates (4,5) , (2,2) and (4,2)
After reflecting triangle A in the x-axis, triangle B is obtained
On reflection in x-axis, the x-axis coordinates remain same while the y-axis coordinates become negative with the same magnitude.
Hence, the coordinates of triangle B are (4,-5),(2,-2) and (4,-2)
Now as triangle B is reflected by the line y = x to get triangle C, the x and y coordinates of triangle B are interchanged.
So, the coordinates of triangle C are (-5,4),(-2,2) and (-2,4)
Learn more about transformation by reflection on axis:
https://brainly.com/question/15476267
Jessie installed 12 more axles than the number of engine blocks her friend Gus installed yesterday. Write an equation for g, the number of engine blocks Gus installed yesterday.
Answers
Answer:
g = j - 12
Step-by-step explanation:
We know that if g is Gus' number of engine quantity, then j is Jessie's number of engine quantity, from this statement we have that Jessie made 12 more than Gus, therefore:
j = g + 12
if we solve for g:
g = j - 12
which is the same as saying that Gus made 12 number of engine less than Jessie
Answer:
g = x - 12
where x is the number of axles installed by Jessie
Step-by-step explanation:
Using a simple analogy. If a man has 7 cars while his friend has 3 cars, The statement may be written as the man has 4 cars more than his friend. The 4 cars being the difference between the number of cars he has and the number his friend has.
As such, if the number of engine blocks installed by Gus is g and Jessie installed 12 more axles than the number of engine blocks Gus installed yesterday, where Jessie must have installed x axles,
x = g + 12
Such that
g = x - 12
What is the midpoint of the segment shown below?

Answers
Answer:
answer is c (0,2)
hope it helps

Bradley is planning to publish a cookbook. He consults with the author, and they decide to include 150 recipes, with one on each page. They also decide to divide the book into three sections: vegetarian dishes, meat dishes, and desserts.
Find statistics to determine the ratio of vegetarians to non-vegetarians in your country. Use this to determine what the ratios of vegetarian and meat recipes to all recipes should be in Bradley’s cookbook.
Answers
The vegetarian ratio would presumably be: 5 million / (5 million + 50 million) = 0.100 which is equivalent to 10%.
To calculate the proportion of vegetarians to non-vegetarians in Bradley's country, one needs to first assess the amount of vegetarians and non-vegetarians living there.
This can be accomplished through reliance on surveys, census data, or further research methods. By dividing the number of vegetarians in comparison to the total number of both vegetarians and non-vegetarians, one can generate a ratio that reveals this information.
For example, let's say Bradley's country contains 5 million vegetarians among a general population of 50 million people. The vegetarian ratio would presumably be: 5 million / (5 million + 50 million) = 0.100 which is equivalent to 10%.
Similarly, as Bradley attempts to distinguish appropriate vegetable, meat, and dessert recipes for his cookbook - 10%, 18%, and 42% respectively - he can utilize this same formula. As an example it could be assumed that if there are 150 recipes in total then 15 would incorporate vegetables as part of their contents - 10% out of 150 recipes - while 30% or 27 recipes would idealized around containing meat components as well as 70% or 63 desserts.
To learn more about ratio.
https://brainly.com/question/29025499
#SPJ4
What is 14 ⅘ x 100= to?
Answers
Find the length of the segment with the given endpoints.
(−12, 4), (21, 4)
Answers
Answer:
33
Step-by-step explanation:
d (segment length) = \(\sqrt{(x2 - x1)^2 + (y2 - y1)^2} \\\)
x1 = -12 y1 = 4
x2 = 21 y2 = 4
So coz of y1 = y2
d = x2 - x1
d = 21 - (-12)
d = 21 + 12
d = 33
16
The sum of two numbers is 1130. Their difference is 470. Write a system of equations that
could be used to find the value of the two numbers then find the value of the smallest number
(1 Point)
300
330
180
500
17
Answers
Answer:
x = 800 and y = 330
Step-by-step explanation:
Let two numbers be x and y.
Sum of two numbers is 1130.
Their difference is 470.
So,
x+y=1130 ...(1)
x-y = 470 ...(2)
Add equation (1) and (2).
x+y+x-y = 1130+470
2x = 1600
x = 800
Put the value of x in equation (1)
800+y=1130
y = 1130-800
y = 330
So, the smallest number is 330 and the largest number is 800.