Charmaine sells beaded necklaces. Each large necklace sells for $5.80 and each small necklace sells for $4.80. How much will she earn from selling 4 large
necklaces and 1 small necklace?
Answers
Related Questions
с
6.5
D
2.6
ө
A
4.9
В
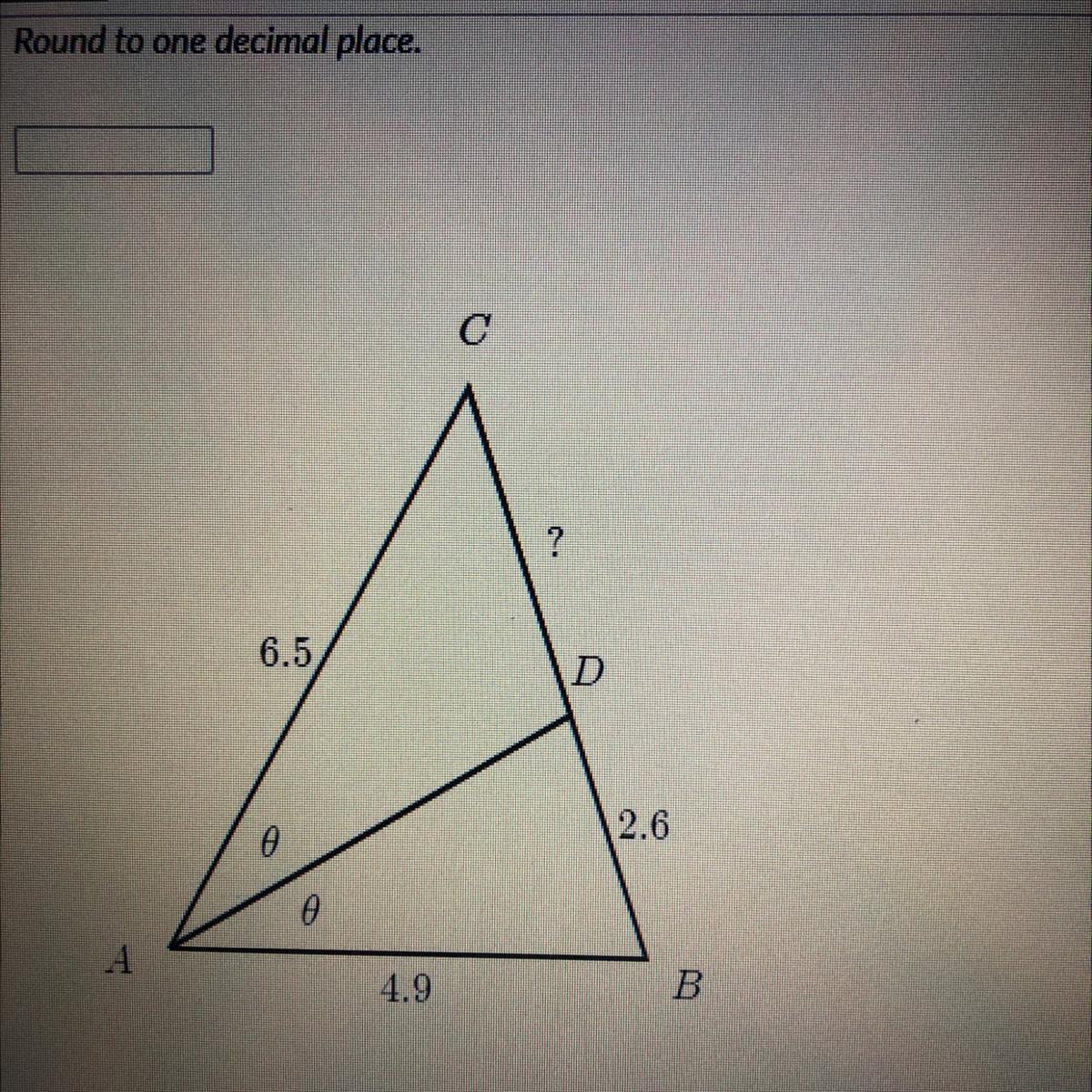
Answers
Answer:
i think
the answer is A. 4.9
Explain how to determine whether $20 is the correct estimate of the product of \$5.68(4.1)

Answers
Answer:
No, it will not be enough.
Step-by-step explanation:
Hello!
This estimation is incorrect, as 5.68 would round up to 6, and 4.1 would round down to 4.
Multiplying them both will give us 24, which can be justified as the actual product is 23.29.
Therefore the estimation of $20 will not be enough for 4.1 pounds of cherries.
find the first four terms of the sequence given by the following

Answers
Answer:
42, 38, 34, 30
Step-by-step explanation:
You want the first 4 terms of the sequence described by ...
an = 42 -4(n -1), n ∈ ℕ
Arithmetic sequenceYou can write the first 4 terms of the sequence by evaluating the 'an' expression for n = 1, 2, 3, 4.
Or, you can recognize the expression describes a sequence with a first term of 42 and a common difference of -4. That is, each term is 4 less than the one before.
The terms you want are ...
42, 38, 34, 30
__
Additional comment
The equation for the n-th term of an arithmetic sequence is ...
an = a1 +d(n -1)
where a1 is the first term, and d is the common difference. Comparing this to the given equation, we see a1 = 42, d = -4.
<95141404393>

Which is the equation of the graphed line written in standard form? y = x x – x minus StartFraction one-half EndFraction y equals 0.y = 0 x – y = 0 y = y equals StartFraction one-half EndFraction x.x
Answers
Answer:
its is C. X-Y= 0
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
plz let me know if this is incorrect
what is the equation of line a
what is the equation of line b
i have no clue so some one help

Answers
the marks on a statistics midterm test are normally distributed with a mean of 78 and a standard deviation of 6. what is the probability that a class of 36 has an average midterm mark that is more than 77.83?
Answers
The probability that a class of 36 has an average midterm mark that is more than 77.83 is 0.0766. This is because the mean of the normally distributed marks is 78 and the standard deviation is 6. Using the standard normal distribution formula, we can calculate the probability that the average mark of 36 students is more than 77.83.
Standard Normal Distribution Formula: P(x > a) = 1 - P(x < a)
P(x > 77.83) = 1 - P(x < 77.83)
P(x > 77.83) = 1 - 0.9234
P(x > 77.83) = 0.0766
What is the margin of sampling error if p=16% and n=400?Formula : ME=2 √p(1-p)/nOptions : 1- about 2% 2- 3% 3- 4% 4- 5%5- 6%
Answers
Given:
p = 16%
and, n = 400
We will find the margin of sampling error
The formula to find the margin of sampling error will be:
\(ME=2\sqrt[]{\frac{p(1-p)}{n}}\)substitute with (p) and (n):
\(ME=2\sqrt[]{\frac{0.16\cdot(1-0.16)}{400}}=0.03666\cdot100\%=3.666\%\)Rounding to the nearest whole percent
So, the answer will be 4%
What is the volume of this rectangular prism?

Answers
Answer:
20
Step-by-step explanation:
volume: lwh
.666*5*6=20
Answer:
20 cm³
Step-by-step explanation:
\(\frac{2}{3}\) · 6 · 5
\(\frac{2}{3}\) · 30
20 cm³
In large restaurant an average of3 out every 5 customers ask water with their meal. Random sample of 10 customers were selected. What is the probability that exactly 6patients at least 2 patients
Answers
The probability that exactly 6 patients is 2.0669, and the probability that at least 2 patients is 0.0017.
In large restaurants, an average of 3 out of every 5 customers ask for water with their meal. A random sample of 10 customers was selected. We need to estimate the probability that exactly 6 patients and at least 2 patients. The given situation is a binomial distribution since the experiment has only two outcomes, success or failure.
Here, Success is defined as requesting water with a meal, and failure as not requesting water with a meal. The probability of success is p = 3/5 = 0.6 and the probability of failure is q = 1 - p = 1 - 0.6 = 0.4. Let X be the number of patients requesting water with a meal out of 10 patients selected.
P(X = 6) = 10C6 (0.6) (0.4)⁴
= 210 × 0.31104 × 0.0256
= 2.0669P(X ≥ 2)
= P(X = 2) + P(X = 3) + .... + P(X = 10)P(X ≥ 2)
= 10C2 (0.6)² (0.4)⁸ + 10C3 (0.6)³ (0.4)⁷ + ..... + 10C10 (0.6)¹⁰ (0.4)⁰ P(X ≥ 2)
= 0.0022 + 0.0185 + 0.0881 + 0.2353 + 0.3454 + 0.2508 + 0.0986 + 0.0180 + 0.0016P(X ≥ 2)
= 1 - P(X < 2)P(X < 2) = P(X = 0) + P(X = 1)P(X < 2)
= 10C0 (0.6)⁰ (0.4)¹⁰ + 10C1 (0.6)¹ (0.4)⁹ P(X < 2)
= 0.0001 + 0.0016P(X < 2)
= 0.0017
You can learn more about probability at: brainly.com/question/31828911
#SPJ11
0,7 as common fraction
Answers
Answer:
Sure! A common fraction would be 7/10, because it is the simplest form that we can have of .7 in a fraction form.
on a certain island there are two populations of deer. after years, the numbers of deer in the two populations are and . when is the total population smallest?
Answers
On a certain island there are two populations of deer. after years, the numbers of deer in the two populations is zero.
Let x be the population of the first group of deer and y be the population of the second group of deer.
The total population is given by x + y.
The numbers of deer in the two populations are x and y.
Suppose that the population of the first group increases at a rate of a per year, and the population of the second group increases at a rate of b per year.
Then the differential equations that describe the growth of the populations are as follows:
dx/dt = ax
dy/dt = by
The solution to these equations is
\(x(t) = x_0ert\\ y(t) = y_0ert\)
where \(x_0 \:and \: y_0\) are the initial populations of the first and second groups of deer, respectively.
The total population P(t) at time t is given by
\(P(t) = x(t) + y(t) \\P(t) = x_0ert + y_0ert\)
Taking the derivative with respect to t gives the rate of change of P(t) as follows:
\(dP/dt = x_0er + y_0er\)
This is a monotonically increasing function of t.
Therefore, the total population is smallest when the derivative is zero, that is, when er(\(x_0 + y_0\)) = 0.
This occurs when t = 0 or when \(x_0 + y_0 = 0.\)
for such more question on differential equations
https://brainly.com/question/28099315
#SPJ11
which expression is equivalent to 5^10 x 5^5
Answers
Answer:
\( {5}^{10 + 5} = {5}^{15} \)
Answer:
5^15
Step-by-step explanation:
when multiplying expressions with the same base you keep the base (the base is 5 ) and add the exponents (10 and 5) then you would get your awnser
find the lateral area of the prism!!
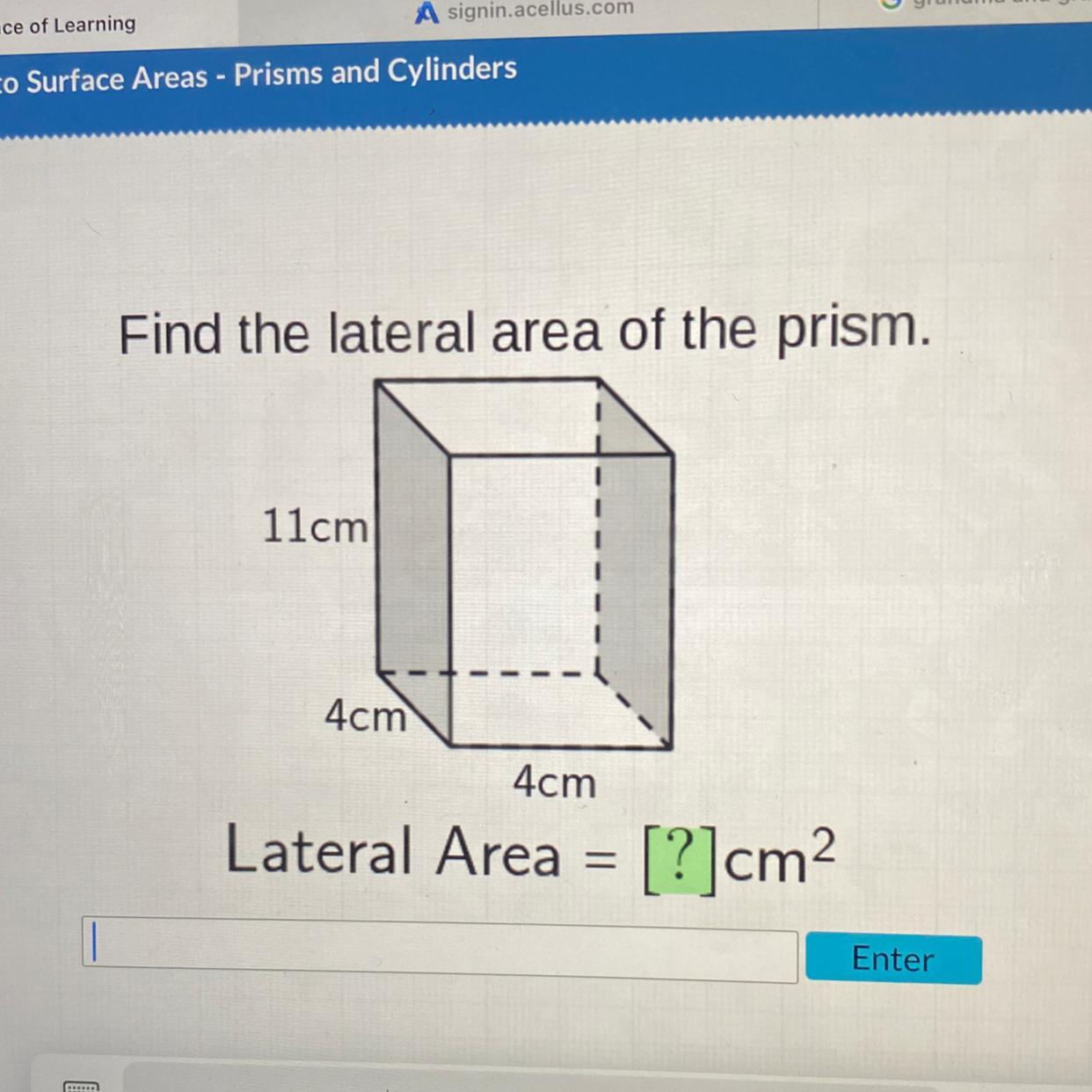
Answers
Check the picture below.
so we only want the area in pink.
\(\stackrel{\textit{left and right}}{2(4)(11)}~~ + ~~\stackrel{\textit{front and back}}{2(4)(11)}\implies \text{\LARGE 176}~cm^2\)

In the figure below, C is between A and D, and B is the midpoint of AC. If BC=3 and AD=13, find CD.
Answers
The length of CD is 7 units.
What is Distance?The length along a line or line segment between two points on the line or line segment.
Distance=√(x₂-x₁)²+(y₂-y₁)²
From the figure it is given that C is between A and D.
B is the midpoint of AC
BC=3 and AD=13, we have to find CD.
As B is the midpoint of AC, then BC=AB
BC=AB=3
AC=AB+BC=6
Now to find CD=AD-AC
CD=13-6
CD=7
Hence, the length of CD is 7 units.
To learn more on Distance click:
https://brainly.com/question/15172156
#SPJ1
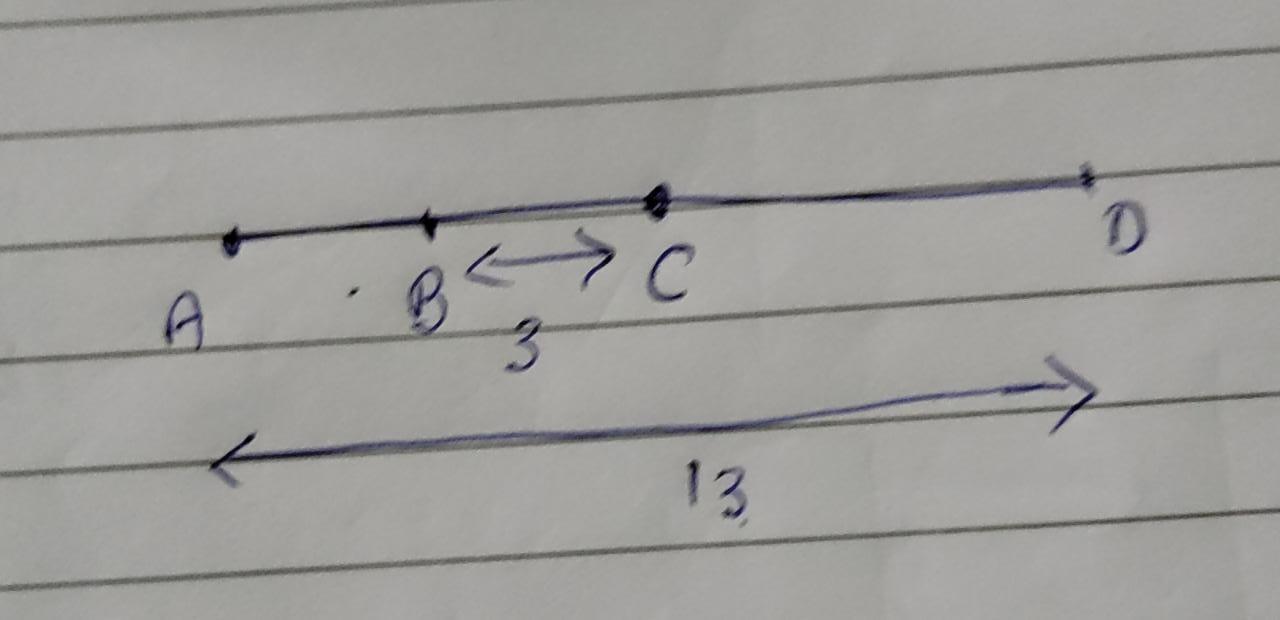
Help me with question 1

Answers
Answer:
The most logical answer would be C.
Step-by-step explanation:
What is the slope of a line perpendicular to the line below?
Responses
−3
negative 3
3
3
−13
negative 1 third
13
1 third
Skip to navigation

Answers
This means that if we were to draw a line perpendicular to the given line at any point, the slope of that line would be 3.
How is slope of a line determined?We must first determine the slope of the supplied line in order to determine the slope of a line perpendicular to the line passing through (-3, -1) and (0, -2).
We may determine the slope of the given line by using the slope formula (m = (y2 - y1) / (x2 - x1)) as follows:
m = (-2 - (-1)) / (0 - (-3)) = -1 / 3
The negative reciprocal of -1/3, or 3, would be the slope of a line that was perpendicular to this line.
As a result, a line perpendicular to the line passing between (-3, -1) and (0, -2) will have a slope of 3. This suggests that the slope of the line we would draw if we were to draw it perpendicular to the supplied line at any point would be 3.
Learn more about coordinate geometry here:
brainly.com/question/18269861
#SPJ1
how to subtract mixed fractions with whole numbers
Answers
The process to subtract the mixed fractions with the whole numbers is explained below.
The Mixed Fractions are defined as type of fraction that consists of a whole number and a proper fraction.
Step(i) : We multiply whole number by denominator of fraction and add numerator.
For example, if mixed fraction 2(1/3), we multiply 2 by 3 and add 1 to get 7. So, 2(1/3) is equivalent to improper fraction 7/3.
Step(ii) : Find a common denominator for fractions. We find least common multiple (LCM) of denominators.
For example, if you want to subtract 2(1/3) from 5, denominators are 3 and 1, and LCM is 3.
Step(iii) : Convert whole number to a fraction with same denominator as common denominator.
For example, if LCM is 3 and we want to subtract 2(1/3) from 5, we will convert 5 to fraction 15/3.
Step(iv) : Rewrite each fraction with common denominator.
For example, if we want to subtract 2(1/3) from 5, we rewrite 2(1/3) as 7/3 and 15/3 as 5.
Step(v) : Subtract the fractions.
For example, to subtract 7/3 from 5, we subtract numerators and keep the denominator: 15/3 - 7/3 = 8/3.
Learn more about Mixed Fractions here
https://brainly.com/question/29264210
#SPJ4
What is the binomial probability formula used for?
Answers
The binomial probability formula is used to calculate the probability of a specific number of successes in a fixed number of independent trials, where each trial can only result in success or failure. It is used to model situations where there are only two possible outcomes for each trial, and where the trials are independent and identically distributed.
The formula for binomial probability is:
\(P(x) = (n choose x) * p^x * (1 - p)^{n-x}\\\)
where P(x) is the probability of x successes in n trials, p is the probability of success on each trial, (n choose x) is the binomial coefficient which gives the number of ways to choose x successes from n trials, and (1 - p) is the probability of failure on each trial.
The binomial probability formula can be used in a variety of applications, such as:
Predicting the probability of a certain number of defective products in a production runEstimating the likelihood of a certain number of people out of a sample having a particular characteristicAnalyzing the probability of winning a certain number of games in a sports seasonFor more questions on Binomial Probability
https://brainly.com/question/9325204
#SPJ4
There are 4 green marbles and 7 silver marbles in a bag.You randomly choose one of the marbles .What is the probability of choosing a green marble?Please show step by step!
Answers
Answer:
4/11
Step-by-step explanation:
Notice that because there are 4 green marbles and 7 silver marbles, that there is a total of 11 marbles in the bag. The question is also looking at the number of green marbles and the probability of reaching into the bad and choosing a green marble. Here is a way to set the fraction up to get the right answer for these types of problems. green marbles/total
Plug in the data. The numerator is 4 and the denominator is 11. Therefore, you get 4/11
Answer:
Step-by-step explanation:
First, you will need to find out how many marbles there are total, which is 11. . Next, identify how many green marbles are in there, which is 4. You are able to identify that With you finding probability, the total amount will be on the bottom. So, you can see that there is a 4/11 or about 36% chance that a green marble will be picked.
Graph the function using six values of its domain, y=30 + 5x
Answers
Answer: Here ya go bro, answer is in picture below


Will mark branlist for the first one to help

Answers
Answer:
17°
Step-by-step explanation:
73°= EGB
EGB+ x° = 90°
so x° = 90°-73° =17°
Answer:
17°
73°= EGB
EGB+ x° = 90°
so x° = 90°-73° =17°
Step-by-step explanation:
Determine the truth value of each statement. The domain of discourse is R. Justify your answer. (a) Vr(x² +1>x) (b) Vx(x>1<})
Answers
For a statement to be true, it must be true in every possible case. The following are the truth values for each statement:
For all r in R, x²+1 > x is true.Vx (x > 1) is also true. Let's look at each statement's truth value. Vr(x²+1 > x) is the first one. Here, V is used as a universal quantifier. For any value of r in the domain of discourse R, the statement must be true. Since we're dealing with a quadratic function here, we can say that for any value of r, the function x²+1 is always greater than x, and the statement is therefore true. Now, let's look at Vx (x > 1). Here, we're using another universal quantifier, Vx. For every value of x in the domain of discourse R, the statement must be true. We know that any value of x that is greater than 1 will satisfy this inequality. As a result, the statement is true for every possible case. In conclusion, the truth values of both statements have been determined. For all r in R, x²+1 > x is true. Vx (x > 1) is also true.
To know more about truth values visit: brainly.com/question/29137731
#SPJ11
Given the endpoint x(11,-2) and the midpoint (4,3) find the missing endpoint y. Write answer as order pair.
Answers
9514 1404 393
Answer:
(-3, 8)
Step-by-step explanation:
For m the midpoint of xy, we have ...
m = (x+y)/2 ⇒ y = 2m-x
y = 2(4, 3) -(11, -2) = (2·4 -11, 2·3 +2)
y = (-3, 8)

can someone help me plz?


Answers
Answer:
1. 18g - 35
2. 16g - 25h
3. -4
Step-by-step explanation:
Find the measure of the indicated angle to the nearest degree.

Answers
1. use sin
inverse of sin(44/57) = 50.5 ---> 51°
2. use tan
inverse of tan(6/8) = 36.8 ---> 37°
3. use cos
inverse of cos(20/31) = 49.8 ---> 50°
4. use sin
inverse of sin(37/58) = 39.6 ---> 40°
The commission earned on the sale of a car can be represented by the equation c(p)=250+0.02p where c represents the commission and p represents the purchase price of a car.
Jack sold two cars last weekend, one for $15,075 and the other for $21,640. Find his total commission.
If c(p)=745.80, find the purchase of the car.
i've tried the answers someone else found on here but they don't work so plss help
Answers
Answer:
1) His total commission is $1,234.3
2) The purchase of the car is $24,790.
Step-by-step explanation:
1) 21640*0.02=432.8+250=682.8
15075 0.02301.5+ 250-551.5
682.8+ 551.5-1,234.3
2) 745.8-250-495.8/0.02= 24,790
Step-by-step explanation:
don't guess around, just calculate yourself.
first he sold a car for $15,075.
c(15075) = 250 + 0.02×15075 = $551.50
then he sold another car for $21,640.
c(21640) = 250 + 0.02×21640 = $682.80
his total commission was
$551.50 + $682.80 = $1,234.30
c(p) = 745.80
what was p ?
745.8 = 250 + 0.02p
495.8 = 0.02p
p = 495.8/0.02 = $24,790
If this policyholder causes a huge, serious accident with both bodily injuries and property damage, what is the highest amount their liability coverage will provide?
A. ) $544. 58
B. ) $300,000
C. ) $400,000
D. ) Unlimited amounts, depending on the number of people injured
Answers
C). The highest amount their liability coverage will provide is $400,000
This is because most standard liability policies will provide up to $300,000 for bodily injury and $100,000 for property damage, but the policyholder may be able to purchase additional coverage for higher limits if they need it. The exact amount of coverage will depend on the policy the policyholder purchased.
Liability insurance is a component of the general insurance system of risk financing that protects the purchaser from the risks of liabilities imposed by lawsuits and similar claims, as well as the insured if the purchaser is sued for claims covered by the insurance policy.
For more questions like Liability coverage click the link below:
https://brainly.com/question/27020987
#SPJ4
The number of miles M that a certain automobile can travel onone gallon of gasoline at a speed of v mi/hr is given by:
M=-(1/30)v^2 + (5/2)v , for v<0<70
a. Find the most economical speed for a trip.
b. Find the largest value of M.
Answers
a. The most economical speed for a trip is v = 35 mph. and b. The largest value of M is M = 87.5 miles.
a. To find the most economical speed for a trip, we need to maximize the value of M, which represents the number of miles the automobile can travel on one gallon of gasoline.
Given equation: M = -(1/30)v² + (5/2)v
Take the derivative of M with respect to v using the power rule for derivatives:
dM/dv = -(2/30)v + (5/2)
Set the derivative equal to 0 and solve for v to find the critical point:
-(2/30)v + (5/2) = 0
-(2/30)v = -(5/2)
v = (5/2) * (30/-2)
v = 35
Since v must be less than 70 according to the given range, the most economical speed for the trip is v = 35 mph.
b. To find the largest value of M, we can substitute the given expression for M into the equation and evaluate it for the given range of v, which is v < 0 < 70.
Given equation: M = -(1/30)v² + (5/2)v
Substitute v = 70 into the equation to find the largest value of M:
M = -(1/30)(70)² + (5/2)(70)
M = -4900/30 + 350/2
M = -163.33 + 175
M = 11.67
Therefore, the largest value of M is M = 87.5 miles. (rounded to two decimal places)
To know more about speed, refer here:
https://brainly.com/question/17661499#
#SPJ11
28% of how many peaches is 7 peaches.
Answers
The total number of peaches is given by the equation A = 25 peaches
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the total number of peaches be represented as A
Now , the equation will be
The percentage of peaches that equals 7 peaches = 28 %
Substituting the values in the equation , we get
28 % of A = 7 be equation (1)
On simplifying the equation , we get
( 28 / 100 ) x A = 7
Multiply by 100 on both sides of the equation , we get
28A = 700
Divide by 28 on both sides of the equation , we get
A = 700/28
A = 25 peaches
Therefore , the value of A is 25 peaches
Hence , the number of peaches is 25 peaches
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
A squirrel burrowed 4 holes in 6 minutes. How many holes
could the squirrel burrow in 9 minutes?
Answers
Answer:
The squirrel could burrow 6 holes in 9 minutes.
Step-by-step explanation: