City park is a square piece of land with an area of 10,000 square yards.Write and solve an equation to find the perimeter of the park.
Answers
The area of an square is given by:
\(A=l^2\)Where "A" is the area and "l" is the length of the side of the square. Using this we can find the length of the sides of the park.
\(\begin{gathered} 10000=l^2 \\ l=\sqrt{10000} \\ l=100 \end{gathered}\)The length of the sides is 100 yards. The perimeter of a square is given by:
\(P\text{ = 4}\cdot l\)Where P is the perimeter and l is the length of the sides, since we know the length of each side in this case we can calculate the perimeter.
\(P=4\cdot10000=40000\)The perimeter is 40,000 yards.
Related Questions
It costs 100 dollars to rent the bowling alley, plus 4 dollars per person the cost for any number (n) of people can be found using this expression 100+ 4n the cost for 15 people equals ____ whole number only pls help and explain
Answers
so the cost is $160
(a) From Latoya's results, compute the experimental probability of rolling a 1 or 6.
(b)Assuming that the cube is fair, compute the theoretical probability of rolling a 1 or 6.
(c)Assuming that the cube is fair, choose the statement below that is true.
A. The experimental and theoretical probabilities must always be equal.
B. As the number of rolls increases, we expect the experimental and theoretical probabilities to
become closer, though they might not be equal.
C. As the number of rolls increases, we expect the experimental and theoretical probabilities to
become farther apart.

Answers
(a) To compute the experimental probability of rolling a 1 or 6 from Latoya's results, we need to determine the number of times a 1 or 6 was rolled and divide it by the total number of rolls Latoya made.
Let's assume that Latoya rolled the dice 100 times and obtained 20 1's and 10 6's. The total number of successful outcomes (rolling a 1 or 6) is 20 + 10 = 30.
Therefore, the experimental probability of rolling a 1 or 6 is 30/100 = 0.3 or 30%.
(b) Assuming the cube is fair, the theoretical probability of rolling a 1 or 6 can be determined by considering the favorable outcomes (rolling a 1 or 6) divided by the total possible outcomes (rolling any number from 1 to 6).
Since there are two favorable outcomes (1 and 6) out of six possible outcomes (1, 2, 3, 4, 5, 6), the theoretical probability is 2/6 = 1/3 or approximately 0.3333.
(c) The correct statement is B. As the number of rolls increases, we expect the experimental and theoretical probabilities to become closer, though they might not be equal. This is due to the law of large numbers, which states that as more trials are conducted, the experimental probability tends to converge towards the theoretical probability. However, it is not necessary for them to be exactly equal. Random variations can cause some discrepancy, but with a larger number of rolls, the experimental probability should approach the theoretical probability more closely.
For such more question on probability
https://brainly.com/question/30390037
#SPJ8
Use the function below to find F(3).

Answers
Hello,
Answer: D
Step-by-step explanation:
F(x) = (1/5)ˣ
F(3) = (1/5)³ = 1³/5³ = 1/125
⇒ Answer D
Please help
what is the measure in degrees of the highlighted ( the middle one) angle

Answers
Answer:
8x+7x+44.4=180
15x=180-44.4
15x =135.6
X=9.04
8x=9.04×8=72.32
Will yall help me pleaseee! I need this turned in today donttake my points :'( this is Pythagorean Math !!!!

Answers
Answer:
1. 7.6 = c
2. 45 = c
Step-by-step explanation:
1. 3^2 + 7^2 = c^2
9 + 49 = c^2
58 = c^2
square root both sides = 7.6 = c
2. 27^2 + 36^2 = c^2
729 + 1296 = c^2
2025 = c^2
square root both sides
c = 45
PLEASE ANSWER FAST I HAVE 10 MINUTES LEFT AND ILL GIVE BRAINLIEST IF CORRECT!
Which graph shows the result of dilating this figure by a factor of 4 about the origin? On a coordinate plane, rectangle A B C D has points (negative 1, 1), (3, 1), (3, negative 1), (negative 1, negative 1). On a coordinate plane, rectangle A prime B prime C prime D prime has points (negative 4, 4), (12, 4), (12, negative 4), (negative 4, negative 4). On a coordinate plane, rectangle A prime B prime C prime D prime has points (negative 2, 2), (6, 2), (6, negative 2), (negative 2, negative 2). On a coordinate plane, rectangle A prime B prime C prime D prime has points (negative 0.25, 0.25), (0.75, 0.25), (0.75, negative 0.25). (negative 0.25, negative 0.25). On a coordinate plane, rectangle A prime B prime C prime D prime has points (negative 0.5, 0.5), (1.5, 0.5), (1.5, negative 0.5), (negative 0.5, negative 0.5).
Answers
Answer:
It would be the first choice, A'B'C'D' with points (-4, 4); (12, 4); (12, -4); and (-4, -4)
Step-by-step explanation:
Each point on rectangle A'B'C'D are 4 times the original distance from the origin as the rectangle ABCD.
Answer:
Ummm the first choice?
Step-by-step explanation:
I guessing and not reading
Using trial and improvement, find the solution between 3 and 4 for the following equation: 2 x 3 − x 2 = 100 Give your answer rounded to 1 DP.
Answers
The solution is, After decreasing £16870 by 3% we get, £16363.90.
Here, we have,
A percentage is a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign, "%".
First, find the percentage of £16870 by 3%
%value = 3% * 16870
= (3 / 100) * 16870
= 506.1
Now, just minus with actual value
New value = actual value - %value
We know, actual value = £16870 and %value = 506.1
so, New value = 16870 - 506.1
we get, New value = £16363.90
Therefore, After decreasing £16870 by 3% we get, £16363.90
To read more about Percentage.
brainly.com/question/25896797
#SPJ1
complete question:
Decrease £16870 by 3%
Give your answer rounded to 2 DP.
2. (7 points) If f(x) = -5 cosx+xtanx, find df and evaluate if x = pi/4 and dx = 1/24
Answers
The value of df, when x = π/4 and dx = 1/24, is (-5π - 5√2)/(96√2).
To find the derivative of the function f(x) = -5cos(x) + xtan(x), we'll use the sum and product rules of differentiation. Let's start by finding df/dx.
Apply the product rule:
Let u(x) = -5cos(x) and v(x) = xtan(x).
Then, the product rule states that (uv)' = u'v + uv'.
Derivative of u(x):
u'(x) = d/dx[-5cos(x)] = -5 * d/dx[cos(x)] = 5sin(x) [Using the chain rule]
Derivative of v(x):
v'(x) = d/dx[xtan(x)] = x * d/dx[tan(x)] + tan(x) * d/dx[x] [Using the product rule]
= x * sec^2(x) + tan(x) [Using the derivative of tan(x) = sec^2(x)]
Applying the product rule:
(uv)' = (5sin(x))(xtan(x)) + (-5cos(x))(x * sec^2(x) + tan(x))
= 5xsin(x)tan(x) - 5xcos(x)sec^2(x) - 5cos(x)tan(x)
Simplify the expression:
df/dx = 5xsin(x)tan(x) - 5xcos(x)sec^2(x) - 5cos(x)tan(x)
Now, we need to evaluate df/dx at x = π/4 and dx = 1/24.
Substitute x = π/4 into the derivative expression:
df/dx = 5(π/4)sin(π/4)tan(π/4) - 5(π/4)cos(π/4)sec^2(π/4) - 5cos(π/4)tan(π/4)
Simplify the trigonometric values:
sin(π/4) = cos(π/4) = 1/√2
tan(π/4) = 1
sec(π/4) = √2
Substituting these values:
df/dx = 5(π/4)(1/√2)(1)(1) - 5(π/4)(1/√2)(√2)^2 - 5(1/√2)(1)
Simplifying further:
df/dx = 5(π/4)(1/√2) - 5(π/4)(1/√2)(2) - 5(1/√2)
= (5π/4√2) - (10π/4√2) - (5/√2)
= (5π - 10π - 5√2)/(4√2)
= (-5π - 5√2)/(4√2)
= (-5π - 5√2)/(4√2)
Now, to evaluate df/dx when dx = 1/24, we'll multiply the derivative by the given value:
df = (-5π - 5√2)/(4√2) * (1/24)
= (-5π - 5√2)/(96√2)
for such more question on derivative
https://brainly.com/question/23819325
#SPJ8
Find the missing angle and side measures of Delta*ABC , given that
m angle A = 50 deg , m angle C = 90 deg , and CB = 16
Answers
The missing angle is <B= 40 degree and missing side length is AB = 12.25 and AC = 19.068.
To find the missing angle and side measures of ΔABC, we can use the properties of a triangle.
Given:
∠A = 50°
∠C = 90°
CB = 16
We can start by finding the measure of ∠B:
∠A + ∠B + ∠C = 180° (Sum of angles in a triangle)
50° + ∠B + 90° = 180°
∠B + 140° = 180°
∠B = 180° - 140°
∠B = 40°
Now, using Sine law
CB/ sin A = AB / sin C
16 / sin 50 = AB / sin 90
16 / 0.766044 = AB
AB = 12.25
Again 12.25 = AC/ sin B
12.25 = AC / sin 40
AC = 19.068
Learn more about sine law here:
https://brainly.com/question/13098194
#SPJ1
2x + 2 = 5x -8 simplify
Answers
Answer, x = 1
Using a breakeven analysis, determine how long it would take for the following options in auto insurance deductibles / premiums to break even.
Option 1: $500 deductible comes with a $775 annual premium.
Option 2: $1,000 deductible comes with a $650 annual premium.
How many years without a claim would it take for the two options to break even?
Answers
Answer: It would take 4 years without a claim for Option 2 to break even with Option 1. After 4 years, the savings from the lower premium on Option 2 would offset the higher deductible, resulting in lower total cost.
Step-by-step explanation: To calculate the break-even point, we need to determine the point at which the savings from the lower premium on Option 2 offset the higher deductible.
Option 1:
Annual Premium = $775
Deductible = $500
Option 2:
Annual Premium = $650
Deductible = $1000
Let x be the number of years without a claim.
For Option 1, the total cost over x years would be:
Total Cost = $775x + $500
For Option 2, the total cost over x years would be:
Total Cost = $650x + $1000
To find when the two options break even, we need to set these two equations equal to each other and solve for x:
775x + 500 = 650x + 1000
125x = 500
x = 4
Therefore, it would take 4 years without a claim for Option 2 to break even with Option 1. After 4 years, the savings from the lower premium on Option 2 would offset the higher deductible, resulting in lower total cost.
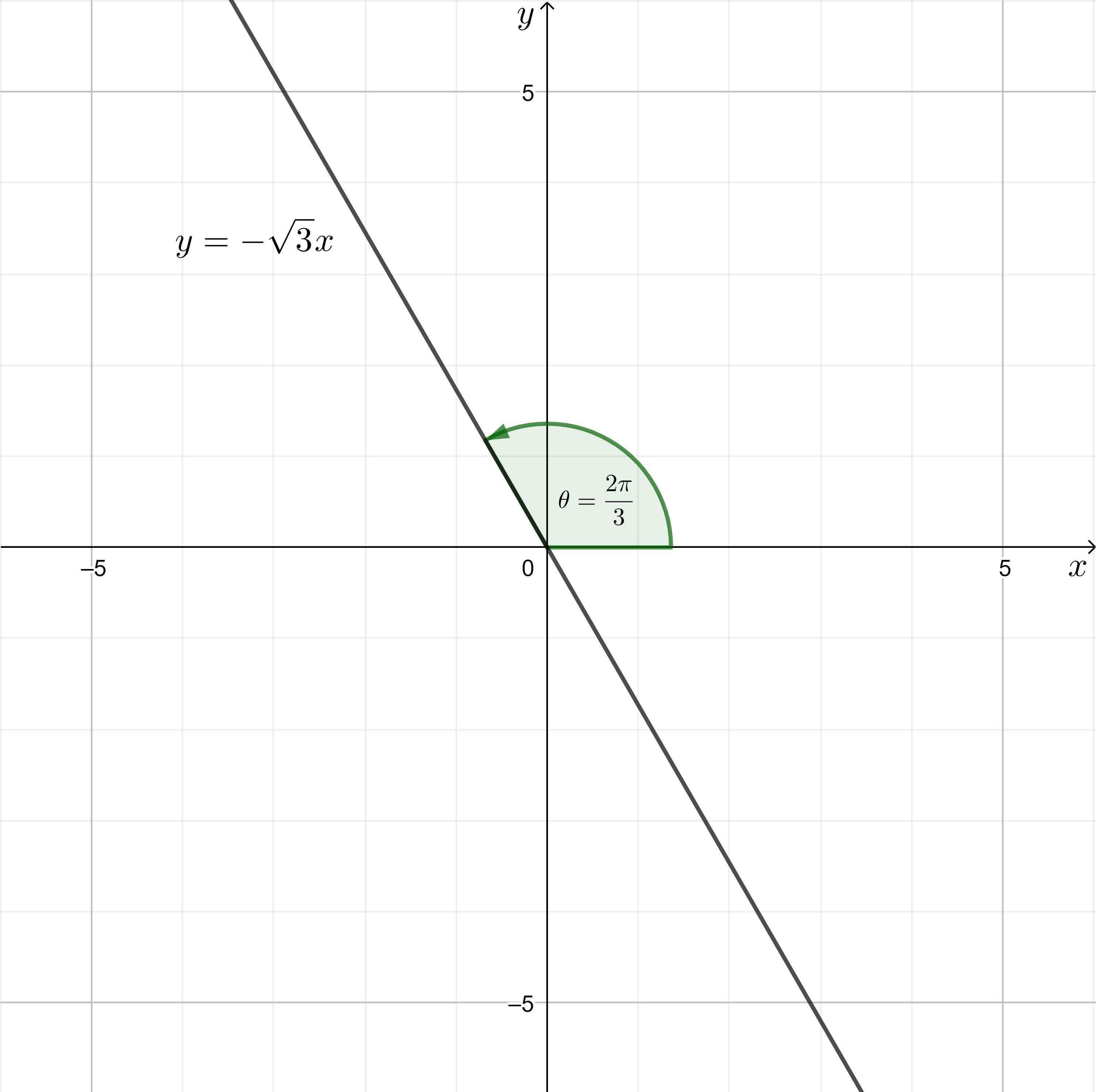
Which equation is the polar equivalent to the equation y = - sqrt(3) x?

Answers
θ = 5π/6 is the polar equivalent to the equation y= -√3x.
To determine the polar equivalent of the equation y = -√3x, we need to convert it from rectangular coordinates (x, y) to polar coordinates (r, θ).
In polar coordinates, r represents the distance from the origin to the point, and θ represents the angle from the positive x-axis to the point.
To convert the equation, we need to substitute x and y in terms of r and θ. We can rewrite the given equation as:
r sin(θ) = -√3 r cos(θ)
Simplifying, we can divide both sides by r:
sin(θ) = -√3 cos(θ)
Using trigonometric identities, we can rewrite this equation as:
tan(θ) = -√3
Now, we need to find the value of θ that satisfies this equation.
The value of θ that satisfies tan(θ) = -√3 is θ = 5π/6 or 150 degrees.
Therefore, the polar equivalent of the equation y = -√3x is:
θ = 5π/6 (or 150 degrees)
For more such questions on polar equivalent
https://brainly.com/question/27971762
#SPJ8
Answer:
\(\theta =\dfrac{2\pi }{3}\)
Step-by-step explanation:
The polar equivalent refers to the representation of a mathematical equation, point, or shape in polar coordinates (r, θ) instead of Cartesian coordinates (x, y).
In Cartesian coordinates, the relationship between a point (x, y) and its polar coordinates (r, θ) can be described by the following equations:
\(\boxed{\begin{aligned}x &= r \cos \theta\\y &= r \sin \theta\end{aligned}}\)
where:
r represents the distance of the point from the origin (0, 0).θ represents the angle formed by the line connecting the point and the positive x-axis in polar coordinates.By substituting these expressions into the equation \(y = -\sqrt{3}x\), we get:
\(r \sin \theta=-\sqrt{3} \:r\cos \theta\)
Divide both sides of the equation by r:
\(\dfrac{r \sin \theta}{r}=\dfrac{-\sqrt{3} \:r\cos \theta}{r}\)
\(\sin \theta=-\sqrt{3} \cos \theta\)
Divide both sides of the equation by cos θ, and apply the trigonometric identity tan θ = sin θ / cos θ:
\(\dfrac{\sin \theta}{\cos \theta}=\dfrac{-\sqrt{3} \cos \theta}{\cos \theta}\)
\(\tan \theta =-\sqrt{3}\)
Solve for θ:
\(\theta =\tan^{-1}\left(-\sqrt{3}\right)\)
\(\theta =\dfrac{2\pi }{3}+\pi n\)
Therefore, the polar equivalent to the equation \(y = -\sqrt{3}x\) is:
\(\boxed{\theta =\dfrac{2\pi }{3}}\)
Solve the right triangle.
a = 3.3 cm, b = 1.7 cm, C = 90°
Round values to one decimal place.
Answers
Answer:
A = 62.7°B = 27.3°c = 3.7Step-by-step explanation:
tan(A) = a/b = 3.3/1.7
A = arctan(33/17) ≈ 62.7°
B = 90° -A = 27.3°
c = √(a²+b²) = √(3.3² +1.7²) = √13.78
c ≈ 3.7
3.1 Which basic property of operations was used in each of the following
calculations?
3.1.1 25 x 4 = 4 x 25 = 100
3.1.2 412 412 412 + (-412) = 0
3.1.3 25 +37
-
=
= 20 + 5+ 30+7
= 20 +30 +5+7
= 50+ 12 = 62
Answers
3.1.1 The basic property of operations used is the commutative property of multiplication.
3.1.2 The basic property of operations used is the additive inverse property.
3.1.3 The basic property of operations used is the associative property of addition.
3.1.1 The basic property of operations used in this calculation is the commutative property of multiplication. It states that the order of the factors in a multiplication problem can be rearranged without changing the product. In this case, the numbers 25 and 4 were swapped, resulting in the same product of 100.
3.1.2 The basic property of operations used in this calculation is the additive inverse property. It states that for any number, there exists an additive inverse such that when the number and its additive inverse are added together, the result is zero. In this case, adding 412 and its additive inverse (-412) results in zero.
3.1.3 The basic property of operations used in this calculation is the associative property of addition. It states that the grouping of numbers being added does not affect the sum. In this case, the numbers 25, 37, 20, 5, 30, and 7 were regrouped to facilitate easier mental addition. By grouping 25 and 37, and then grouping 20, 5, 30, and 7, the final sum of 62 is obtained, which is the same as adding all the numbers together in the original order.
for such more question on commutative property
https://brainly.com/question/2475734
#SPJ8
Find the common ratio of the geometric sequence –5,–30, -180,...

Answers
Answer:
6
Step-by-step explanation:
You have to find what to multiply by to get to the next term
-30 ÷ -5 = 6
- 180 ÷ -30 = 6
therfore the common ratio is 6
24. There are 45 houses in Grey's Lake subdivision. Each house uses 400 gallons of water each day. Write a division equation to represent the total number of gallons of water used daily in Grey's Lake subdivision.
Answers
Answer: 18000/45= gallons used daily
Step-by-step explanation:
400x45=18000
Answer: 18000/45 gallons used daily
Step-by-step explanation: 400x45=18000 gallons
A wiring job requires 4 electricians to work for 6 hours to finish the job.
On the day of the job, one electrician does not report. How long would it
take to complete the same job by the remaining electricians?

Answers
if we are talking about 24hrs. 24/4=6 so 24/3=8 (3 bc there is one less)!
The time and electricians it would take the remaining 3 electricians 8 hours to complete the job if one electrician does not report.
How are number of people to time needed to complete a task related?More people to do a task means less time it will take.
Less people to do a task means more time it will take.
Thus, they are inversely related.
If x men take y time for a work,
We can define a constant as "Manpower" needed for doing that specific work.
Let we define:
Manpower needed for a work = y + y + y + .. + y = Time per man × count of men
Manpower needed for a work = xy
We are given that;
Number of electricians= 4
Number of hours= 6
Now,
We can use the formula:
workers × time = work
where "workers" is the number of electricians, "time" is the number of hours they work, and "work" is the amount of work done.
In this case, we know that 4 electricians can complete the job in 6 hours. So:
4 × 6 = work
work = 24
This means that the total amount of work required to complete the job is 24 "units".
Now, if one electrician doesn't show up, we have only 3 electricians to do the work. Let's call the time it takes for the 3 electricians to complete the job "t".
So we have:
3 × t = 24
Dividing both sides by 3, we get:
t = 8
Therefore, by work and time answer will be 3 electricians and 8 hours.
Learn more about work and time here:
https://brainly.com/question/1063042
#SPJ2
Four roommates want to split the price of a computer. How much will each roommate pay? Write an equation and solve it by using the information in the table.
A 2-column table with 4 rows. Column 1 is labeled Electronics with entries Mp3 player, computer, tablet, smart phone. Column 2 is labeled Sale Price in dollars with entries 39, 299, 199, 78.
$49.75
$74.75
$156
$1196
Mark this and return Four roommates want to split the price of a computer. How much will each roommate pay? Write an equation and solve it by using the information in the table.
A 2-column table with 4 rows. Column 1 is labeled Electronics with entries Mp3 player, computer, tablet, smart phone. Column 2 is labeled Sale Price in dollars with entries 39, 299, 199, 78.
$49.75
$74.75
$156
$1196
Mark this and return Four roommates want to split the price of a computer. How much will each roommate pay? Write an equation and solve it by using the information in the table.
A 2-column table with 4 rows. Column 1 is labeled Electronics with entries Mp3 player, computer, tablet, smart phone. Column 2 is labeled Sale Price in dollars with entries 39, 299, 199, 78.
$49.75
$74.75
$156
$1196
Mark this and return Four roommates want to split the price of a computer. How much will each roommate pay? Write an equation and solve it by using the information in the table.
A 2-column table with 4 rows. Column 1 is labeled Electronics with entries Mp3 player, computer, tablet, smart phone. Column 2 is labeled Sale Price in dollars with entries 39, 299, 199, 78.
Four roommates want to split the price of a computer. How much will each roommate pay? Write an equation and solve it by using the information in the table.
A 2-column table with 4 rows. Column 1 is labeled Electronics with entries Mp3 player, computer, tablet, smart phone. Column 2 is labeled Sale Price in dollars with entries 39, 299, 199, 78.
$49.75
$74.75
$156
$1196
Mark this and return
$49.75
$74.75
$156
$1196
Mark this and return
$49.75
$74.75
$156
$1196
Mark this and return
Answers
Answer: $74.75
Step-by-step explanation:
Answer:
74.75 dolors i take test
Step-by-step explanation:

a number cube is tossed 60 times Determine the experimental probability of landing on a number less than two
Answers
Answer:
1.67% approx
Step-by-step explanation:
To determine the experimental probability of landing on a number less than two when a number cube is tossed 60 times, we need to count the number of times the number on the cube is less than two and divide it by the total number of tosses.
Let's denote the event of landing on a number less than two as "A." We'll count the number of successful outcomes, where the number on the cube is less than two.
Assuming the number cube is fair and unbiased, it has six sides numbered from 1 to 6. Out of these, only one side has a number less than two, which is one.
Now, we can calculate the experimental probability using the formula:
Experimental Probability (P(A)) = Number of successful outcomes / Total number of tosses
In this case, the number of successful outcomes is the number of times the cube lands on a number less than two, which is one. The total number of tosses is given as 60.
Therefore, the experimental probability of landing on a number less than two is:
P(A) = 1 (successful outcomes) / 60 (total number of tosses)
= 1/60
≈ 0.0167 or 1.67%
So, the experimental probability of landing on a number less than two is approximately 0.0167 or 1.67%.
obove answer is correct i think
Please Help Me Do This I cant understand it no matter how hard I try. (Problem in the image)

Answers
Answer:
7.3
Step-by-step explanation:
The length of AB is found using the distance formula
We need to know the coordinates of A and B
A = (-5,-4) and B = (-3,3)
The distance is
d = sqrt ( (y2-y1)^2 + (x2-x1)^2)
= sqrt( (3 - -4)^2 +(-3 - -5)^2)
= sqrt( (3+4)^2 +(-3+5)^2)
= sqrt(7^2+2^2)
= sqrt(49+4)
= sqrt(53)
=7.280109889
To the nearest hundredth
=7.3
I neeed help asapppppp (I’ll put you as brainlest if you help) (15 points)

Answers
Answer:
7$4.45.......?!!!!!!!!!
In the triangle below, b =________. If necessary, round your answer to two
decimal places.
A
42°
C
Answer here
B
41.5%
37

Answers
Answer:
b ≈ 54.94
Step-by-step explanation:
using the Sine rule in Δ ABC
\(\frac{a}{sinA}\) = \(\frac{b}{sinB}\) = \(\frac{c}{sinC}\)
where a is the side opposite ∠ A, b is opposite ∠ B , c is opposite ∠ C
we require to calculate ∠ B
∠ B = 180° - (42 + 41.5)° = 180° - 83.5° = 96.5°
to find b using the pair of ratios
\(\frac{b}{sinB}\) = \(\frac{a}{sinA}\) ( substitute values )
\(\frac{b}{sin96.5}\) = \(\frac{37}{sin42}\) ( cross- multiply )
b × sin42° = 37 × sin96.5° ( divide both sides by sin42° )
b = \(\frac{37sin96.5}{sin42}\) ≈ 54.94 ( to 2 decimal places )
2. The diagram above shows a wooden structure in the form of a cone mounted on hemispherical base. The vertical height of the cone is 24cm and the base 7cm. Calculate correct to 3 significant figures the surface area of the structure. (Take π= 22/7)
Answers
The surface area of the wooden structure is approximately 1012 cm².
To calculate the surface area of the wooden structure, we need to find the surface area of the cone and the surface area of the hemispherical base, and then add them together.
Surface Area of the Cone:
The surface area of a cone is given by the formula:
A_{cone = \(\pi \times r_{cone} \times (r_{cone} + s_{cone})\), \(r_{cone\) is the radius of the base of the cone and \(s_{cone\) is the slant height of the cone.
The vertical height of the cone is 24 cm, and the base radius is 7 cm, we can calculate the slant height using the Pythagorean theorem:
\(s_{cone\) = \(\sqrt{(r_{cone}^2 + h_{cone}^2).\)
Using the given measurements:
\(s_{cone\) = √(7² + 24²) cm
\(s_{cone\) ≈ √(49 + 576) cm
\(s_{cone\) ≈ √625 cm
\(s_{cone\) ≈ 25 cm
Now, we can calculate the surface area of the cone:
\(A_{cone\) = π × 7 cm × (7 cm + 25 cm)
\(A_{cone\) = (22/7) × 7 cm × 32 cm
\(A_{cone\) = 704 cm²
Surface Area of the Hemispherical Base:
The surface area of a hemisphere is given by the formula:
\(A_{hemisphere\) = \(2 \times \pi \times r_{base}^2\), \(r_{base\) is the radius of the base of the hemisphere.
Given that the base radius is 7 cm, we can calculate the surface area of the hemispherical base:
\(A_{hemisphere\) = 2 × (22/7) × (7 cm)²
\(A_{hemisphere\) = (22/7) × 2 × 49 cm²
\(A_{hemisphere\) = 308 cm²
Total Surface Area:
To calculate the total surface area, we add the surface area of the cone and the surface area of the hemispherical base:
Total Surface Area = \(A_{cone} + A_{hemisphere}\)
Total Surface Area = 704 cm² + 308 cm²
Total Surface Area = 1012 cm²
For similar questions on surface area
https://brainly.com/question/16519513
#SPJ8
The equation of a parabola is (x−3)2=16(y+7) . What are the coordinates of the vertex and focus of the parabola? What is the equation of the directrix?
Answers
The coordinates of the vertex of the parabola are (3, -7). The focus of the parabola is located at (3, -3). The equation of the directrix is y = -11.
The given equation of the parabola is in the form (x - h)^2 = 4p(y - k), where (h, k) represents the vertex and p represents the distance between the vertex and the focus/directrix.
Comparing the given equation with the standard form, we can see that the vertex is at (3, -7).
The coefficient 4p in this case is 16, so p = 4. Since the parabola opens upward, the focus will be p units above the vertex. Therefore, the focus is located at (3, -7 + 4) = (3, -3).
To find the directrix, we need to consider the distance p below the vertex. Since the parabola opens upward, the directrix will be p units below the vertex. Hence, the equation of the directrix is y = -7 - 4 = -11.
In summary, the coordinates of the vertex are (3, -7), the focus is located at (3, -3), and the equation of the directrix is y = -11.
for such more questions on parabola
https://brainly.com/question/29635857
#SPJ8
In a class, 60%, of students are on a sports team and 20%, of students are in the orchestra. If 70%, of students in the class are on a sports team or in the orchestra, what is the probability a student randomly selected from the class is in the orchestra and on a sports team?
Answers
Answer: 10%
I had this same question earlier, 10% is the right answer
Can someone help me with this pleasee here is the picture

Answers
The system of equations as an augmented matrix is \(\left[\begin{array}{ccc|c}1&0&0&100\\0&-5&-7&350\\0&-5&-9&200\end{array}\right]\)
Writing the system of equations as an augmented matrixFrom the question, we have the following parameters that can be used in our computation:
x = 100
-5m - 7c = 350
-5m - 9c = 200
The above means that the variables in the system of equations are
x, m and c
So, we have the following representation
x m c
1 0 0 100
0 -5 -7 350
0 -5 -9 200
When represented as an augmented matrix, we have
\(\left[\begin{array}{ccc|c}1&0&0&100\\0&-5&-7&350\\0&-5&-9&200\end{array}\right]\)
Hence, the augmented matrix is \(\left[\begin{array}{ccc|c}1&0&0&100\\0&-5&-7&350\\0&-5&-9&200\end{array}\right]\)
Read more about matrix at
https://brainly.com/question/11989522
#SPJ1
Select the correct answer.
If no denominator equals zero, which expression is equivalent to 15/x-6 + 7/x+6?
A.
OB.
OC.
OD.
22 +132
²36
22-48
236
22
C.36
22 +48
²36

Answers
The expression in the options which is equivalent to the given expression is D. (22x + 48) / (x² - 36).
Given expression is,
[15 / (x - 6)] + [7 / (x + 6)]
Cross multiplying the two fractional expressions,
= [15 (x + 6) + 7 (x - 6)] / [(x - 6) (x + 6)]
= [15x + 90 + 7x - 42] / [x² - 6²]
= (22x + 48) / (x² - 36)
Hence the equivalent expression is D.
Learn more about Expressions here :
https://brainly.com/question/28170201
#SPJ1
Which is true about the solution to the system of inequalities shown? y > 3x + 1 y < 3x – 3 On a coordinate plane, 2 solid straight lines are shown. The first line has a positive slope and goes through (negative 2, negative 5) and (0, 1). Everything to the left of the line is shaded. The second line has a positive slope and goes through (0, negative 3) and (1, 0). Everything to the right of the line is shaded. Only values that satisfy y > 3x + 1 are solutions. Only values that satisfy y < 3x – 3 are solutions. Values that satisfy either y > 3x + 1 or y < 3x – 3 are solutions. There are no solutions.
Answers
There are no solutions to the system of inequalities Option (d)
Inequalities are a fundamental concept in mathematics and are commonly used in solving problems that involve ranges of values.
A system of two inequalities is a set of two inequalities that are considered together. In this case, the system of inequalities is
y > 3x + 1
y < 3x - 3
The inequality y > 3x + 1 represents a line on the coordinate plane with a slope of 3 and a y-intercept of 1. The inequality y < 3x - 3 represents another line on the coordinate plane with a slope of 3 and a y-intercept of -3. We can draw these lines on the coordinate plane and shade the regions that satisfy each inequality.
The first line has a positive slope and goes through (negative 2, negative 5) and (0, 1). Everything to the left of the line is shaded. The second line has a positive slope and goes through (0, negative 3) and (1, 0). Everything to the right of the line is shaded.
We can start by analyzing the inequality y > 3x + 1. This inequality represents the region above the line with a slope of 3 and a y-intercept of 1. Therefore, any point that is above this line satisfies this inequality.
Next, we analyze the inequality y < 3x - 3. This inequality represents the region below the line with a slope of 3 and a y-intercept of -3. Therefore, any point that is below this line satisfies this inequality.
To determine which values satisfy both inequalities, we need to find the region that satisfies both inequalities. This region is the intersection of the regions that satisfy each inequality.
When we analyze the regions that satisfy each inequality, we see that there is no region that satisfies both inequalities. Therefore, there are no values that satisfy the system of inequalities shown.
There are no solutions to the system of inequalities y > 3x + 1 and y < 3x - 3 by analyzing the regions that satisfy each inequality on a coordinate plane. The lack of a solution is determined by the fact that there is no region that satisfies both inequalities.
To know more about Inequalities here
https://brainly.com/question/28823603
#SPJ1
Complete Question :
Which is true about the solution to the system of inequalities shown?
y > 3x + 1
y < 3x – 3
On a coordinate plane, 2 solid straight lines are shown. The first line has a positive slope and goes through (negative 2, negative 5) and (0, 1). Everything to the left of the line is shaded. The second line has a positive slope and goes through (0, negative 3) and (1, 0). Everything to the right of the line is shaded.
Options:
a)Only values that satisfy y > 3x + 1 are solutions.
b)Only values that satisfy y < 3x – 3 are solutions.
c)Values that satisfy either y > 3x + 1 or y < 3x – 3 are solutions.
d)There are no solutions.
Answer:
D
Step-by-step explanation:
There are 54 girls on the playground. There are 25 fewer boys than girls on the playground. How many kids are on the playground?
Answers
Answer:
83 kids total
Step-by-step explanation:
There are 54 girls on the playground. There are 25 fewer boys than girls on the playground. How many kids are on the playground?
girls = 54
boys = 54 - 25 = 29
54 + 29 = 83 kids total
kids that are on the playground are 83.
What is the sum?Merging objects and identifying them since one big bunch is done through addition. In arithmetic, addition is the technique of adding two or more integers together. The product can meet are the quantities that are included, and the outcome of the operation, or the final response, is referred to as the sum.
The total number of girls that are present is 54
The data given is that there are
25 fewer boys taht are4 present
The total number of boys will be
boys = 54 - 25 = 29
The number of kids that are present will be the total of boys and girls that are present.
Kids = boys + girls
54 + 29 = 83 kids total
The quantity of kids that are present in the playground is 83.
Learn more about sum, here:
https://brainly.com/question/537797
#SPJ2
Solve for r to two decimal places.
8=e^4r
r = ______.
(Do not round until the final answer. Then round to the nearest hundredth as needed.)
Answers
Answer:
r = 0.52 to the nearest hundredth
Step-by-step explanation:
Here, given that ;
e^4r = 8
We want to find the value of r
To do this, we will need to find the ln of both sides
Mathematically;
ln(e^4r) = ln 8
4r ln e = ln 8
Mathematically; ln e = 1
Thus;
4r = ln 8
4r = 2.07944154168
r = 2.07944154168/4
r = 0.51986038542
To the nearest hundredth, r = 0.52