Consider the table of restaurants in the country.Restaurant QuantitySubway25,549McDonald's14,146KFC22,621Pizza Hut18,431Total Stores80,747A. Calculate the ratio of Subway restaurants to McDonald's restaurants as a decimal to the thousandths place andwrite a meaningful sentence. Is this part-to-part or part-to-whole?B. Calculate the KFC restaurants to the total restaurants ratio as a decimal to the thousandths place and write ameaningful sentence. Is this part-to-part or part-to-whole?

Answers
A. To compute the ratio of Subway restaurants to McDonald's restaurants, we divide the number of Subway restaurants (25,549) by the number of McDonald's restaurants (14,146) :
\(\begin{gathered} r=\frac{\#\text{Subway}}{\#McDonald^{\prime}s} \\ r=\frac{25,549}{14,146} \\ r=1.806 \end{gathered}\)• The ratio of Subway restaurants to McDonald's restaurants to the thousandths place is 1.806.
,• This is a part-to-part ratio because this ratio is relating the number of two franchises of restaurants.
B. To compute the ratio of KFC restaurants to the total of restaurants, we divide the number of KFC restaurants (22,621) by the total number of restaurants (80,747):
\(\begin{gathered} r=\frac{\#\text{KFC}}{\#\text{Total}} \\ r=\frac{22,621}{80,747} \\ r=0.280 \end{gathered}\)• The ratio of KFC restaurants to the thousandths place is 0.280.
,• This is a part-to-whole ratio because this ratio is relating the number of restaurants of a franchise to the total number of restaurants.
Related Questions
Need help with math homework
e^x=10^(x-1)
Answers
Answer:
Step-by-step explanation:
This equation represents the relationship between the exponential functions y = e^x and y = (10^(x-1)). These two functions are equal to each other for all values of x. This can be shown by taking the natural logarithm of both sides of the equation, which gives us:
ln(e^x) = x-1
In this equation, ln(e^x) is equal to x, since the natural logarithm of an exponential expression with a base of e is the exponent. Therefore, we can simplify the equation by taking the natural logarithm of both sides:
ln(10^(x-1)) = x-1
e^(x-1) = 10^x
The two functions e^x and 10^(x-1) are the same function with different bases, so they follow the same pattern. The fact that these two functions are equal to each other for all values of x can also be shown by graphing the two functions and seeing that they overlap perfectly.
find the area of a rectangle that measures 3 feet by 4 inches. Give area in square inches
Answers
Answer:
3×4
Step-by-step explanation:
12 +12=24 so that how you do it bye
Rewrite the following expression using the Distributive Property. 5(2x -8)
A. -30x
B. 10x -40
C. 10x + 40
D. 10x -8
I think it is either B or C but I'm not sure.
Answers
Answer:
B. 10x -40
Step-by-step explanation:
To rewrite the expression 5(2x-8) using the distributive property, we need to separate the expression inside the parentheses and then multiply the two expressions by 5. The answer is: 10x-40.
Help with this trig identities problems.
1) Given csc Φ = 7/3 and cot Φ = - (2√10)/(3), find sec Φ.
2) Given that sec β = 6/5 and sin β > 0, find tan β and sin β.
Answers
Using trigonometric identities, we found that sec Φ = -7/(2√10), sin Φ = 3/7, tan β = √11/5, and sin β = √11/6 for the given values of csc Φ, cot Φ, and sec β.
1. We can start by using the Pythagorean identity to find the values of sin Φ:
\(sin^2\) Φ + \(cos^2\) Φ = 1
Since csc Φ = 1/sin Φ, we can substitute and solve for sin Φ:
1/(7/3) = sin Φ
sin Φ = 3/7
Next, we can use the fact that cot Φ = cos Φ/sin Φ:
cot Φ = cos Φ/(3/7) = - (2√10)/(3)
Simplifying this expression, we get:
cos Φ = - (2√10)/(3) * (3/7) = - 2√10/7
Finally, we can use the fact that sec Φ = 1/cos Φ:
sec Φ = 1/(- 2√10/7) = -7/(2√10)
2. We can use the fact that sec β = 1/cos β to find the value of cos β:
sec β = 6/5
cos β = 5/6
Next, we can use the Pythagorean identity to find the value of sin β:
\(sin^2\) β + \(cos^2\) β = 1
sin β = √(1 - \(cos^2\) β) = √(1 - 25/36) = √(11/36) = √11/6
Finally, we can use the fact that tan β = sin β/cos β:
tan β = (√11/6)/(5/6) = √11/5
To learn more about Pythagorean please click on below link
https://brainly.com/question/29069676
#SPJ1
Please help and show how you found the answer step by step.
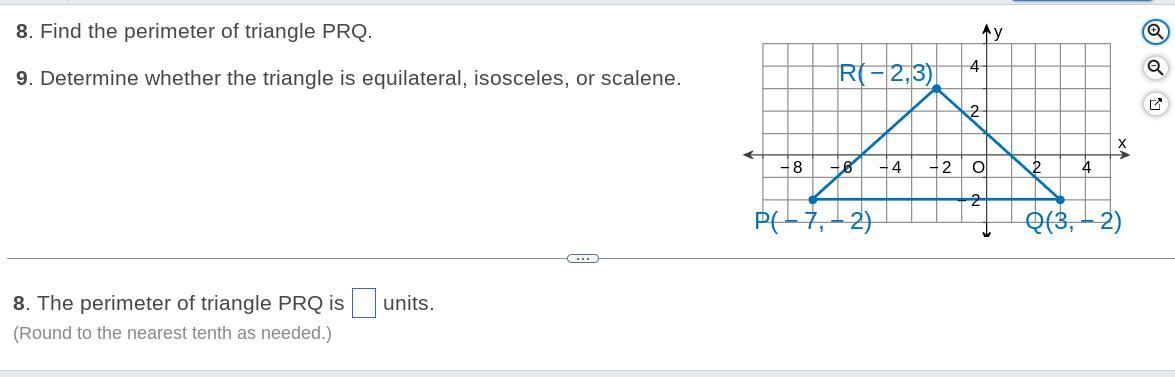
Answers
According to the information, the perimeter of the triangle is ≈ 31.18
How to calculate the perimeter of the triangle?To find the distance between two points, we can use the distance formula:
distance = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Let's label the coordinates as follows:
Point 1: (-2, 3)
Point 2: (3, -2)
Now we can substitute these values into the distance formula:
distance = sqrt((3 - (-2))^2 + (-2 - 3)^2)
distance = sqrt((5)^2 + (-5)^2)
distance = sqrt(25 + 25)
distance = sqrt(50)
distance ≈ 7.07
Therefore, the distance from (-2, 3) to (3, -2) is approximately 7.07 units.
To find the perimeter of the triangle, we need to find the length of all three sides of the triangle and then add them up.
Using the distance formula, we can find the length of the sides:
Side 1: (-2,3) to (3,-2)
d = √[(3 - (-2))^2 + (-2 - 3)^2]
= √[5^2 + (-5)^2]
= √50
= 5√2
Side 2: (3,-2) to (-7,-2)
d = √[(-7 - 3)^2 + (-2 - (-2))^2]
= √[(-10)^2 + 0^2]
= 10
Side 3: (-7,-2) to (-2,3)
d = √[(-2 - (-7))^2 + (3 - (-2))^2]
= √[5^2 + 5^2]
= 5√2
Therefore, the perimeter of the triangle is:
5√2 + 10 + 5√2 = 15√2 + 10 ≈ 31.18 (rounded to two decimal places)
An two of the three sides are equal, so it is an isosceles triangle.
Lean more about isosceles triangle in: https://brainly.com/question/2456591
#SPJ1
How do you find the surface area of the pyramid

Answers
The pyramid's surface area is = 409.6 cm2.
The provided pyramid's surface area is equal to its square base plus its lateral sides.
The square base's area is given by (Side)2
= (8)2
= 64 cm2.
Area of the lateral side = 1/2 (Lateral height)(Base)
= √4² + (9.2)
2 [By applying Pythagoras theorem]
82.81+36
= √100.64
= 10.8 cm
Area of the lateral side = (8)(10.8)
= 86.4 cm²
The provided pyramid's surface area is calculated as follows:
Area of the base + 4(Area of one lateral side)
= 64 + 4(86.4)
= 409.6 cm2.
To learn more about surface area of pyramid from given link
https://brainly.com/question/23773586
#SPJ9
Solve for r 1+3r>10 please I need this solved aspap
Answers
The solution to the inequality 1 + 3r > 10 is r > 3.
This means that any value of r greater than 3 will satisfy the inequality.
To solve the inequality 1 + 3r > 10, we need to isolate the variable r on one side of the inequality sign.
Let's begin by subtracting 1 from both sides of the inequality:
1 + 3r - 1 > 10 - 1
This simplifies to:
3r > 9
Next, we can divide both sides of the inequality by 3 to solve for r:
(3r)/3 > 9/3
This simplifies to:
r > 3
For similar question on inequality.
https://brainly.com/question/30604125
#SPJ8
the functio f(x)=square root is translated using the rule (x,y) --> (x-6,y+9) to create A(x). which expression describes the range of A(x)?
Answers
Answer: Range is \(y \ge 9\)
Explanation:
The range of \(f(x) = \sqrt{x}\) is \(y \ge 0\)
In other words, it's the set of nonnegative real numbers.
We only focus on the y values. We go from y to y+9, which means we shift each (x,y) point 9 unit sup.
Since we shifted 9 units up, we add 9 to each y value and that effectively moves the lowest point in the range (0) up nine units.
So we go from \(y \ge 0\) to \(y \ge 9\)
If you need the range in interval notation, then you would write \([9, \infty)\). Note the square bracket next to the 9 so we include this as part of the range.
An item on sale costs 40% of the original price if the original price was $25 what is the sale price
Answers
Answer: $10
Step-by-step explanation:
original price = 25
40% = 0.4
25 * 0.4= 10
Your school’s track teams have been training hard for the entire season. There is a girls’ track team and a boys’ track team. The running times for each girl and boy were recorded after each race. You will use the results to help you answer questions about fractions and mixed numbers. Use what you know about adding and subtracting fractions and mixed numbers during the project.
Answers
4ln(3x)=-4
Solve for x

Answers
Answer:
4.4=-4
Step-by-step explanation:
just solving maths
Need help get it correct and get braì Liszt also need steps gl

Answers
According to the information, the volume of the three-dimensional rhombus is 61.92 cm³.
How to calculate the volume of the three-dimensional rhombus?The three-dimensional rhombus is a geometric solid in the shape of a prism whose lateral faces are rhombuses and the bases are parallelograms. To calculate its volume, the area of the base must be multiplied by the height of the prism.
In this case, the height of the prism is 3 cm and the dimensions of the base rhombus are 5.2 cm wide and 8 cm long. Since the rhombus has two diagonals of equal length, its area can be calculated using the formula (major diagonal x minor diagonal) / 2.
First, the length of the diagonals of the base rhombus must be calculated using the Pythagorean theorem, since its width and length are known:
major diagonal = √(5.2/2)^2 + 8^2 = √(13.04 + 64) = √77.04 = 8.78 cmminor diagonal = √(5.2/2)^2 + 3^2 = √(13.04 + 9) = √22.04 = 4.69 cmThen, the area of the base rhombus can be calculated:
area = (major diagonal x minor diagonal) / 2 = (8.78 cm x 4.69 cm) / 2 = 20.64 cm²Finally, the volume of the prism can be calculated:
volume = base area x height = 20.64 cm² x 3 cm = 61.92 cm³Therefore, the volume of the three-dimensional rhombus is 61.92 cm³.
Note: This question is incomplete. Here is the complete information:
Find the volume of the prism
Learn more about prisms in: https://brainly.com/question/29722724
#SPJ1
Triangle ABC has sides a>b>c. If one of the angles is 60 degrees, name the angle that can be equal to 90 degrees.
Answers
Answer:
angle b
Step-by-step explanation:
let's assume the triangle is a right angle triangle . either angle a or c can be equal to 60 degree
2. Heather made 35
cookies for a party. Ted
made 30 cookies. At
the party 47 cookies
were eaten. How many
cookies are left?
Answers
Answer:
18
Step-by-step explanation:
The total number of cookies that were made
35+30 = 65
The cookies that were eaten is 47
65-47 =18
There were 18 cookies left
Answer:
$18
Step-by-step explanation:
35+30=65
65-47=18
You are 22 years old and are starting a savings plan and will deposit $200 every 2 months until you retire. The account will give you 7% interest. How much do you expect your account to be worth when you retire at 67 years old?
Answers
Answer:
Formulae can be searched for confirmation : compounding interest with regular payments
Step-by-step explanation:
Calculations do it by yourself

Answer:
clchjtdjgdtklgdlnajajhbshsjzsnnjdndmqjsnsn him
What is the value of c?
a)4 units
b)5 units
c)6 units
d)7 units

Answers
The value of c in the triangle is (b) 5 units
Finding the value of c in the triangleFrom the question, we have the following parameters that can be used in our computation:
The right triangle
The length c is the hypotenuse of one of the triangles and can be calculated using the following Pythagoras theorem
c² = sum of squares of the legs
Using the above as a guide, we have the following:
c² = 3² + 4²
Evaluate
c² = 25
Take the square roots
c = 5
Hence, the hypotenuse of the right triangle is 5
Read more about right triangle at
https://brainly.com/question/2437195
#SPJ1
For each ordered pair (x, y), determine whether it is a solution to the inequality y≤0.
(8,-43)
(4.-22)
(-3,25)
(-7,45)
Is it a solution?
Answers
Answer:
(8,-43)
(4,-22)
Step-by-step explanation:
In order for the ordered pair to be a solution of the inequality, you must be able to plug in the y-value of the ordered pair and it must be less than or equal to 0.
For example:
(4,-22)
x=4 ; y=-22
Plug y into the inequality
y≤0
-22≤0
Since the statement is true, I know that (4,-22) must be a solution to the inequality.
Another way to solve this problem is by graphing. If an ordered pair is in the shaded region, it is a solution to the inequality. Attached is a graph of both the inequality and ordered pairs plotted.
If this answer helped you, please leave a thanks or a Brainliest!!!
Have a GREAT day!!!

Answer:
Step-by-step explanation:
To determine whether each ordered pair is a solution to the inequality y ≤ 0, we need to check if the y-coordinate of each pair is less than or equal to zero.
Let's check each ordered pair:
(8, -43):
The y-coordinate is -43. Since -43 is less than zero, this ordered pair is a solution to the inequality y ≤ 0.
(4, -22):
The y-coordinate is -22. Since -22 is less than zero, this ordered pair is a solution to the inequality y ≤ 0.
(-3, 25):
The y-coordinate is 25. Since 25 is greater than zero, this ordered pair is not a solution to the inequality y ≤ 0.
(-7, 45):
The y-coordinate is 45. Since 45 is greater than zero, this ordered pair is not a solution to the inequality y ≤ 0.
So, the solutions to the inequality y ≤ 0 are:
(8, -43) and (4, -22).
Help thank you! A B C or D

Answers
Answer:
below
Step-by-step explanation:
'x' cannot be zero because you would then have an illegal fraction with a zero denominator
the only interval listed that does not include zero is ( 1, +inf)
Answer:
D.
Step-by-step explanation:
f(x) = |x|
|x| = x for x > or = 0
|x| = -x for x < 0
At x = 0
Left limit = Right limit = Function value = 0
|x| = is continuous at x = 0.
Left derivative (at x = 0) = -1
Right derivative (at x = 0) = 1
Could someone please help here in so lost

Answers
Answer:
x=3
(26x+50degreese) = 134 degreese
Step-by-step explanation:
vector v has a horizontal vector component with magnitude 19 and a vertical vector component with magnitude 35. what is the acute angle theta formed by v and positive x-axis?
Answers
9514 1404 393
Answer:
61.5°
Step-by-step explanation:
The tangent relation is useful here. The angle is opposite the vertical side and adjacent to the horizontal side of the right triangle.
Tan = Opposite/Adjacent
tan(α) = 35/19
α = arctan(35/19) ≈ 61.5°
The angle made by v and the positive x-axis is 61.5°.
What is the center and radius of x^2+6x+y^2-4y =-4?
Answers
Answer:
The center of this circle is at \((-3,\, 2)\). The radius of this circle is \(3\).
Step-by-step explanation:
A circle with center \((a,\, b)\) and a radius of \(r\) (\(r > 0\)) could be expressed as:
\((x - a)^{2} + (y - b)^{2} = r^{2}\).
(In other words, a point is on this circle if and only if the distance between that point and the center is equal to the radius.)
Rearrange this equation using binomial expansion to match the equation given in this question:
\((x^{2} - 2\, a\, x + a^{2}) + (y^{2} - 2\, b\, y + b^{2}) = r^{2}\).
\(x^{2} + (-2\, a)\, x + y^{2} + (-2\, b)\, y = -a^{2} - b^{2} + r^{2}\).
The equation in this question is:
\(x^{2} + 6\, x + y^{2} + (-4)\, y = -4\).
Match up the coefficients of \(x\) and \(y\) in the two equations.:
Coefficient of \(x\): \((-2\, a) = 6\).Coefficient of \(y\): \((-2\, b) = (-4)\).Thus, \(a = (-3)\) and \(b = 2\).
The constants of the two equations should also match up:
\((-a^{2} - b^{2} + r^{2}) = (-4)\).
Substitute in \(a = (-3)\) as well as \(b = 2\) and solve for \(r\):
\(r^{2} = 9\).
\(r = 3\) (since \(r > 0\).)
Therefore, the center of this circle is \((-3,\, 2)\). The radius of this circle is \(3\).
Solve using tangent and cosine

Answers
The value of side length x in diagram a) is 4.3mm and side length x in diagram b) is 309.7 m.
What are the sides of the triangle labelled x?The figures in the image are right triangles.
A)
angle D = 17 degree
Adjacent to angle D = 14 mm
Opposite to angle D = x
To solve for the missing side length x, we use the trigonometric ratio.
Note that: tangent = opposite / adjacent
Hence:
tan( 17 ) = x/14
x = tan( 17 ) × 14
x = 4.3mm
B)
angle Z = 82 degree
Adjacent to angle Z = 43.1 m
Hypotenuse = x
Using trigonometric ratio,
cosine = adjacent / hypotenuse
cos( 82 ) = 43.1 / x
x = 43.1 / cos( 82 )
x = 309.7 m
Therefore, the measure of x is 309.7 meters.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
Help ASAP 6x - 3(2 – 3x)
Answers
Answer:
First: we expand
6x-(6-9x)
Then we simplify
6x-6+9x
Collect like terms
(6x+9x)-6
Simplify:
15x-6
The answer is 15x-6
Please help me the question

Answers
The polynomials completely factorized have the following expressions;
50). x³ - 3x² - 26x - 12 = (x - 6)(x + 1)(x + 2)
51). x³ - 12x² + 12x + 80 = (x - 10)(x + 2)(x - 4)
52). x³ - 18x² + 95x + 126 = (x - 9)(x - 2)(x - 7)
53). x³ - x² + 21x + 45 = (x + 5)(x - 3)(x - 3)
How to factorise the polynomials completelyFor the polynomial x³ - 3x² - 26x - 12 divisible by x - 6;
(x³ - 3x² - 26x - 12)/(x - 6) = x² + 3x + 2
x² + 3x + 2 = (x + 1)(x + 2)
so;
x³ - 3x² - 26x - 12 = (x - 6)(x + 1)(x + 2)
For the polynomial x³ - 12x² + 12x + 80 divisible by x - 10;
(x³ - 12x² + 12x + 80)/(x - 10) = x² - 2x - 8
x² - 2x - 8 = (x + 2)(x - 4)
so;
x³ - 12x² + 12x + 80 = (x - 10)(x + 2)(x - 4)
For the polynomial x³ - 18x² + 95x + 126 divisible by x - 9;
(x³ - 12x² + 12x + 80)/(x - 9) = x² - 9x + 14
x² - 9x + 14 = (x - 2)(x - 7)
so;
x³ - 18x² + 95x + 126 = (x - 9)(x - 2)(x - 7)
For the polynomial x³ - x² + 21x + 45 divisible by x + 5;
(x³ - x² + 21x + 45)/(x + 5) = x² - 6x + 9
x² - 6x + 9 = (x - 3)(x - 3)
so;
x³ - x² + 21x + 45 = (x + 5)(x - 3)(x - 3)
Therefore, by complete factorization the expressions (x - 6)(x + 1)(x + 2), (x - 10)(x + 2)(x - 4), (x - 9)(x - 2)(x - 7), and (x + 5)(x - 3)(x - 3) are the factors of their respective polynomial.
Read more about polynomial here:https://brainly.com/question/8021175
#SPJ1
Which equation represents a line that is parallel to the line y=3-2x
Answers
Answer:
any equation that include y = -2x
Step-by-step explanation:
if the equation has something like y = -2x + 4 or y = -5 - 2x is parallel
parallel lines have the same slope, the y intercept is not really important
Paulas cat weighs 8 5/8 pounds. Calebs cat weighs 11 1/8 pounds. What is the total weight of both cats?
Answers
Answer:
19 6/8 or 19 3/4
I’m not sure if you want the smallest possible fraction or not. If you don’t know just put the second one. K.
Carlos has 47 boxes that each have 10 markers. He gives 36 markers away.
How many markers does Carlos have left?
A. 93
B. 110
C. 434
D. 446
E. 506
Answers
which of these is the quadratic parent function

Answers
The quadratic parent function, f(x) = x², represents the most basic form of a quadratic function.
f(x) = x² is called the "parent" or "standard" form because it serves as a template or starting point for other quadratic functions.
In this function, x represents the input or independent variable, and f(x) represents the output or dependent variable.
The function takes any real number as an input, squares it, and produces the corresponding output.
By modifying the quadratic parent function with additional terms or coefficients, we can create different variations of quadratic functions that result in shifts, stretches, or compressions of the parabola, as well as changes in its orientation or vertex position.
To learn more on Functions click:
https://brainly.com/question/30721594
#SPJ1
Helppp the answer is $ pls

Answers
Answer:
$480
Step-by-step explanation:
Assuming that you have worked 10 hours and have done 3 policies in the equation 18h+100p, you want to plug in the said hours and policies into the variables to get this 18 (10) + 100 (3). You should get $480 as a result.
Andre draws a tape diagram for 3÷2/3
Andre says that 3÷2/3= 4 1/3 because there are 4 groups of 2/3 and 1/3 left. Do you agree with Andre? Explain your reasoning
Answers
Answer:
No I do not agree with Andre says that 3 divided by 2/3 Solving for 3 ÷ 2/3
3 ÷ 2/3
= 3 × 3/2
= 9/2
= 4 1/2
Therefore, 3 divided by 2/3 is 4 1/2
Andre's reasoning is wrong.
Step-by-step explanation:
It is incorrect
Let's divide and compare the sum
3 : 2/3 = 3*3/2 = 9/2 = 4 1/2
and
There are four 2/3 fractions and one 1/3 fraction
The 1/3 fraction is 1/2 of 2/3 fraction so instead of counting 1/3 as 1/3 it should be counted as 1/2