Consider this system of equations.
What is the solution to the system of equations?
2.1 + y = 11
2x - 5y = 8
Answers
Related Questions
(2x^2-9x-5) \div(x-5)
Answers
Answer:2x+1
Step-by-step explanation:
Find the
area of each
triangle.
9 m
5 m
8m

Answers
Answer:
22.5 \(m^{2}\)
Explanation:
The equation for the area of a triangle is \(\frac{1}{2}\)bh
In this case, the base is 9 m and the height is 5 m
9x5=45
45/2= 22.5
I'm working on a practice quiz can anyone help me with this

Answers
The lateral surface area of a cylinder is given by the expression:
\(\begin{gathered} LA=2\pi(radius)(height) \\ LA=2\pi(11)(9) \\ LA=622.035=622.04ft^2 \end{gathered}\)What is the least number by which 6750 maybe divided so that the quotient is a perfect cube
Answers
Answer:
2
Step-by-step explanation:
Definitions
Quotient: The result obtained by dividing one number by another.Perfect cube: The result obtained by multiplying the same integer three times.Prime number: a whole number greater than 1 that cannot be made by multiplying other whole numbers.Prime Factorization: prime numbers that multiply together to make the original number.Find the prime factorization of 6750
The first few prime numbers are: 2, 3, 5, 7, 11, 13, 17, ...
To find which prime numbers multiply together to make 6750, start by dividing 6750 by the first prime number, 2:
⇒ 6750 ÷ 2 = 3375
As 3375 is not a prime number, we need to divide again. 3375 is not divisible by 2, so let's try dividing it by the next prime number, 3:
⇒ 3375 ÷ 3 = 1125
Continue like this until the end result is a prime number:
⇒ 1125 ÷ 3 = 375
⇒ 375 ÷ 3 = 125
⇒ 125 ÷ 5 = 25
⇒ 25 ÷ 5 = 5
As 5 is a prime number, we can stop.
Therefore, 6750 is the product of:
⇒ 6750 = 2 × 3 × 3 × 3 × 5 × 5 × 5
As 3 and 5 appear three times, we can write this using exponents:
⇒ 6750 = 2 × 3³ × 5³
3³ and 5³ are perfect cubes. If they are multiplied together they make another perfect cube:
⇒ 3³ × 5³ = (3 × 5)³ = 15³
Therefore:
\(\sf \implies 6750=2 \times 15^3\)
\(\sf \implies \dfrac{6750}{2}=15^3\)
Therefore, the least number by which 6750 may be divided so that the quotient (result) is a perfect cube is 2.
Learn more about prime factorization here:
https://brainly.com/question/27804094
Hello,Can you please help me with question# 5 in the picture? thank you

Answers
Solution
\(a_1=9,for\text{ }n\ge2\)\(\begin{gathered} a_1=9 \\ a_2=\frac{2}{3a_{2-1}} \\ a_2=\frac{2}{3a_1} \\ a_2=\frac{2}{3(9)} \\ a_2=\frac{2}{27} \end{gathered}\)\(\begin{gathered} a_3=\frac{2}{3a_{3-1}} \\ a_3=\frac{2}{3a_2} \\ a_3=\frac{2}{3(\frac{2}{27})} \\ a_3=\frac{2}{\frac{2}{9}} \\ a_3=\frac{18}{2} \\ a_3=9 \end{gathered}\)\(\begin{gathered} a_4=\frac{2}{3a_3} \\ a_4=\frac{2}{3(9)} \\ a_4=\frac{2}{27} \end{gathered}\)Therefore for all values of n ≥ 2
\(a_1=9,a_2=\frac{2}{27},a_3=9,a_4=\frac{2}{27}\)
please help me answer this question thank you

Answers
Answer:
A
Step-by-step explanation:
Suppose that the relation S is defined as follows. S= {(4,9), (-9,4), (0, -9), (6, 6)} Give the domain and range of S. Write your answers using set notation.
domain =
range =
Answers
Given:
The relation S is:
\(S=\{(4,9),(-9,4),(0,-9),(6,6)\}\)
To find:
The domain and range of S.
Solution:
If a relation is defined by the set of ordered pairs (x,y), then the domain is the set of x-values and range is the set of y-values.
Let R be a relation defined as \(R=\{(x,y):x\in R,y\in R\}\), then \(Domain=\{x:x\in R\}\) and \(Range=\{y:y\in R\}\).
The given relation is:
\(S=\{(4,9),(-9,4),(0,-9),(6,6)\}\)
Here, x-values are 4,-9,0,6 and the y-values are 9,4,-9,6.
So, the domain and range of the given relation S are
\(Domain=\{-9,0,4,6\}\)
\(Range=\{-9,4,6,9\}\)
Therefore, \(Domain=\{-9,0,4,6\}\) and \(Range=\{-9,4,6,9\}\).
The graph of the equation x ^ 2 + y ^ 2 - 16x + 6y + 14 = 0 is a circle. An equivalent form of this equation is (x - 8) ^ 2 + (y + 3) ^ 2 = M
What is the value of M?
Answers
Answer:
author link
ghanami
Ace
2.9K answers
12.1M people helped
hello :
note :
an equation of the circle Center at the w(a,b) and ridus : r is :
(x-a)² +(y-b)² = r²
in this exercice : x²+y²-16x+6y+53=0
(x²-16x) +( y²+6y ) +53 = 0
(x² -2(8)x +8² - 8²) +(y² +2(3)x -3²+3² ) +53=0
(x² -2(8)x +8²) - 8² +(y² +2(3)x +3²)-3² +53=0
(x-8)² +( y+3)² = 20
the center is : w(8,-3) and ridus : r = √20
Still stuck? Get 1-on-1 help from an expert tutor now.
Step-by-step explanation:
Simplify the expression. Write your answer as a power.
(3.8^3)^4
The simplified expression is
Answers
(3.8^3)^4 = 9065737.91
Can you help with this question? I am kinda stuck.

Answers
Answer:
29400 cm²Step-by-step explanation:
The cube has 6 equal faces.
Total surface area:
S = 6a²S = 6*(0.7 m)² = 6*(70 cm) ² = 29400 cm²Let B be a 2 ×2 matrix such that
7B^2 −5B + 3I = 0.
Is B invertible? It so, what are the eigenvalues of B−1? Justify your answer.
Answers
Yes, Matrix B is invertible.
And, The eigenvalues of B−1 are;
⇒ (5 ± 7.68) / 14 - 1
What is mean by Matrix invertibility?An Invertible Matrix is a square matrix defined as invertible if the product of the matrix and its inverse is the identity matrix.
Given that;
B be a 2 ×2 matrix such that;
⇒ 7B² −5B + 3I = 0
Now,
Since, B be a 2 ×2 matrix.
And, The expression is,
⇒ 7B² −5B + 3I = 0
⇒ B² −5/7B + 3I/7 = 0
Multiply by B⁻¹, we get;
⇒ B - 5/7 + 3B⁻¹ = 0
Solve for B⁻¹;
⇒ 3B⁻¹ = - B + 5/7
⇒ B⁻¹ = - B/3 + 5/21
Thus, The matrix B is invertible.
And, The eigen value of B are;
⇒ 7B² −5B + 3I = 0
⇒ 7B² −5B + 3I = 0
⇒ B = - (-5) ± √(-5)² - 4×7×3 / 2×7
⇒ B = 5 ± √25 - 84/14
⇒ B = 5 ± √- 59 / 14
⇒ B = 5 ± 7.68 i / 14
⇒ B - 1 = (5 ± 7.68) / 14 - 1
Thus, Matrix B is invertible.
The eigenvalues of B−1 are = (5 ± 7.68) / 14 - 1
Learn more about the quadratic equation visit:
https://brainly.com/question/1214333
#SPJ1
PLEASE HELP ASAP I WILL GIVE YOU BRAINLIEST IF ANSWER IS CORRECT LOOK AT THE PICTURE

Answers
D 32
Because that’s what you get when you subtract 60
Please help me 4⅗ ÷ ⅕ =
Answers
Answer:
23
Step-by-step explanation:
just used a calculator
Let’s start by making the mixed number an improper fraction. To do this you multiply the whole number by the denominator and add the numerator.
4 x 5 + 3 = 23
No we have 23/5 divided by 1/5
We have common denominators but you don’t need them for multiplying and dividing fractions. To discuss fractions you just go across, but there’s a thing. You have to flip the second fraction then you can multiply instead of divide.
So
23/5 x 5/1
23 x 5 = 115
5 x 1 = 5
115/5
This can be simplified to 23 because 5 divided by 115 is 23.
Hope this helps
Find the area and the circumference of a circle with radius 7 m.
Use the value 3.14 for π, and do not round your answers.
Area=?
Circumference=?

Answers
Answer:
\(Area = 153.938040026m^2\)
\(Circumference= 43.9822971503m\)
Step-by-step explanation:
Area
\(Area = \pi r^2\\Area = \pi *7^2\\Area = 49\pi\\Area = 153.938040026\)
Circumference
\(C = 2\pi r\\C = 2\pi*7\\C= 14\pi\\C=43.9822971503\)
What are the numerical measures of each angle
in the diagram?
<1and <3 measure
degrees
<2 and <4 measure
degrees.
(3x - 1)
1
3
2
(2x + 9)

Answers
Answer:
angle 1 and 3 are equal by vertically opp. angle
3x-1 = 2x +9
3x-2x = 9+1
x = 10
put the value of x in any equation
3(10)-1 = 29
angle 1 = angle 3 = 29
angle 2 + angle 3 = 180 ° (linear pair)
angle 2 = 180 -29
angle 2 = 149
angle = angle 3 = 149.
Hope it helps
need help with this ASAP
!!!!!!!!!!!!!!!!!!!!!!!!

Answers
The fence in dead center is about 399 feet from the third base.
What is the Pythagorean Theorem?The Pythagorean Theorem states that in the case of a right triangle, the square of the length of the hypotenuse, which is the longest side, is equals to the sum of the squares of the lengths of the other two sides.
Hence the equation for the theorem is given as follows:
c² = a² + b².
In which:
c > a and c > b is the length of the hypotenuse.a and b are the lengths of the other two sides (the legs) of the right-angled triangle.For the triangle in this problem, we have that:
The sides are d ft and 90 ft.The hypotenuse is of 409 ft.Hence the distance is obtained as follows:
d² + 90² = 409²
\(d = \sqrt{409^2 - 90^2}\)
d = 399 ft.
More can be learned about the Pythagorean Theorem at brainly.com/question/30203256
#SPJ1
helppppppppppppppppp pleaseeeeeeee
A robot can complete 4 tasks in 10/3
hour. Each task takes the same amount of time.
a. How long does it take the robot to complete one task?
b. How many tasks can the robot complete in one hour?
Answers
Answer:
Robot will take hour to complete each task.
The robot can complete tasks in one hour.
Step-by-step explanation
We have been given that a robot can complete 8 tasks in 3/10 hour. Each task takes the same amount of time.
To find the time taken by robot to complete each task we will divide total time taken to complete 8 tasks by 8 as:
Now we will convert division problem into multiplication problem by flipping the 2nd fraction.
Therefore, robot will take hour to complete each task.
To find tasks completed by robot in one hour we will use proportions.
Therefore, the robot can complete tasks in one hour.
Look at image below for accurate information (type an integer or a decimal. Round to the nearest 10th as needed)

Answers
To solve this question we will use the formula for the volume of a cone and solve for h.
Recall that the volume of a cone is given by the following formula:
\(V=\frac{1}{3}hr^2\pi,\)where h is the height, and r is its radius.
Solving the above equation for h we get:
\(\begin{gathered} 3V=hr^2\pi, \\ h=\frac{3V}{r^2\pi}. \end{gathered}\)Substituting r=3.5 cm and V=63 cu cm we get:
\(h=\frac{3(63cm^3)}{(3.5cm)^2\pi}\approx4.9\operatorname{cm}.\)Answer: 4.9 cm.
Tom buys 4 tickets for a concert. The total cost is $85,60. How much does he pay
for each ticket?
Answers
Answer:
$21.40 for each ticket
Step-by-step explanation:
Answer:
$21.1
Step-by-step explanation:
classify the angles below as acute, right, obtuse or straight

Answers
Answer:
Obtuse - over 90°
Acute - less than 90°
Right - 90°
Straight - 180°
1. Obtuse
2. Acute
3. Right
2. Acute angel
3. Right angle
O
Which of the following could be used to calculate the area of the sector in the circle sho
O
m(Sin)
O
WE OD
m(Sin)2
O n(30in)2
O
r-5 in 30
m(30in)
O
above? (5 points)
Answers
The Circle Sector Area correct answer is: O n(30in)2
To calculate the area of the sector in the circle, you would typically use the formula:
Area = (θ/360) * π *\(r^2\)
where θ is the angle of the sector in degrees, π is a mathematical constant approximately equal to 3.14159, and r is the radius of the circle.
From the options you provided, the correct choice would be:
O n(30in)2
This option represents the square of the radius (30in) squared, which gives you the value of \(r^2.\)
Therefore, the Circle Sector Area correct answer is: O n(30in)2
For such more questions on Circle Sector Area
https://brainly.com/question/30607726
#SPJ8
Calculate the distance between the points P=(1, -1) and N=(5, -8) in the coordinate plane.
Round your answer to the nearest hundredth.
PLEASE PLEASE HELP ME

Answers
\(~~~~~~~~~~~~\textit{distance between 2 points} \\\\ P(\stackrel{x_1}{1}~,~\stackrel{y_1}{-1})\qquad N(\stackrel{x_2}{5}~,~\stackrel{y_2}{-8})\qquad \qquad d = \sqrt{( x_2- x_1)^2 + ( y_2- y_1)^2} \\\\\\ PN=\sqrt{(~~5 - 1~~)^2 + (~~-8 - (-1)~~)^2} \implies PN=\sqrt{(5 -1)^2 + (-8 +1)^2} \\\\\\ PN=\sqrt{( 4 )^2 + ( -7 )^2} \implies PN=\sqrt{ 16 + 49 } \implies PN=\sqrt{ 65 }\implies PN\approx 8.06\)
Determine the slope of the line that contains the points with coordinates (1, 5) and (-2, 7).
Answers
Answer:
2/3x
Step-by-step explanation:
What function is represented ?
A quartic function
An exponential function
A cubic function
A quadratic function
A linear function

Answers
Answer:
A cubic function
Step-by-step explanation:
I graphed it and connected the lines on desmos then compared to the types of calculus graphs on the search engine.
A garden is to designed with a rectangular part in the middle with two semi-circles on the ends.
The dimensions of the rectangular portion are 18.4 feet long and 8.6 feet wide.
a) What is the area of one semi-circle at one end?
b) What is the area of the garden?
c) Find the area in square metres.
Answers
Given statement solution is :- a) The area of one semi-circle at one end is 58.09 square feet.
b) The area of the garden is 274.42 square feet.
c) The area in square metres is approximately 58.09 square feet.
The area of the garden is approximately 274.42 square feet, and the area in square meters is approximately 25.49 square meters.
a) To find the area of one semi-circle at one end, we need to calculate the area of a complete circle and then divide it by 2. The formula for the area of a circle is A = πr², where A represents the area and r is the radius.
Since the diameter of the semi-circle is equal to the width of the rectangular portion, which is 8.6 feet, the radius will be half of that, which is 8.6 / 2 = 4.3 feet.
Now we can calculate the area of the semi-circle:
A = (π * 4.3²) / 2
A ≈ 58.09 square feet
b) To find the area of the garden, we need to sum the area of the rectangular portion with the areas of the two semi-circles.
Area of the rectangular portion = length * width
Area of the rectangular portion = 18.4 feet * 8.6 feet
Area of the rectangular portion ≈ 158.24 square feet
Area of the two semi-circles = 2 * (area of one semi-circle)
Area of the two semi-circles ≈ 2 * 58.09 square feet
Area of the two semi-circles ≈ 116.18 square feet
Total area of the garden = area of the rectangular portion + area of the two semi-circles
Total area of the garden ≈ 158.24 square feet + 116.18 square feet
Total area of the garden ≈ 274.42 square feet
c) To convert the area from square feet to square meters, we need to know the conversion factor. Since 1 foot is approximately 0.3048 meters, we can use this conversion factor to convert the area.
Area in square meters = Total area of the garden * (0.3048)²
Area in square meters ≈ 274.42 square feet * 0.3048²
Area in square meters ≈ 25.49 square meters
Therefore, the area of one semi-circle at one end is approximately 58.09 square feet. The area of the garden is approximately 274.42 square feet, and the area in square meters is approximately 25.49 square meters.
For such more questions on Garden Area Calculations
https://brainly.com/question/2516802
#SPJ8
One month Sam rented 3 movies and 5 video games for a total of $32. The next month, he rented 12 movies and 2 video games for a total of $29. Find the rental cost for a movie and a video game.
Answers
Using a system of equations, the rental cost for a movie and a video game is as follows:
Movie = $1.50Video game = $5.50.What is a system of equations?A system of equations is two or more equations solved concurrently or at the same time.
A system of equations is also described as simultaneous equations.
Movies Video Total
Games Cost
First month rental 3 5 $32
Second month rental 12 2 $29
Let the rental cost per movie = x
Let the rental cost per video game = y
Equations:
3x + 5y = 32 ... Equation 1
12x + 2y = 29 ... Equation 2
Multiply Equation 1 by 4:
12x + 20y = 128 ... Equation 3
Subtract Equation 2 from Equation 3:
12x + 20y = 128
-
12x + 2y = 29
18y = 99
y = 5.5
Substitute y = 5.5 in Equation 1 or 2:
12x + 2y = 29
12x + 2(5.5) = 29
12x + 11 = 29
12x = 18
x = 1.5
Thus, based on simultaneous equations, the rental cost for a movie is $1.50 while a video game's is $5.50.
Learn more about simultaneous equations at https://brainly.com/question/16863577.
#SPJ1
A tub has 50 small balls. Some balls are white, and summer orange. Without being able to see into the tub, each student in a class of 25 is allowed to pick a ball out of the tub at random. The color of the ball is recorded, and the ball is put back into the tub. At the end, seven orange balls and 18 white balls were picked. What is the best estimate you can give for the number of orange balls in the number of white balls in the tub? Describe how to calculate this best estimate, and explain why your method of calculation makes sense in a way that a seventh grader my understand. Is your best estimate necessarily accurate? Why or why not?
Answers
The best estimate we can give for the number of orange balls in the tub is 7, and the number of white balls in the tub is 43.
To calculate this, we take the number of orange balls picked (7) and divide it by the total number of balls picked (25) to get the proportion of orange balls in the tub. Then we multiply that proportion by the total number of balls in the tub (50) to get our estimate for the number of orange balls in the tub.
7 / 25 = 0.28
0.28 x 50 = 14
Similarly, we take the number of white balls picked (18) and divide it by the total number of balls picked (25) to get the proportion of white balls in the tub. Then we multiply that proportion by the total number of balls in the tub (50) to get our estimate for the number of white balls in the tub.
18 / 25 = 0.72
0.72 x 50 = 36
This method of calculation makes sense because it uses the data we have (the number of orange and white balls picked) to estimate the overall makeup of the tub. By using the proportion of orange and white balls picked, we can make an educated guess about how many of each color ball are in the tub without seeing it.
However, it's important to note that this best estimate is not necessarily accurate. The real number of orange and white balls in the tub could be different. The method used here is a probability method, it's best estimate based on the sample data. The sample data is based on a random selection of 25 balls, and the number of orange or white balls that would be picked could vary depending on the random draw. The more samples we take, the more accurate our estimate would be.
Someone help meeeeeeee
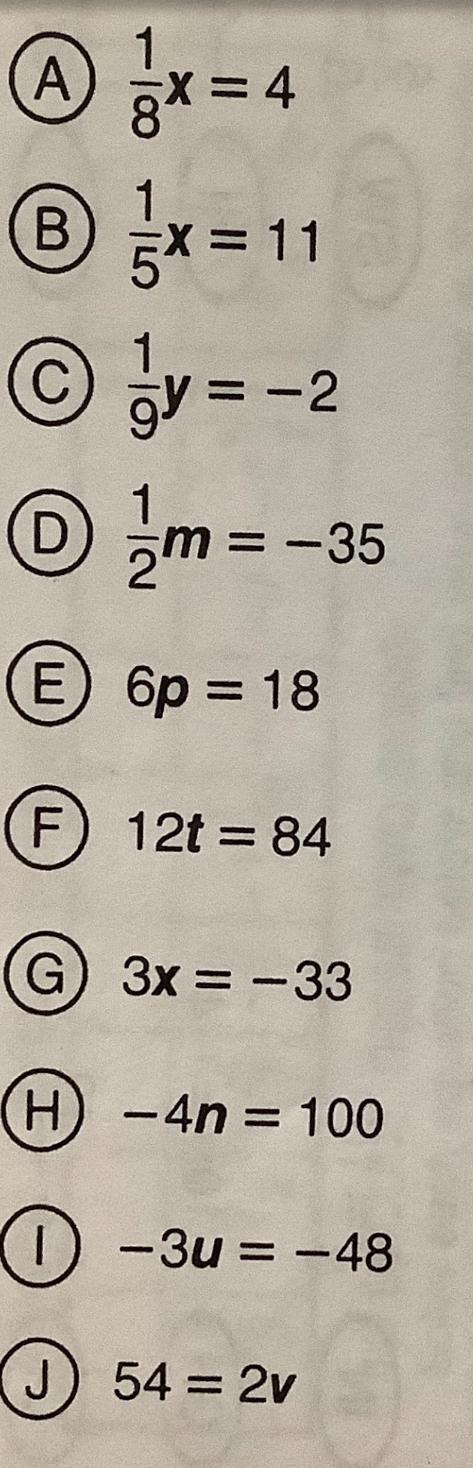
Answers
Answer:
A. x=32
B. x=55
C. y=-18
D. m=-70
E. p=3
F. t=7
G= x=-11
H. n=-25
I. u=16
J. v=27
Answer:
A) x = 32
B) x=55
C) y = -18
D) m = -70
E) p = 3
F) t = 7
G) x = -11
Step-by-step explanation:
\(A) \ \dfrac18x=4\implies x=4\times8\implies x=32\)
\(B) \ \dfrac15x=11\implies x=11\times5\implies x=55\)
\(C) \ \dfrac19y=-2\implies y=-2\times9\implies y=-18\)
\(D) \ \dfrac12m=-35\implies m=-35\times2\implies m=-70\)
\(E) \ 6p=18\implies p=\dfrac{18}6\implies p=3\)
\(F) \ 12t=84\implies t=\dfrac{84}{12}\implies t=7\)
\(G) \ 3x=-33\implies x=\dfrac{-33}3\implies x=-11\)
please someone
help me i’m stuck

Answers
Answer:
10 x \(5\frac{1}{3}\) x \(4\frac{1}{5}\) = 224
Step-by-step explanation:
It is B, hope this helps & please give me brainliest.
What is the value of x and y?

Answers
Answer:
x = 90y = 43Step-by-step explanation:
The angle bisector in this isosceles triangle is also its altitude. It meets the base segment at right angles.
x° = 90°
__
The acute angles in a right triangle are complementary.
y° = 90° -47°
y° = 43°